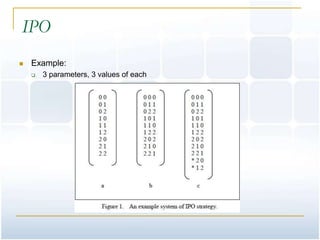
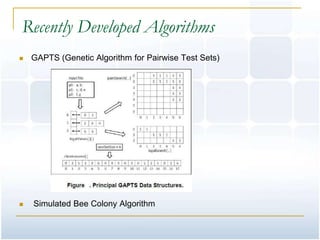
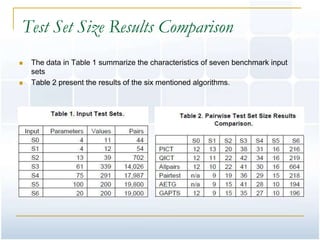
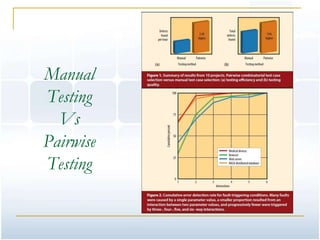
This document provides an overview of pairwise testing. It begins by defining pairwise testing and explaining that it aims to reduce the number of test cases needed while still covering all pairs of input parameters. It then outlines different methods for generating pairwise test cases, including orthogonal Latin squares, Automatic Efficient Test Generator (AETG), In-Parameter-Order (IPO), and genetic algorithms. The document compares the size of test sets generated by different algorithms and lists several pairwise testing tools. It concludes by mentioning additional references and resources on the topic of pairwise testing.

1. PAIRWISE TESTING
Sagar V. Hadawale
14 July, 2011

2. Agenda
 Introduction to Pairwise Testing
 Methods / Approaches / Algorithms
 Comparison
 Tools

3. Introduction to Pairwise Testing
 Pairwise testing is a combinatorial technique used to reduce the number
of test case inputs to a system in situations where exhaustive testing with
all possible inputs is not possible or prohibitively expensive.
 also known as 2-way testing, All-Pairs testing.
 most basic combinatorial method.
 for each pair of input parameters of a system, every combination of valid
values of these two parameters be covered by at least one test case.
 Exhaustive Testing Example:
 a manufacturing automation system that has 20 controls, each with 10
possible settings—a total of 1020 combinations, which is far more than a
software tester would be able to test in a lifetime.
 Surprisingly, we can check all pairs of these values with only 180 tests if they
are carefully constructed.

4. Pairwise Testing
 Example:
 3 parameters and 2 values
 OS: Windows, Linux
 CPU: Intel, AMD
 Protocol: IPv4, IPv6

5. Methods / Approaches / Algorithms
 Orthogonal Latin Squares / Orthogonal Array Testing
 Automatic Efficient Test Generator (AETG)
 In-Parameter-Order (IPO)
 Variant of In-Parameter-order (VIPO)
 Genetic Algorithm (GA)
 Recently Developed Algorithms

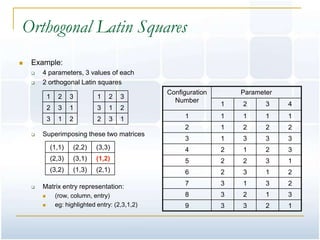
6. Orthogonal Latin Squares
 Latin Squares:
 Properties:
 no. of rows and columns must be equal
 each entry appears exactly once in each row and column
 A single n x n Latin square can handle three parameters, each of which
have n possible values.
 To handle more than three parameters, we need a set of orthogonal
Latin squares.
 If there are k system parameters, then k – 2 orthogonal Latin squares
are required.
 Orthogonal Latin Squares:
 Suppose we have two matrices [aij] and [bij]. The combined matrix is [cij]
where the elements are cij= (aij,bij). If cij ≠ crq whenever r ≠ i and q ≠ j, then the
squares [aij] and [bij] are orthogonal.

7. Orthogonal Latin Squares
 Example:
 4 parameters, 3 values of each
 2 orthogonal Latin squares
Configuration Parameter
1 2 3 1 2 3
Number
1 2 3 4
2 3 1 3 1 2
3 1 2 2 3 1 1 1 1 1 1
2 1 2 2 2
 Superimposing these two matrices
3 1 3 3 3
(1,1) (2,2) (3,3) 4 2 1 2 3
(2,3) (3,1) (1,2) 5 2 2 3 1
(3,2) (1,3) (2,1) 6 2 3 1 2
 Matrix entry representation: 7 3 1 3 2
 (row, column, entry) 8 3 2 1 3
 eg: highlighted entry: (2,3,1,2) 9 3 3 2 1

8. Orthogonal Latin Squares
 Limitations:
 For any n, there are at most n - 1 mutually orthogonal n x n Latin squares.
 If p is the smallest prime in the prime factorization of n, and occurs j times in
that factorization, then there exist at least pj -1 orthogonal Latin squares.
 Problematic case:
 when n = 4t + 2; for some integer t ≥ 1
 specially, t = 1
 one cannot find two 6 x 6 orthogonal Latin squares

9. Algebraic Strategy
 Special - case Algorithm:
 when N is prime number
 for (int n=0;n<N;n++) // counts the number test case for each variables
begin
for(int i=0;i<N;i++) // counts N test case for each n variables
begin
for (int j=0;j<N;j++) // fills the parameter values
begin
fill test case with ((n+(i*j))%N);
end
display and store the generated test set
end
end

10. Automatic Efficient Test Generator (AETG)
 Motivation:
 First, there are many systems where troublesome faults are caused by the
interaction of a few test parameters. A test plan should ideally cover those
interactions.
 Second is that the number of tests required to cover all n-way parameter
combinations, for fixed n, grows logarithmically in the number of parameters.
 Approach:
 generate a test set for the first two parameters, and then iteratively extend
the test set to account for each remaining parameter.
 A Heuristic Algorithm:
 The proof of logarithmic growth for the greedy algorithm assumes that at
each stage it is possible to find a test case that covers the maximum number
of uncovered pairs. Since there can be many possible test cases, it is not
always computationally possible to find an optimal test case.

11. In-Parameter-Order (IPO)
 Strategy:
 problem of generating minimum pairwise test sets is NP-complete
 For a system with two or more input parameters, the IPO strategy generates
a pairwise test set for the first two parameters, extends the test set to
generate a pairwise test set for the first three parameters, and continues to
do so for each additional parameter.
 The extension of a test set for the addition of a new parameter includes the
following two steps:
 (a) horizontal growth, which extends each existing test by adding one value of the
new parameter, and values are chosen in a greedy manner.
 (b) vertical growth, which adds new tests, if necessary, after the completion of
horizontal growth.

12. IPO
 Framework:
 Assume that system S has parameters p1,p2,.. and pn and n ≥ 2
Strategy In-Parameter-Order
begin
{for the first two parameters p1 and p2}
T = {(v1, v2) | v1 and v2 are values of p1 and p2 respectively}
if n = 2 then stop;
{for the remaining parameters}
for parameter pi, i = 3, 4,….., n do
begin
{horizontal growth}
for each test (v1, v2, …. , vi-1) in T do
replace it with (v1, v2, … , vi-1, vi),
where vi is a value of pi;
{vertical growth}
while T does not cover all pairs between pi and each of p1, p2, … , pi -1 do
add a new test for p1, p2, … , pi to T;
end
end

13. IPO
 Example:
 3 parameters, 3 values of each

14. Variant of In-Parameter-order (VIPO)
 shares the same framework as IPO
 uses different heuristics for the greedy construction of each test case
 Example:
 3 parameters, 3 values of each

15. Genetic Algorithm (GA)
 generate the configuration sets and based on fitness of each set to
select a set that can serve as S (set of test configurations)
 2 main parts
 Chromosome structure:
 each chromosome C (a subset of T), consists of a number of configurations, where
T is the set of all possible test configurations.
 form: {v1, … , vn} having one value for each parameter
 Fitness function:
 number of distinct pair-wise interaction configurations covered by all
of the chromosome’s configurations
=
the total number of possible pair-wise interaction configurations, |Φ2|

16. Genetic Algorithm (GA)
 Fitness function:
 Example:
 chromosome having two configurations for three parameters: {{1,2,2}, {1,1,2}}
 suppose each of the parameters can take two possible values, namely 1 or 2.
 set of pair-wise interaction configurations covered by the chromosome in hand:
N1 = {{1, 2, X}, {1, X, 2}, {X, 2, 2}}
N2 = {{1, 1, X}, {1, X, 2}, {X, 1, 2}}
Here, Ni is the set of distinct pair-wise interaction elements covered by
configuration i.
 so, overall number of distinct pair-wise configurations covered by the chromosome
= 3+3-1=5
 Φ2 = {{1, 1, X}, {1, 2, X}, {2, 1, X}, {2, 2, X}, {1, X, 1}, {1, X, 2}, {2, X, 1}, {2, X, 2},
{X, 1, 1}, {X, 1, 2}, {X, 2, 1}, {X, 2, 2}} and
| Φ2 | = 12
 Fitness = 5 / 12 = 0.42

17. Recently Developed Algorithms
 GAPTS (Genetic Algorithm for Pairwise Test Sets)
 Simulated Bee Colony Algorithm

18. Test Set Size Results Comparison
 The data in Table 1 summarize the characteristics of seven benchmark input
sets
 Table 2 present the results of the six mentioned algorithms.

19. Manual
Testing
Vs
Pairwise
Testing

20. Tools
 AETG
 IPO
 Tconfig
 CTS
 Jenny
 TestCover
 DDA
 AllPairs
 PICT
 EXACT
 IPO-s
 Hexawise

21. References
1) A. W. Williams, R. L. Probert, "A Practical Strategy for Testing Pair-wise Coverage of Network Interfaces",
Software Reliability Engineering, 1996. Proceedings., Seventh International Symposium on, 1996 , pp. 246 - 254
2) D. M. Cohen, S. R. Dalal, M. L. Fredman, G. C. Patton, ―The AETG system: An Approach to Testing Based on
Combinatorial Design‖, IEEE Transaction on Software Engineering, 23 (7), 1997, pp. 437-443.
3) J. D. McCaffrey, "An Empirical Study of Pairwise Test Set Generation Using a Genetic Algorithm", ITNG, 2010
Seventh International Conference on, 2010 , pp. 992 - 997
4) J. D. McCaffrey, "Generation of Pairwise Test Sets using a Genetic Algorithm", Computer Software and
Applications Conference, 2009. COMPSAC '09. 33rd Annual IEEE International, 2009, pp. 626 - 631
5) J. D. McCaffrey, "Generation of Pairwise Test Sets using a Simulated Bee Colony Algorithm", Information Reuse &
Integration, 2009. IRI '09. IEEE International Conference on, 2009, pp. 115 - 119
6) M. I. Younis, K. Z. Zamli, N. A. M. Isa, "Algebraic strategy to generate pairwise test set for prime number
parameters and variables" Information Technology, 2008. ITSim 2008. International Symposium on, Volume: 3,
2008, pp. 1 - 4
7) R. Kuhn, R. Kacker, Yu Lei, J. Hunter, "Combinatorial Software Testing", Computer, Volume: 42 , Issue: 8, 2009 ,
pp. 94 - 96
8) R. Kuhn, R. Kacker, Yu Lei, "Practical Combinatorial Testing- Beyond Pairwise" IT Professional, Volume: 10 ,
Issue: 3, 2008 , pp. 19 - 23
9) S.A. Ghazi and M.A. Ahmed, "Pair-wise Test Coverage Using Genetic Algorithms", Proceedings of the 2003
Congress on Evolutionary Computation, vol. 2, December 2003, pp. 1420-1424.
10) Yingxia Cui, Longshu Li, Sheng Yao, "A New Strategy for Pairwise Test Case Generation", Intelligent Information
Technology Application, 2009. IITA 2009. Third International Symposium on Volume: 3, 2009 , pp. 303 - 306
11) Yu Lei and K.C. Tai, "In-Parameter-Order: A Test Generation Strategy for Pairwise Testing", Proceedings of Third
IEEE International High-Assurance Systems Engineering Symposium, Nov. 1998, pp. 254-261.

22. Other Useful Resources
 http://www.pairwise.org/default.html
 http://www.developsense.com/pairwiseTesting.html
 http://www.softwaretestingstuff.com/2007/10/pairwise-testing.html
 Hexawise Testing:
 website: http://hexawise.com/
 videos:
 http://www.youtube.com/watch?v=hlFh718i0VQ
 Hexawise amazon example: 9 parts
 2nd part link: http://www.youtube.com/watch?v=BFjDqAnMcew

23. Any Questions?