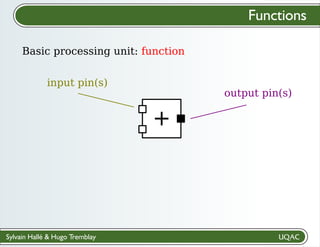
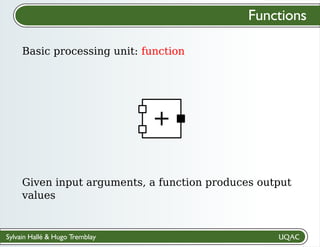
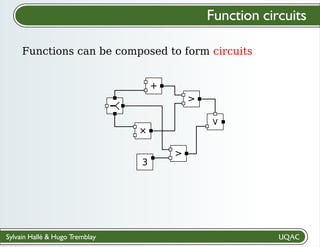
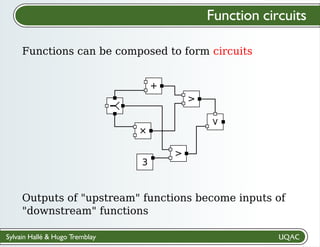
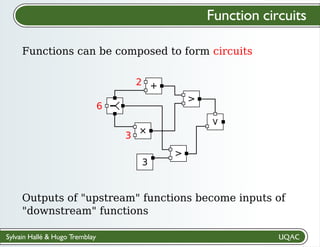
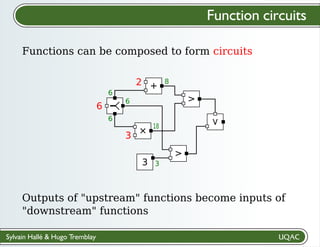
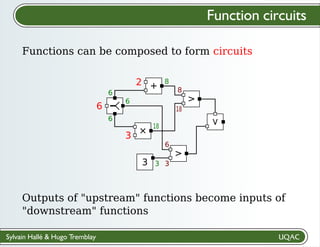
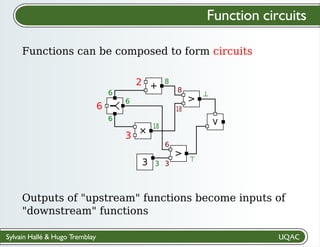
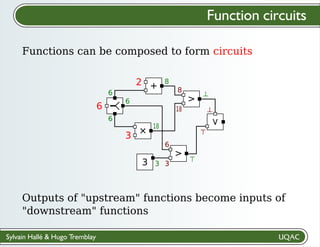
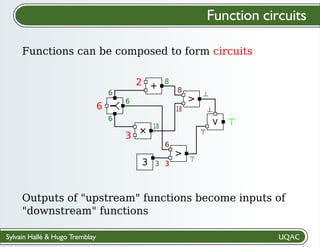
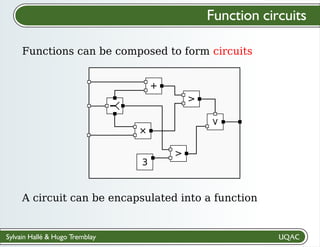
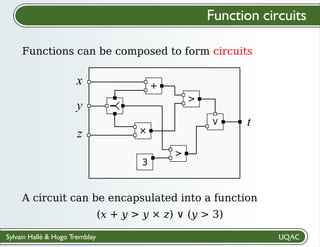
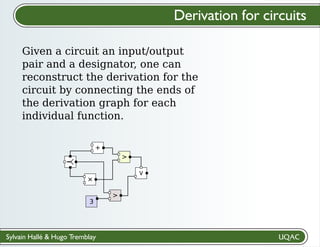
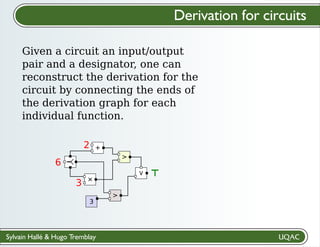
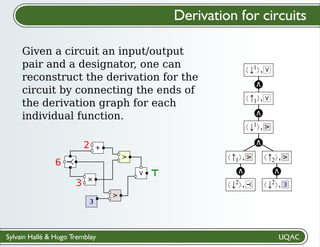
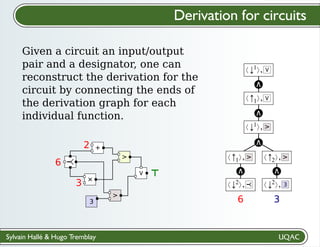
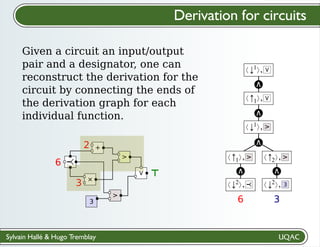
The document describes a framework for explaining the output of function circuits. It introduces the concept of functions as basic processing units that take inputs and produce outputs. Functions can be composed into circuits where the output of one function is the input of another. The framework represents circuits using designation graphs that trace the propagation of values between function inputs and outputs. It defines derivation operators that take a designation graph and reconstruct the derivation of an output value from input values through the functions in the circuit. This allows explaining how a circuit produced a particular output from its inputs.


![Sylvain Hallé & Hugo Tremblay
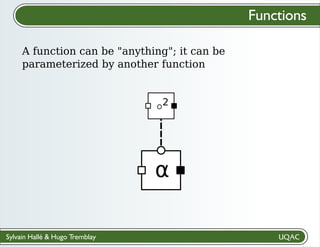
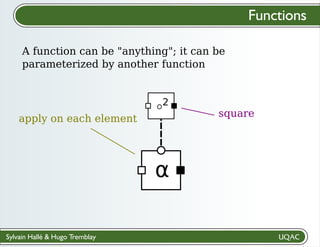
A function can be "anything"; it can be
parameterized by another function
Functions
α
2
[4,2,5] [16,4,25]](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-8-320.jpg)
![Sylvain Hallé & Hugo Tremblay
α
>
3
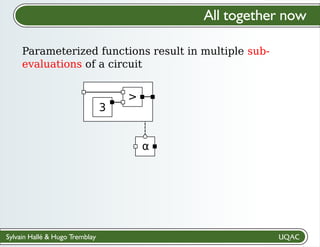
Parameterized functions result in multiple sub-
evaluations of a circuit
All together now
[4,2,5]](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-20-320.jpg)
![Sylvain Hallé & Hugo Tremblay
α
>
3
Parameterized functions result in multiple sub-
evaluations of a circuit
All together now
[4,2,5]
>
3
4
44
3
T
T3
T[ ]](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-21-320.jpg)
![Sylvain Hallé & Hugo Tremblay
α
>
3
Parameterized functions result in multiple sub-
evaluations of a circuit
All together now
[4,2,5]
>
3
4
44
3
T
T3
T[ ]
>
3
2
2
3
T
T
3
T](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-22-320.jpg)
![Sylvain Hallé & Hugo Tremblay
α
>
3
Parameterized functions result in multiple sub-
evaluations of a circuit
All together now
[4,2,5]
>
3
4
44
3
T
T3
T[ ]
>
3
2
2
3
T
T
3
T
>
3
5
5
3
T
T3
T](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-23-320.jpg)




![Sylvain Hallé & Hugo Tremblay
A designator is any function that takes an object
and returns a part of this object. Examples:
Designator
[i] the i-th item of a list
[i : j] the substring between characters i and j
the contents of some file
the i-th input pin of a function
the i-th output pin of a function
↑i
↓i](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-31-320.jpg)
![Sylvain Hallé & Hugo Tremblay
Designators can be composed:
↑2 [3] [1:5]◦ ◦
A designator is any function that takes an object
and returns a part of this object. Examples:
Designator
[i] the i-th item of a list
[i : j] the substring between characters i and j
the contents of some file
the i-th input pin of a function
the i-th output pin of a function
↑i
↓i](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-32-320.jpg)
![Sylvain Hallé & Hugo Tremblay
Designators can be composed:
↑2 [3] [1:5]◦ ◦
"The first five characters of the third
item of the second argument of the
function"
A designator is any function that takes an object
and returns a part of this object. Examples:
Designator
[i] the i-th item of a list
[i : j] the substring between characters i and j
the contents of some file
the i-th input pin of a function
the i-th output pin of a function
↑i
↓i](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-33-320.jpg)
![Sylvain Hallé & Hugo Tremblay
Designation graph
∧
↓ , f1
< <
↑ , f1< <
∧
[1],↑ , f2< < [1],↑ , f3< <
A designation graph is an and-or directed acyclic
graph (DAG) where:
the endpoints are made of a designator d and a
function f
the head of d points to an input or an output of f
It expresses an "and-or"
relationship between
function inputs and
function outputs in a
circuit.](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-34-320.jpg)



![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-43-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
split file
into lines](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-44-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
on each
line...](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-45-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
split on
commas](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-46-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
take
second
element](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-47-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
convert to
number](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-48-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
on each
window of
3 values...](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-49-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
take the
average](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-50-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
on each
average...](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-51-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
check that is
is greater than 3](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-52-320.jpg)
![Sylvain Hallé & Hugo Tremblay
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example
assert they
are all so](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-53-320.jpg)
![Sylvain Hallé & Hugo Tremblay
⊤the,2,penny
fool,7,lane
on,18,come
the,2,together
hill,-80,i
strawberry,7,am
fields,1,the
forever,10,walrus
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-54-320.jpg)
![Sylvain Hallé & Hugo Tremblay
⊤the,2,penny
fool,7,lane
on,18,come
the,2,together
hill,-80,i
strawberry,7,am
fields,1,the
forever,10,walrus
∧
↓ , G1< <
∧ ∧∧
[4:5], [3] ,< < [5:5], [4] ,< < [6:8], [5] ,< < [8:8], [7] ,< <[ : ], [6] ,< <12 12
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-55-320.jpg)
![Sylvain Hallé & Hugo Tremblay
⊤the,2,penny
fool,7,lane
on,18,come
the,2,together
hill,-80,i
strawberry,7,am
fields,1,the
forever,10,walrus
∧
↓ , G1< <
∧ ∧∧
[4:5], [3] ,< < [5:5], [4] ,< < [6:8], [5] ,< < [8:8], [7] ,< <[ : ], [6] ,< <12 12
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-56-320.jpg)
![Sylvain Hallé & Hugo Tremblay
⊤the,2,penny
fool,7,lane
on,18,come
the,2,together
hill,-80,i
strawberry,7,am
fields,1,the
forever,10,walrus
∧
↓ , G1< <
∧ ∧∧
[4:5], [3] ,< < [5:5], [4] ,< < [6:8], [5] ,< < [8:8], [7] ,< <[ : ], [6] ,< <12 12
∧
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-57-320.jpg)
![Sylvain Hallé & Hugo Tremblay
⊤the,2,penny
fool,7,lane
on,18,come
the,2,together
hill,-80,i
strawberry,7,am
fields,1,the
forever,10,walrus
∧
↓ , G1< <
∧ ∧∧
[4:5], [3] ,< < [5:5], [4] ,< < [6:8], [5] ,< < [8:8], [7] ,< <[ : ], [6] ,< <12 12
∧
/, [2] #
α W
3
x
Gα
>
3
1 2
A
C
3 4
B
5
a b c
a
b
A bigger example](https://image.slidesharecdn.com/slides-200622132524/85/A-Generic-Explainability-Framework-for-Function-Circuits-58-320.jpg)

