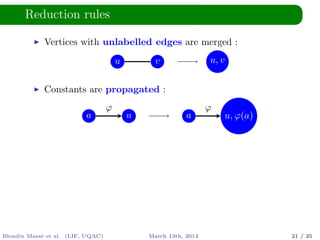
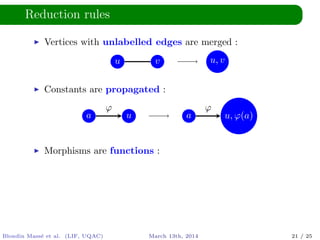
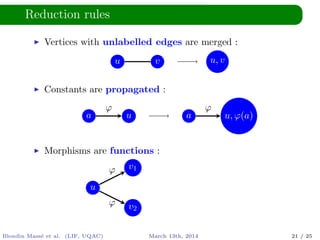
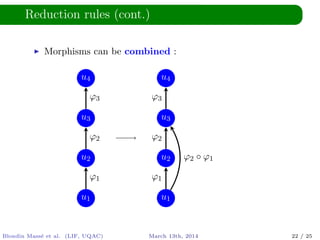
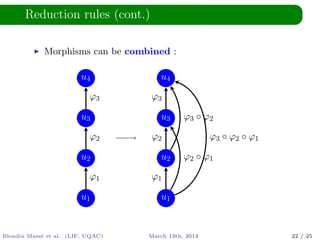
The document discusses solving equations based on words, utilizing morphisms and antimorphisms within the context of language and automata theory. It introduces concepts like distinct squares conjecture, symbolic expressions, and ways assignments extend to different expressions. The authors highlight the decidability of the problem and mention existing tools that address string constraints but do not handle morphisms and antimorphisms.

1. Solving Equations on Words with Morphisms
and Antimorphisms
A. Blondin Mass´e, S. Gaboury, S. Hall´e and M. Larouche
Laboratoire d’informatique formelle
Universit´e du Qu´ebec `a Chicoutimi
Chicoutimi, Canada
Language and Automata Theory and Applications
(LATA 2014)
March 13th, 2014
Madrid, Spain
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 1 / 25

2. Outline
1. Introduction
2. Words equations
3. From equations to graphs
4. Conclusion
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 2 / 25

3. Outline
1. Introduction
2. Words equations
3. From equations to graphs
4. Conclusion
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 3 / 25

4. Distinct squares conjecture
Conjecture (Fraenkel and Simpson, 1998)
A word of length n contains less than n distinct squares.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 4 / 25

5. Distinct squares conjecture
Conjecture (Fraenkel and Simpson, 1998)
A word of length n contains less than n distinct squares.
The 8 squares of the word w = 0000110110101 of length
13 are
00, 11, 0000, 0101, 1010, 011011, 101101, 110110.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 4 / 25

6. Distinct squares conjecture
Conjecture (Fraenkel and Simpson, 1998)
A word of length n contains less than n distinct squares.
The 8 squares of the word w = 0000110110101 of length
13 are
00, 11, 0000, 0101, 1010, 011011, 101101, 110110.
We look at the solutions of the equations
x1u2
1y1 = x2u2
2y2 = . . . = xku2
kyk,
with various lenghts of the xi’s and the ui’s.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 4 / 25

7. Tilings
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 5 / 25

8. Tilings
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 5 / 25

9. Tilings
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 5 / 25

10. Tilings
On the Freeman chain code F = {0, 1, 2, 3} :
(xyˆxˆy)2
= pztˆzˆts,
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 5 / 25

11. Tilings
On the Freeman chain code F = {0, 1, 2, 3} :
(xyˆxˆy)2
= pztˆzˆts,
It is easier to solve the equation on the turns alphabet
{R, L, F} :
(xLyLˆxLˆyL)2
= uzLtLˆzLˆtLv.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 5 / 25

12. Solving equations on words
Makanin showed that the problem of solving equations on
words with constants and variables is decidable
(1977) ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 6 / 25

13. Solving equations on words
Makanin showed that the problem of solving equations on
words with constants and variables is decidable
(1977) ;
Plandowski showed that the problem is in fact in
PSPACE (1999) ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 6 / 25

14. Solving equations on words
Makanin showed that the problem of solving equations on
words with constants and variables is decidable
(1977) ;
Plandowski showed that the problem is in fact in
PSPACE (1999) ;
Abdulrab propose a Lisp implementation of a solver in
1990 (not available anymore) ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 6 / 25

15. Solving equations on words
Makanin showed that the problem of solving equations on
words with constants and variables is decidable
(1977) ;
Plandowski showed that the problem is in fact in
PSPACE (1999) ;
Abdulrab propose a Lisp implementation of a solver in
1990 (not available anymore) ;
More recenly, tools such as Hampi, Omega and Stranger
deal with string constraints and regular expressions ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 6 / 25

16. Solving equations on words
Makanin showed that the problem of solving equations on
words with constants and variables is decidable
(1977) ;
Plandowski showed that the problem is in fact in
PSPACE (1999) ;
Abdulrab propose a Lisp implementation of a solver in
1990 (not available anymore) ;
More recenly, tools such as Hampi, Omega and Stranger
deal with string constraints and regular expressions ;
None handles morphisms and antimorphisms.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 6 / 25

17. Outline
1. Introduction
2. Words equations
3. From equations to graphs
4. Conclusion
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 7 / 25

18. Basics
Alphabet Σ, free monoid Σ∗, ε is the empty word ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 8 / 25

19. Basics
Alphabet Σ, free monoid Σ∗, ε is the empty word ;
A morphism is a map ϕ : Σ∗ → Σ∗ such that
ϕ(uv) = ϕ(u)ϕ(v) ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 8 / 25

20. Basics
Alphabet Σ, free monoid Σ∗, ε is the empty word ;
A morphism is a map ϕ : Σ∗ → Σ∗ such that
ϕ(uv) = ϕ(u)ϕ(v) ;
An antimorphism is a map ϕ : Σ∗ → σ∗ such that
ϕ(uv) = ϕ(v)ϕ(u)
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 8 / 25

21. Basics
Alphabet Σ, free monoid Σ∗, ε is the empty word ;
A morphism is a map ϕ : Σ∗ → Σ∗ such that
ϕ(uv) = ϕ(u)ϕ(v) ;
An antimorphism is a map ϕ : Σ∗ → σ∗ such that
ϕ(uv) = ϕ(v)ϕ(u)
Morphism and antimorphisms are completely determined
by their action on single letters ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 8 / 25

22. Basics
Alphabet Σ, free monoid Σ∗, ε is the empty word ;
A morphism is a map ϕ : Σ∗ → Σ∗ such that
ϕ(uv) = ϕ(u)ϕ(v) ;
An antimorphism is a map ϕ : Σ∗ → σ∗ such that
ϕ(uv) = ϕ(v)ϕ(u)
Morphism and antimorphisms are completely determined
by their action on single letters ;
If ϕ is an antimorphism, then ϕ = · · ϕ , where ϕ is a
morphism ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 8 / 25

23. Basics
Alphabet Σ, free monoid Σ∗, ε is the empty word ;
A morphism is a map ϕ : Σ∗ → Σ∗ such that
ϕ(uv) = ϕ(u)ϕ(v) ;
An antimorphism is a map ϕ : Σ∗ → σ∗ such that
ϕ(uv) = ϕ(v)ϕ(u)
Morphism and antimorphisms are completely determined
by their action on single letters ;
If ϕ is an antimorphism, then ϕ = · · ϕ , where ϕ is a
morphism ;
A morphism (or antimorphism) is called k-uniform if
ϕ(a) = k for every a ∈ Σ ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 8 / 25

24. Basics
Alphabet Σ, free monoid Σ∗, ε is the empty word ;
A morphism is a map ϕ : Σ∗ → Σ∗ such that
ϕ(uv) = ϕ(u)ϕ(v) ;
An antimorphism is a map ϕ : Σ∗ → σ∗ such that
ϕ(uv) = ϕ(v)ϕ(u)
Morphism and antimorphisms are completely determined
by their action on single letters ;
If ϕ is an antimorphism, then ϕ = · · ϕ , where ϕ is a
morphism ;
A morphism (or antimorphism) is called k-uniform if
ϕ(a) = k for every a ∈ Σ ;
We then write |ϕ| = k.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 8 / 25

25. Words equations systems
Systems of words equations are represented by
Σ the set of constants ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 9 / 25

26. Words equations systems
Systems of words equations are represented by
Σ the set of constants ;
V the set of variables ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 9 / 25

27. Words equations systems
Systems of words equations are represented by
Σ the set of constants ;
V the set of variables ;
M the set of morphisms ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 9 / 25

28. Words equations systems
Systems of words equations are represented by
Σ the set of constants ;
V the set of variables ;
M the set of morphisms ;
A the set of antimorphisms ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 9 / 25

29. Words equations systems
Systems of words equations are represented by
Σ the set of constants ;
V the set of variables ;
M the set of morphisms ;
A the set of antimorphisms ;
a list of words equations Li = Ri (i = 1, 2, . . . , m).
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 9 / 25

30. Symbolic expressions
A symbolic expression (or simply expression) is either
ε, a constant, or a variable ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 10 / 25

31. Symbolic expressions
A symbolic expression (or simply expression) is either
ε, a constant, or a variable ;
v1v2 · · · vk, where vi is itself an expression ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 10 / 25

32. Symbolic expressions
A symbolic expression (or simply expression) is either
ε, a constant, or a variable ;
v1v2 · · · vk, where vi is itself an expression ;
ϕ(v), where v is an expression and ϕ ∈ M ∪ A ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 10 / 25

33. Example
Take
Σ = {a, b};
V = {x, y};
M = {ϕ}, ϕ : a → b, b → a;
A = { · }
Then
abxy = ϕ(x)yab
is a word equation.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 11 / 25

34. Assignments and solutions
An assignment is a map I : V → Σ∗ ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 12 / 25

35. Assignments and solutions
An assignment is a map I : V → Σ∗ ;
Is is naturally extended as follows
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 12 / 25

36. Assignments and solutions
An assignment is a map I : V → Σ∗ ;
Is is naturally extended as follows
1. I(ε) = ε ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 12 / 25

37. Assignments and solutions
An assignment is a map I : V → Σ∗ ;
Is is naturally extended as follows
1. I(ε) = ε ;
2. I(u) = u, for u ∈ Σ ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 12 / 25

38. Assignments and solutions
An assignment is a map I : V → Σ∗ ;
Is is naturally extended as follows
1. I(ε) = ε ;
2. I(u) = u, for u ∈ Σ ;
3. I(u1 · u2 · · · uk) = I(u1) · I(u2) · · · I(uk), if ui is an
expression (i = 1, 2, . . . , k) ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 12 / 25

39. Assignments and solutions
An assignment is a map I : V → Σ∗ ;
Is is naturally extended as follows
1. I(ε) = ε ;
2. I(u) = u, for u ∈ Σ ;
3. I(u1 · u2 · · · uk) = I(u1) · I(u2) · · · I(uk), if ui is an
expression (i = 1, 2, . . . , k) ;
4. I(ϕ(u)) = ϕ(I(u)), if ϕ ∈ M ∪ A and u is an
expression.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 12 / 25

40. Assignments and solutions
An assignment is a map I : V → Σ∗ ;
Is is naturally extended as follows
1. I(ε) = ε ;
2. I(u) = u, for u ∈ Σ ;
3. I(u1 · u2 · · · uk) = I(u1) · I(u2) · · · I(uk), if ui is an
expression (i = 1, 2, . . . , k) ;
4. I(ϕ(u)) = ϕ(I(u)), if ϕ ∈ M ∪ A and u is an
expression.
Let L = R be an equation ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 12 / 25

41. Assignments and solutions
An assignment is a map I : V → Σ∗ ;
Is is naturally extended as follows
1. I(ε) = ε ;
2. I(u) = u, for u ∈ Σ ;
3. I(u1 · u2 · · · uk) = I(u1) · I(u2) · · · I(uk), if ui is an
expression (i = 1, 2, . . . , k) ;
4. I(ϕ(u)) = ϕ(I(u)), if ϕ ∈ M ∪ A and u is an
expression.
Let L = R be an equation ;
A solution of L = R is an assigment S : V → Σ∗such that
S(L) = S(R).
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 12 / 25

42. Bounded lengths
Since solving general equations on words is very hard, we
need to restrict the context ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 13 / 25

43. Bounded lengths
Since solving general equations on words is very hard, we
need to restrict the context ;
To simplify, we assume that all lenghts of variables are
known ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 13 / 25

44. Bounded lengths
Since solving general equations on words is very hard, we
need to restrict the context ;
To simplify, we assume that all lenghts of variables are
known ;
Let λ : V → N, where λ(v) is the length of the variable v ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 13 / 25

45. Bounded lengths
Since solving general equations on words is very hard, we
need to restrict the context ;
To simplify, we assume that all lenghts of variables are
known ;
Let λ : V → N, where λ(v) is the length of the variable v ;
Naturally,
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 13 / 25

46. Bounded lengths
Since solving general equations on words is very hard, we
need to restrict the context ;
To simplify, we assume that all lenghts of variables are
known ;
Let λ : V → N, where λ(v) is the length of the variable v ;
Naturally,
1. λ(ε) = 0 ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 13 / 25

47. Bounded lengths
Since solving general equations on words is very hard, we
need to restrict the context ;
To simplify, we assume that all lenghts of variables are
known ;
Let λ : V → N, where λ(v) is the length of the variable v ;
Naturally,
1. λ(ε) = 0 ;
2. λ(u) = 1 for u ∈ Σ ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 13 / 25

48. Bounded lengths
Since solving general equations on words is very hard, we
need to restrict the context ;
To simplify, we assume that all lenghts of variables are
known ;
Let λ : V → N, where λ(v) is the length of the variable v ;
Naturally,
1. λ(ε) = 0 ;
2. λ(u) = 1 for u ∈ Σ ;
3. λ(u1 · u2 · · · uk) = k
i=1 λ(ui), if ui is an expression for
i = 1, 2, . . . , k ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 13 / 25

49. Bounded lengths
Since solving general equations on words is very hard, we
need to restrict the context ;
To simplify, we assume that all lenghts of variables are
known ;
Let λ : V → N, where λ(v) is the length of the variable v ;
Naturally,
1. λ(ε) = 0 ;
2. λ(u) = 1 for u ∈ Σ ;
3. λ(u1 · u2 · · · uk) = k
i=1 λ(ui), if ui is an expression for
i = 1, 2, . . . , k ;
4. λ(ϕ(u)) = |ϕ| · λ(u), if ϕ is uniform and u is an
expression.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 13 / 25

50. Is the problem difficult ?
Theorem
Let Σ, V, M and A be some sets of constants, variables,
morphisms and antimorphisms ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 14 / 25

51. Is the problem difficult ?
Theorem
Let Σ, V, M and A be some sets of constants, variables,
morphisms and antimorphisms ;
Let L = R be an equation on these four sets ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 14 / 25

52. Is the problem difficult ?
Theorem
Let Σ, V, M and A be some sets of constants, variables,
morphisms and antimorphisms ;
Let L = R be an equation on these four sets ;
Assume that all variables are of known length and that
|L| = |R| = n ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 14 / 25

53. Is the problem difficult ?
Theorem
Let Σ, V, M and A be some sets of constants, variables,
morphisms and antimorphisms ;
Let L = R be an equation on these four sets ;
Assume that all variables are of known length and that
|L| = |R| = n ;
Then the problem of determining if some solution
S : V → Σ∗ exists for L = R is NP-complete.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 14 / 25

54. Proof of NP-completeness
Clearly in NP ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 15 / 25

55. Proof of NP-completeness
Clearly in NP ;
We reduce 3-IN-1-SAT to the problem ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 15 / 25

56. Proof of NP-completeness
Clearly in NP ;
We reduce 3-IN-1-SAT to the problem ;
Consider an instance of 3-IN-1-SAT :
x =
m
i=1
(xi1 ∨ xi2 ∨ xi3),
where xij ∈ {b1, b1, b2, b2, . . . , bn, bn}.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 15 / 25

57. Proof of NP-completeness
Clearly in NP ;
We reduce 3-IN-1-SAT to the problem ;
Consider an instance of 3-IN-1-SAT :
x =
m
i=1
(xi1 ∨ xi2 ∨ xi3),
where xij ∈ {b1, b1, b2, b2, . . . , bn, bn}.
We construct an instance of words equation as follows.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 15 / 25

58. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

59. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Variables : V = {c1, c2, . . . , cm} ∪ {b1, b1, b2, b2, . . . , bn, bn}
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

60. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Variables : V = {c1, c2, . . . , cm} ∪ {b1, b1, b2, b2, . . . , bn, bn}
Lengths :
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

61. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Variables : V = {c1, c2, . . . , cm} ∪ {b1, b1, b2, b2, . . . , bn, bn}
Lengths :
λ(ci) = 3 for i = 1, 2, . . . , m ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

62. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Variables : V = {c1, c2, . . . , cm} ∪ {b1, b1, b2, b2, . . . , bn, bn}
Lengths :
λ(ci) = 3 for i = 1, 2, . . . , m ;
λ(bi) = λ(bi) = 1 for i = 1, 2, . . . , n ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

63. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Variables : V = {c1, c2, . . . , cm} ∪ {b1, b1, b2, b2, . . . , bn, bn}
Lengths :
λ(ci) = 3 for i = 1, 2, . . . , m ;
λ(bi) = λ(bi) = 1 for i = 1, 2, . . . , n ;
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

64. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Variables : V = {c1, c2, . . . , cm} ∪ {b1, b1, b2, b2, . . . , bn, bn}
Lengths :
λ(ci) = 3 for i = 1, 2, . . . , m ;
λ(bi) = λ(bi) = 1 for i = 1, 2, . . . , n ;
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equations :
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

65. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Variables : V = {c1, c2, . . . , cm} ∪ {b1, b1, b2, b2, . . . , bn, bn}
Lengths :
λ(ci) = 3 for i = 1, 2, . . . , m ;
λ(bi) = λ(bi) = 1 for i = 1, 2, . . . , n ;
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equations :
c1c2 · · · cm = x11x12x13x21 · · · xm3.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

66. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Variables : V = {c1, c2, . . . , cm} ∪ {b1, b1, b2, b2, . . . , bn, bn}
Lengths :
λ(ci) = 3 for i = 1, 2, . . . , m ;
λ(bi) = λ(bi) = 1 for i = 1, 2, . . . , n ;
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equations :
c1c2 · · · cm = x11x12x13x21 · · · xm3.
ϕ(ci) = 1, for i = 1, 2, . . . , m ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

67. Reduction
Constants : Σ = {0, 1} ∪ {$1, $2, . . . , $m+n}
Variables : V = {c1, c2, . . . , cm} ∪ {b1, b1, b2, b2, . . . , bn, bn}
Lengths :
λ(ci) = 3 for i = 1, 2, . . . , m ;
λ(bi) = λ(bi) = 1 for i = 1, 2, . . . , n ;
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equations :
c1c2 · · · cm = x11x12x13x21 · · · xm3.
ϕ(ci) = 1, for i = 1, 2, . . . , m ;
ϕ(bibi) = 1, for i = 1, 2, . . . , n ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 16 / 25

68. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

69. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

70. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

71. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

72. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
=
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

73. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)
=
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

74. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)
=
1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

75. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1
=
1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

76. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1
=
1 $1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

77. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)
=
1 $1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

78. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)
=
1 $1 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

79. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2
=
1 $1 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

80. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2
=
1 $1 1 $2
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

81. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)
=
1 $1 1 $2
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

82. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)
=
1 $1 1 $2 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

83. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3
=
1 $1 1 $2 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

84. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3
=
1 $1 1 $2 1 $3
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

85. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1)
=
1 $1 1 $2 1 $3
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

86. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1)
=
1 $1 1 $2 1 $3 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

87. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4
=
1 $1 1 $2 1 $3 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

88. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4
=
1 $1 1 $2 1 $3 1 $4
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

89. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2)
=
1 $1 1 $2 1 $3 1 $4
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

90. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2)
=
1 $1 1 $2 1 $3 1 $4 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

91. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2) $5
=
1 $1 1 $2 1 $3 1 $4 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

92. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2) $5
=
1 $1 1 $2 1 $3 1 $4 1 $5
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

93. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2) $5 ϕ(c3)
=
1 $1 1 $2 1 $3 1 $4 1 $5
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

94. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2) $5 ϕ(c3)
=
1 $1 1 $2 1 $3 1 $4 1 $5 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

95. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2) $5 ϕ(c3) $6
=
1 $1 1 $2 1 $3 1 $4 1 $5 1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

96. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2) $5 ϕ(c3) $6
=
1 $1 1 $2 1 $3 1 $4 1 $5 1 $6
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

97. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2) $5 ϕ(c3) $6 c1 c2 c3
=
1 $1 1 $2 1 $3 1 $4 1 $5 1 $6
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

98. Reduction (cont.)
Consider the boolean expression
x = (b1 ∨ ¬b2 ∨ b3) ∧ (¬b1 ∨ ¬b3 ∨ b4) ∧ (¬b2 ∨ b3 ∨ ¬b4).
Constants : Σ = {0, 1} ∪ {$1, $2, $3, $4, $5, $6}
Variables : V = {c1, c2, c3} ∪ {b1, b1, b2, b2, b3, b3, b4, b4}
Morphism : ϕ(0) = ε ; ϕ(1) = 1 ;
Equation :
ϕ(b1b1)$1 ϕ(b2b2)$2 ϕ(b3b3)$3 ϕ(c1) $4 ϕ(c2) $5 ϕ(c3) $6 c1 c2 c3
=
1 $1 1 $2 1 $3 1 $4 1 $5 1 $6 b1b2b3b1b3b4b2b3b4
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 17 / 25

99. Outline
1. Introduction
2. Words equations
3. From equations to graphs
4. Conclusion
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 18 / 25

100. Example 1 (only with words)
Consider the length 20 equation
uuv = wwx
where |u| = 4, |v| = 12, |w| = 6, |x| = 8.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 19 / 25

101. Example 1 (only with words)
Consider the length 20 equation
uuv = wwx
where |u| = 4, |v| = 12, |w| = 6, |x| = 8.
We create the following graph :
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 19 / 25

102. Example 1 (only with words)
Consider the length 20 equation
uuv = wwx
where |u| = 4, |v| = 12, |w| = 6, |x| = 8.
We create the following graph :
e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14 e15 e16 e17 e18 e19 e20
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 19 / 25

103. Example 1 (only with words)
Consider the length 20 equation
uuv = wwx
where |u| = 4, |v| = 12, |w| = 6, |x| = 8.
We create the following graph :
e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14 e15 e16 e17 e18 e19 e20
u1 u2 u3 u4
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 19 / 25

104. Example 1 (only with words)
Consider the length 20 equation
uuv = wwx
where |u| = 4, |v| = 12, |w| = 6, |x| = 8.
We create the following graph :
e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14 e15 e16 e17 e18 e19 e20
u1 u2 u3 u4
w1 w2 w3 w4 w5 w6
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 19 / 25

105. Example 1 (only with words)
Consider the length 20 equation
uuv = wwx
where |u| = 4, |v| = 12, |w| = 6, |x| = 8.
We create the following graph :
u1, u3, e1, e3, e5, e7, e9, e11, w1, w3, w5
u2, u4, e2, e4, e6, e8, e10, e12, w2, w4, w6
e13
e14
e15
e16
e17
e18
e19
e20
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 19 / 25

106. Example 2 (tilings)
Next, consider the length 36 equation
(xLyLˆxLˆyL)2
= uzLtLˆzLˆtLv,
where |x| = 3, |y| = 4, |z| = 3, |t| = 4, |u| = 3, |v| = 15.
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 20 / 25

107. Example 2 (tilings)
Next, consider the length 36 equation
(xLyLˆxLˆyL)2
= uzLtLˆzLˆtLv,
where |x| = 3, |y| = 4, |z| = 3, |t| = 4, |u| = 3, |v| = 15.
We create the following graph :
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 20 / 25

108. Example 2 (tilings)
Next, consider the length 36 equation
(xLyLˆxLˆyL)2
= uzLtLˆzLˆtLv,
where |x| = 3, |y| = 4, |z| = 3, |t| = 4, |u| = 3, |v| = 15.
We create the following graph :
e1, e19, x1, ˆt3
e6, e24, y2, z3
e10, e28, ˆx1, t3 e15, e33, ˆy2, ˆz3
L, e3, e4, e7, e9,
e12, e13, e16,
e18, x3, z1, y3,
t2, ˆx3, ˆz1, ˆy3, ˆt2
¯·¯·
¯· ¯·
e2, e20, x2, ˆt4
e8, e26, y4, t1
e14, e32, ˆy1, ˆz2
e5, e23, y1, z2
e17, e35, ˆy4, ˆt1
e11, e29, ˆx2, t4
¯·¯·
¯·
¯· ¯·
¯·
e2, e14, e17, e20,
e32, e35, x2, ˆy1,
ˆy4, ˆt4, ˆz2, ˆt1
e5, e8, e11, e23,
e26, e29, y1, y4,
ˆx2, z2, t1, t4
¯·
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 20 / 25

109. Example 2 (tilings)
Next, consider the length 36 equation
(xLyLˆxLˆyL)2
= uzLtLˆzLˆtLv,
where |x| = 3, |y| = 4, |z| = 3, |t| = 4, |u| = 3, |v| = 15.
We create the following graph :
e2, e20, x2, ˆt4
e8, e26, y4, t1
e14, e32, ˆy1, ˆz2
e5, e23, y1, z2
e17, e35, ˆy4, ˆt1
e11, e29, ˆx2, t4
¯·¯·
¯·
¯· ¯·
¯·
R, e1, e6, e10,
e15, e19, e24,
e28, e33, x1,
y2, ˆx1, ˆy2,
ˆt3, z3, t3, ˆz3
L, e3, e4, e7, e9,
e12, e13, e16,
e18, x3, z1, y3,
t2, ˆx3, ˆz1, ˆy3, ˆt2
¯·
e2, e14, e17, e20,
e32, e35, x2, ˆy1,
ˆy4, ˆt4, ˆz2, ˆt1
e5, e8, e11, e23,
e26, e29, y1, y4,
ˆx2, z2, t1, t4
¯·
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 20 / 25

110. Reduction rules
Vertices with unlabelled edges are merged :
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 21 / 25

111. Reduction rules
Vertices with unlabelled edges are merged :
u v
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 21 / 25

112. Reduction rules
Vertices with unlabelled edges are merged :
u v u, v
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 21 / 25

113. Reduction rules
Vertices with unlabelled edges are merged :
u v u, v
Constants are propagated :
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 21 / 25

114. Reduction rules
Vertices with unlabelled edges are merged :
u v u, v
Constants are propagated :
a u
ϕ
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 21 / 25

115. Reduction rules
Vertices with unlabelled edges are merged :
u v u, v
Constants are propagated :
a u
ϕ
a u, ϕ(a)
ϕ
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 21 / 25

116. Reduction rules
Vertices with unlabelled edges are merged :
u v u, v
Constants are propagated :
a u
ϕ
a u, ϕ(a)
ϕ
Morphisms are functions :
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 21 / 25

117. Reduction rules
Vertices with unlabelled edges are merged :
u v u, v
Constants are propagated :
a u
ϕ
a u, ϕ(a)
ϕ
Morphisms are functions :
u
v1
v2
ϕ
ϕ
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 21 / 25

118. Reduction rules
Vertices with unlabelled edges are merged :
u v u, v
Constants are propagated :
a u
ϕ
a u, ϕ(a)
ϕ
Morphisms are functions :
u
v1
v2
ϕ
ϕ
u v1, v2
ϕ
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 21 / 25

119. Reduction rules (cont.)
Morphisms can be combined :
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 22 / 25

120. Reduction rules (cont.)
Morphisms can be combined :
u1
u2
u3
u4
ϕ1
ϕ2
ϕ3
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 22 / 25

121. Reduction rules (cont.)
Morphisms can be combined :
u1
u2
u3
u4
ϕ1
ϕ2
ϕ3
u1
u2
u3
u4
ϕ1
ϕ2
ϕ3
ϕ2 ◦ ϕ1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 22 / 25

122. Reduction rules (cont.)
Morphisms can be combined :
u1
u2
u3
u4
ϕ1
ϕ2
ϕ3
u1
u2
u3
u4
ϕ1
ϕ2
ϕ3
ϕ2 ◦ ϕ1
ϕ3 ◦ ϕ2
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 22 / 25

123. Reduction rules (cont.)
Morphisms can be combined :
u1
u2
u3
u4
ϕ1
ϕ2
ϕ3
u1
u2
u3
u4
ϕ1
ϕ2
ϕ3
ϕ2 ◦ ϕ1
ϕ3 ◦ ϕ2
ϕ3 ◦ ϕ2 ◦ ϕ1
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 22 / 25

124. Outline
1. Introduction
2. Words equations
3. From equations to graphs
4. Conclusion
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 23 / 25

125. Concluding remarks
The approach based on graphs was compared with one
using directly boolean constraint programming ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 24 / 25

126. Concluding remarks
The approach based on graphs was compared with one
using directly boolean constraint programming ;
In almost all cases, it performed better, especially when
there are morphisms and antimorphisms ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 24 / 25

127. Concluding remarks
The approach based on graphs was compared with one
using directly boolean constraint programming ;
In almost all cases, it performed better, especially when
there are morphisms and antimorphisms ;
Equations considered in this talk :
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 24 / 25

128. Concluding remarks
The approach based on graphs was compared with one
using directly boolean constraint programming ;
In almost all cases, it performed better, especially when
there are morphisms and antimorphisms ;
Equations considered in this talk :
have fixed lengths ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 24 / 25

129. Concluding remarks
The approach based on graphs was compared with one
using directly boolean constraint programming ;
In almost all cases, it performed better, especially when
there are morphisms and antimorphisms ;
Equations considered in this talk :
have fixed lengths ;
deal only with uniform morphisms and
antimorphisms ;
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 24 / 25

130. Concluding remarks
The approach based on graphs was compared with one
using directly boolean constraint programming ;
In almost all cases, it performed better, especially when
there are morphisms and antimorphisms ;
Equations considered in this talk :
have fixed lengths ;
deal only with uniform morphisms and
antimorphisms ;
How could it be extended to the non-uniform case ?
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 24 / 25

131. Questions ?
Merci de m’avoir ´ecout´e
Thank you for your attention
Les agradezco su atenci´on
Blondin Mass´e et al. (LIF, UQAC) March 13th, 2014 25 / 25