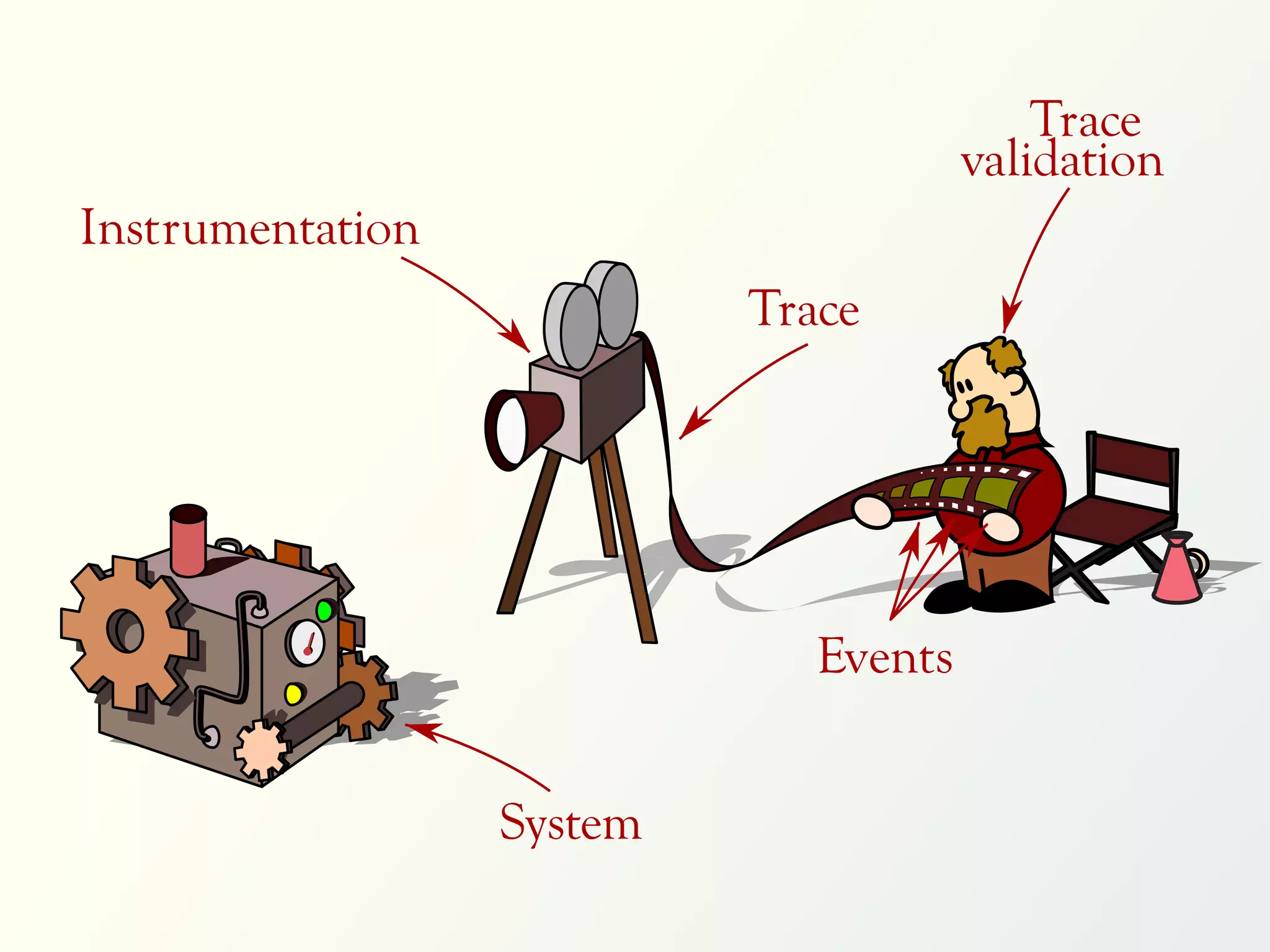
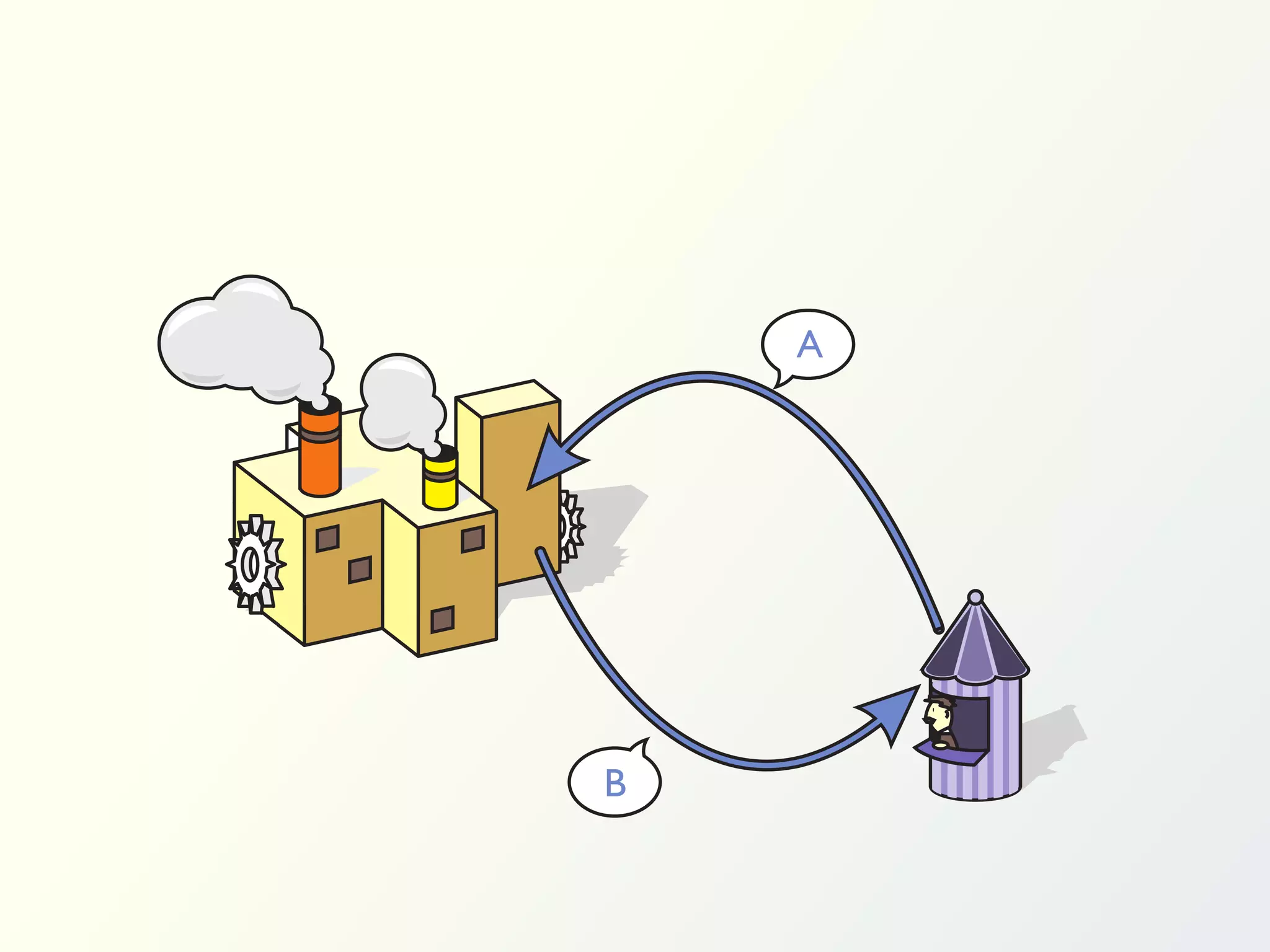
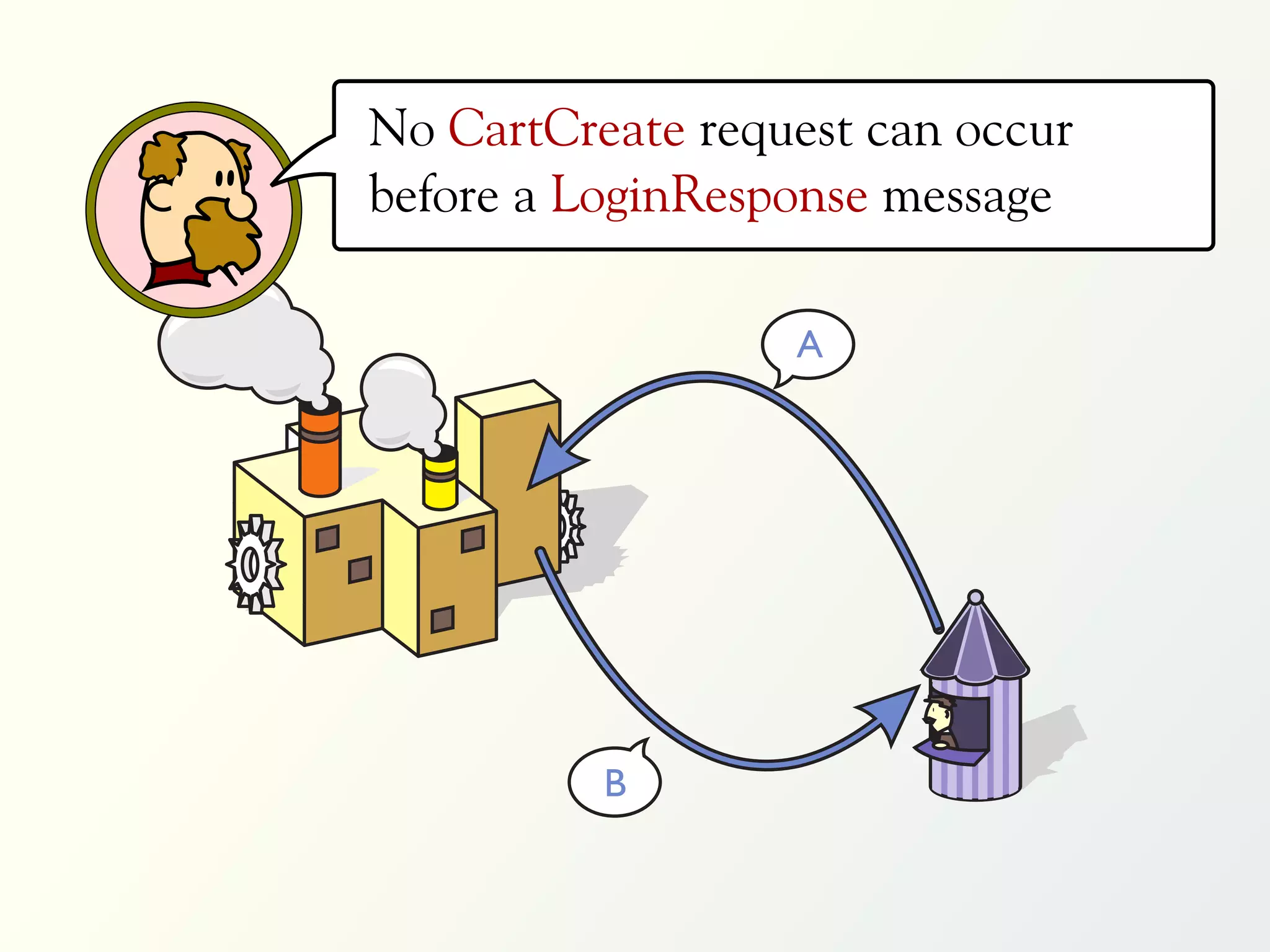
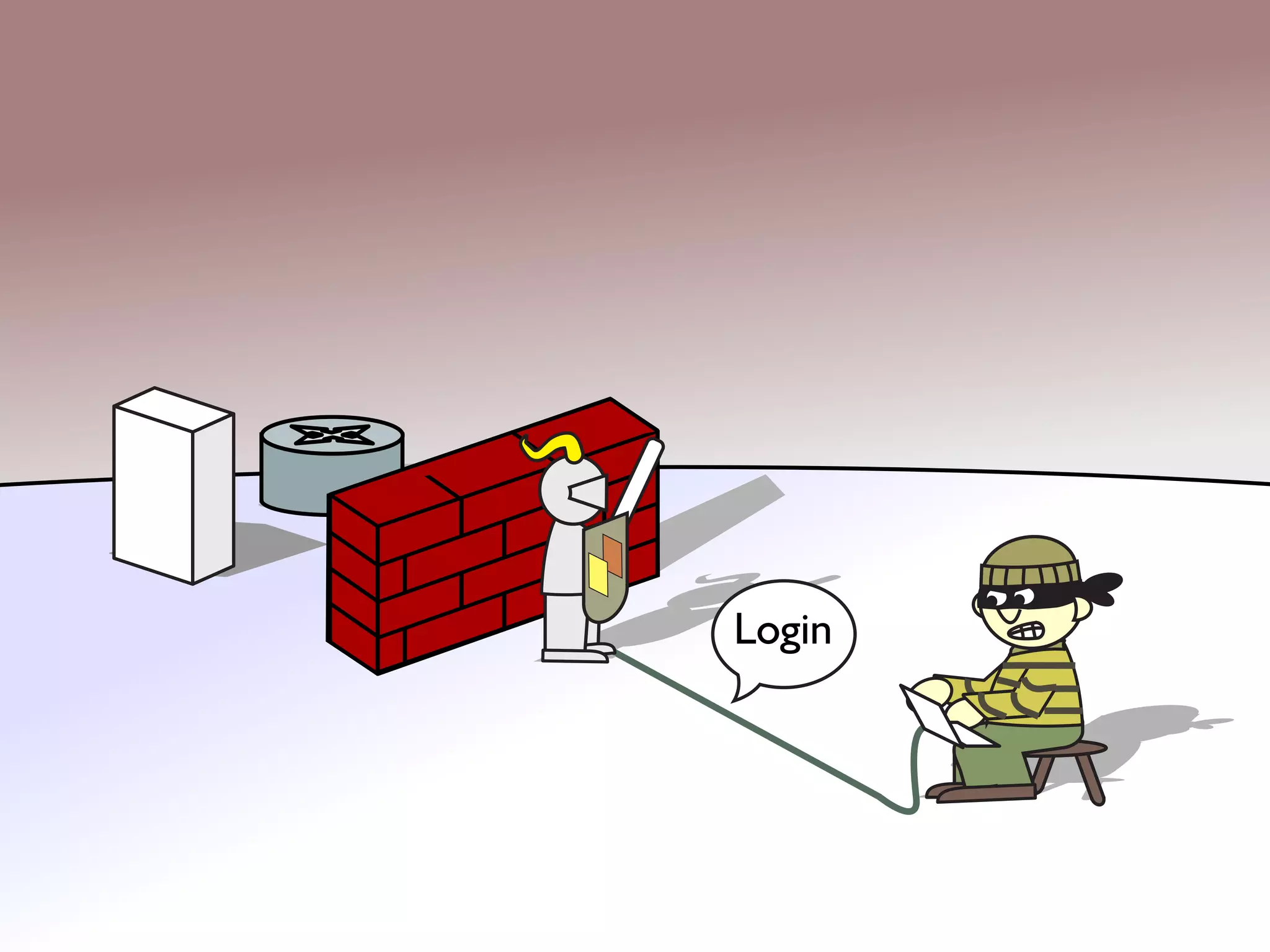
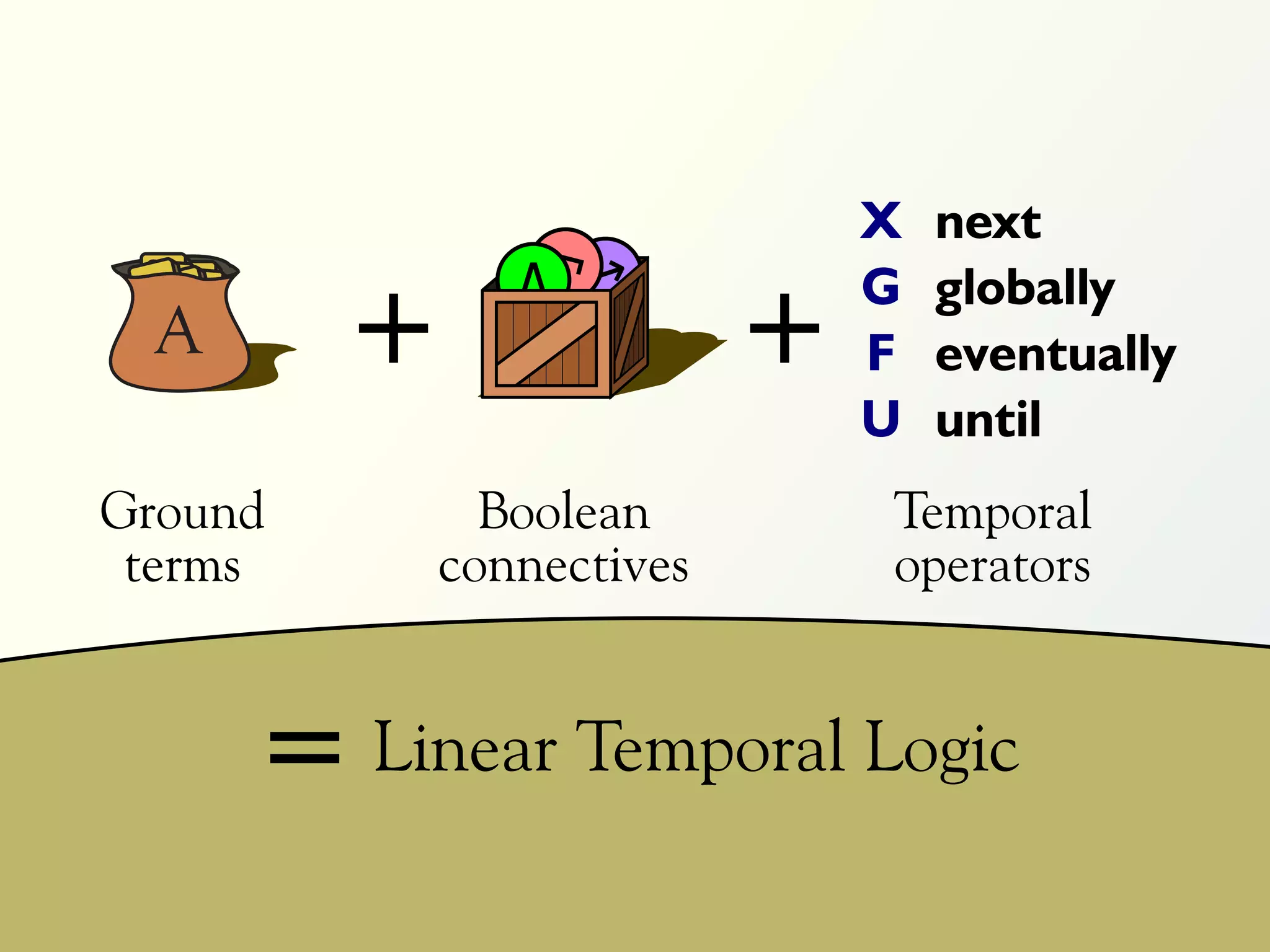
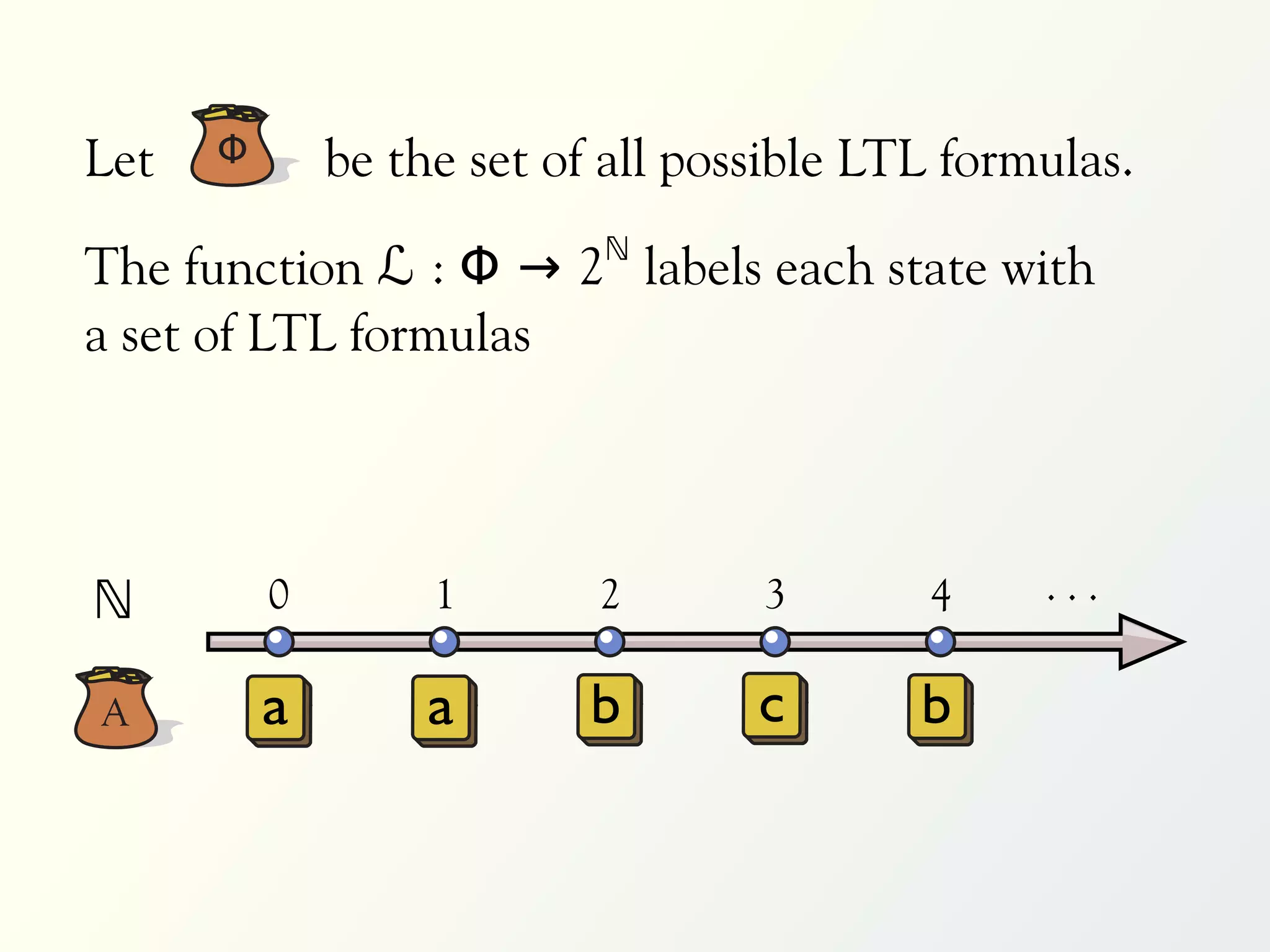
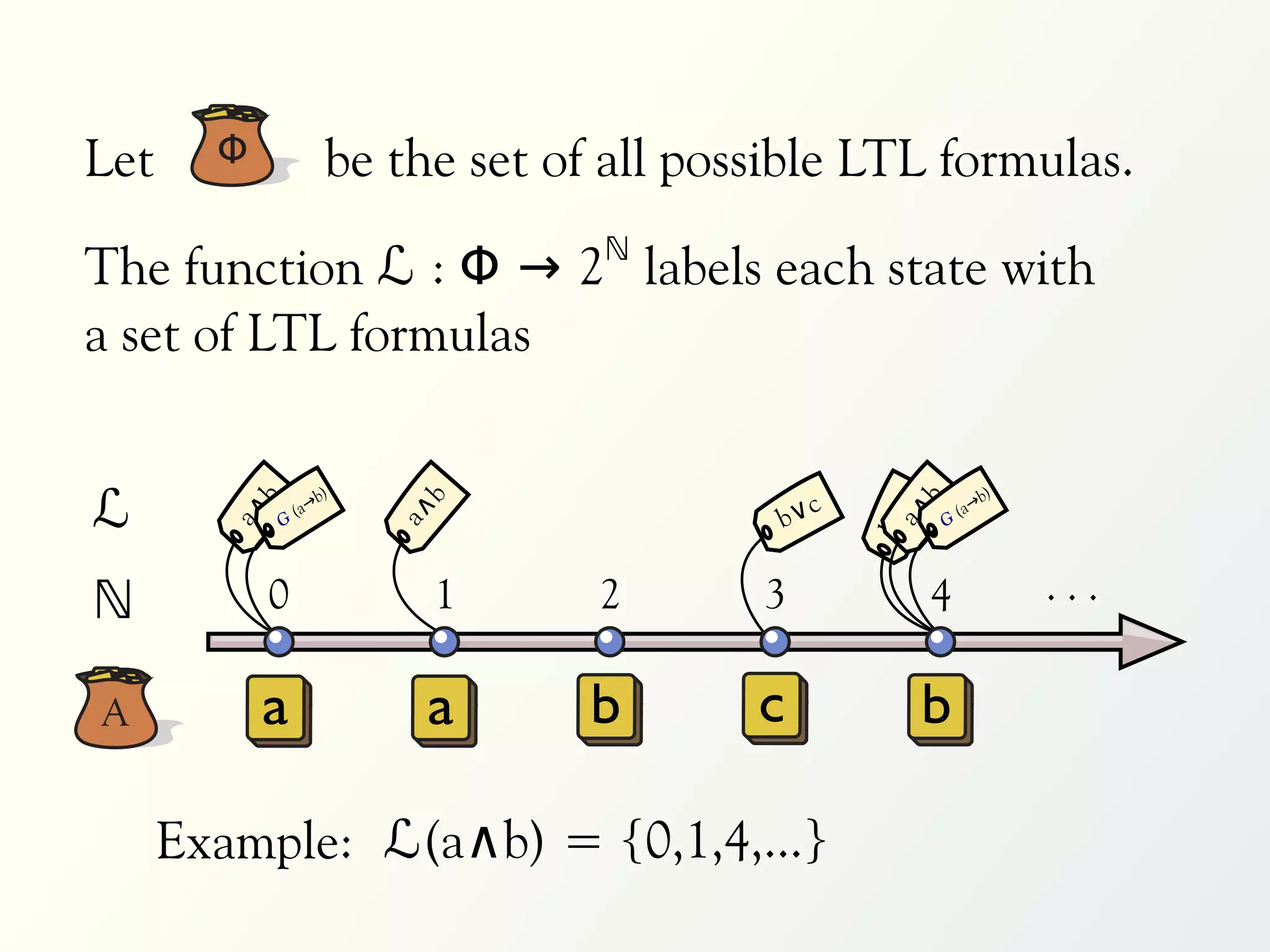
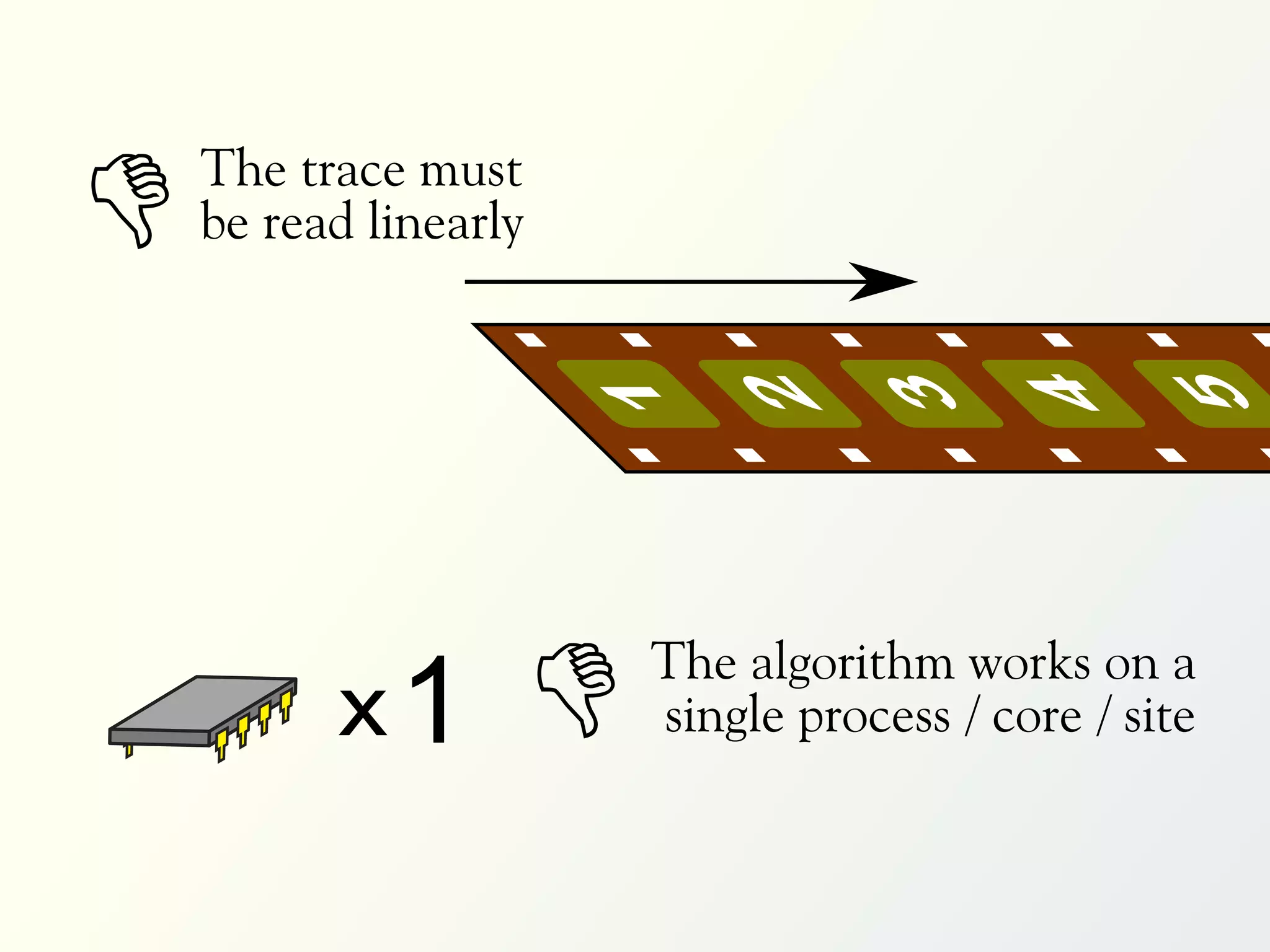
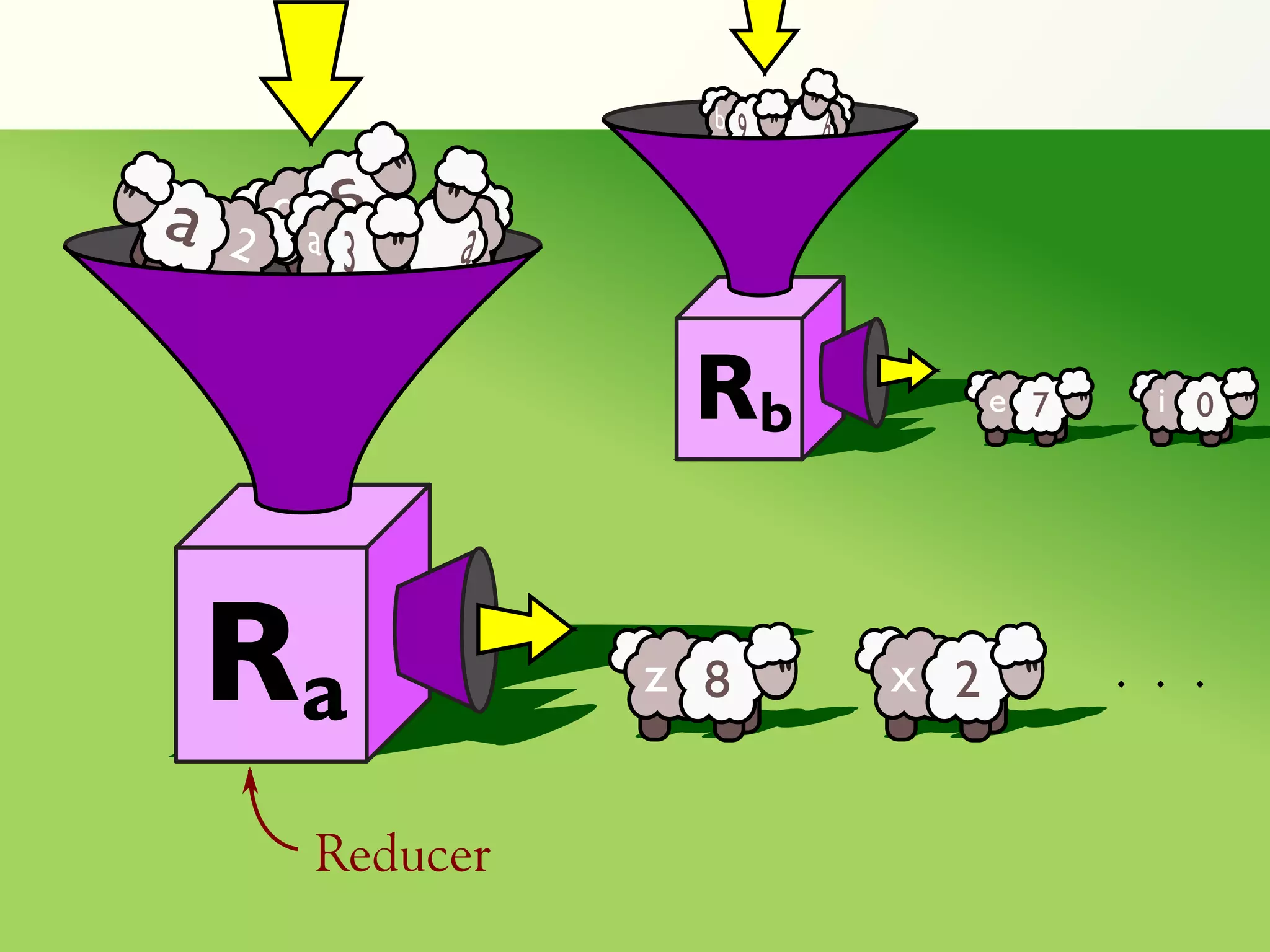
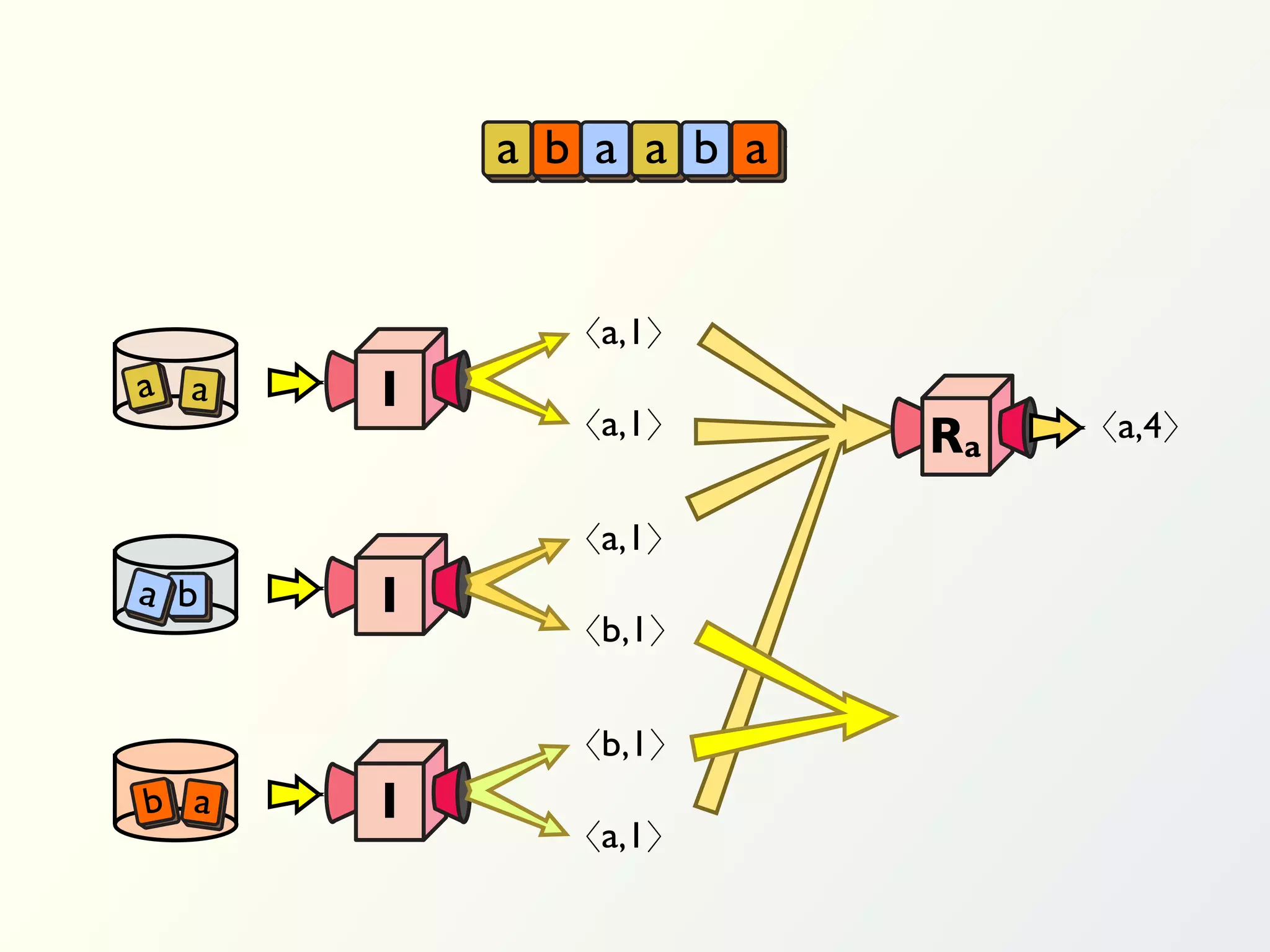
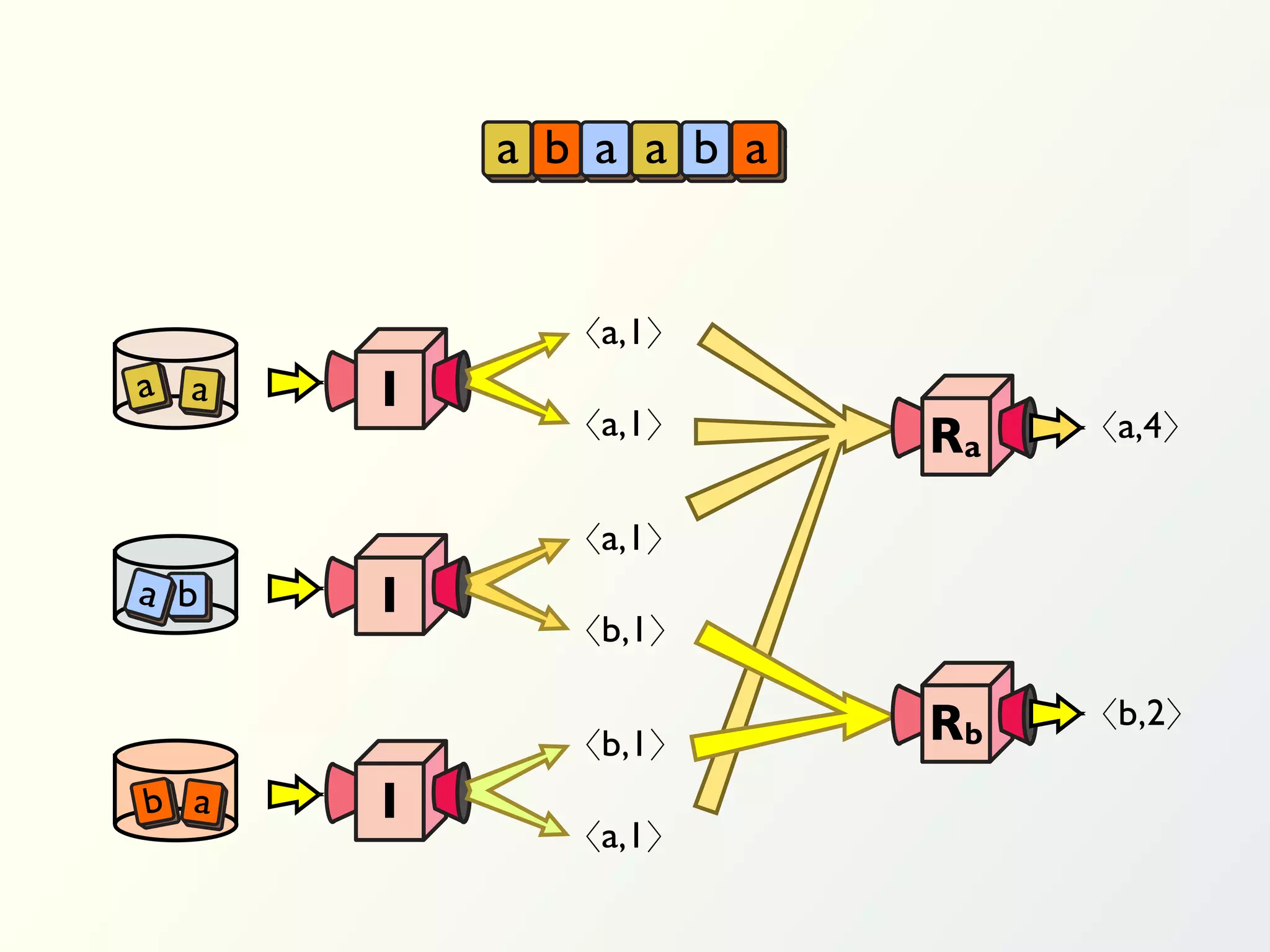
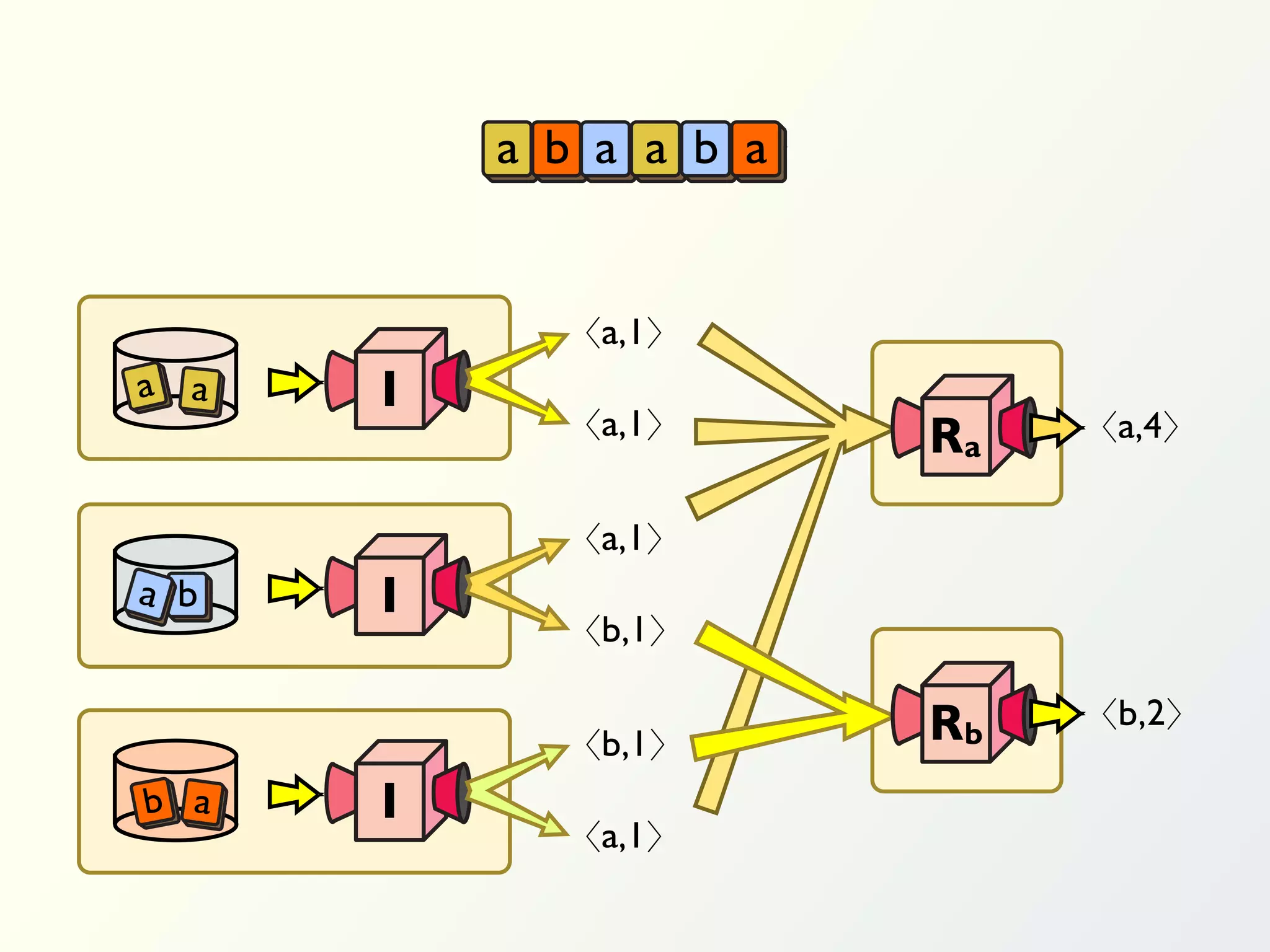
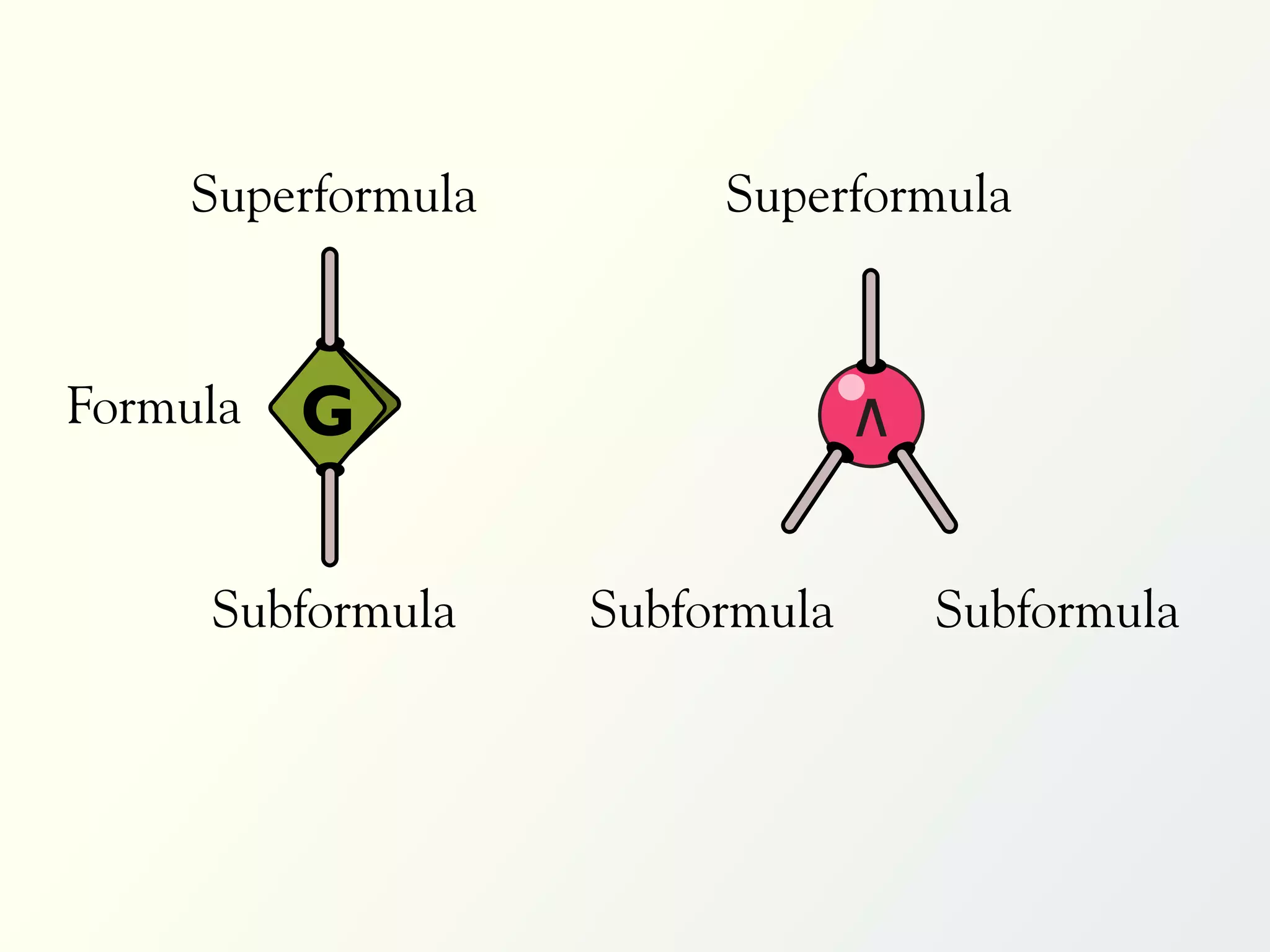
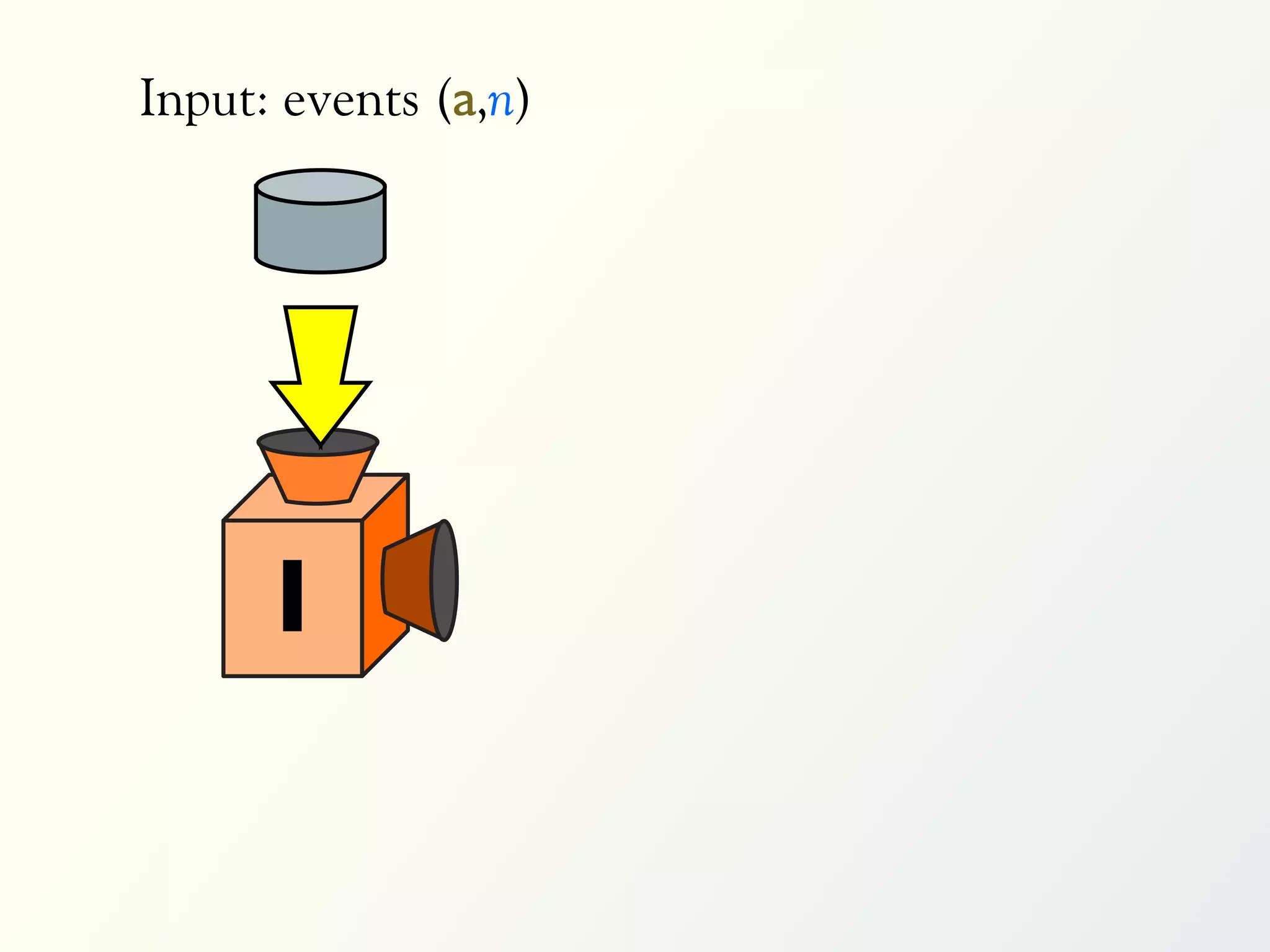
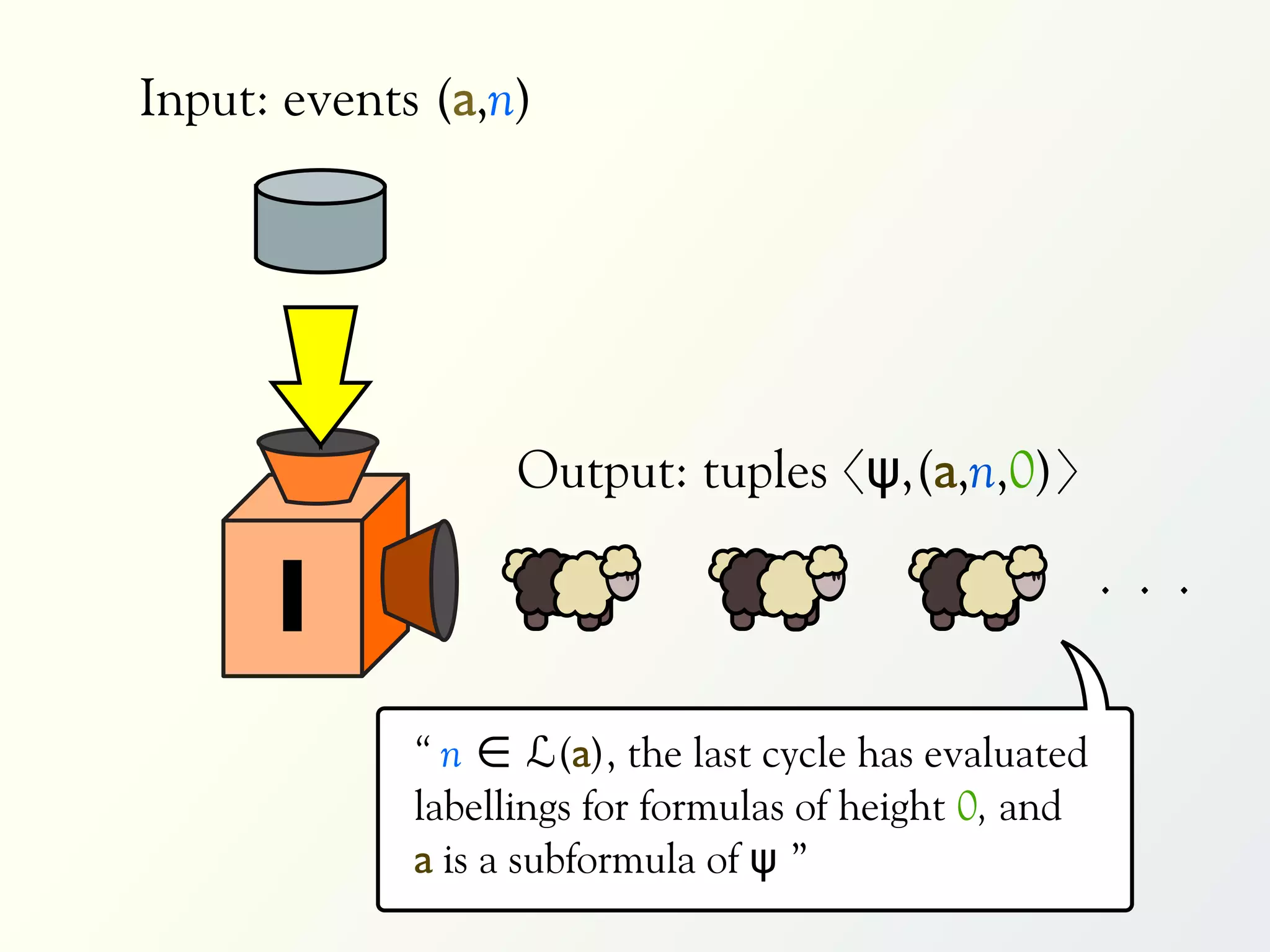
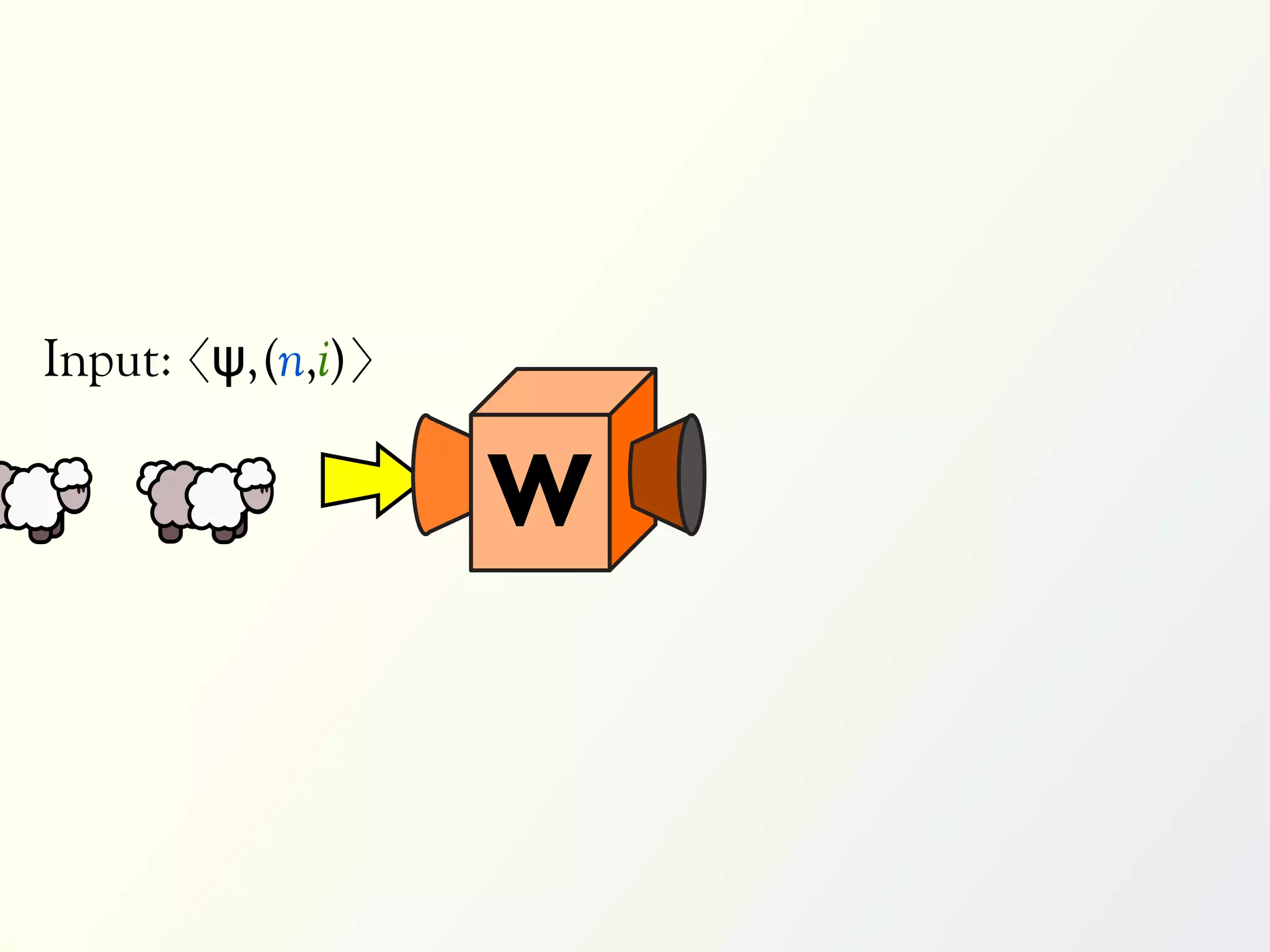
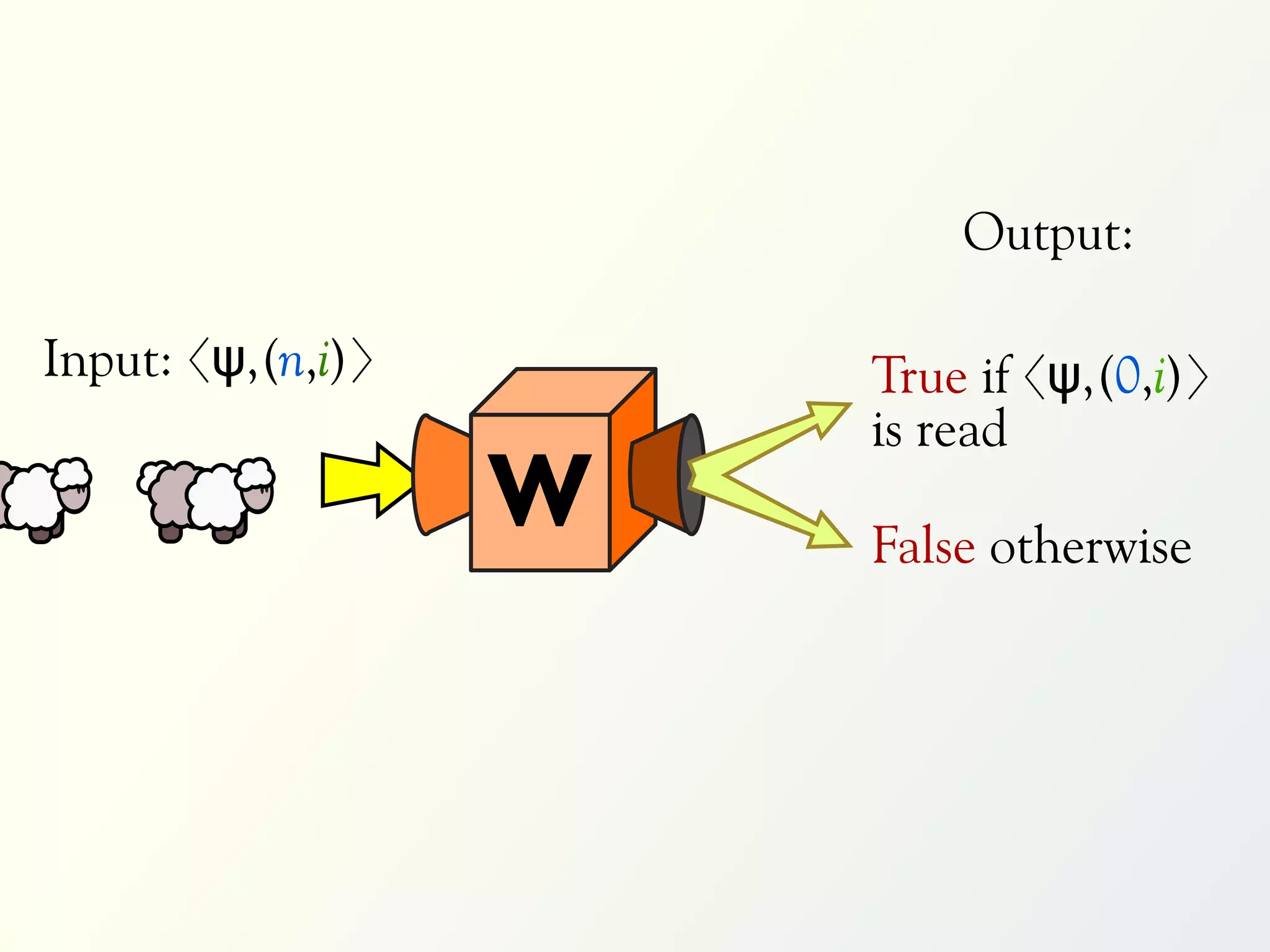
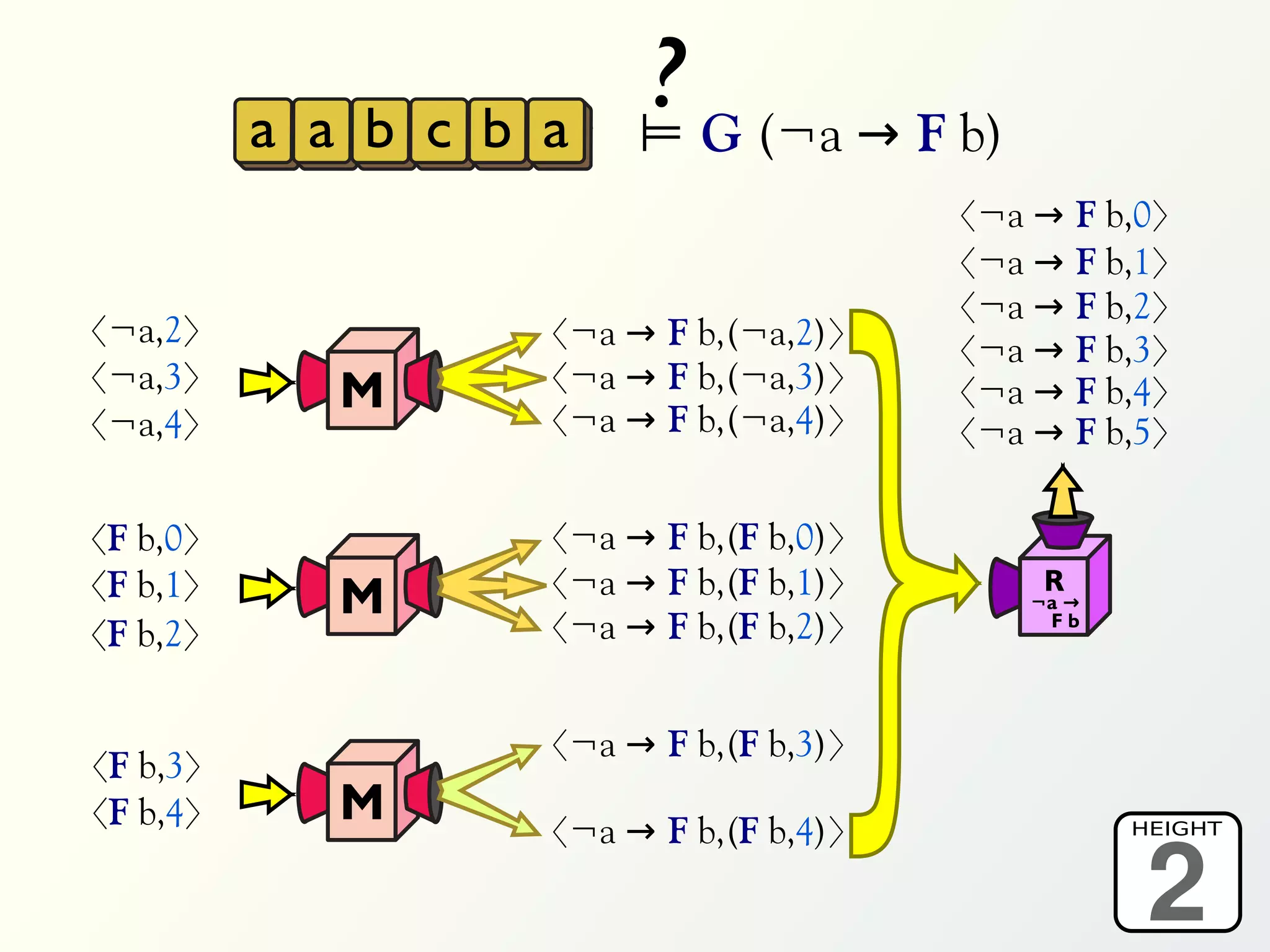
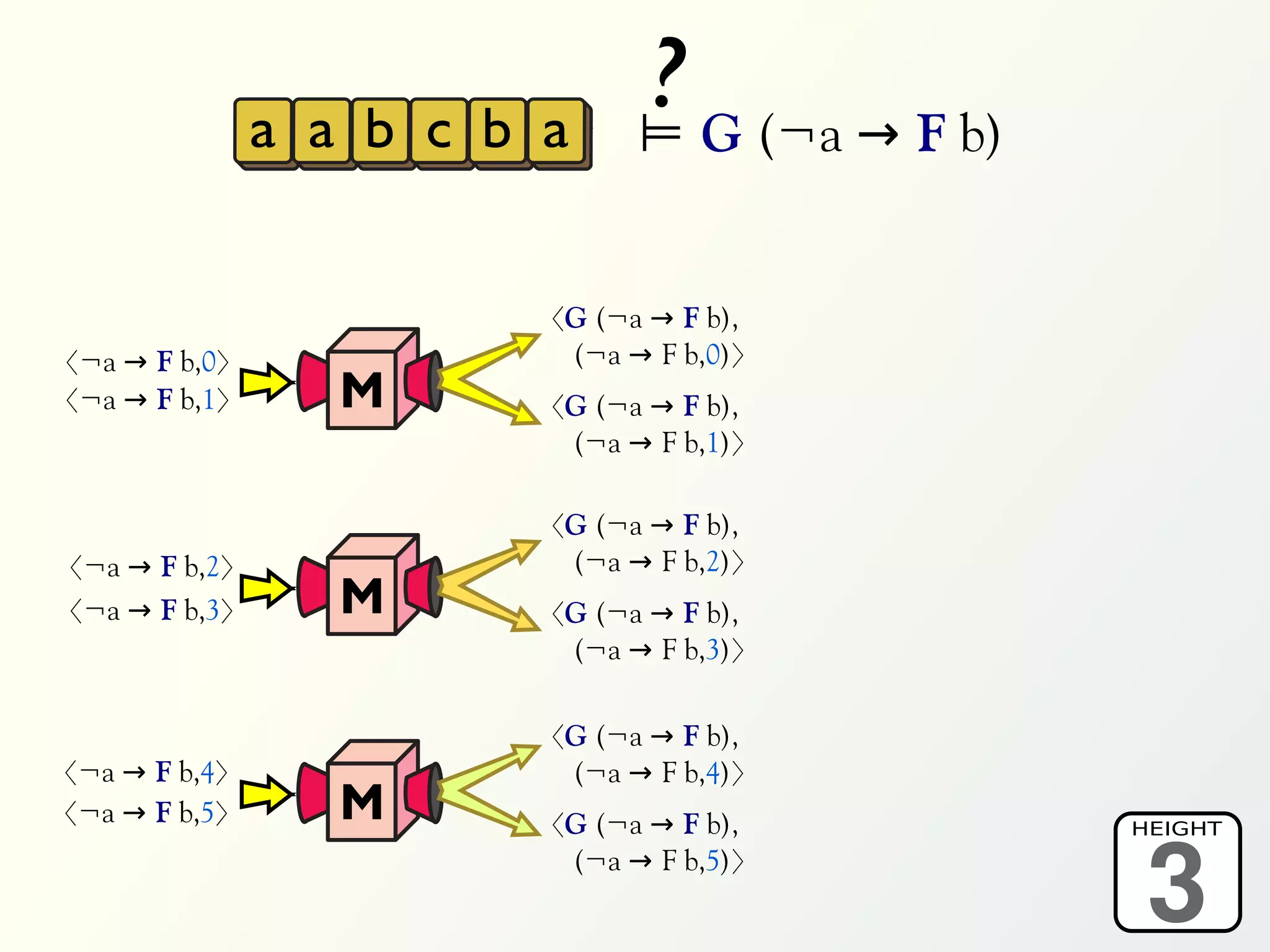
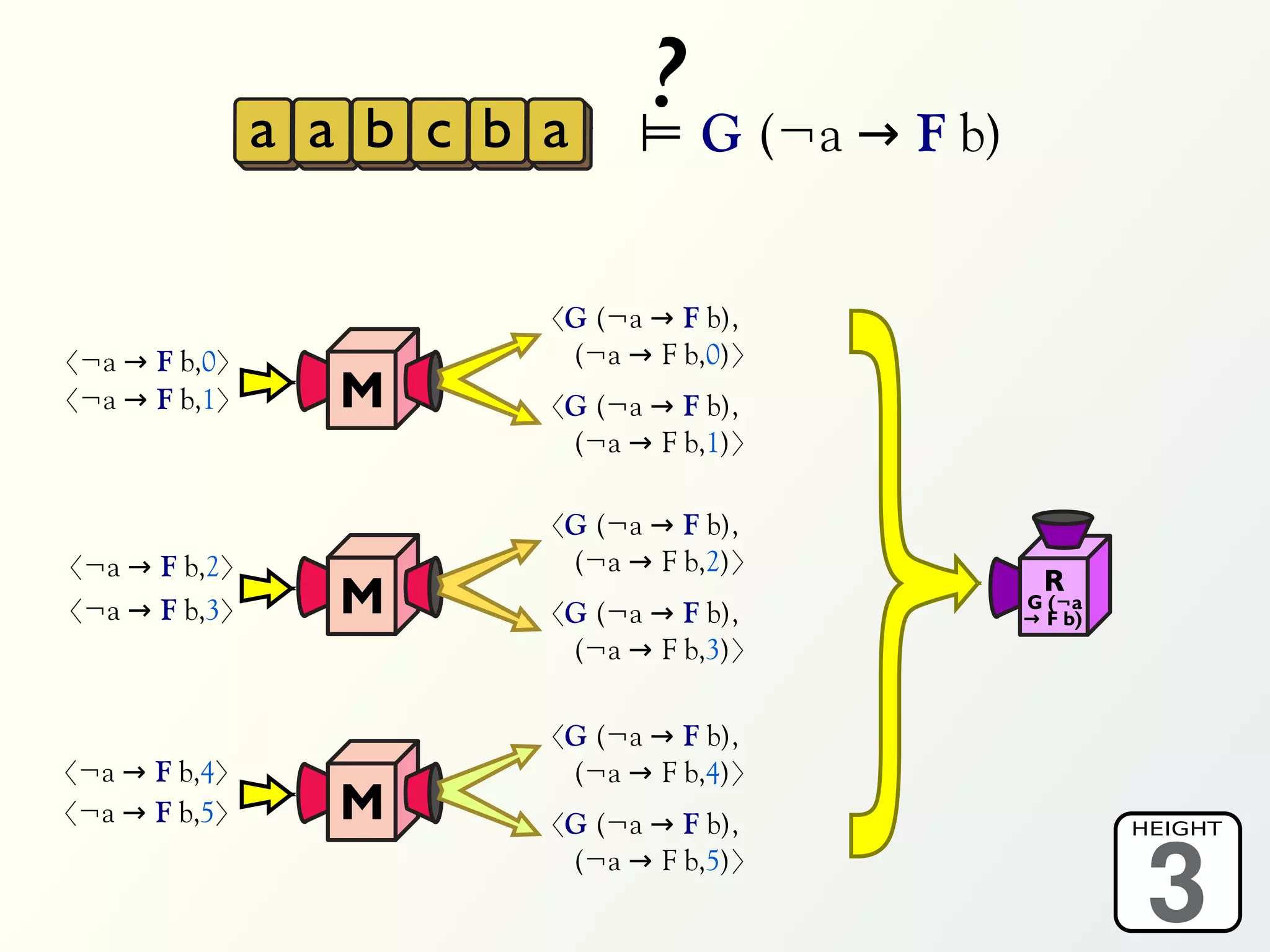
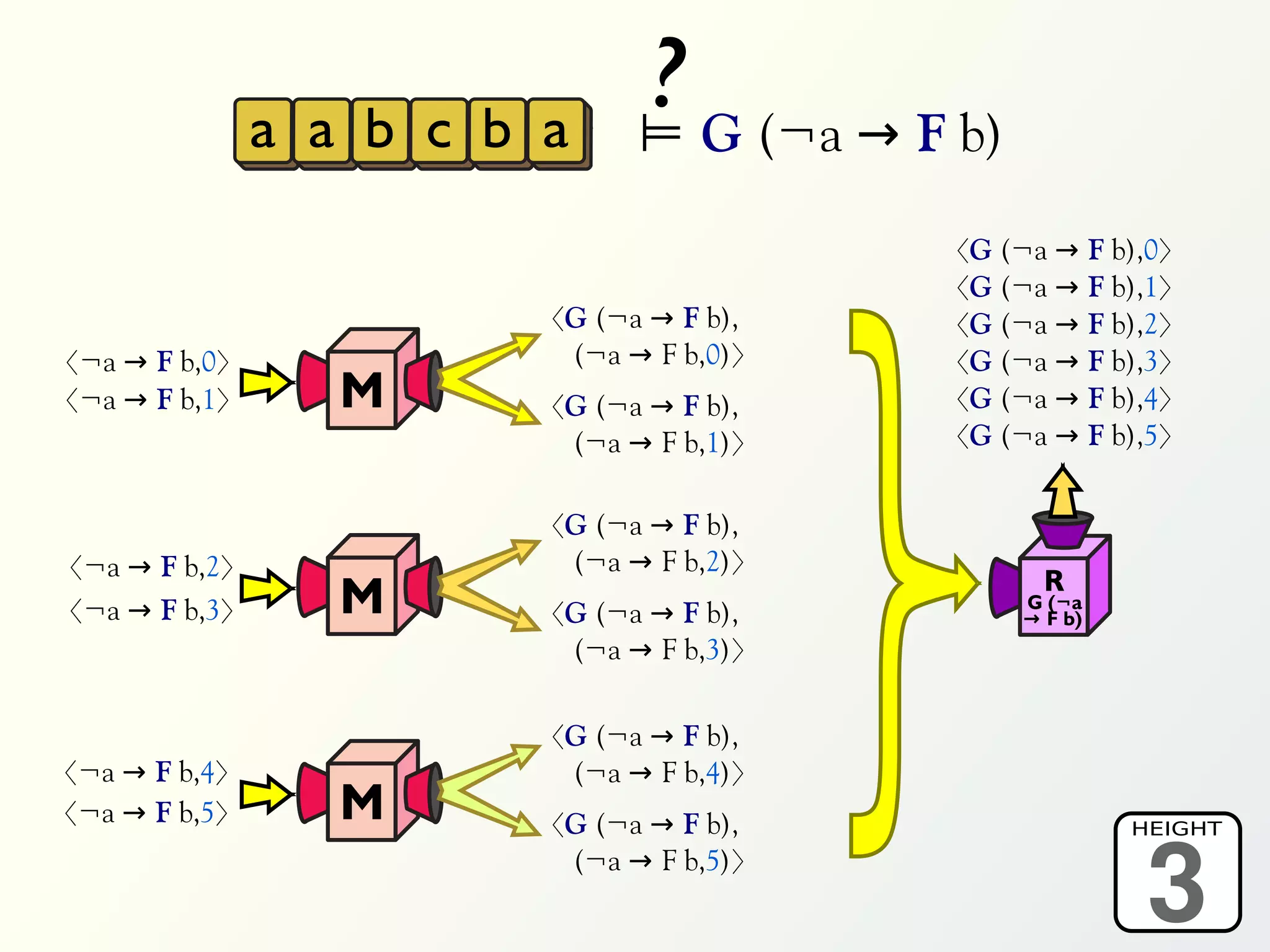
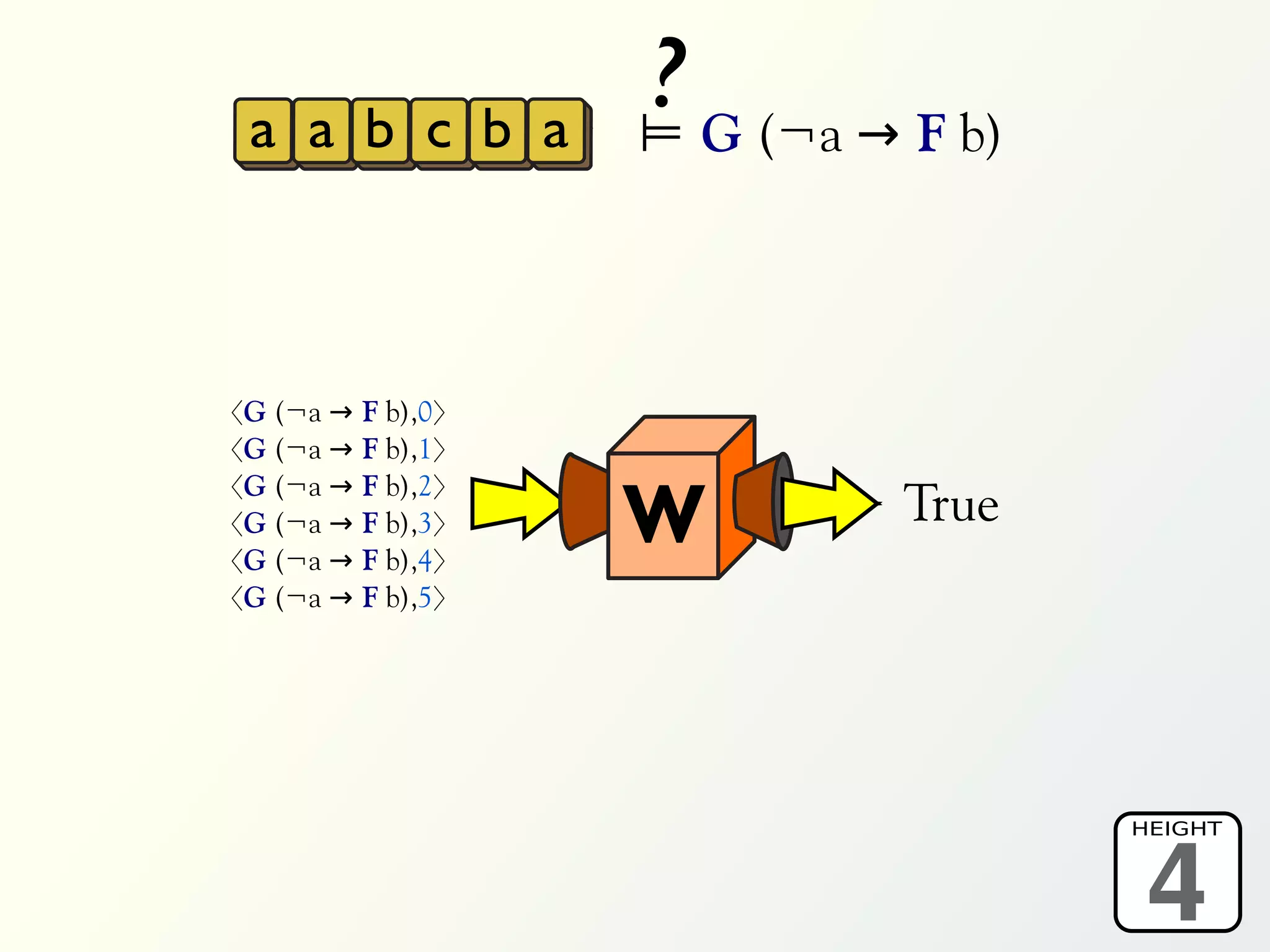
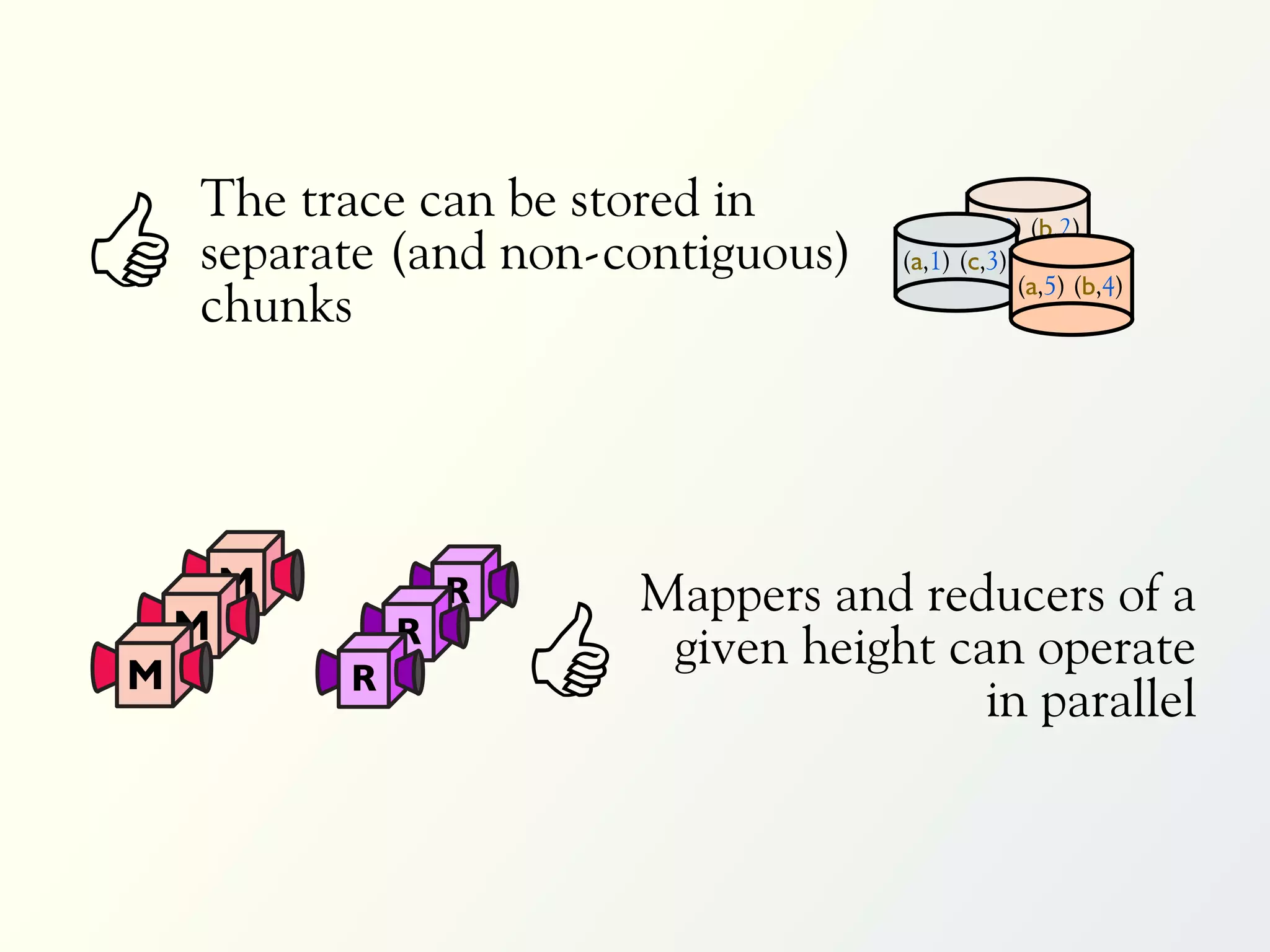
The document discusses a parallel algorithm for validating linear temporal logic (LTL) properties using a MapReduce framework. It outlines the methodology for labeling event traces, evaluating temporal formulas, and ensuring correct execution flow in various scenarios via defined rules and theorems. The approach emphasizes the ability to perform computations in parallel, aiming to enhance efficiency in checking system properties against specified conditions.

1. MapReduce for Parallel
Trace Validation of LTL Properties
Benjamin Barre, Mathieu Klein, Maxime Soucy-Boivin,
Pierre-Antoine Ollivier and Sylvain Hallé
Université du Québec à Chicoutimi
CANADA
Fonds de recherche
Nature et
NSERC technologies
CRSNG

3. System

4. System

5. Instrumentation
System

6. Instrumentation
System

7. Instrumentation
Trace
System

8. Instrumentation
Trace
Events
System

9. Instrumentation
Trace
Events
System

10. Trace
validation
Instrumentation
Trace
Events
System

11. or<T>
Iterat

12. hasNext
or<T>
Iterat
next

13. A call to next must be preceded
by a call to hasNext
hasNext
or<T>
Iterat
next

14. A
B

15. No CartCreate request can occur
before a LoginResponse message
A
B

16. Login

17. Three successive login attempts
should trigger an alarm
Login

19. Receive order

20. Ready?
Receive order

21. Ready? Yes
Receive order

22. Ready? Yes
Receive order No Ship
File order

23. A received order must eventually
be shipped
Ready? Yes
Receive order No Ship
File order

24. Let A be a set of event symbols.
A trace m is a mapping from ℕ to
the set of events :
ℕ 0 1 2 3 4 ...
A a a b c b

25. X next
¬
∧ → G globally
A + ∧¬→ + F eventually
U until
Ground Boolean Temporal
terms connectives operators
= Linear Temporal Logic

26. Let Φ be the set of all possible LTL formulas.
The function ℒ : Φ → 2ℕ labels each state with
a set of LTL formulas
ℕ 0 1 2 3 4 ...
A a a b c b

27. Let Φ be the set of all possible LTL formulas.
The function ℒ : Φ → 2ℕ labels each state with
a set of LTL formulas
ℒ b)
∨c
b)
b
b
b
(a→ (a→
a∧c
b
a∧
a∧
b∨
G G
ℕ 0 1 2 3 4 ...
A a a b c b
Example: ℒ(a∧b) = {0,1,4,...}

28. i ∈ ℒ(a) ⇔ m(i) = a
i ∈ ℒ(¬φ) ⇔ i ∉ ℒ(φ)
i ∈ ℒ(φ∧ψ) ⇔ i ∈ ℒ(φ) and i ∈ ℒ(ψ)
i ∈ ℒ(φ∨ψ) ⇔ i ∈ ℒ(φ) or i ∈ ℒ(ψ)
i ∈ ℒ(X φ) ⇔ i+1 ∈ ℒ(φ)
i ∈ ℒ(G φ) ⇔ j ∈ ℒ(φ) for all j ≥ i
i ∈ ℒ(F φ) ⇔ j ∈ ℒ(φ) for some j ≥ i
i ∈ ℒ(φ U ψ) ⇔ j ∈ ℒ(ψ) for some j ≥ i and
k ∈ ℒ(φ) for all j ≥ k ≥ i

29. Theorem
i ∈ ℒ(φ) exactly when the trace
m(i), m(i+1), ... satisfies φ
σ
φ
ψ
0 1 2 3 4 ...

30. Theorem
i ∈ ℒ(φ) exactly when the trace
m(i), m(i+1), ... satisfies φ
σ
φ
ψ
0 1 2 3 4 ...
Therefore...
0 ∈ ℒ(φ) ⇔ m ⊧ φ

31. A call to next must be followed by a call
to hasNext
No CartCreate request can occur
before a LoginResponse message
A received order must eventually
be shipped
Three successive login attempts should
trigger an alarm

32. A call to next must be followed by a call
to hasNext
G (next → X hasNext)
No CartCreate request can occur
before a LoginResponse message
A received order must eventually
be shipped
Three successive login attempts should
trigger an alarm

33. A call to next must be followed by a call
to hasNext
G (next → X hasNext)
No CartCreate request can occur
before a LoginResponse message
¬ CartCreate U hasNext
A received order must eventually
be shipped
Three successive login attempts should
trigger an alarm

34. A call to next must be followed by a call
to hasNext
G (next → X hasNext)
No CartCreate request can occur
before a LoginResponse message
¬ CartCreate U hasNext
A received order must eventually
be shipped
G (receive → F ship)
Three successive login attempts should
trigger an alarm

35. A call to next must be followed by a call
to hasNext
G (next → X hasNext)
No CartCreate request can occur
before a LoginResponse message
¬ CartCreate U hasNext
A received order must eventually
be shipped
G (receive → F ship)
Three successive login attempts should
trigger an alarm
G ¬(fail ∧ (X (fail ∧ X fail)))

36. Iterat
or<T>
Java MOP

37. � The trace must
be read linearly
2
3
4
5
1
� The algorithm works on a
x1 single process / core / site

38. 10,000,000
1,000,000
100,000
10,000
1,000
100
10
1
1970 1980 1990 2000 2010

39. 10,000,000 Transistors (x1000)
1,000,000
100,000
10,000
1,000
100
10
1
1970 1980 1990 2000 2010

40. 10,000,000 Transistors (x1000)
1,000,000
100,000
10,000 CPU Speed
1,000 (MHz)
100
10
1
1970 1980 1990 2000 2010

41. PageRank
f ∞

42. Value
Key
a 1
{ Tuple (baaah)

43. Data source

44. Data source
II
Input reader

45. Data source
II a 2 z 7 . . .
Input reader

46. . . . a 2
a 2

47. Mapper
. . . a 2
a 2 M

48. Mapper
. . . a 2
a 2 M w 6
a 2
. . .

49. Mapper
. . . a 2
a 2 M w 6
a 2
. . .
a b
3
a2
3
3 g
b

50. a 3 a3 2a e 38 a
a3 b 9 bb
a 3
b
a
a

51. e 38 a b
. . .
. . .
b
db
Shuffling
aa
b
a ab
a a 2
a
b 9
3

52. b 9 b
a a
2 2a 3 a

53. b 9 b
a a
2 2a 3 a
Rb
Ra
Reducer

54. b 9 b
a a
2 2a 3 a
Rb e 7 i 0
Ra z 8 x 2 . . .
Reducer

55. a b a a b a

56. a b a a b a
a a
a b
b a

57. a b a a b a
a a I
a b
b a

58. a b a a b a
〈a,1〉
a a I
〈a,1〉
a b
b a

59. a b a a b a
〈a,1〉
a a I
〈a,1〉
〈a,1〉
a b I
〈b,1〉
〈b,1〉
b a I
〈a,1〉

60. a b a a b a
〈a,1〉
a a I
〈a,1〉
〈a,1〉
a b I
〈b,1〉
〈b,1〉
b a I
〈a,1〉

61. a b a a b a
〈a,1〉
a a I
〈a,1〉
〈a,1〉
a b I
〈b,1〉
〈b,1〉
b a I
〈a,1〉

62. a b a a b a
〈a,1〉
a a I
〈a,1〉 Ra
〈a,1〉
a b I
〈b,1〉
〈b,1〉
b a I
〈a,1〉

63. a b a a b a
〈a,1〉
a a I
〈a,1〉 Ra 〈a,4〉
〈a,1〉
a b I
〈b,1〉
〈b,1〉
b a I
〈a,1〉

64. a b a a b a
〈a,1〉
a a I
〈a,1〉 Ra 〈a,4〉
〈a,1〉
a b I
〈b,1〉
〈b,1〉 Rb 〈b,2〉
b a I
〈a,1〉

65. a b a a b a
〈a,1〉
a a I
〈a,1〉 Ra 〈a,4〉
〈a,1〉
a b I
〈b,1〉
〈b,1〉 Rb 〈b,2〉
b a I
〈a,1〉

66. Superformula Superformula
Formula G ∧
Subformula Subformula Subformula

67. 4
G
Height
3 →
2 ∧
3
1 2
¬ F
1
0
0 a c b

68. 4
G
Height
3 →
2 ∧
3
1 2
¬ F
1
0
0 a c b
¬c has height 1
G ((a ∧¬c) → F b) has height 4

69. i ∈ ℒ(a) ⇔ m(i) = a
i ∈ ℒ(¬φ) ⇔ i ∉ ℒ(φ)
i ∈ ℒ(φ∧ψ) ⇔ i ∈ ℒ(φ) and i ∈ ℒ(ψ)
i ∈ ℒ(φ∨ψ) ⇔ i ∈ ℒ(φ) or i ∈ ℒ(ψ)
i ∈ ℒ(X φ) ⇔ i+1 ∈ ℒ(φ)
i ∈ ℒ(G φ) ⇔ j ∈ ℒ(φ) for all j ≥ i
i ∈ ℒ(F φ) ⇔ j ∈ ℒ(φ) for some j ≥ i
i ∈ ℒ(φ U ψ) ⇔ j ∈ ℒ(ψ) for some j ≥ i and
k ∈ ℒ(φ) for all j ≥ k ≥ i

70. i ∈ ℒ(a) ⇔ m(i) = a
i ∈ ℒ(¬φ) ⇔ i ∉ ℒ(φ)
i ∈ ℒ(φ∧ψ) ⇔ i ∈ ℒ(φ) and i ∈ ℒ(ψ)
i ∈ ℒ(φ∨ψ) ⇔ i ∈ ℒ(φ) or i ∈ ℒ(ψ)
i ∈ ℒ(X φ) ⇔ i+1 ∈ ℒ(φ)
i ∈ ℒ(G φ) ⇔ j ∈ ℒ(φ) for all j ≥ i
i ∈ ℒ(F φ) ⇔ j ∈ ℒ(φ) for some j ≥ i
i ∈ ℒ(φ U ψ) ⇔ j ∈ ℒ(ψ) for some j ≥ i and
k ∈ ℒ(φ) for all j ≥ k ≥ i
The labelling of a formula depends only
on labellings of formulas of strictly lower height

71. i ∈ ℒ(a) ⇔ m(i) = a
i ∈ ℒ(¬φ) ⇔ i ∉ ℒ(φ)
i ∈ ℒ(φ∧ψ) ⇔ i ∈ ℒ(φ) and i ∈ ℒ(ψ)
i ∈ ℒ(φ∨ψ) ⇔ i ∈ ℒ(φ) or i ∈ ℒ(ψ)
i ∈ ℒ(X φ) ⇔ i+1 ∈ ℒ(φ)
i ∈ ℒ(G φ) ⇔ j ∈ ℒ(φ) for all j ≥ i
i ∈ ℒ(F φ) ⇔ j ∈ ℒ(φ) for some j ≥ i
i ∈ ℒ(φ U ψ) ⇔ j ∈ ℒ(ψ) for some j ≥ i and
k ∈ ℒ(φ) for all j ≥ k ≥ i
The labelling of a formula depends only
on labellings of formulas of strictly lower height
⇒ All labellings of formulas of same height are
independent

72. i ∈ ℒ(a) ⇔ m(i) = a
i ∈ ℒ(¬φ) ⇔ i ∉ ℒ(φ)
i ∈ ℒ(φ∧ψ) ⇔ i ∈ ℒ(φ) and i ∈ ℒ(ψ)
i ∈ ℒ(φ∨ψ) ⇔ i ∈ ℒ(φ) or i ∈ ℒ(ψ)
i ∈ ℒ(X φ) ⇔ i+1 ∈ ℒ(φ)
i ∈ ℒ(G φ) ⇔ j ∈ ℒ(φ) for all j ≥ i
i ∈ ℒ(F φ) ⇔ j ∈ ℒ(φ) for some j ≥ i
i ∈ ℒ(φ U ψ) ⇔ j ∈ ℒ(ψ) for some j ≥ i and
k ∈ ℒ(φ) for all j ≥ k ≥ i
The labelling of a formula depends only
on labellings of formulas of strictly lower height
⇒ All labellings of formulas of same height are
independent
⇒ They can be computed in parallel

73. M

74. M
Input: tuples 〈φ,(n,i)〉

75. M
Input: tuples 〈φ,(n,i)〉
“ n ∈ ℒ(φ), and the last cycle has evaluated
labellings for formulas of height i ”

76. “Lift” ℒ(φ) to superformulas of φ
M
Input: tuples 〈φ,(n,i)〉
“ n ∈ ℒ(φ), and the last cycle has evaluated
labellings for formulas of height i ”

77. Output: tuples 〈ψ,(φ,n,i)〉
“Lift” ℒ(φ) to superformulas of φ
M
Input: tuples 〈φ,(n,i)〉
“ n ∈ ℒ(φ), and the last cycle has evaluated
labellings for formulas of height i ”

78. Output: tuples 〈ψ,(φ,n,i)〉
“ n ∈ ℒ(φ), the last cycle has evaluated
labellings for formulas of height i, and
φ is a subformula of ψ ”
“Lift” ℒ(φ) to superformulas of φ
M
Input: tuples 〈φ,(n,i)〉
“ n ∈ ℒ(φ), and the last cycle has evaluated
labellings for formulas of height i ”

79. Rψ

80. Input:
〈ψ,(φ,n,i)〉
Rψ

81. Input:
〈ψ,(φ,n,i)〉
Rψ
“ n ∈ ℒ(φ), the last cycle
has evaluated labellings for
formulas of height i, and
φ is a subformula of ψ ”

82. Input: Compute ℒ(ψ)
〈ψ,(φ,n,i)〉
Rψ
“ n ∈ ℒ(φ), the last cycle
has evaluated labellings for
formulas of height i, and
φ is a subformula of ψ ”

83. Input: Compute ℒ(ψ) Output:
〈ψ,(φ,n,i)〉 〈ψ,(n,i+1)〉
Rψ
“ n ∈ ℒ(φ), the last cycle
has evaluated labellings for
formulas of height i, and
φ is a subformula of ψ ”

84. Input: Compute ℒ(ψ) Output:
〈ψ,(φ,n,i)〉 〈ψ,(n,i+1)〉
Rψ
“ n ∈ ℒ(φ), the last cycle “ n ∈ ℒ(ψ), and the last
has evaluated labellings for cycle has evaluated
formulas of height i, and labellings for formulas of
φ is a subformula of ψ ” height i+1

85. I

86. Input: events (a,n)
I

87. Input: events (a,n)
Output: tuples 〈ψ,(a,n,0)〉
I . . .
“ n ∈ ℒ(a), the last cycle has evaluated
labellings for formulas of height 0, and
a is a subformula of ψ ”

88. W

89. Input: 〈ψ,(n,i)〉
W

90. Output:
Input: 〈ψ,(n,i)〉 True if 〈ψ,(0,i)〉
is read
W False otherwise

91. 3
. . .
R
W
R
2
R
R
R
1
I . . .
R
I R
R

92. 3
. . .
R
W
R
2
R
R
R
1
I . . .
R
I R
R
InputReaders generate the first tuples from
the trace chunks

93. 3
. . .
R
W
R
2
R
R
R
1
I . . .
R
I R
R
The tuples are shuffled to reducers that compute the
labelling ℒ for formulas of height 1

94. 3
. . .
R
W
R
2
R
R
R
1
I . . .
R
I R
R
Mappers copy the labellings into tuples marked by
superformulas of height 2

95. 3
. . .
R
W
R
2
R
R
R
1
I . . .
R
I R
R
Each reducer computes the labelling of a formula of
height 2 from the labelling of its subformulas

96. 3
. . .
R
W
R
2
R
R
R
1
I . . .
R
I R
R
Mappers copy the labellings into tuples marked by
superformulas of height 3

97. 3
. . .
R
W
R
2
R
R
R
1
I . . .
R
I R
R
Each reducer computes the labelling of a formula of
height 3 from the labelling of its subformulas

98. 3
. . .
R
W
R
2
R
R
R
1
I . . .
R
I R
R
An output writer collects the resulting tuples, and
outputs “true” if it encounters a tuple for state 0

100. a a b c b a
? G (¬a → F b)
⊨

101. a a b c b a
? G (¬a → F b)
⊨
(a,0) (b,2)
(a,1) (c,3)
(a,5) (b,4)
0
HEIGHT

102. a a b c b a
? G (¬a → F b)
⊨
(a,0) (b,2)
I
(a,1) (c,3)
I
(a,5) (b,4)
I
0
HEIGHT

103. a a b c b a
? G (¬a → F b)
⊨
〈¬a,(a,0)〉
(a,0) (b,2)
I
〈F b,(b,2)〉
(a,1) (c,3)
I 〈¬a,(a,1)〉
〈F b,(b,4)〉
(a,5) (b,4)
I
0
1
〈¬a,(a,5)〉 HEIGHT

104. a a b c b a
? G (¬a → F b)
⊨
〈¬a,(a,0)〉
(a,0) (b,2)
I
〈F b,(b,2)〉 R
¬a
(a,1) (c,3)
I 〈¬a,(a,1)〉
R
〈F b,(b,4)〉 Fb
(a,5) (b,4)
I
0
1
〈¬a,(a,5)〉 HEIGHT

105. a a b c b a
? G (¬a → F b)
⊨
〈¬a,(a,0)〉
〈¬a,2〉
(a,0) (b,2)
I 〈¬a,3〉
〈F b,(b,2)〉 R
¬a
〈¬a,4〉
(a,1) (c,3)
I 〈¬a,(a,1)〉 〈F b,0〉
〈F b,1〉
R 〈F b,2〉
〈F b,(b,4)〉 Fb
〈F b,3〉
(a,5) (b,4)
I
0
1
〈¬a,(a,5)〉 b,4〉
〈FHEIGHT

106. a a b c b a
? G (¬a → F b)
⊨
〈¬a,2〉
〈¬a,3〉 M
〈¬a,4〉
〈F b,0〉
〈F b,1〉 M
〈F b,2〉
〈F b,3〉
〈F b,4〉 M
2
HEIGHT

107. a a b c b a
? G (¬a → F b)
⊨
〈¬a,2〉 〈¬a → F b,(¬a,2)〉
〈¬a,3〉 M 〈¬a → F b,(¬a,3)〉
〈¬a,4〉 〈¬a → F b,(¬a,4)〉
〈F b,0〉 〈¬a → F b,(F b,0)〉
〈F b,1〉 〈¬a → F b,(F b,1)〉
M 〈¬a → F b,(F b,2)〉
〈F b,2〉
〈¬a → F b,(F b,3)〉
〈F b,3〉
〈F b,4〉 M 〈¬a → F b,(F b,4)〉
2
HEIGHT

108. a a b c b a
? G (¬a → F b)
⊨
〈¬a,2〉 〈¬a → F b,(¬a,2)〉
〈¬a,3〉 M 〈¬a → F b,(¬a,3)〉
〈¬a,4〉 〈¬a → F b,(¬a,4)〉
〈F b,0〉 〈¬a → F b,(F b,0)〉
〈F b,1〉 〈¬a → F b,(F b,1)〉 R
M 〈¬a → F b,(F b,2)〉
¬a →
Fb
〈F b,2〉
〈¬a → F b,(F b,3)〉
〈F b,3〉
〈F b,4〉 M 〈¬a → F b,(F b,4)〉
2
HEIGHT

109. a a b c b a
? G (¬a → F b)
⊨
〈¬a → F b,0〉
〈¬a → F b,1〉
〈¬a → F b,2〉
〈¬a,2〉 〈¬a → F b,(¬a,2)〉 〈¬a → F b,3〉
〈¬a,3〉 M 〈¬a → F b,(¬a,3)〉 〈¬a → F b,4〉
〈¬a,4〉 〈¬a → F b,(¬a,4)〉 〈¬a → F b,5〉
〈F b,0〉 〈¬a → F b,(F b,0)〉
〈F b,1〉 〈¬a → F b,(F b,1)〉 R
M 〈¬a → F b,(F b,2)〉
¬a →
Fb
〈F b,2〉
〈¬a → F b,(F b,3)〉
〈F b,3〉
〈F b,4〉 M 〈¬a → F b,(F b,4)〉
2
HEIGHT

110. a a b c b a
? G (¬a → F b)
⊨
〈¬a → F b,0〉
〈¬a → F b,1〉 M
〈¬a → F b,2〉
〈¬a → F b,3〉 M
〈¬a → F b,4〉
〈¬a → F b,5〉 M
3
HEIGHT

111. a a b c b a
? G (¬a → F b)
⊨
〈G (¬a → F b),
〈¬a → F b,0〉 (¬a → F b,0)〉
〈¬a → F b,1〉 M 〈G (¬a → F b),
(¬a → F b,1)〉
〈G (¬a → F b),
〈¬a → F b,2〉 (¬a → F b,2)〉
〈¬a → F b,3〉 M 〈G (¬a → F b),
(¬a → F b,3)〉
〈G (¬a → F b),
〈¬a → F b,4〉 (¬a → F b,4)〉
〈¬a → F b,5〉 M 〈G (¬a → F b),
3
HEIGHT
(¬a → F b,5)〉

112. a a b c b a
? G (¬a → F b)
⊨
〈G (¬a → F b),
〈¬a → F b,0〉 (¬a → F b,0)〉
〈¬a → F b,1〉 M 〈G (¬a → F b),
(¬a → F b,1)〉
〈G (¬a → F b),
〈¬a → F b,2〉 (¬a → F b,2)〉
R
〈¬a → F b,3〉 M 〈G (¬a → F b), G (¬a
→ F b)
(¬a → F b,3)〉
〈G (¬a → F b),
〈¬a → F b,4〉 (¬a → F b,4)〉
〈¬a → F b,5〉 M 〈G (¬a → F b),
3
HEIGHT
(¬a → F b,5)〉

113. a a b c b a
? G (¬a → F b)
⊨
〈G (¬a → F b),0〉
〈G (¬a → F b),1〉
〈G (¬a → F b), 〈G (¬a → F b),2〉
〈¬a → F b,0〉 (¬a → F b,0)〉 〈G (¬a → F b),3〉
〈¬a → F b,1〉 M 〈G (¬a → F b), 〈G (¬a → F b),4〉
(¬a → F b,1)〉 〈G (¬a → F b),5〉
〈G (¬a → F b),
〈¬a → F b,2〉 (¬a → F b,2)〉
R
〈¬a → F b,3〉 M 〈G (¬a → F b), G (¬a
→ F b)
(¬a → F b,3)〉
〈G (¬a → F b),
〈¬a → F b,4〉 (¬a → F b,4)〉
〈¬a → F b,5〉 M 〈G (¬a → F b),
3
HEIGHT
(¬a → F b,5)〉

114. a a b c b a
? G (¬a → F b)
⊨
〈G (¬a → F b),0〉
〈G (¬a → F b),1〉
W
〈G (¬a → F b),2〉
〈G (¬a → F b),3〉
〈G (¬a → F b),4〉
〈G (¬a → F b),5〉
4
HEIGHT

115. a a b c b a
? G (¬a → F b)
⊨
〈G (¬a → F b),0〉
〈G (¬a → F b),1〉
W
〈G (¬a → F b),2〉
〈G (¬a → F b),3〉 True
〈G (¬a → F b),4〉
〈G (¬a → F b),5〉
4
HEIGHT

116. The trace can be stored in
� separate (and non-contiguous)
chunks
(a,0) (b,2)
(a,1) (c,3)
(a,5) (b,4)
M R Mappers and reducers of a
M
M
R
R
� given height can operate
in parallel

117. Tests on 500 randomly-generated traces
From 1 to 100,000 events
Each event contains 10 parameters
named p₀ to p₉ with 10 possible values

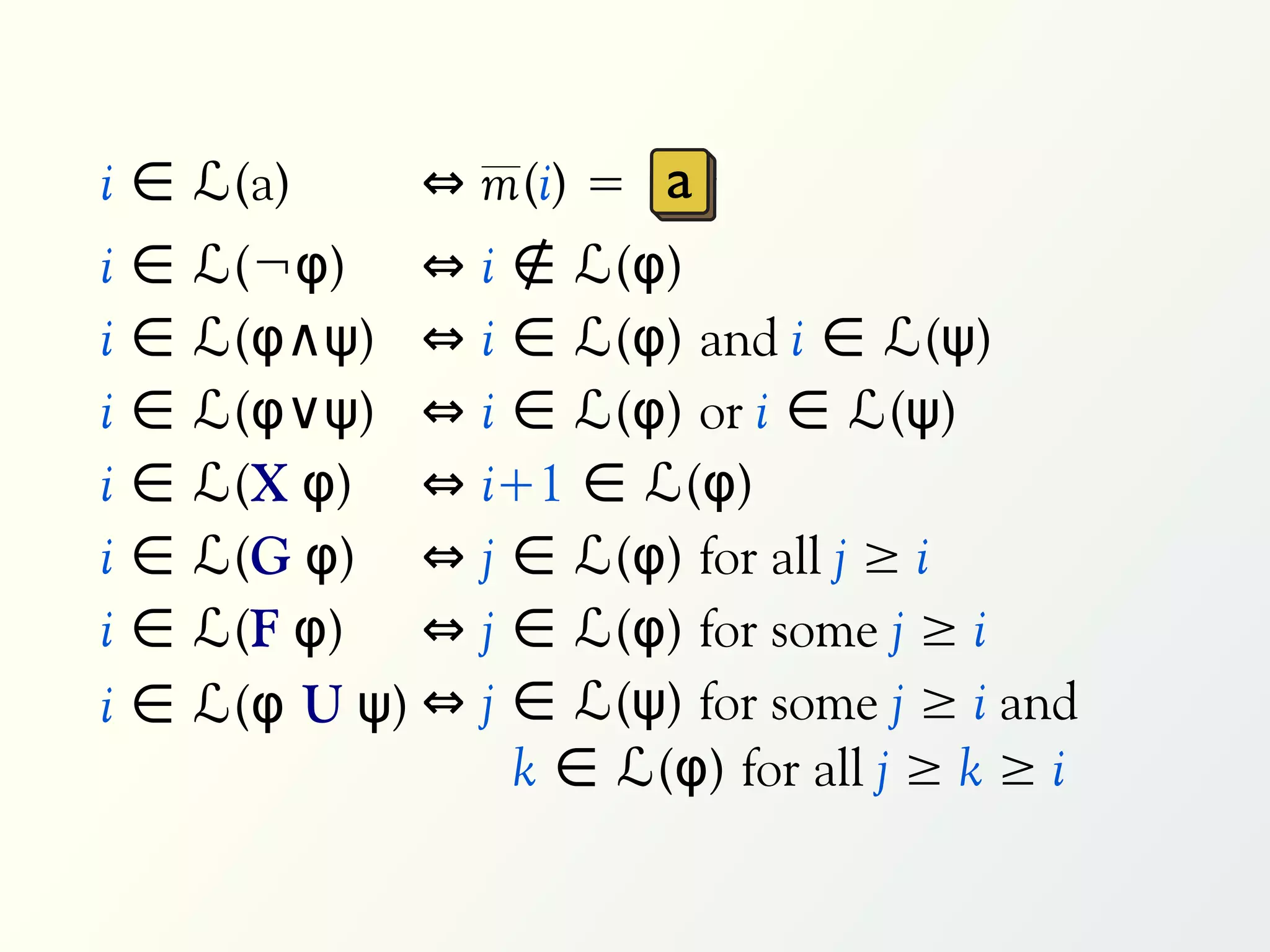
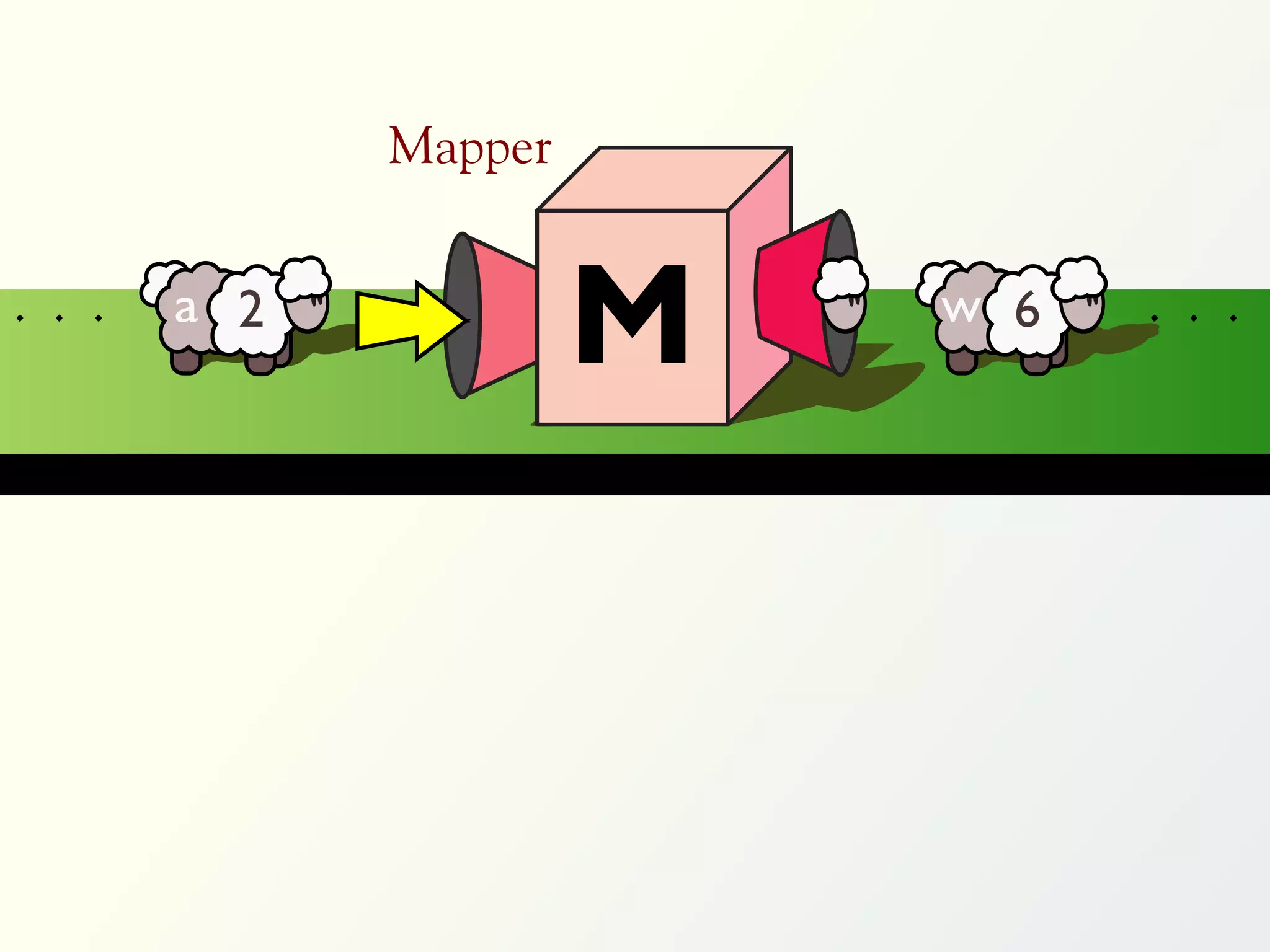
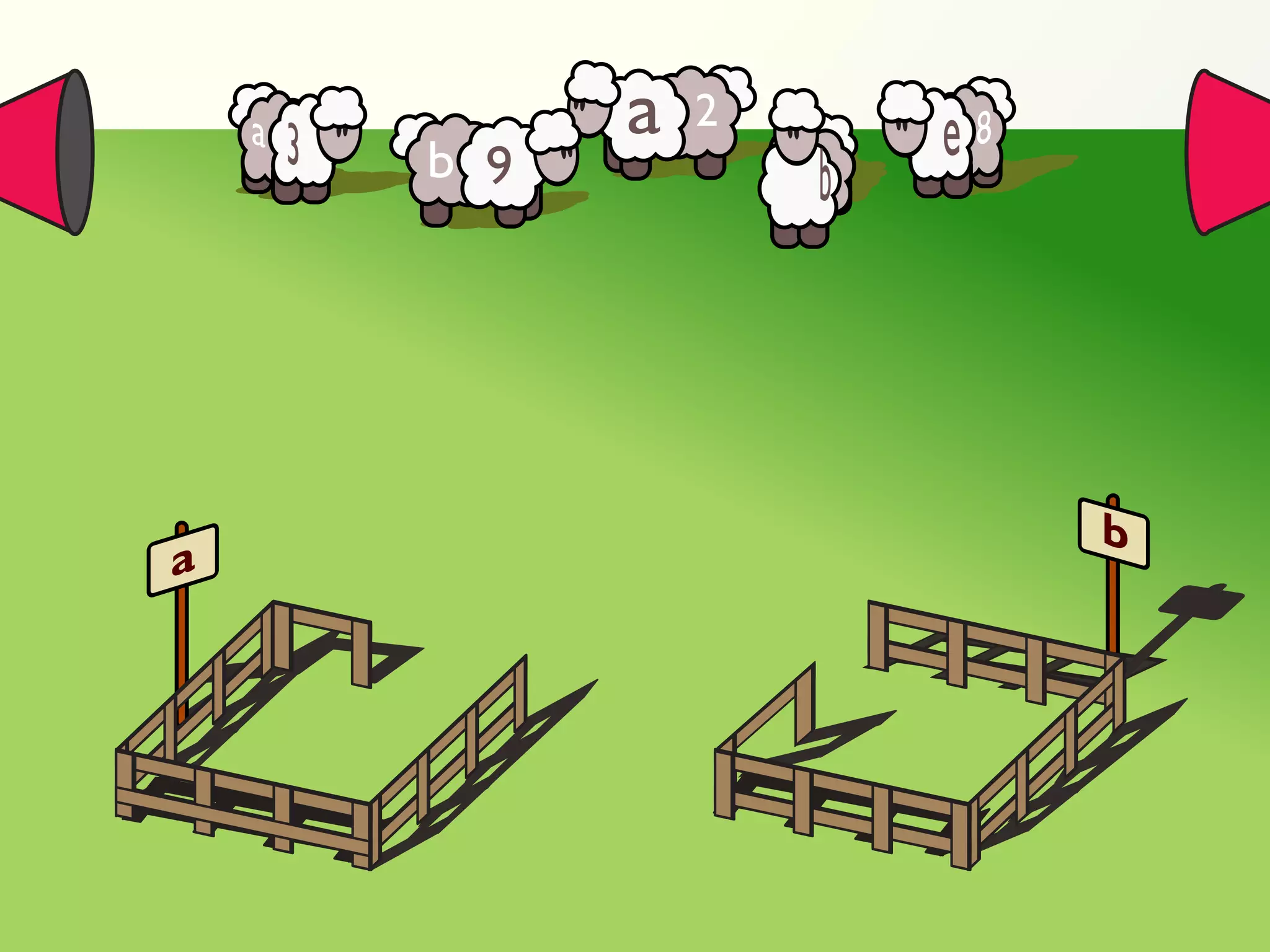
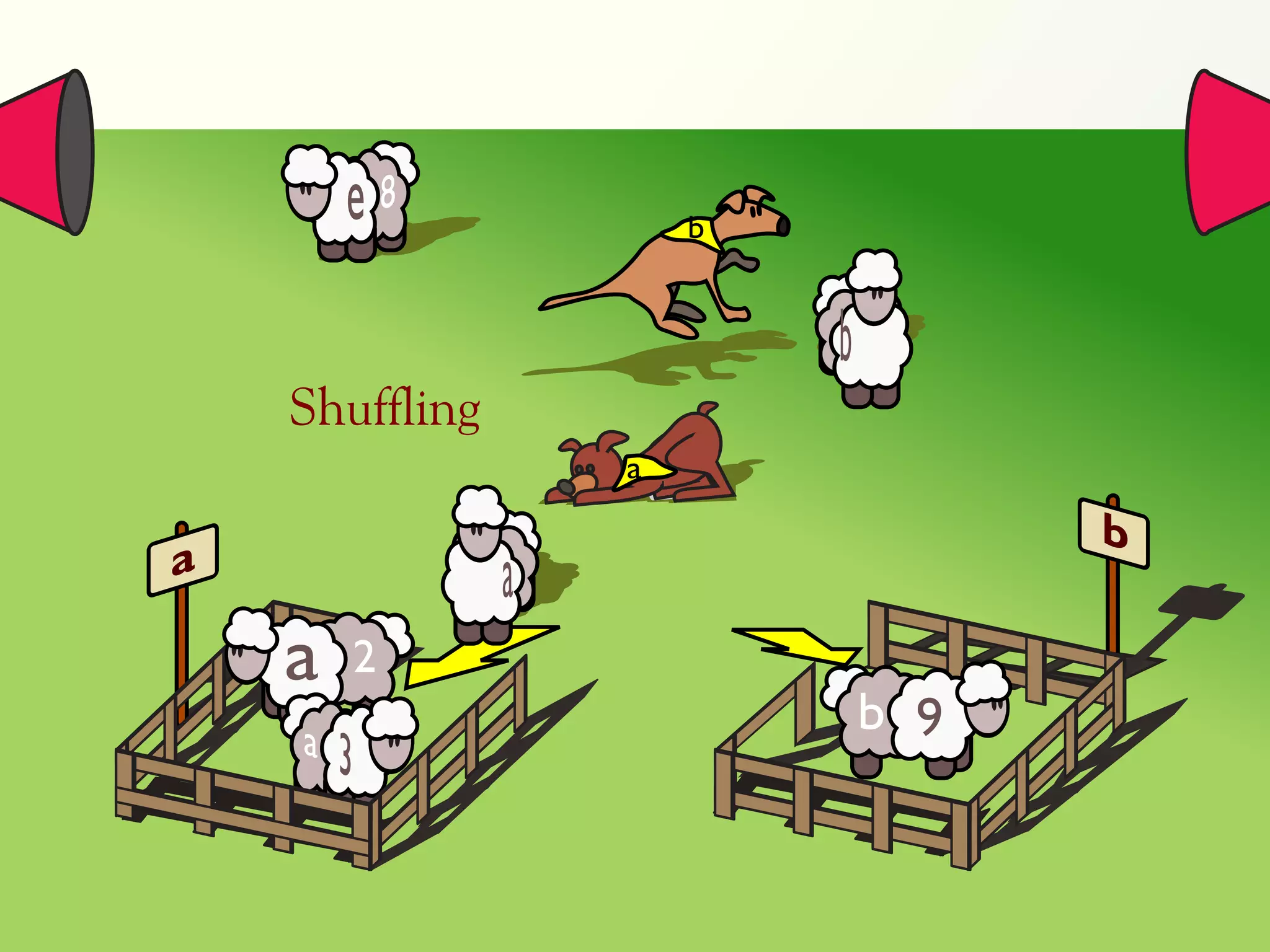
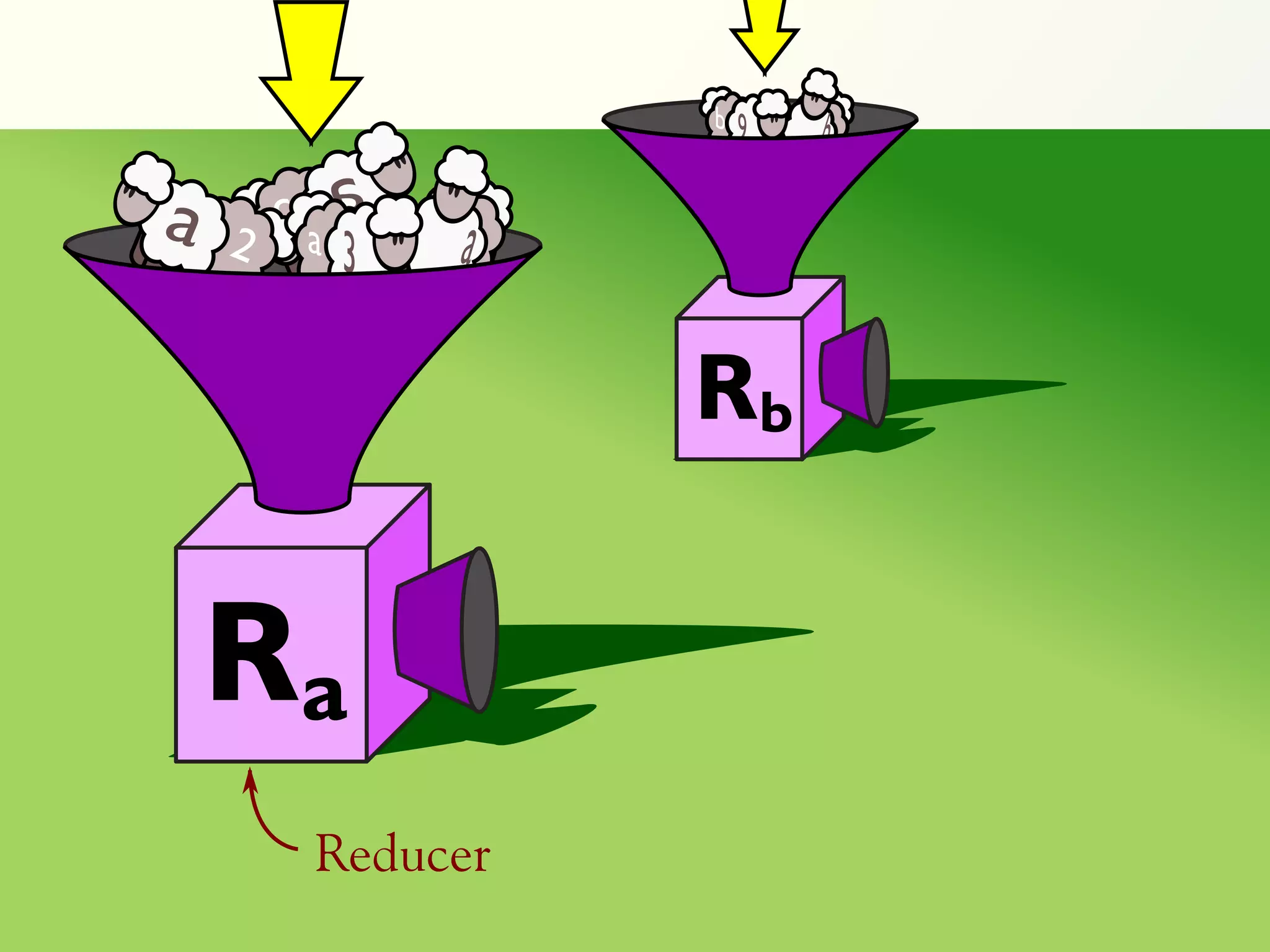
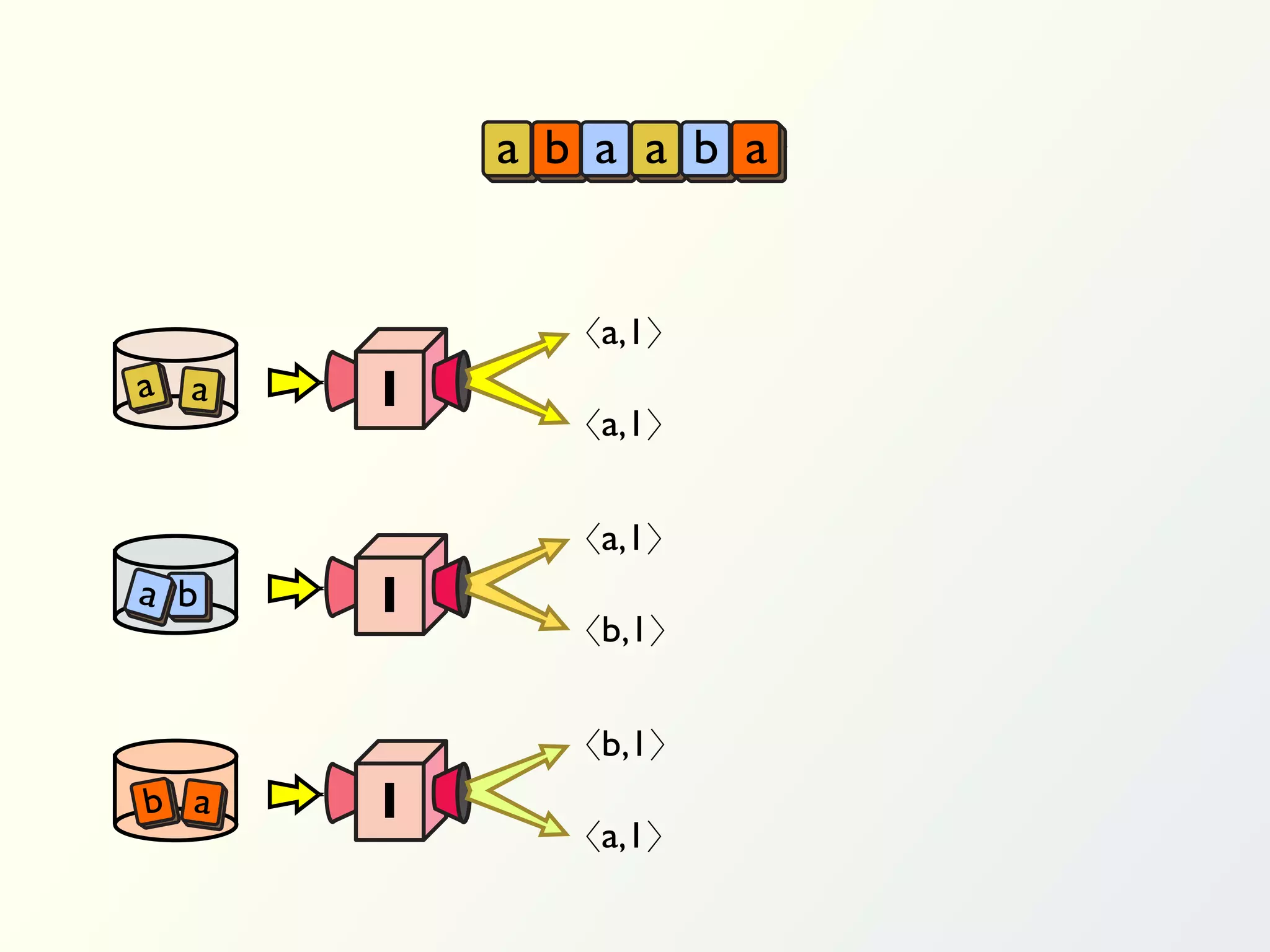
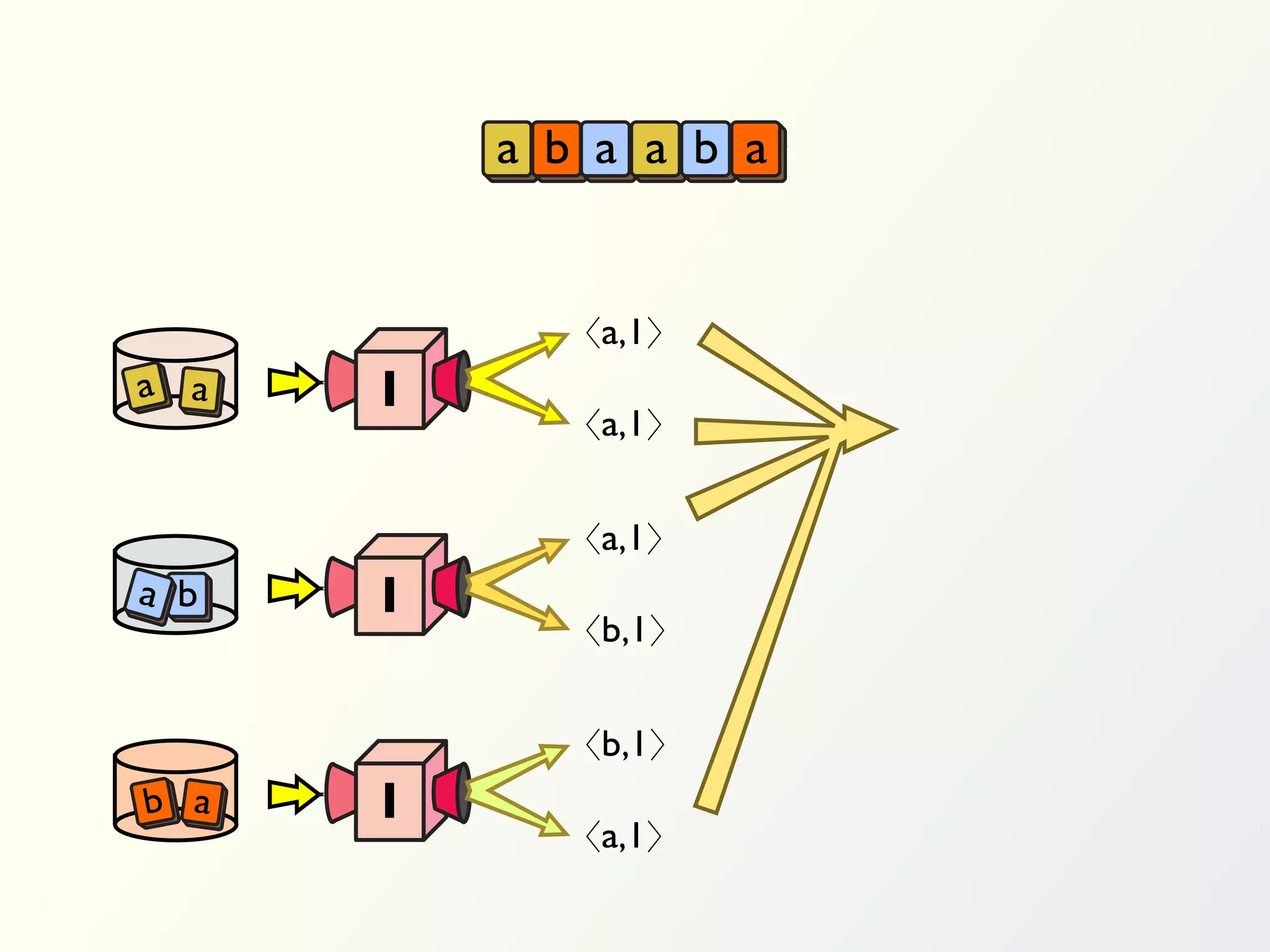
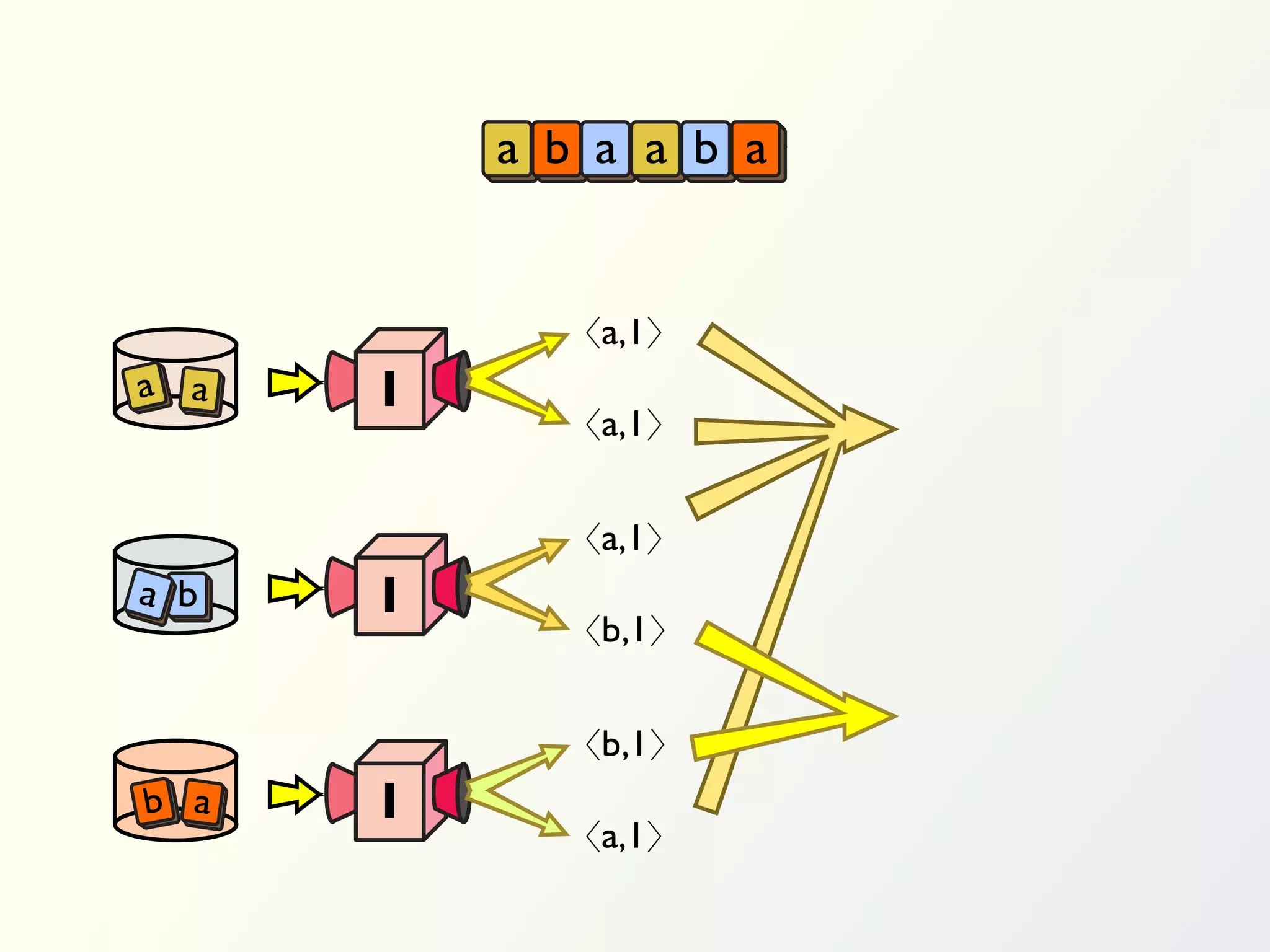
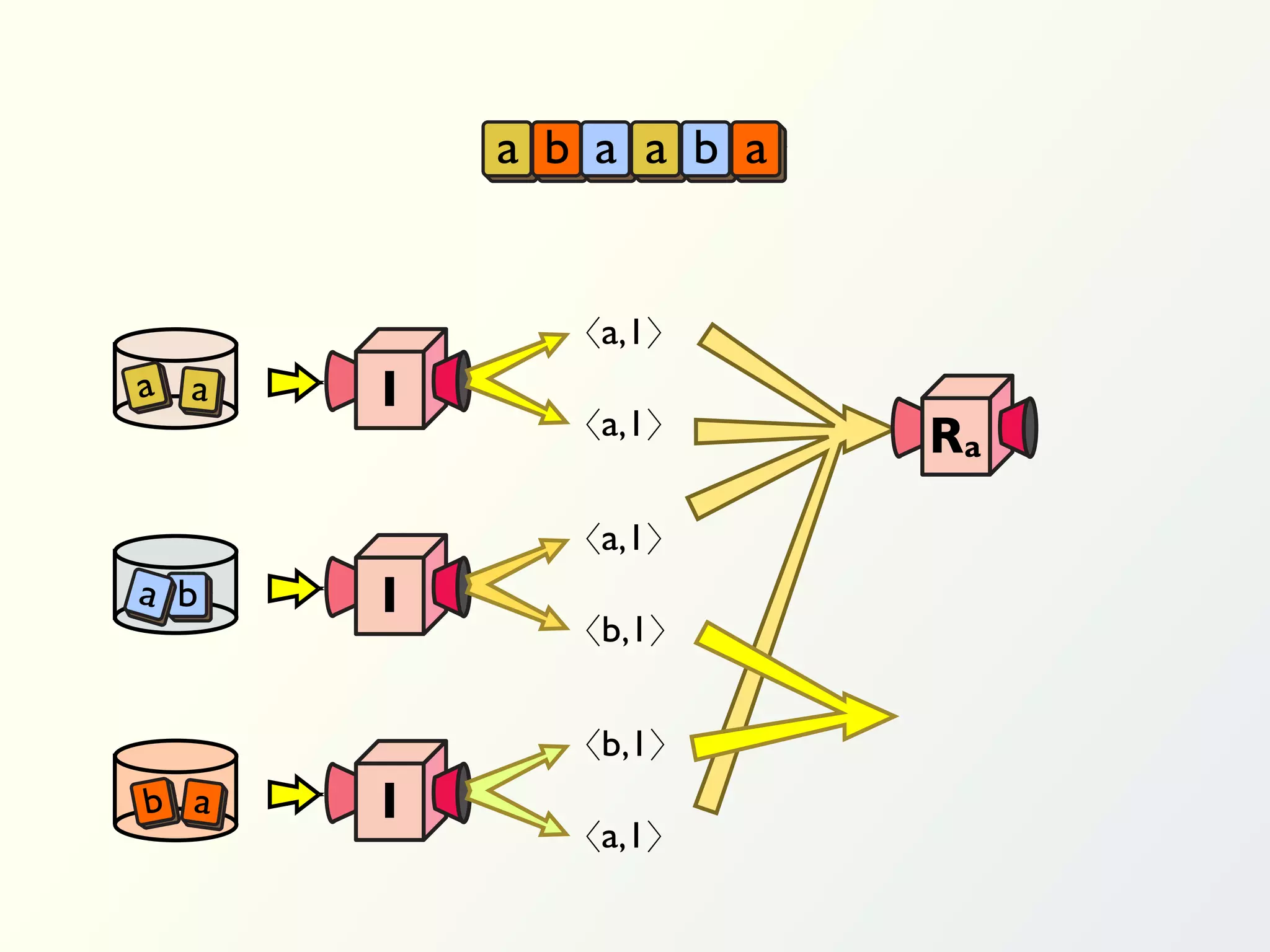
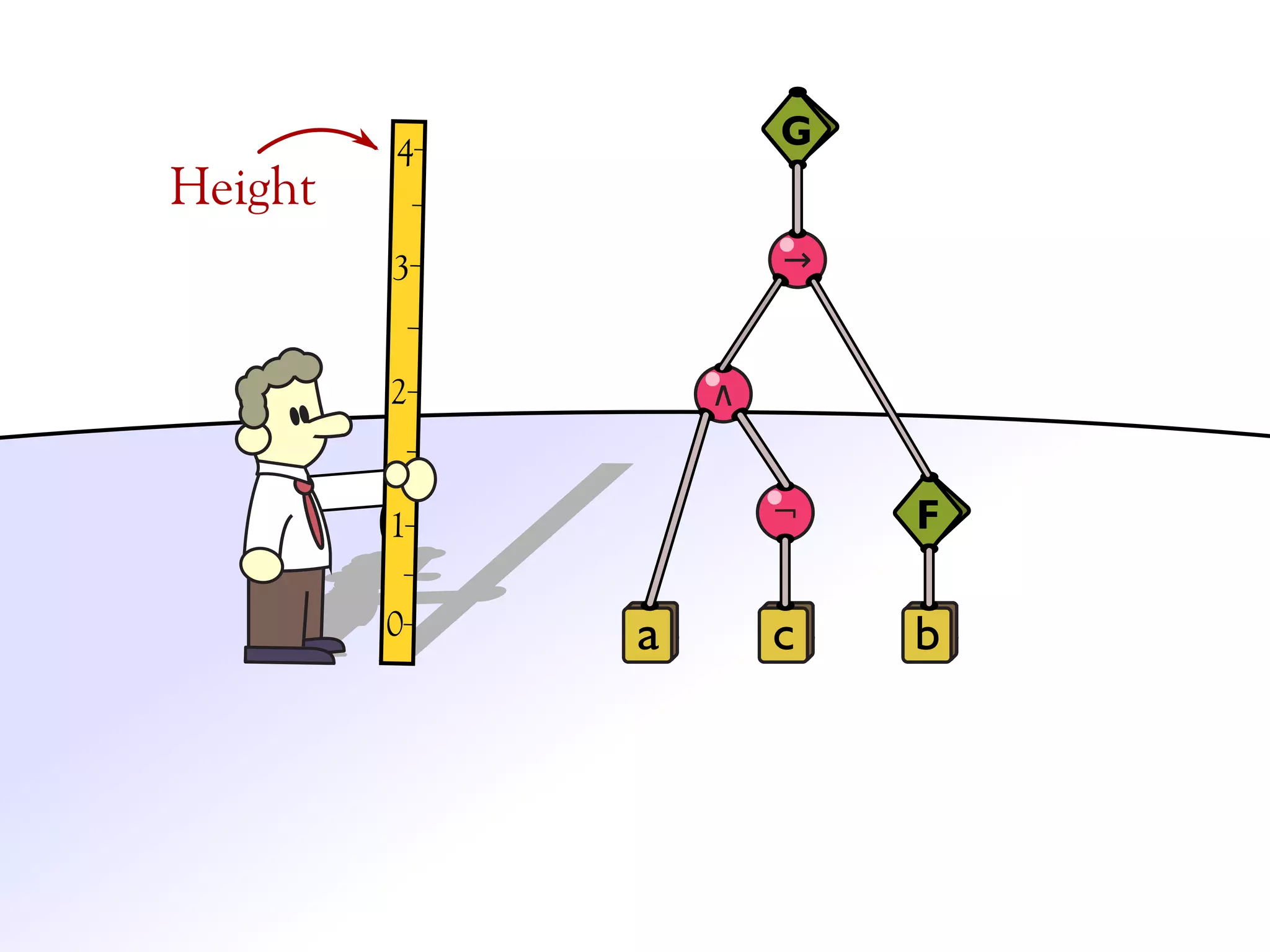
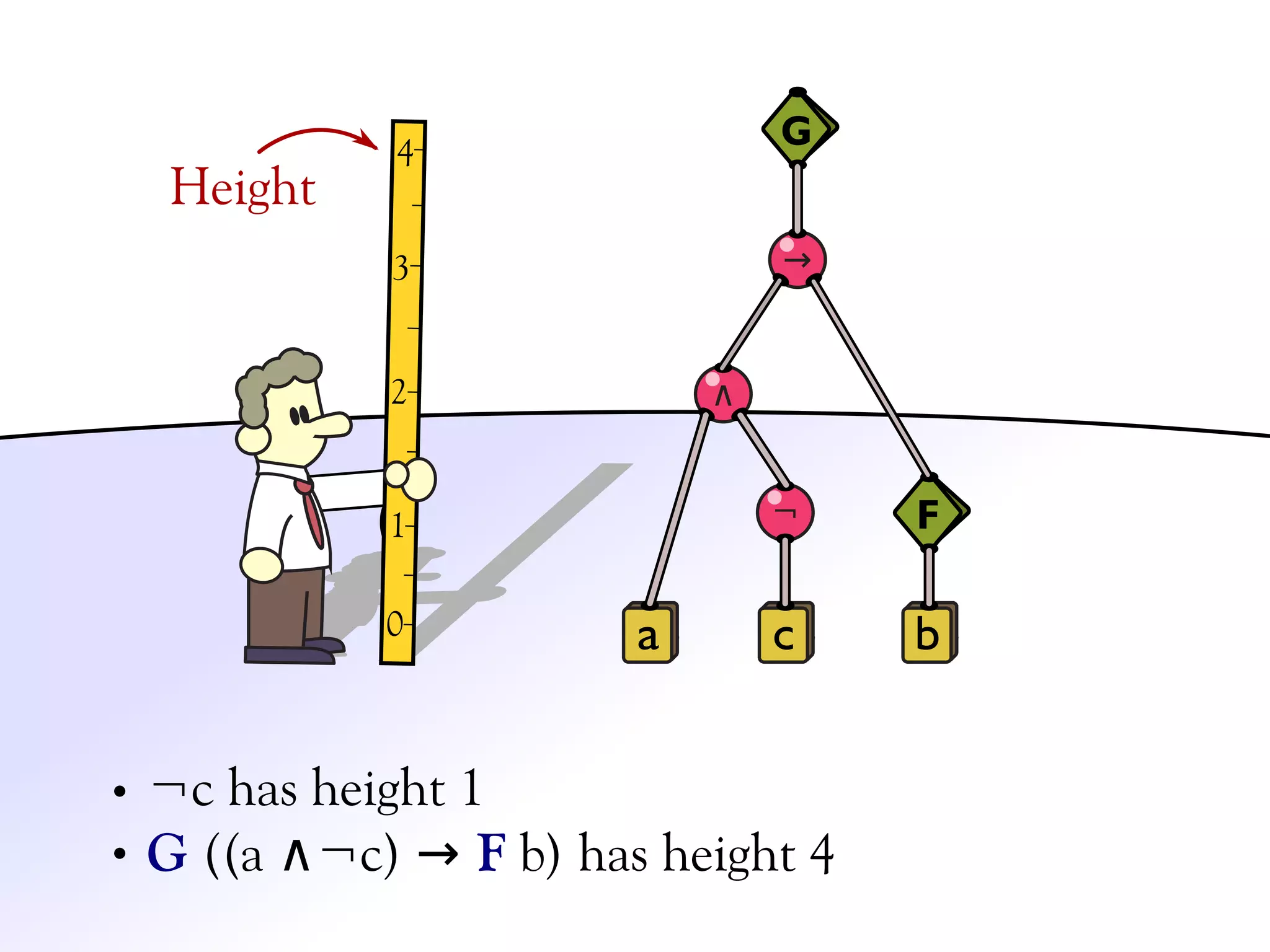
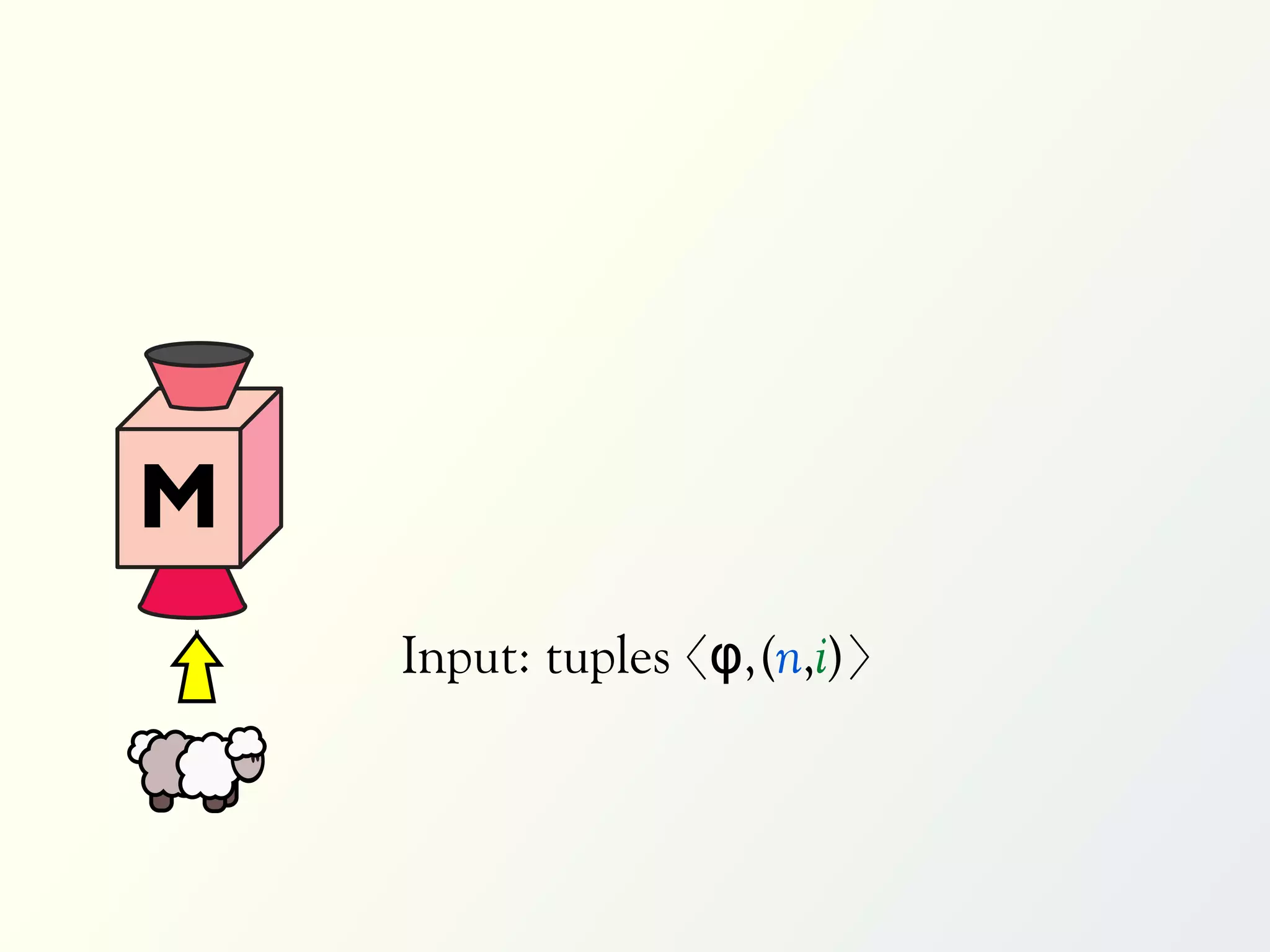
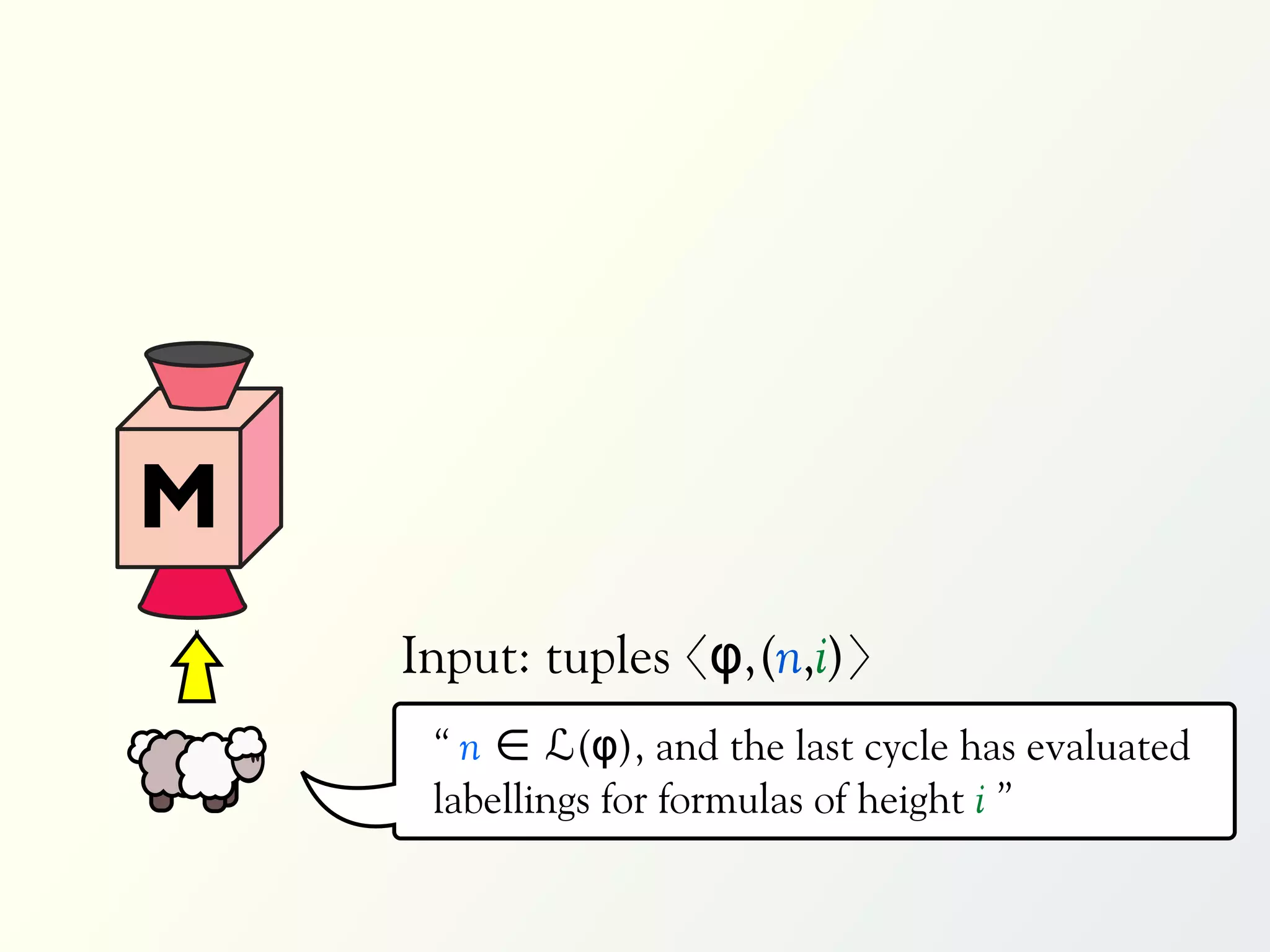
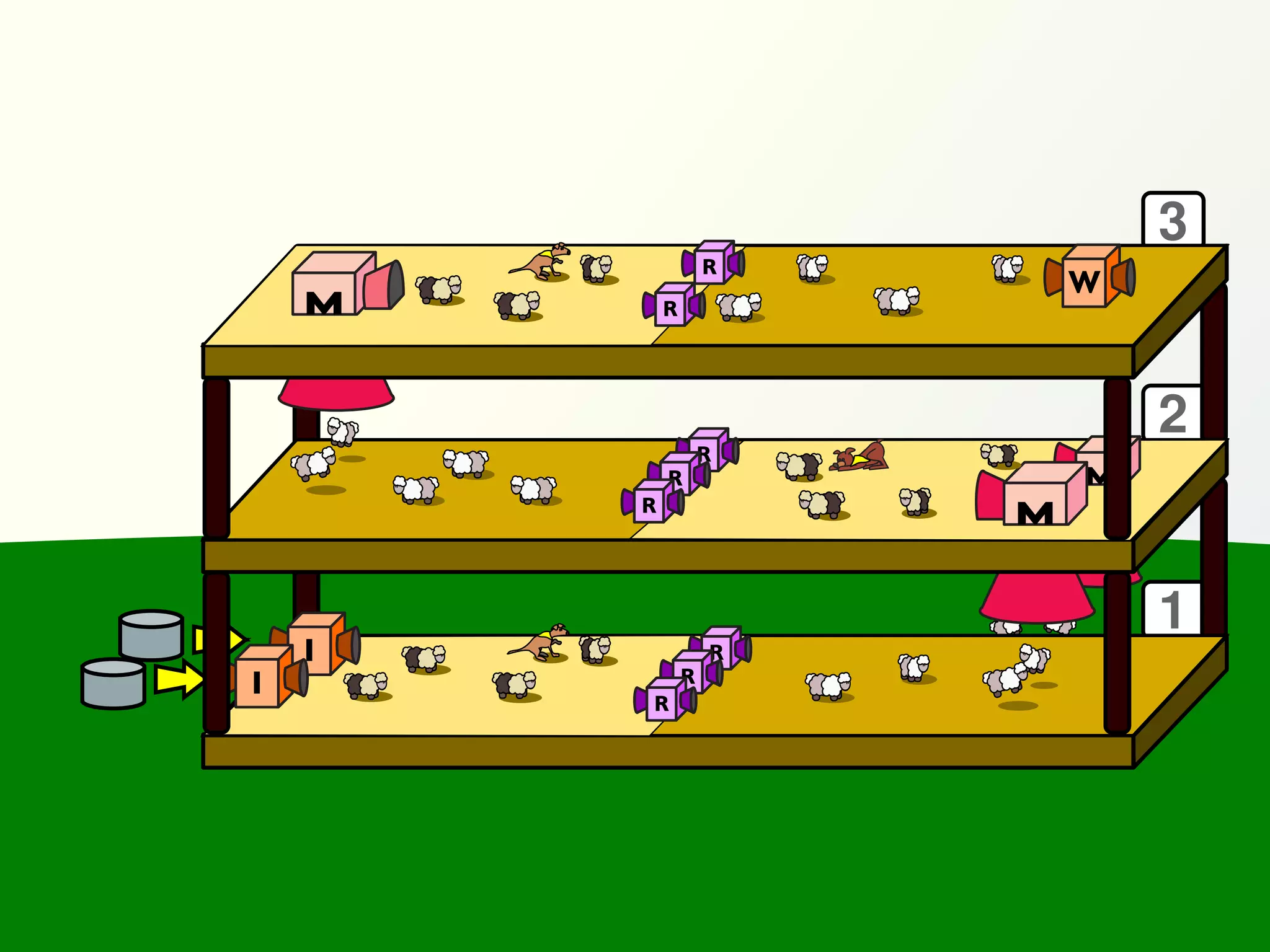
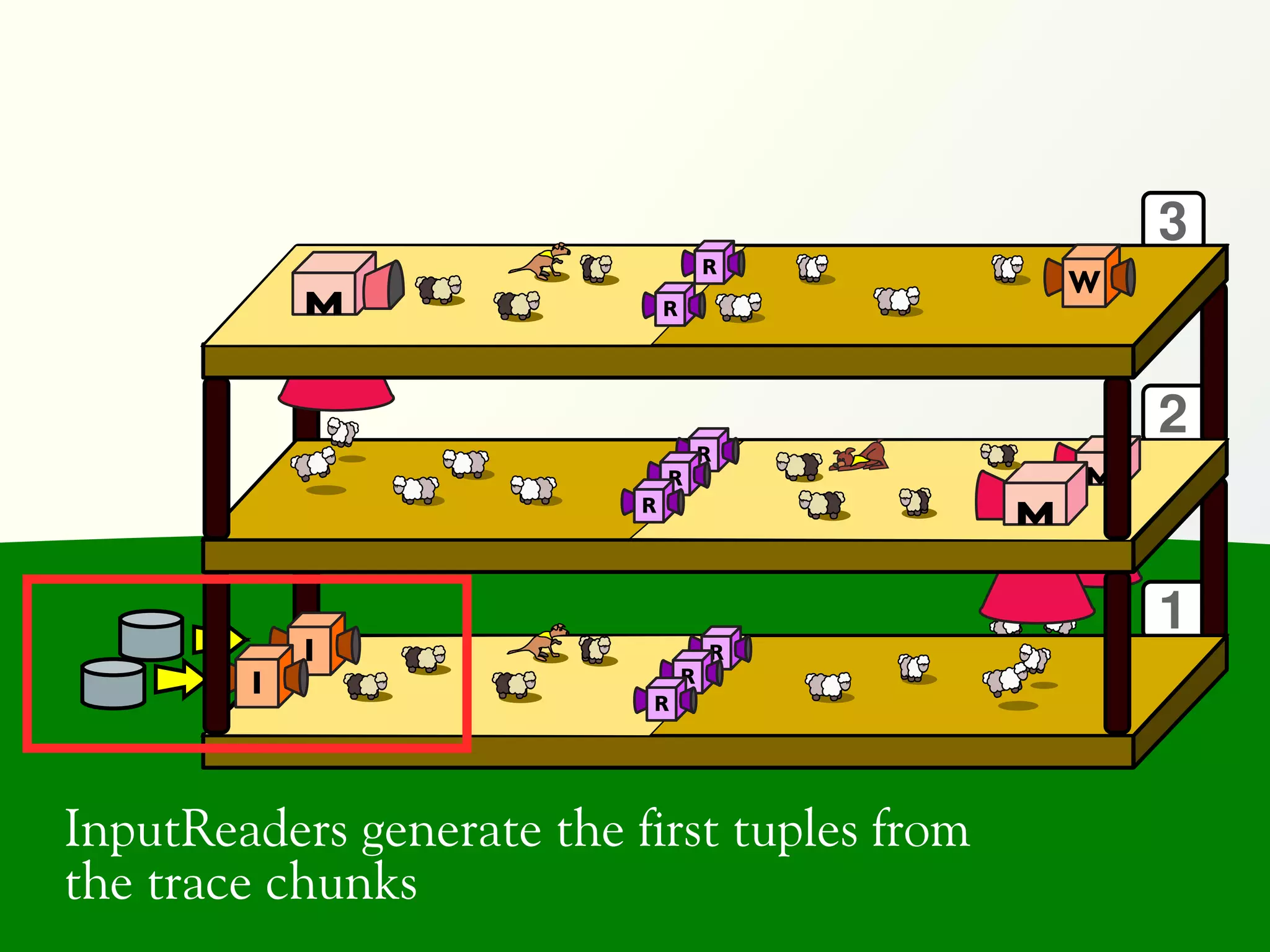
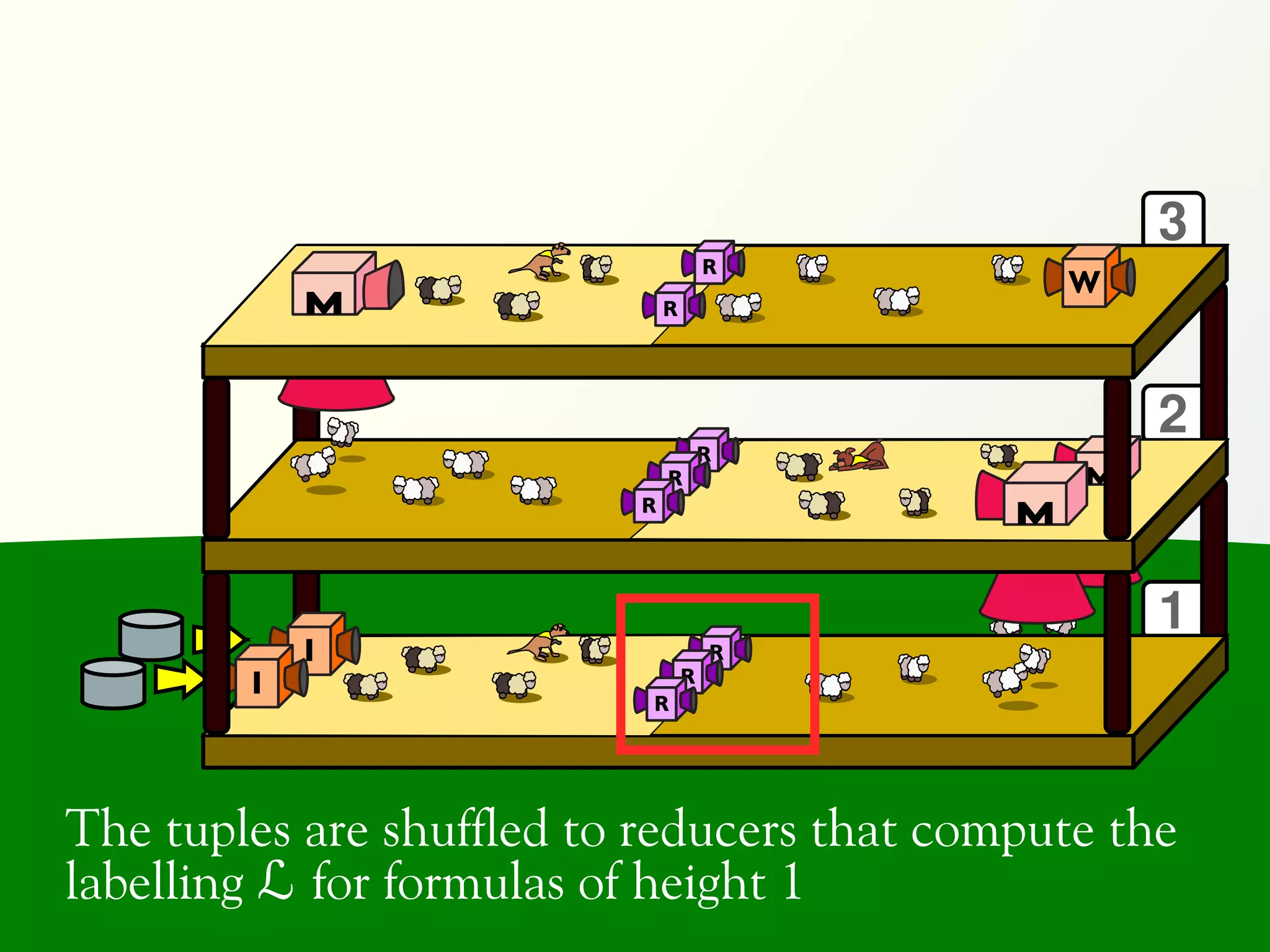
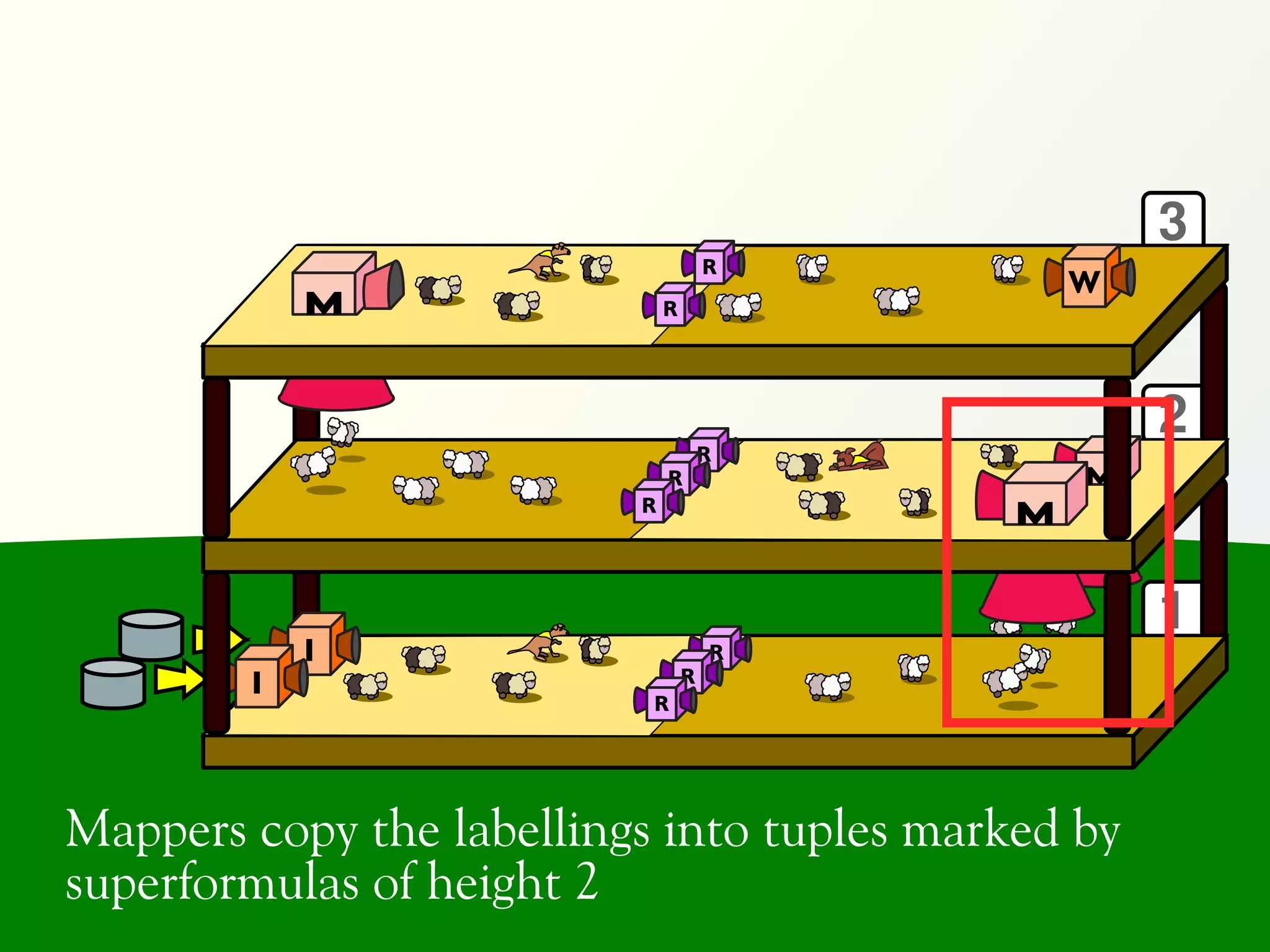
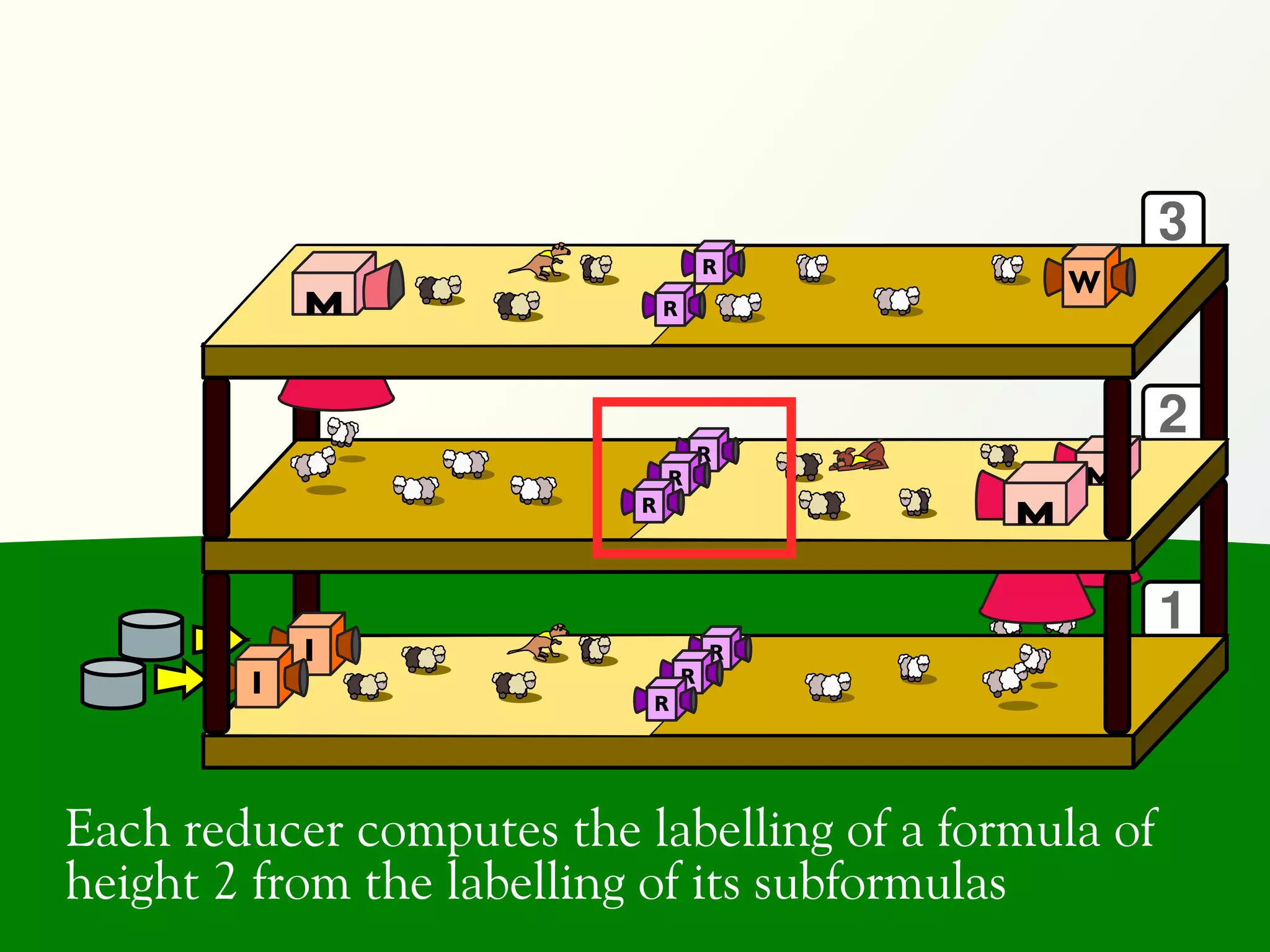
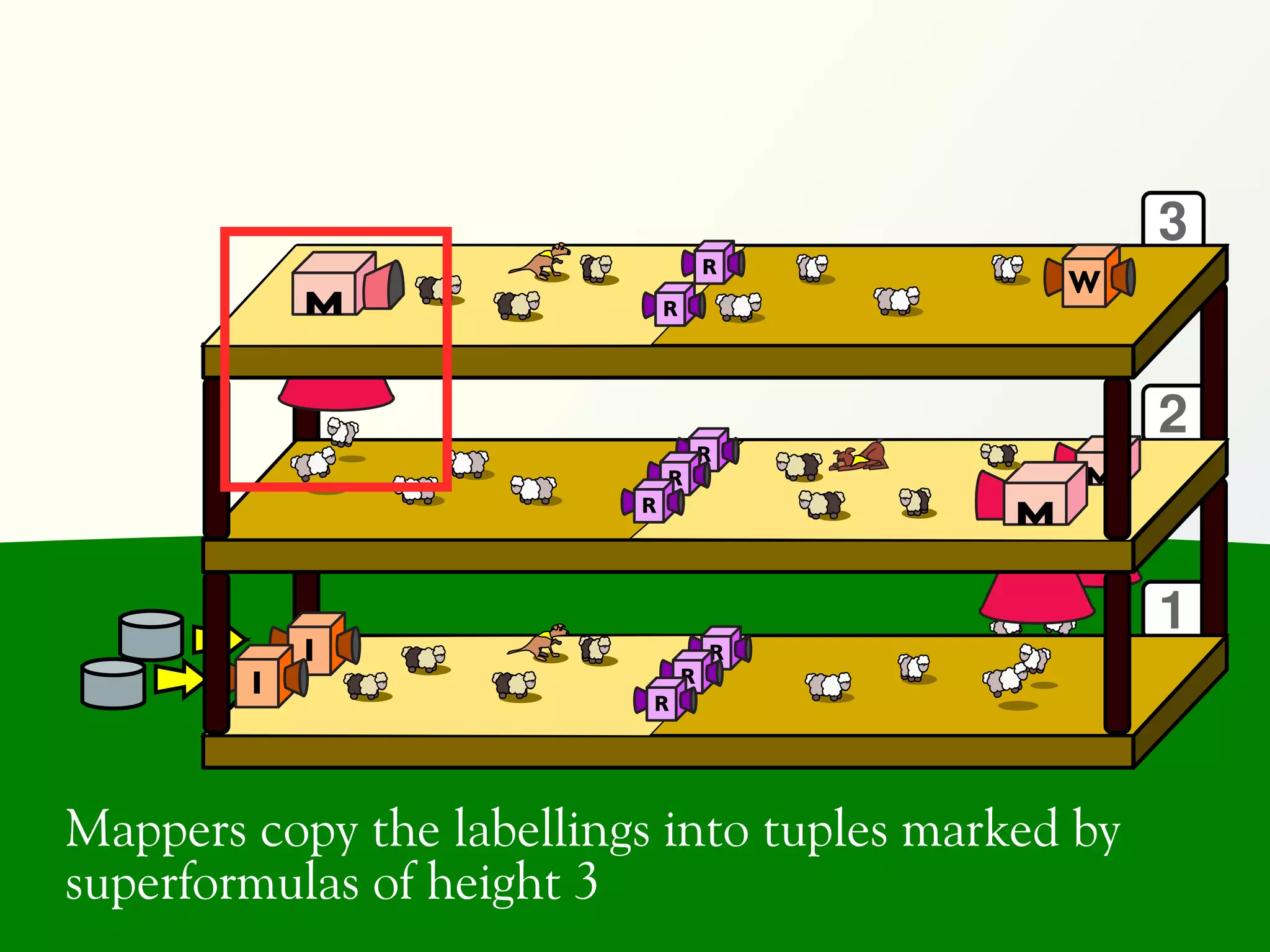
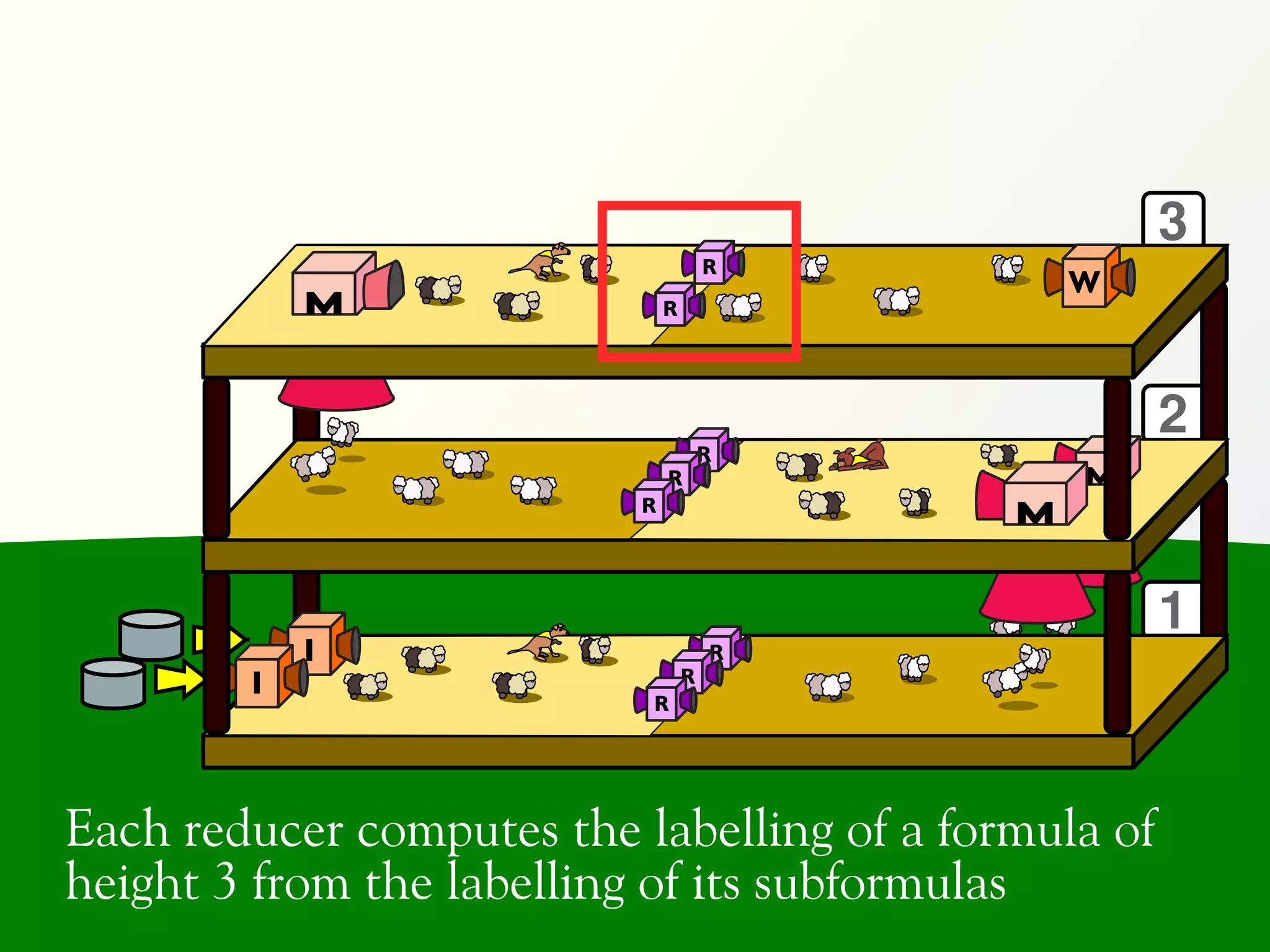
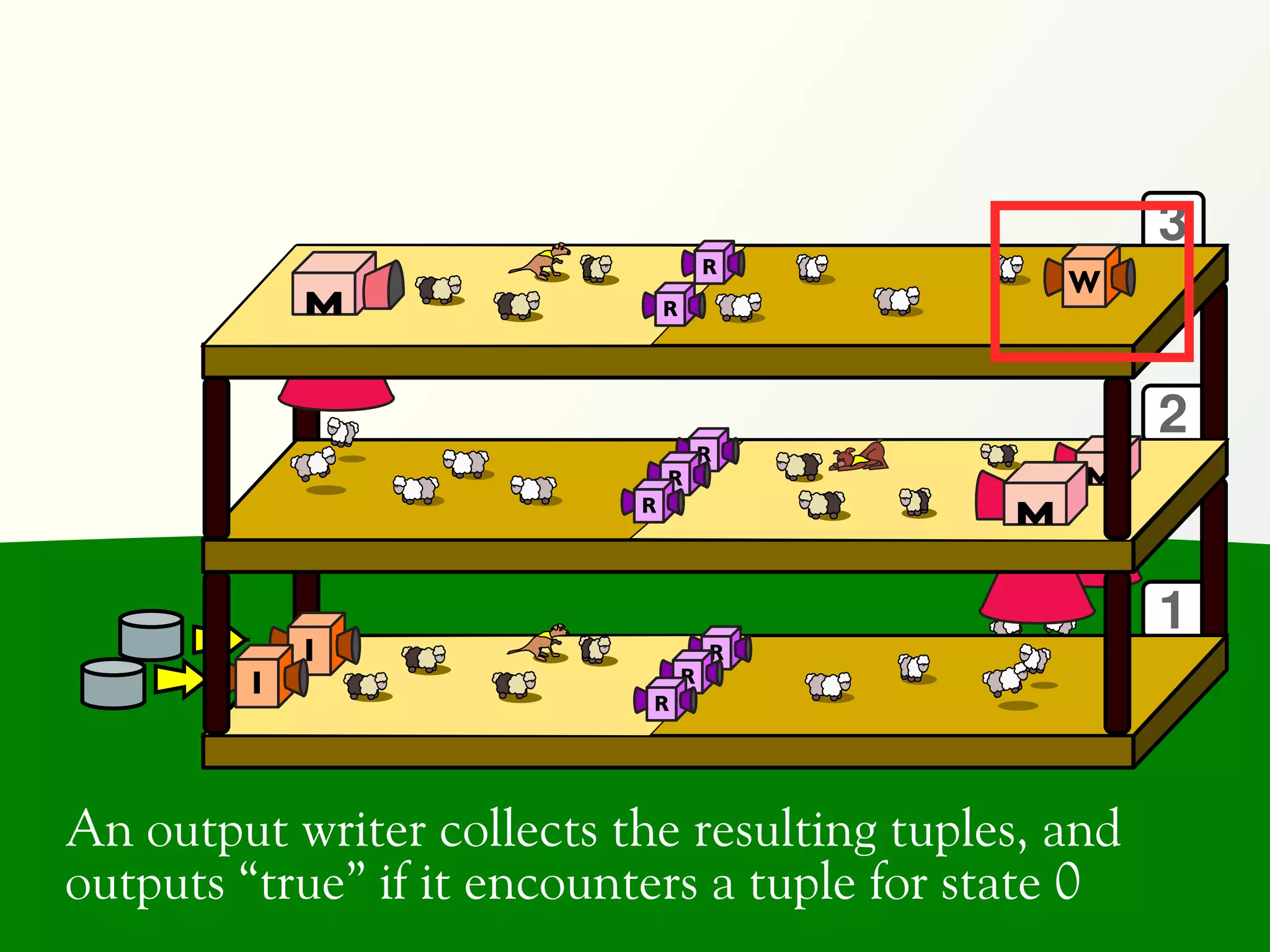
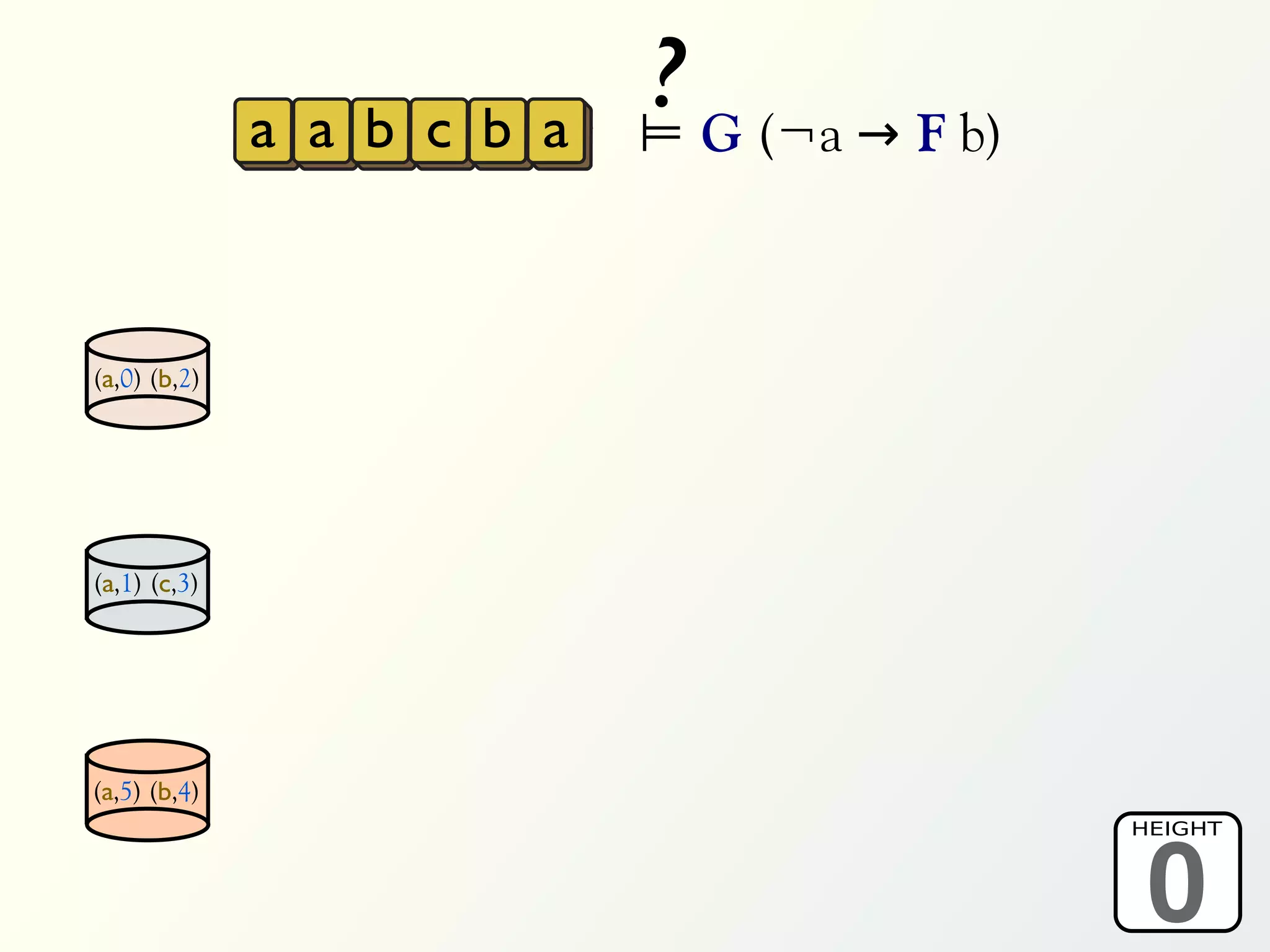
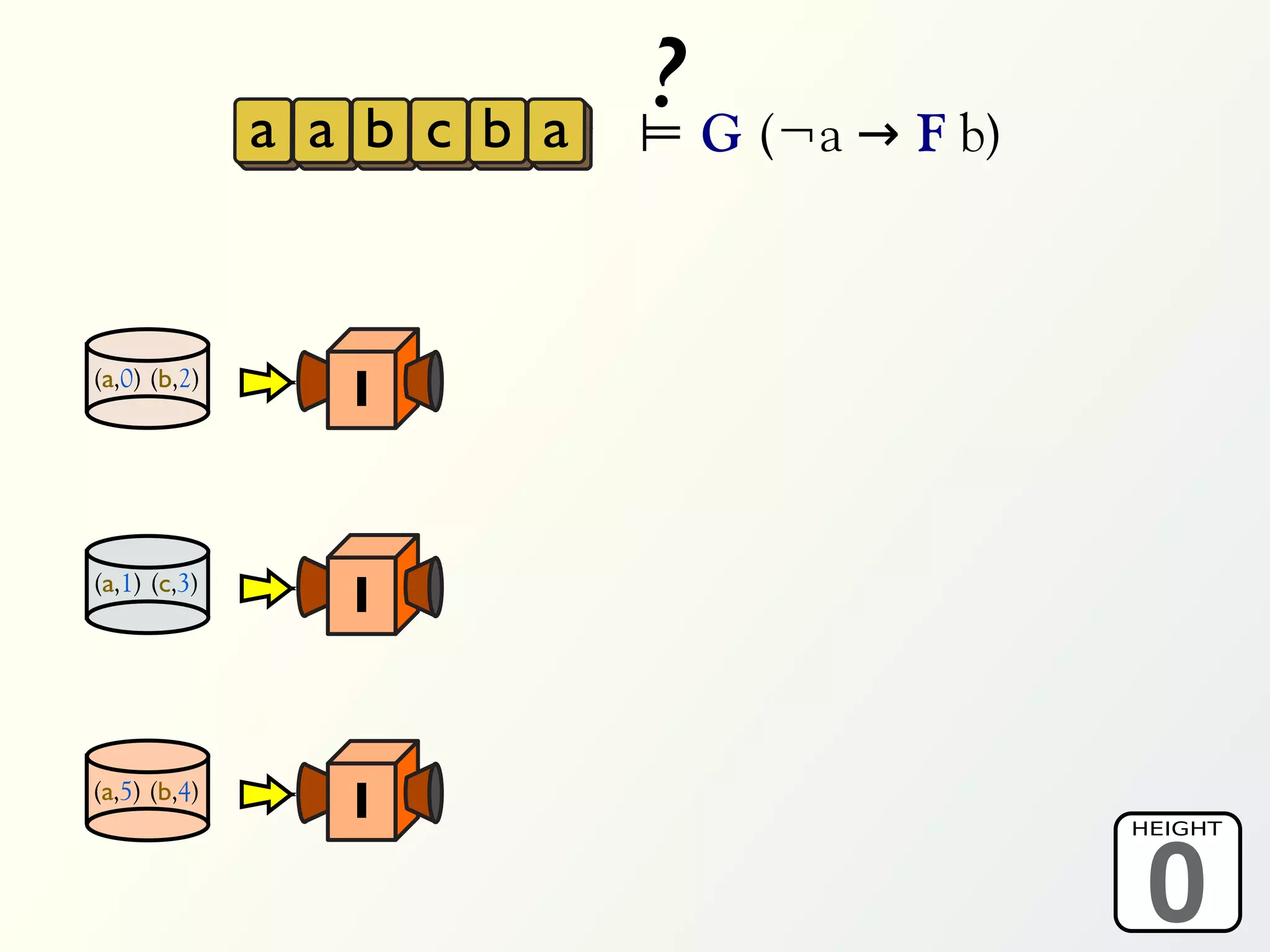
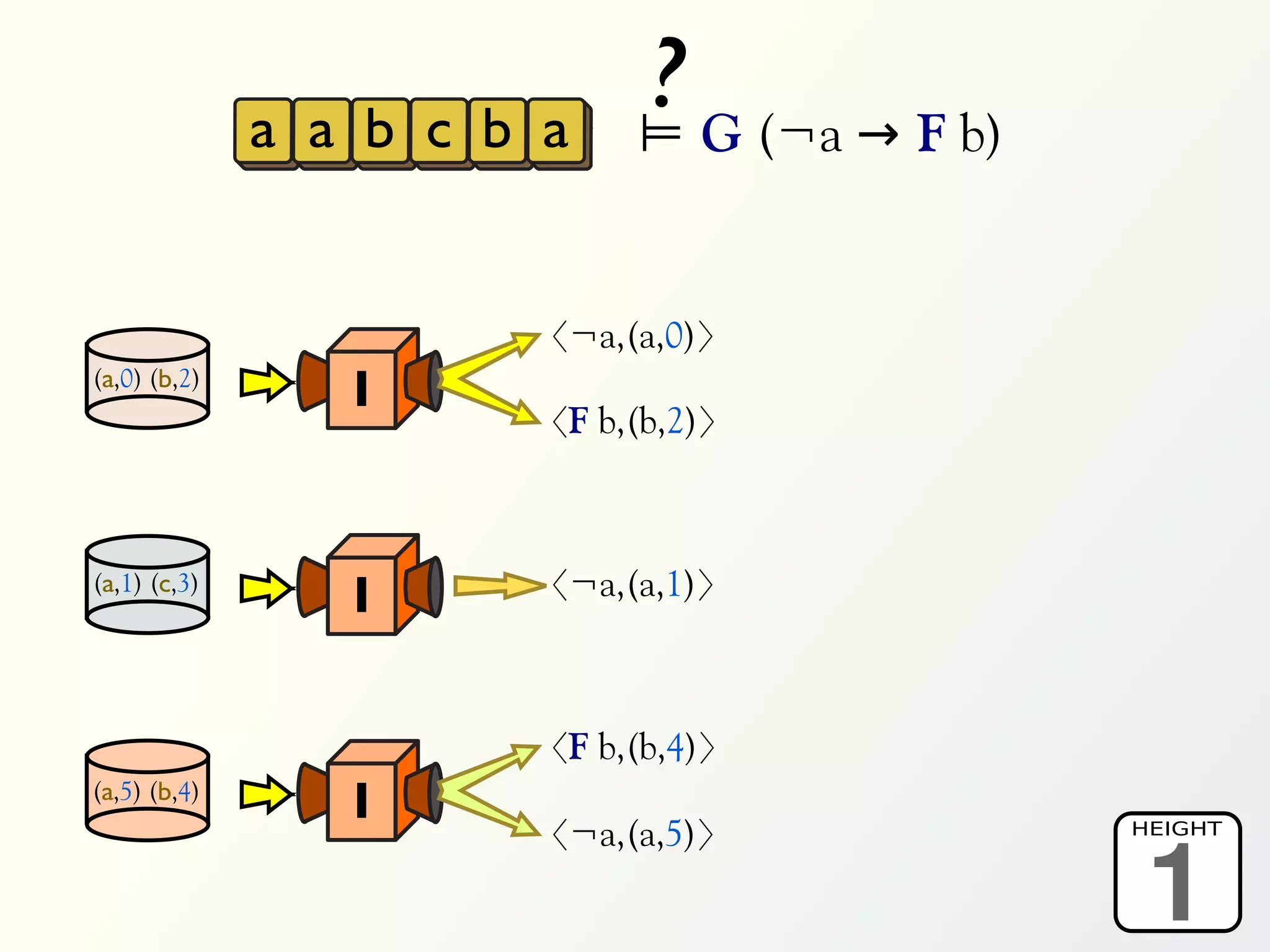
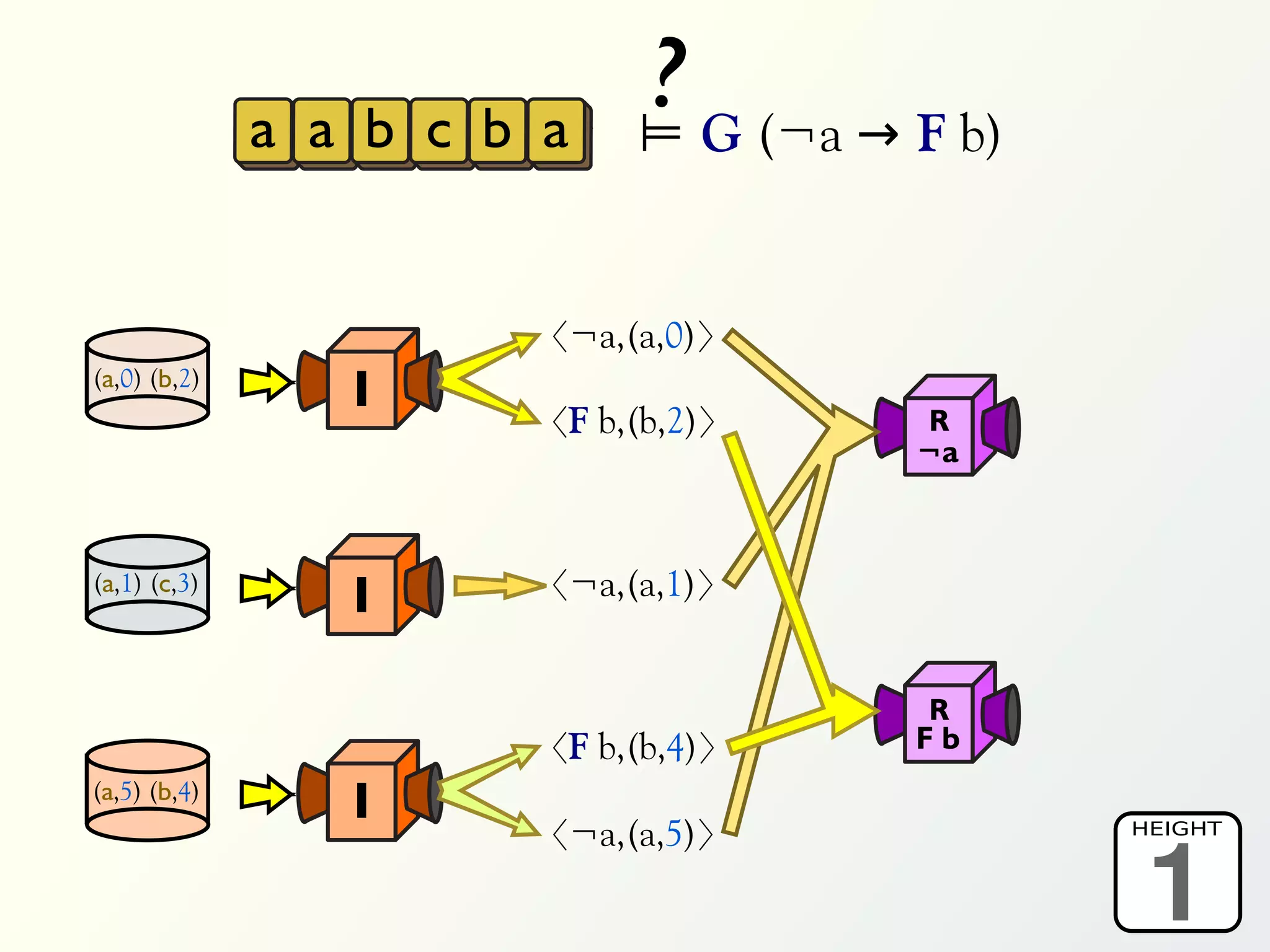
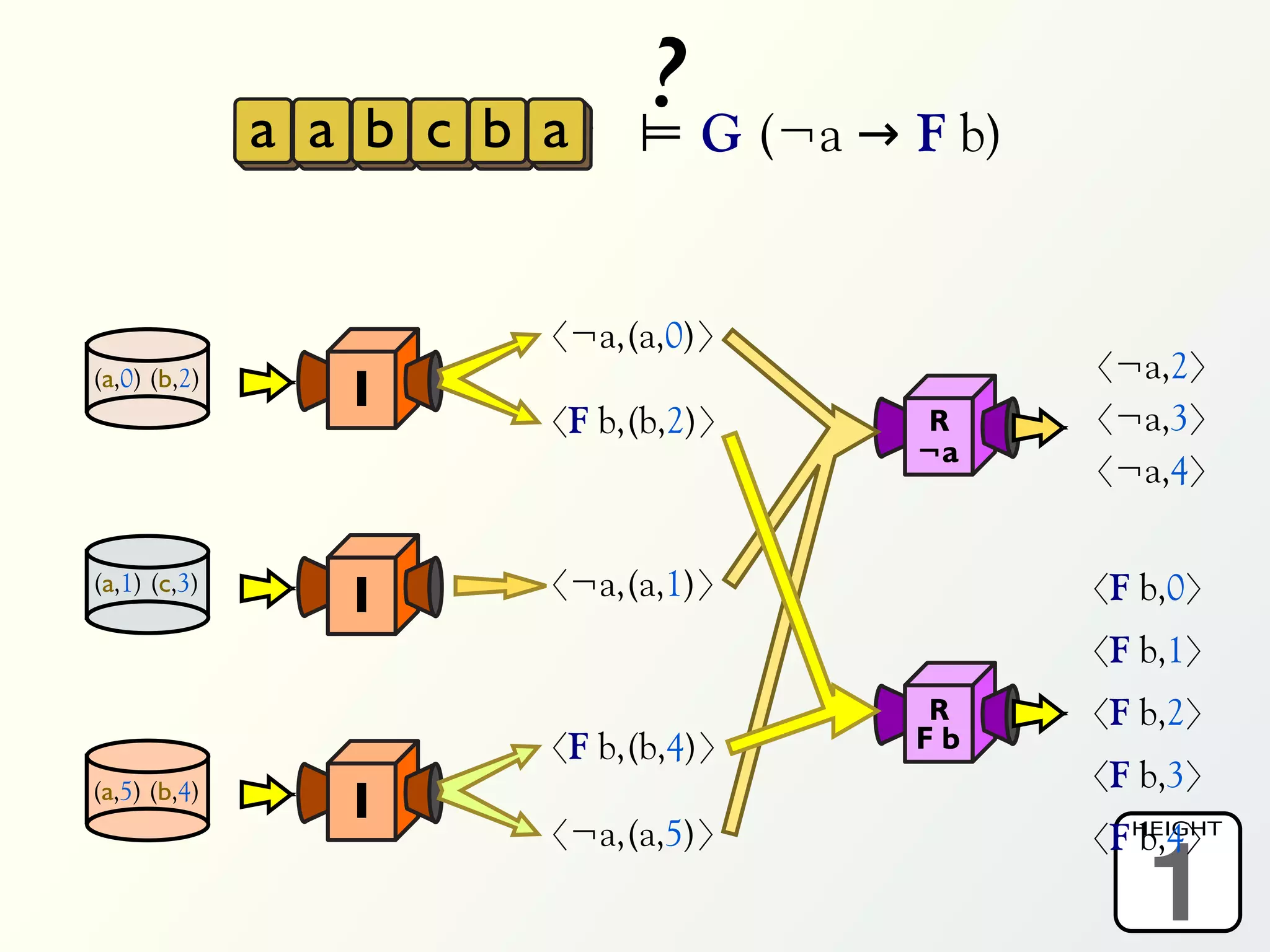
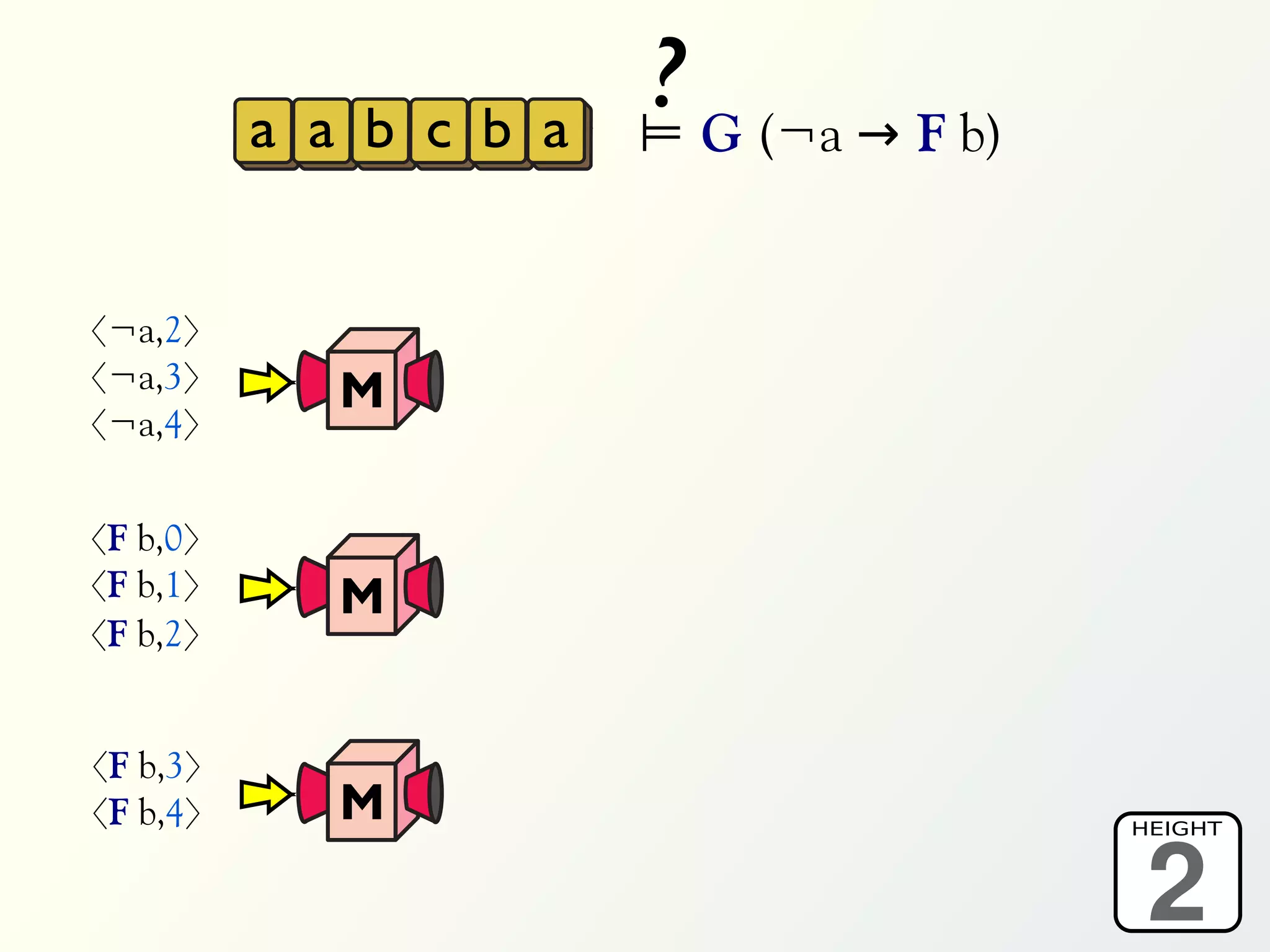
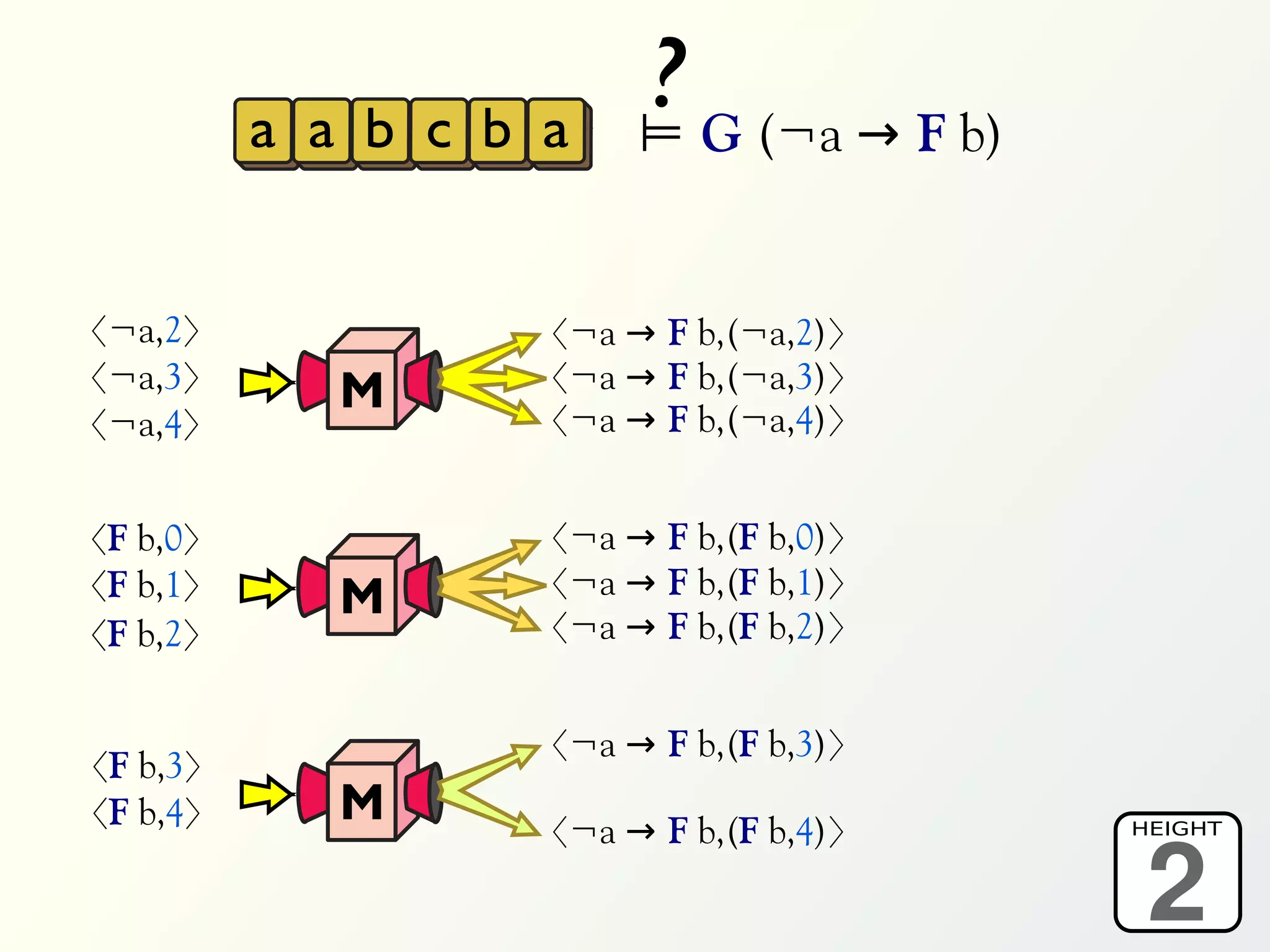
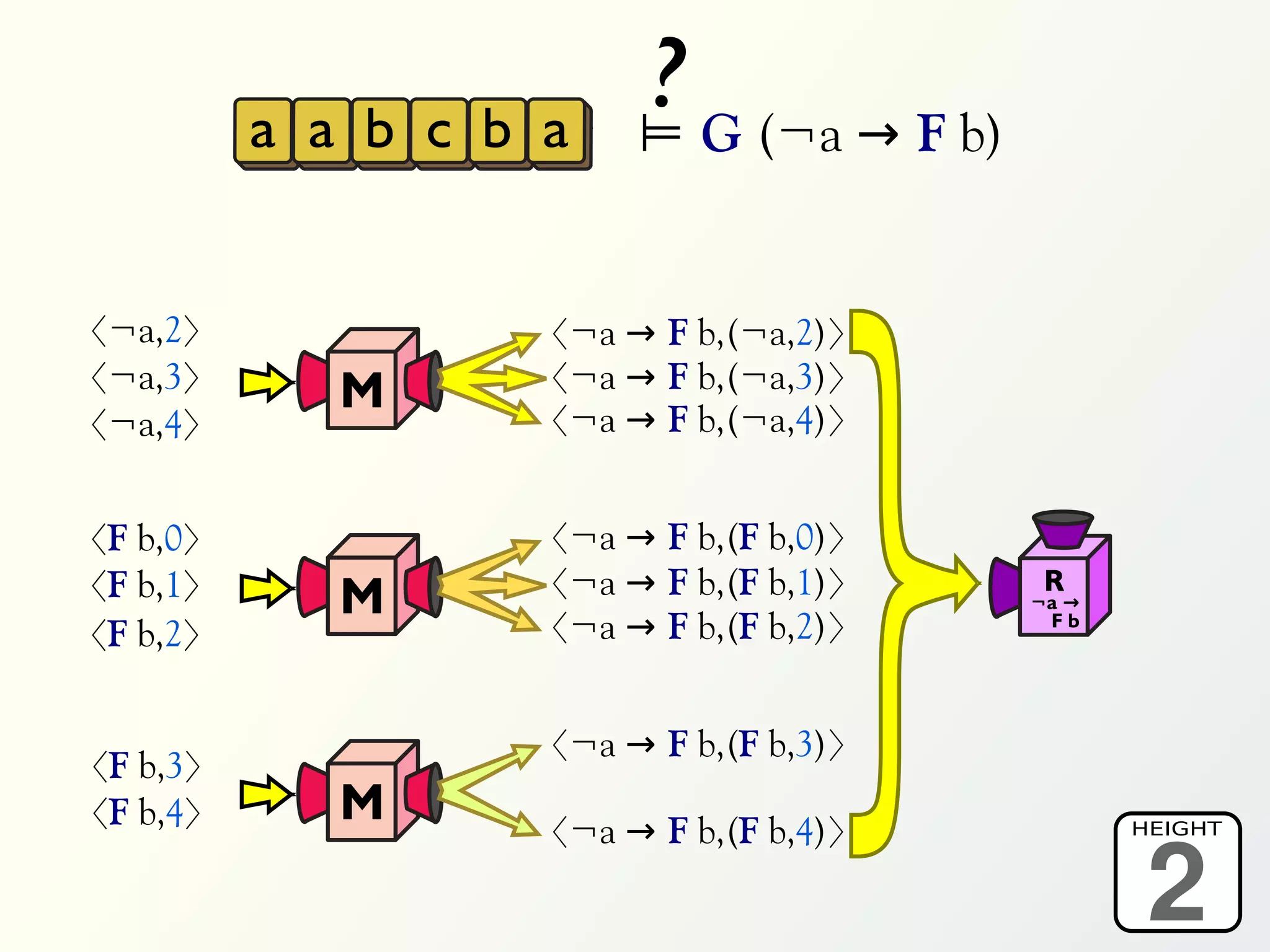
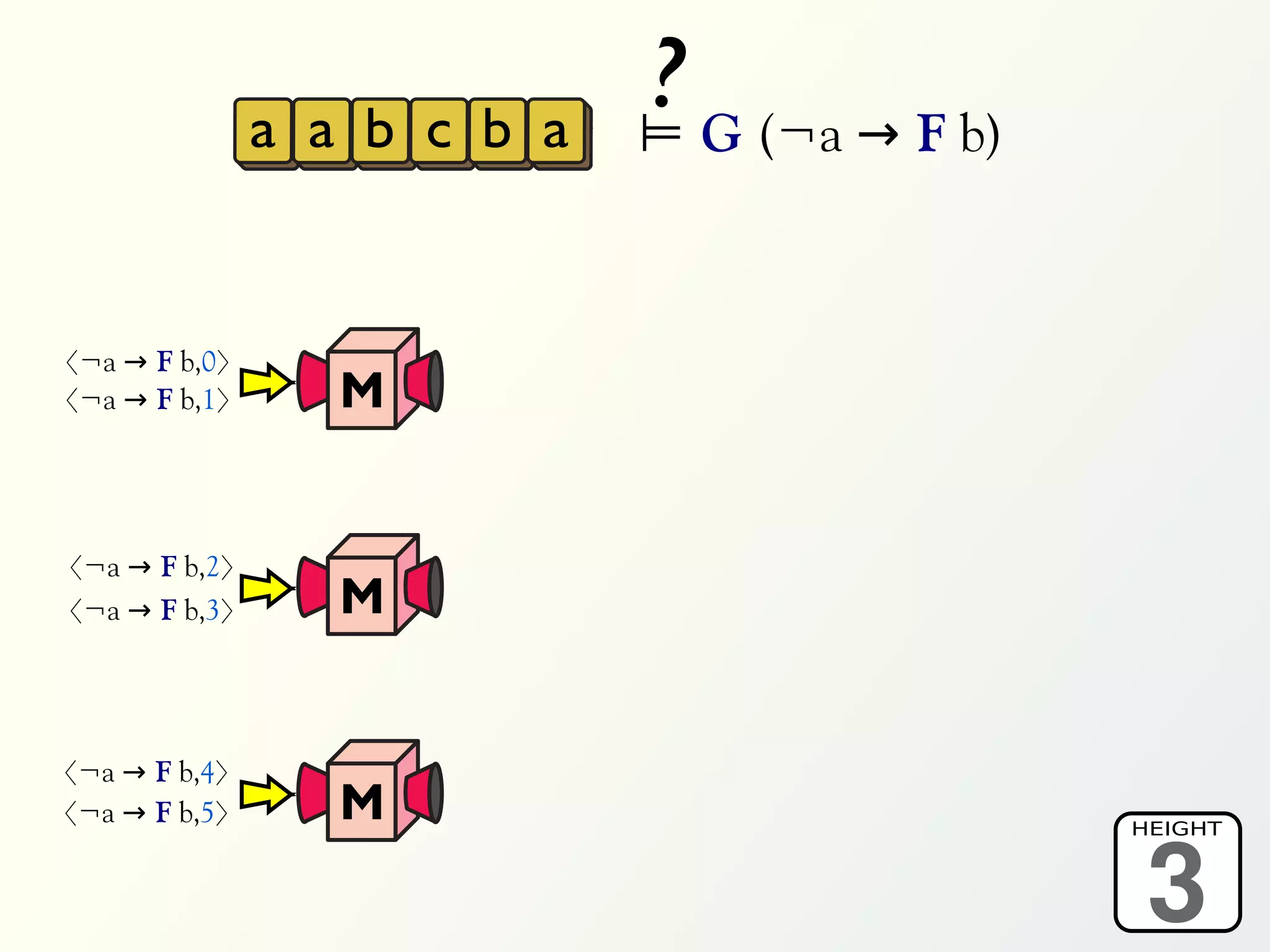
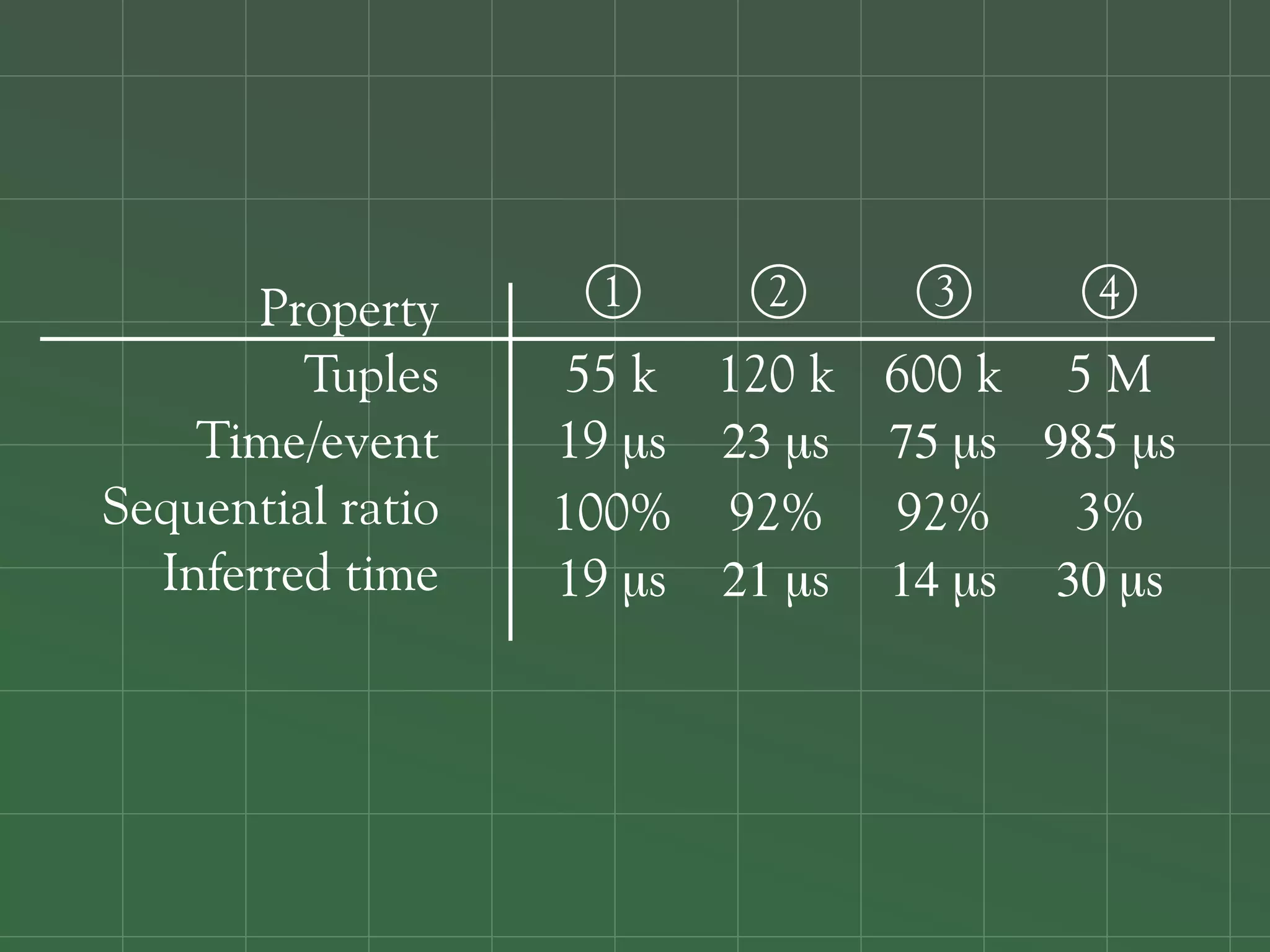
118. Validation of 4 LTL formulas:
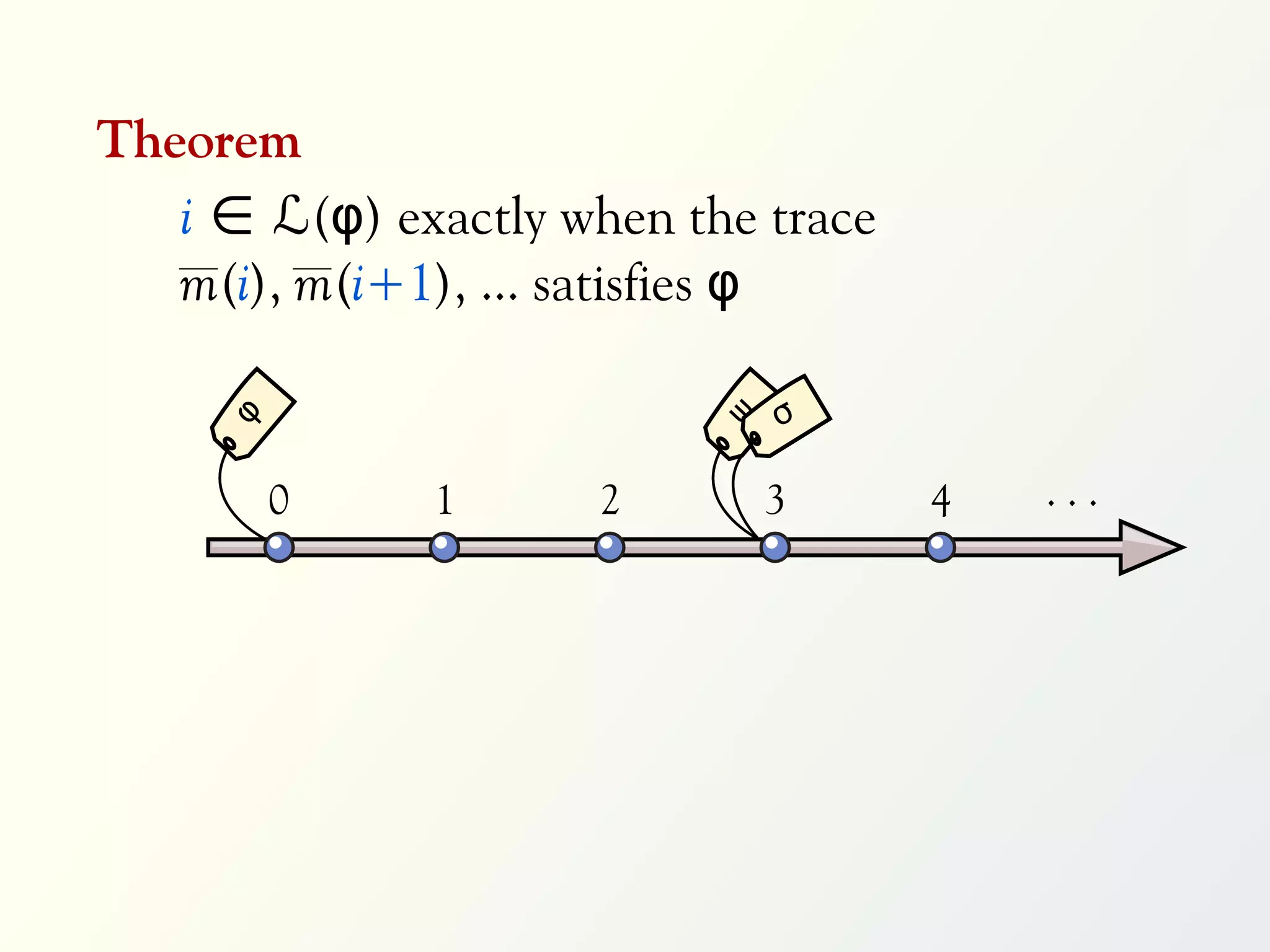
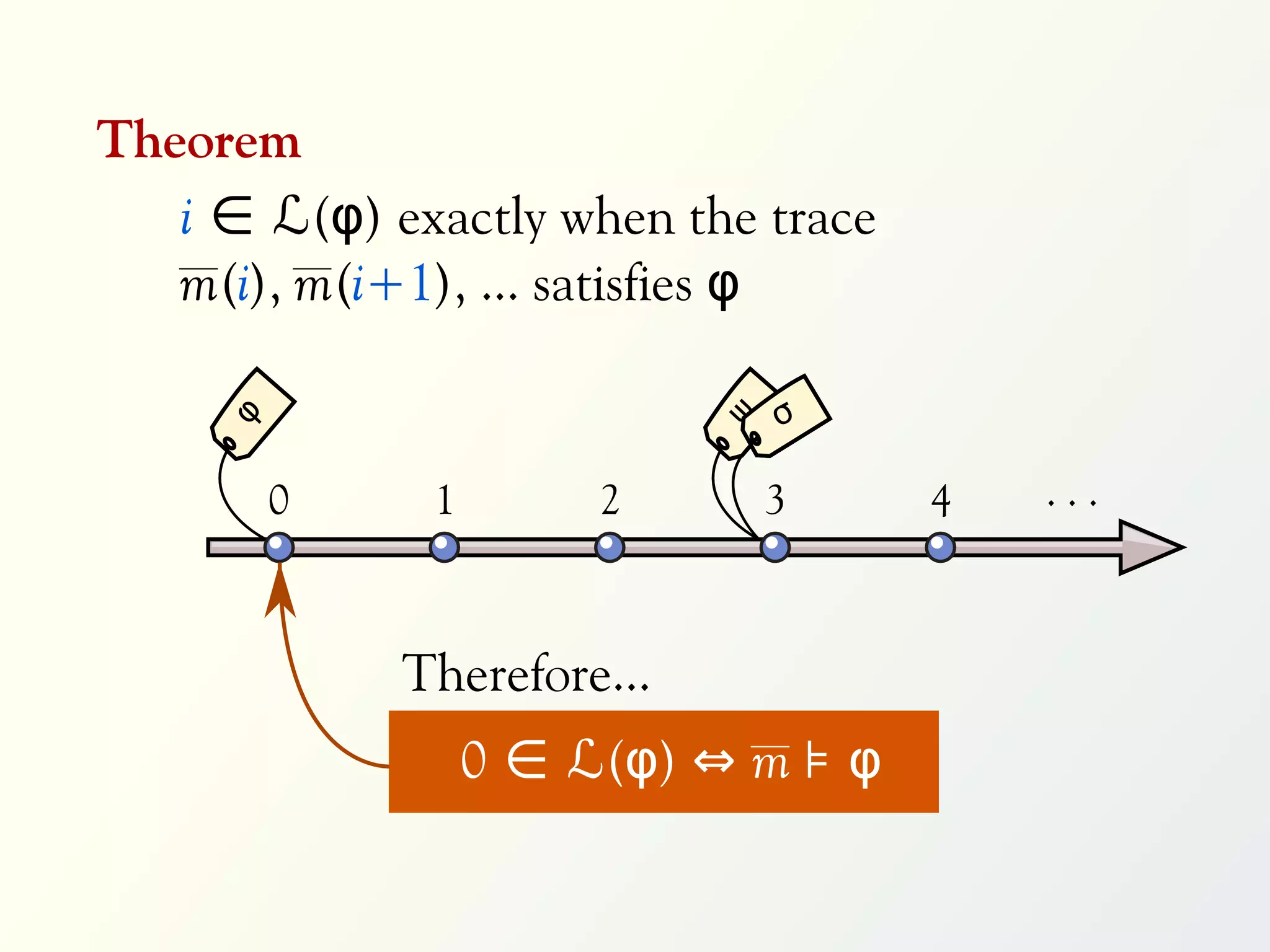
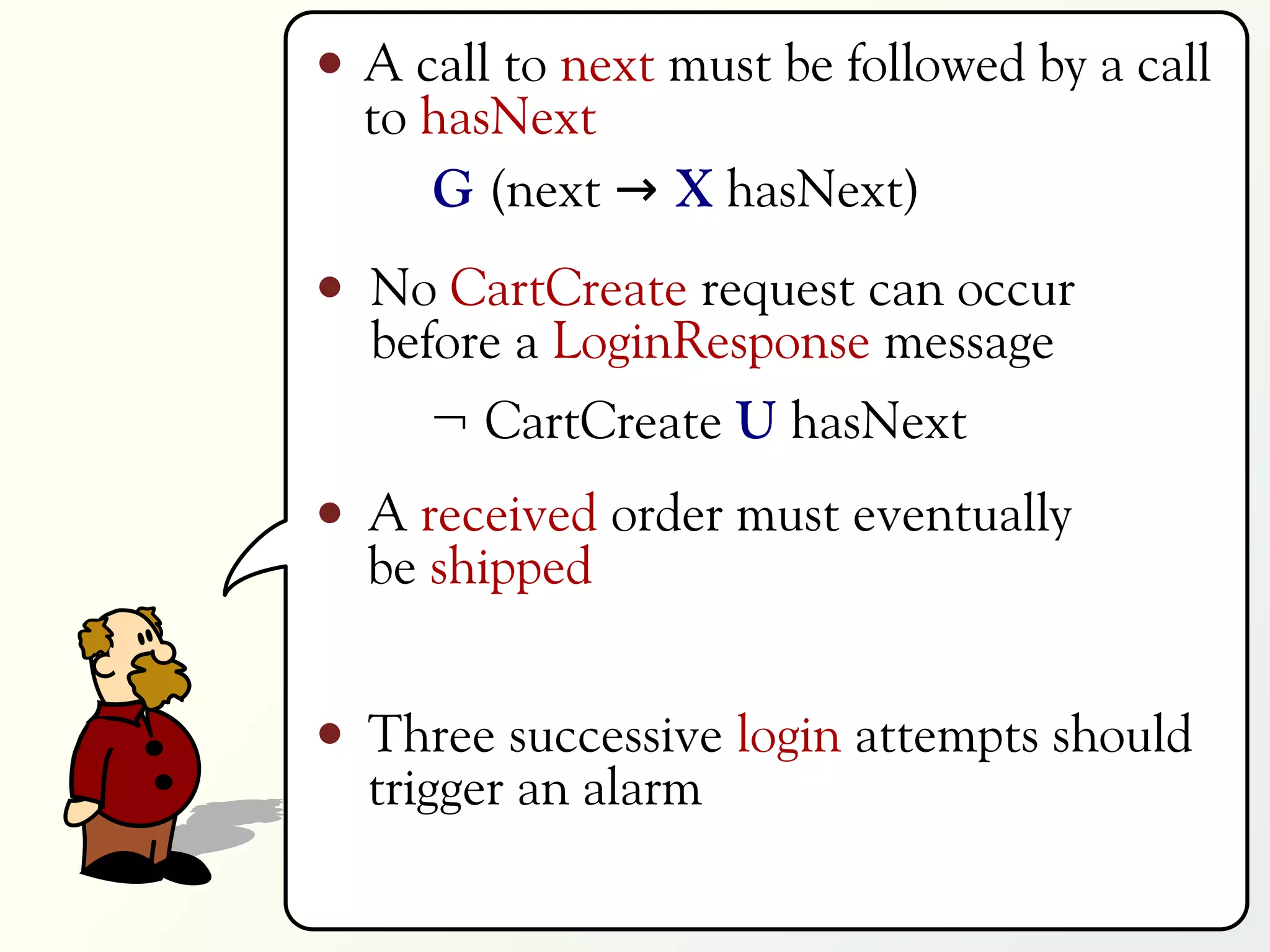
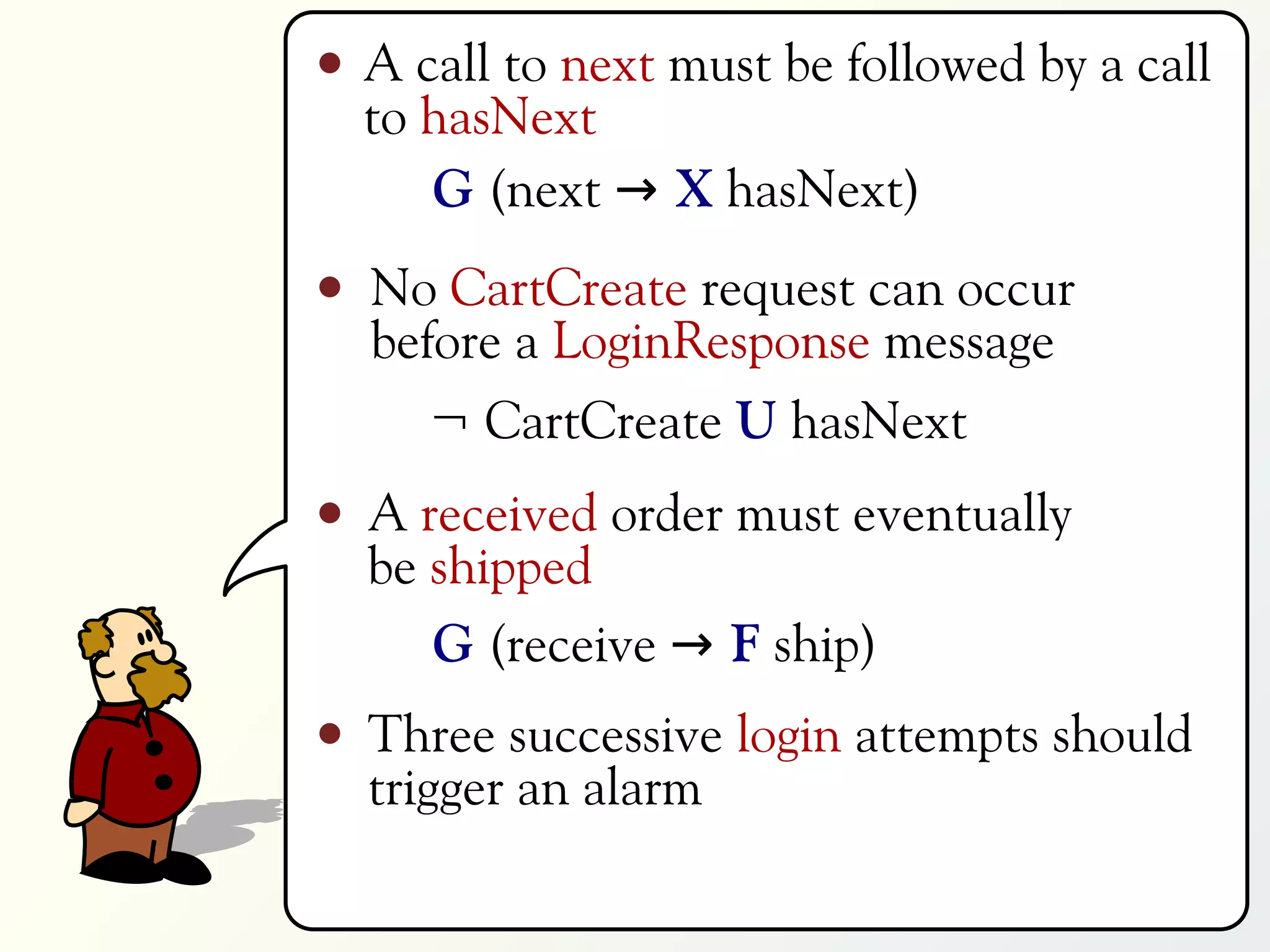
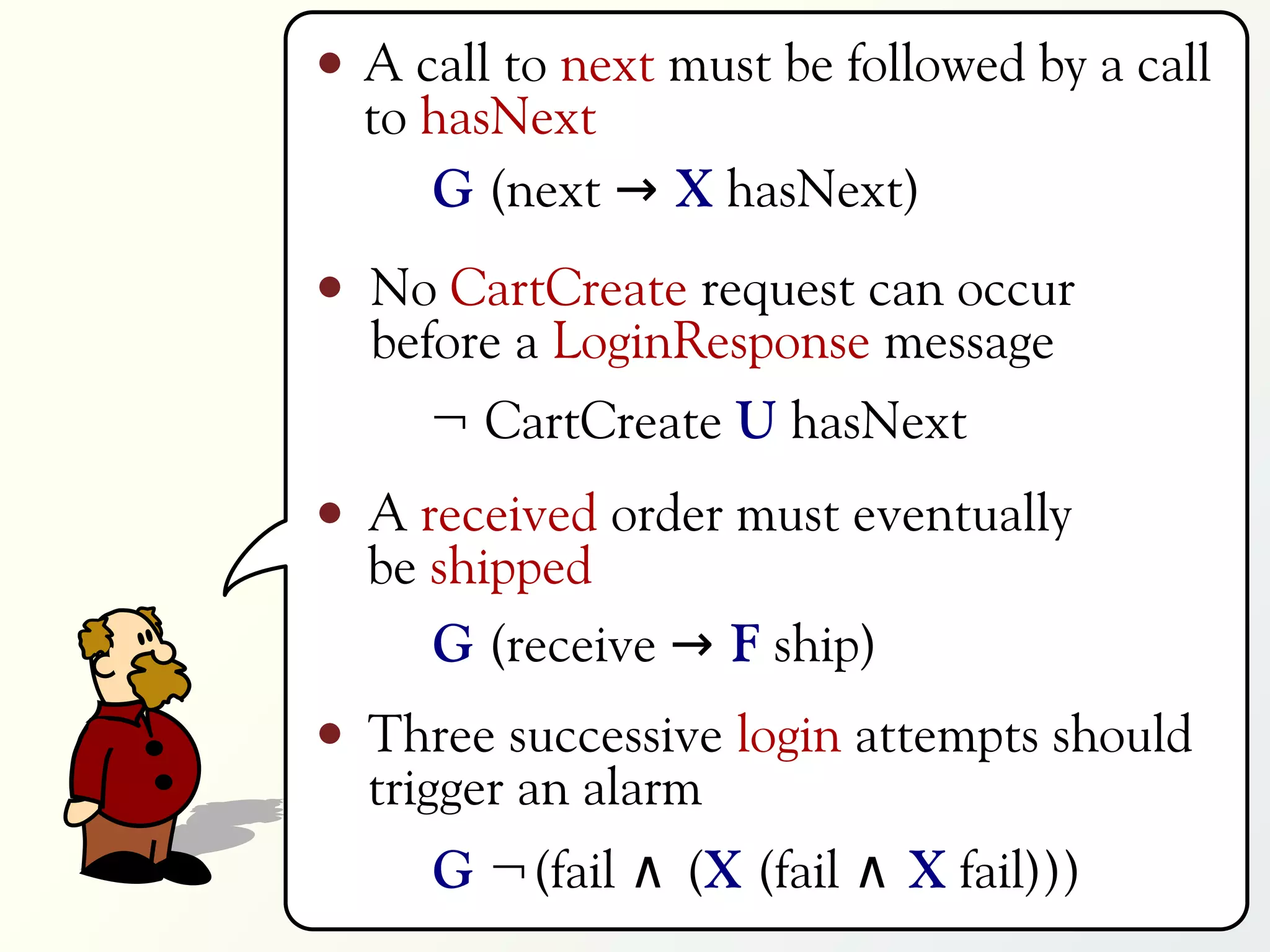
1 G p₀ ≠ 0
2 G (p₀ = 0 → X p₁ = 0)
3 ∀x ∈ [0,9] : G (p₀ = x → X p₁ = x)
4 ∃m ∈ [0,9] : ∀x ∈ [0,9] :
G (p m = x → X X p m ≠ x)

119. Property 1 2 3 4
Tuples 55 k 120 k 600 k 5 M
Time/event 19 μs 23 μs 75 μs 985 μs
Sequential ratio 100% 92% 92% 3%
Inferred time 19 μs 21 μs 14 μs 30 μs

120. Questions?
M