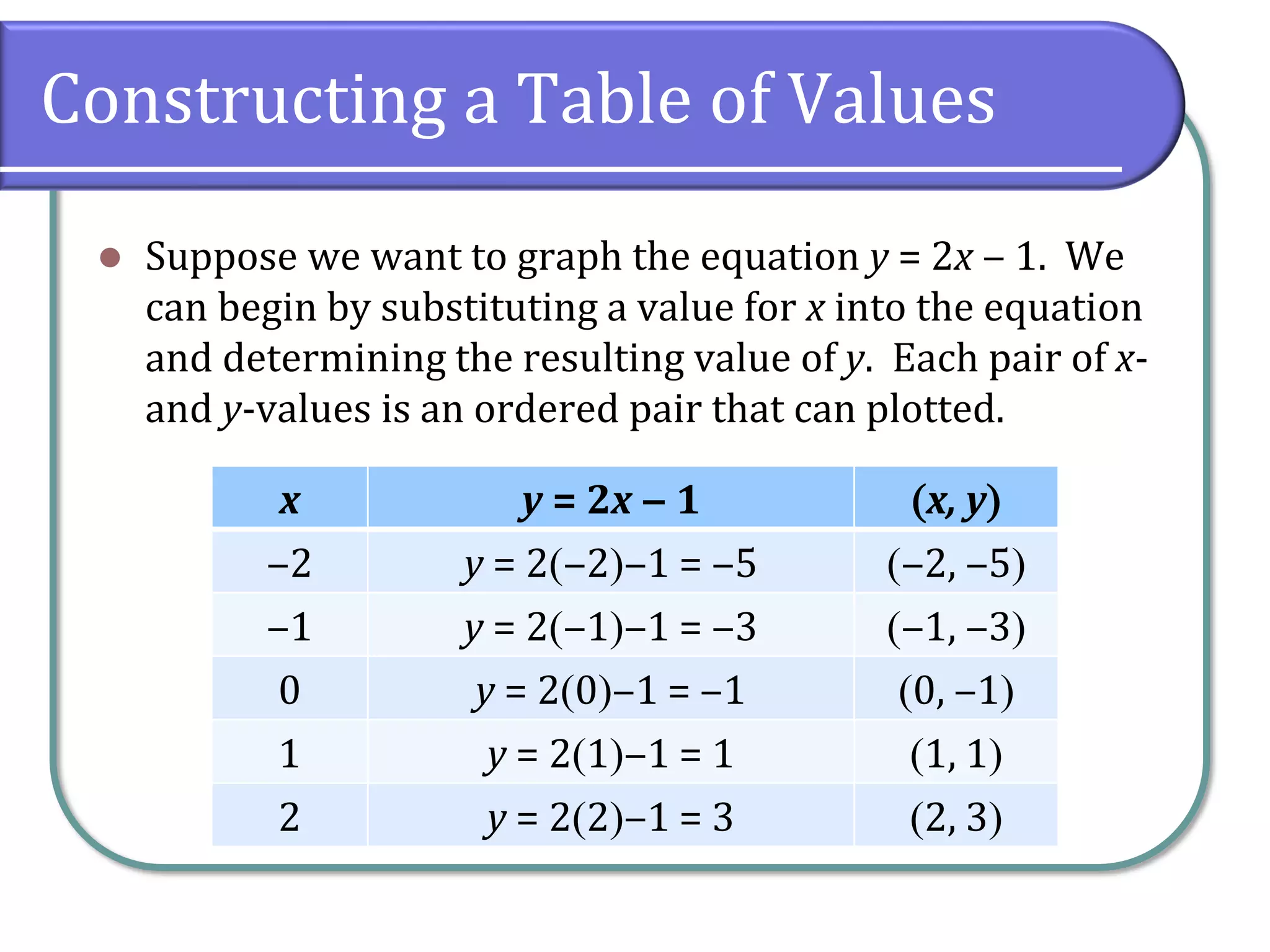
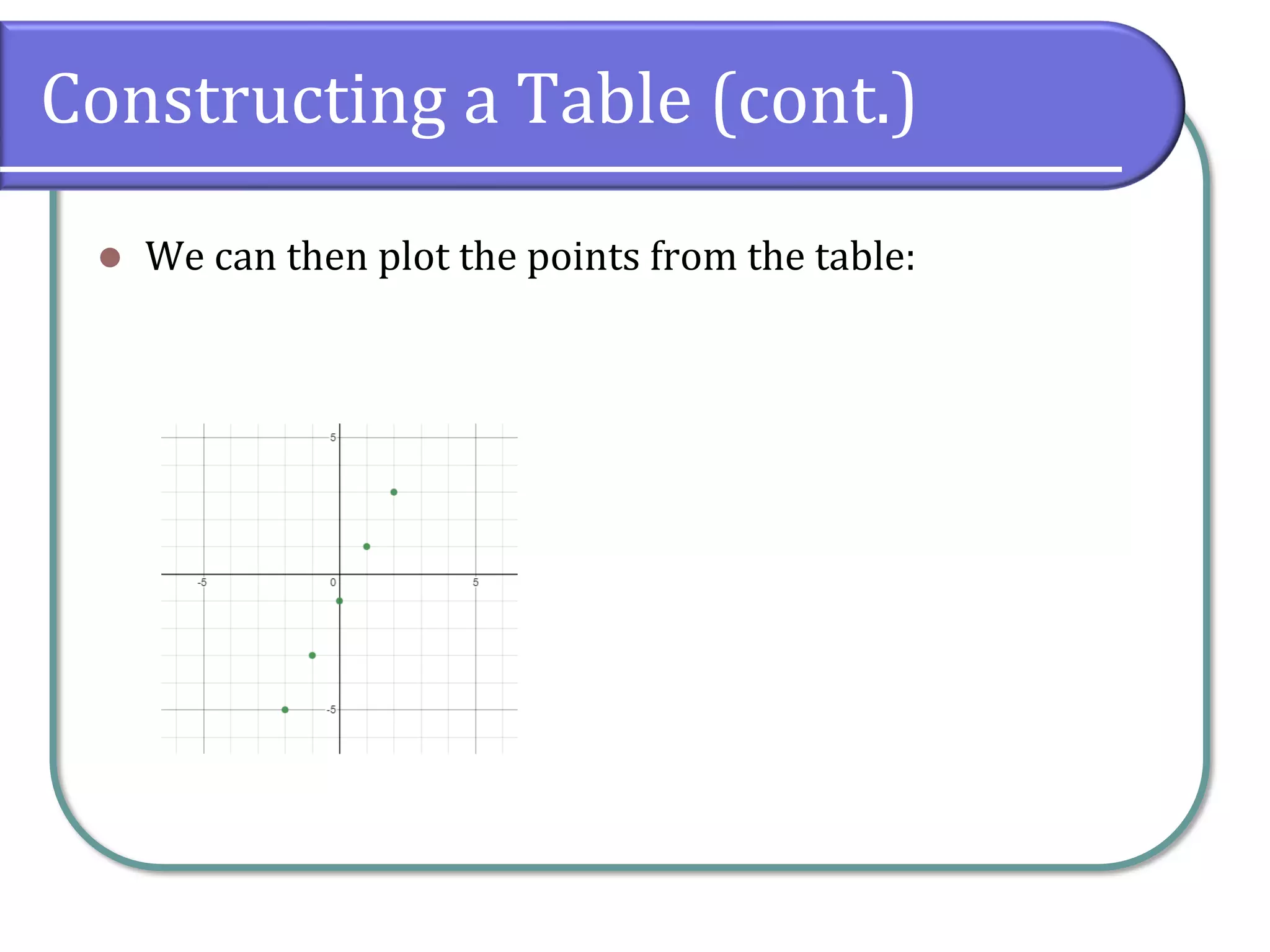
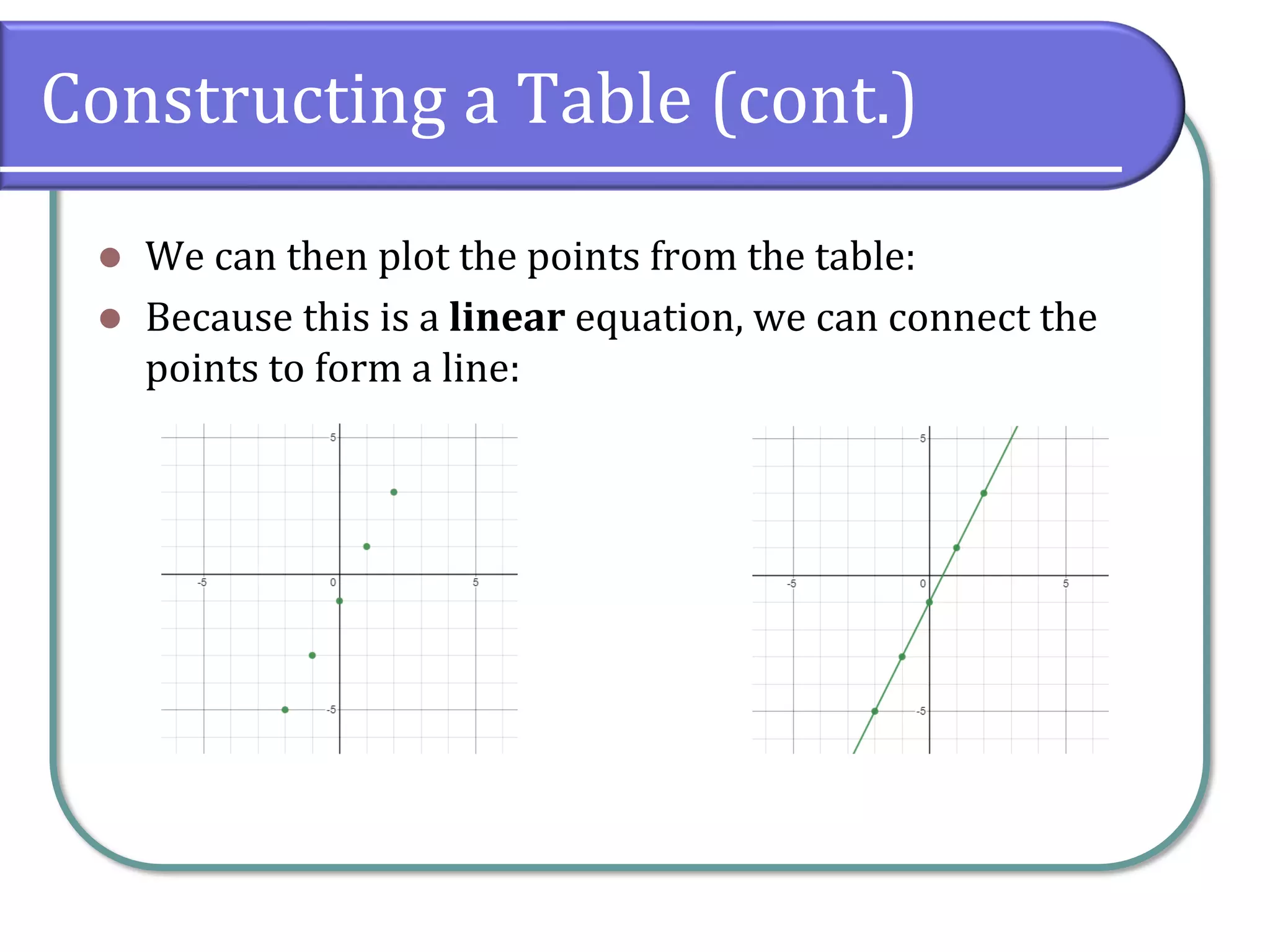
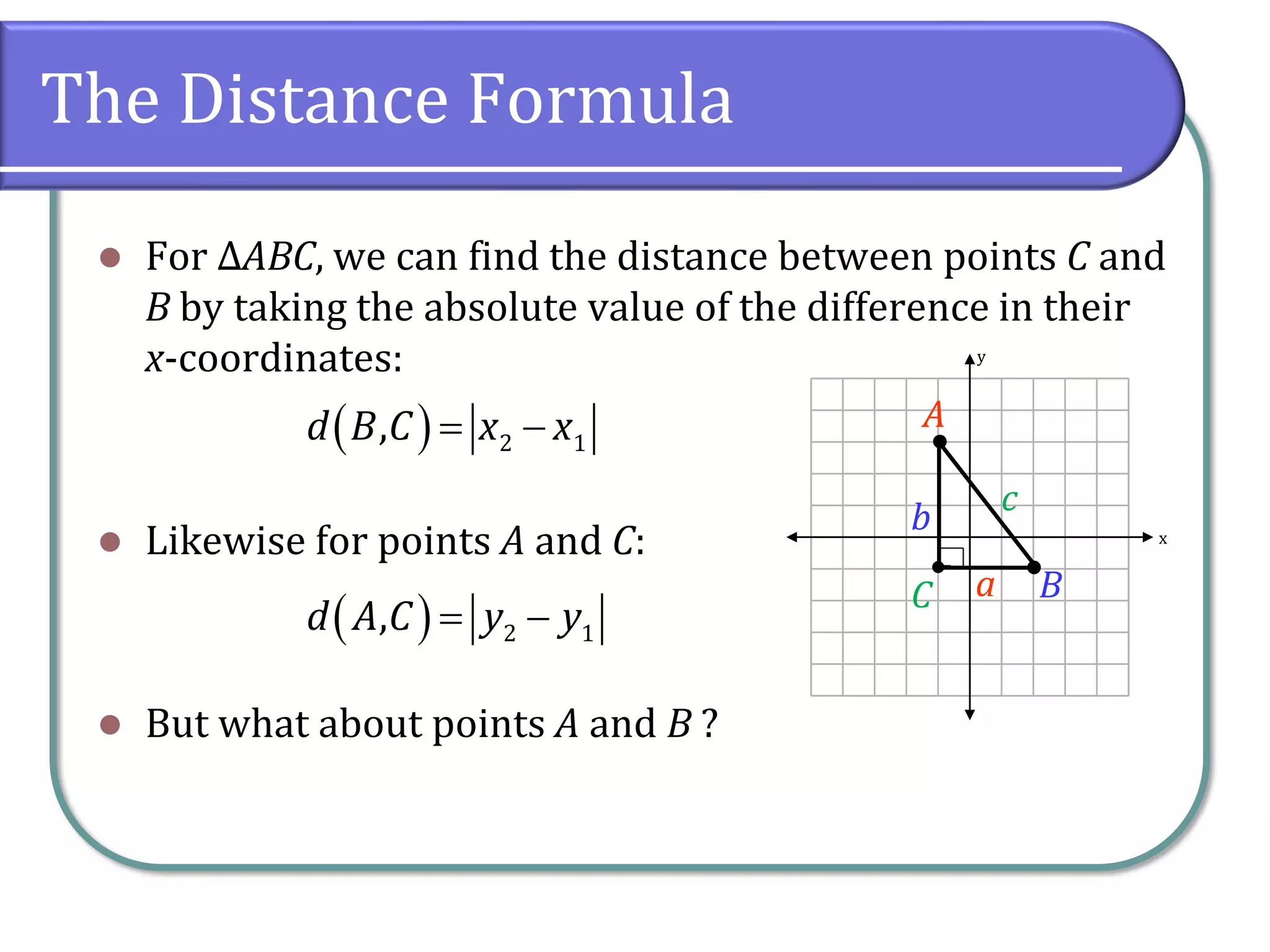
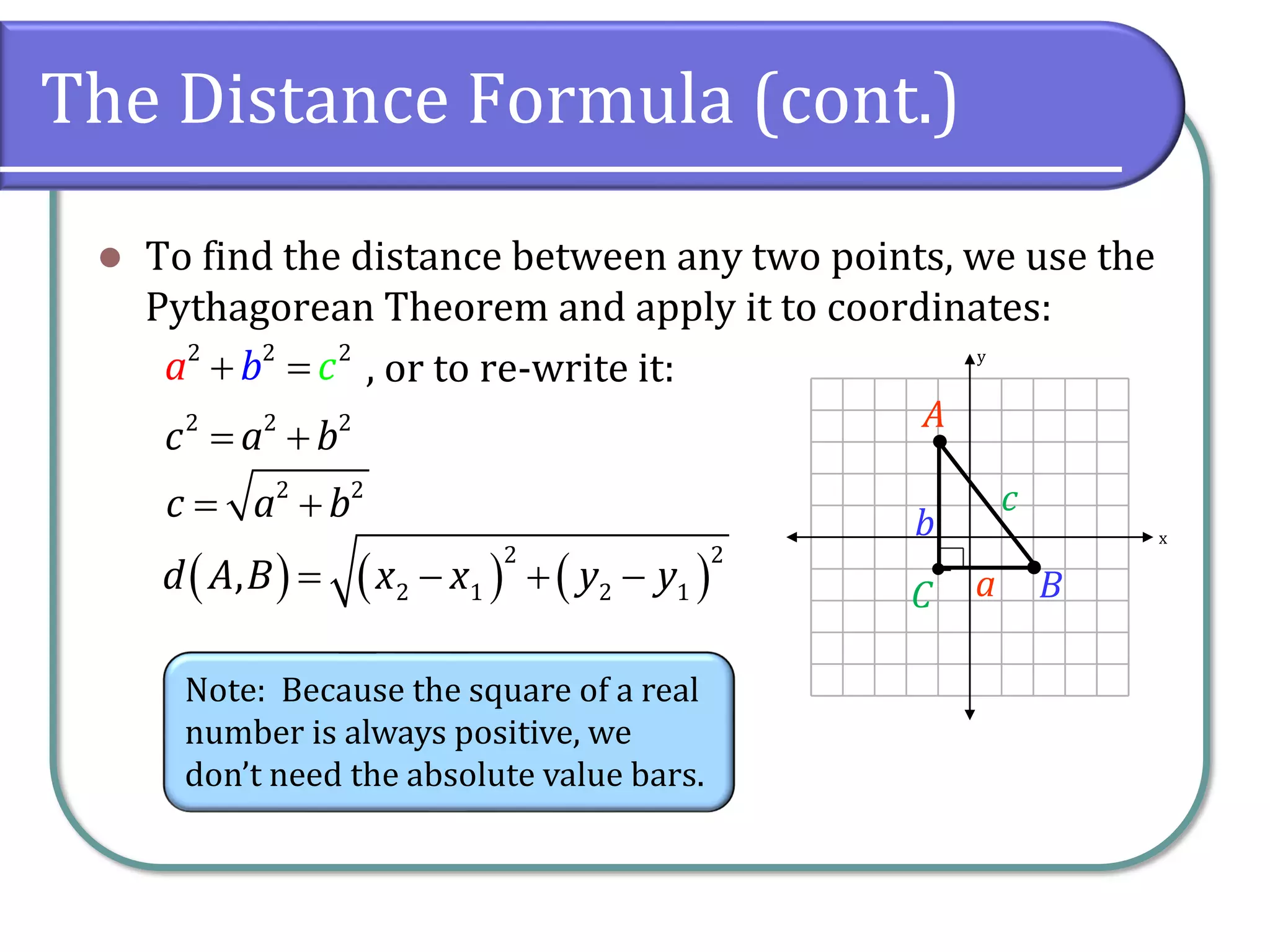
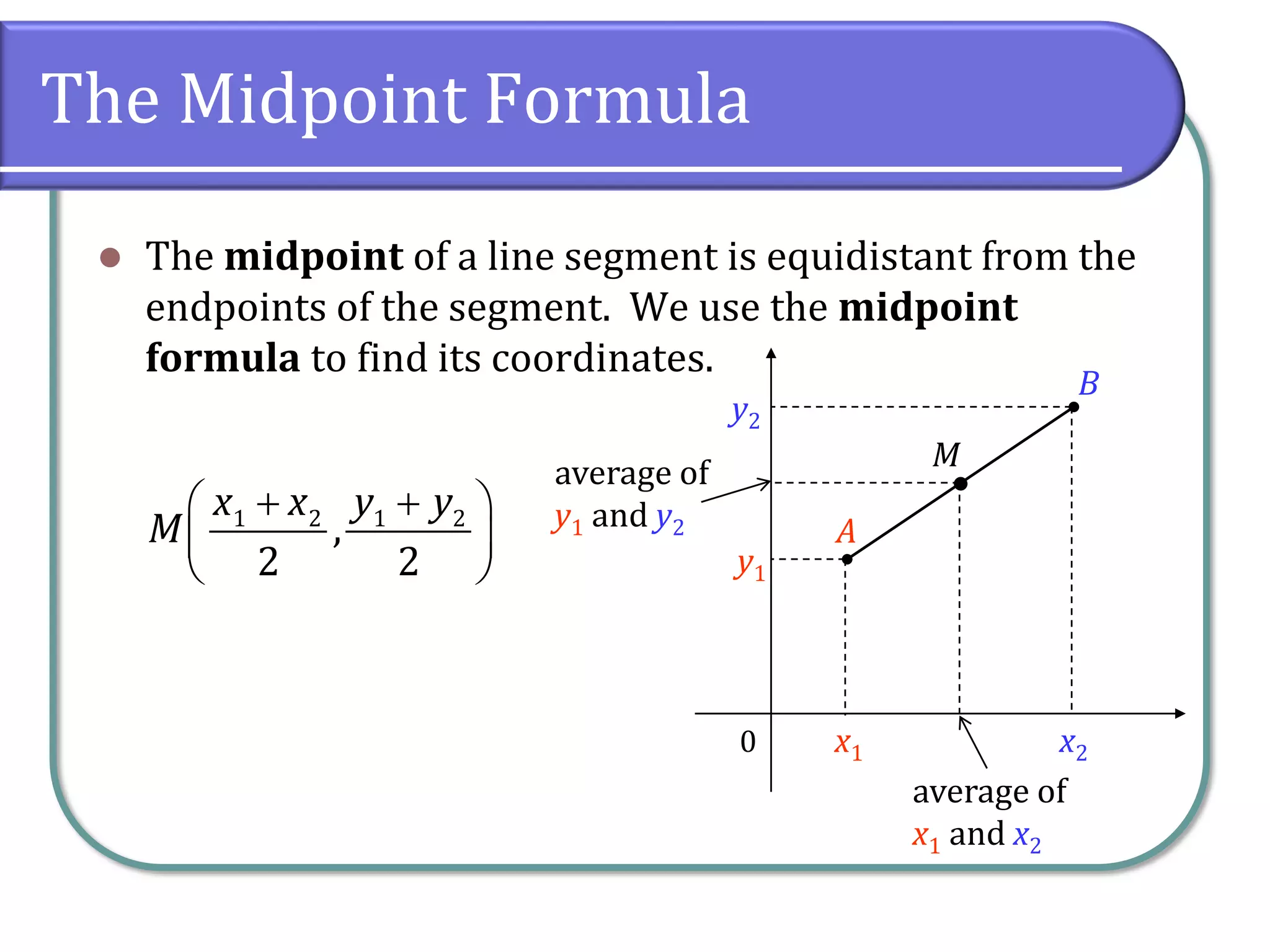
This section covers rectangular coordinates, including how to plot ordered pairs, graph equations, and find intercepts. It introduces the distance and midpoint formulas for calculating distances and midpoints between points on a Cartesian coordinate system. Additionally, examples are provided to illustrate the application of these concepts, such as constructing tables of values and using formulas to find specific points.