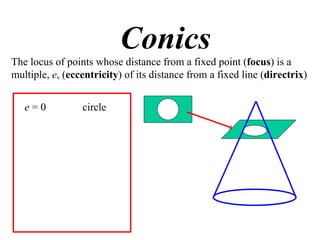
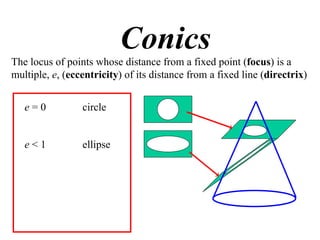
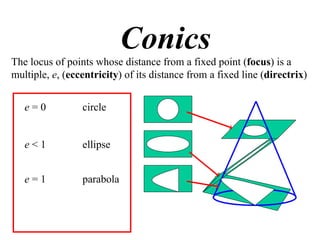
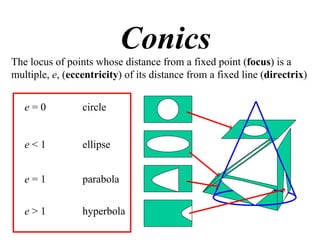
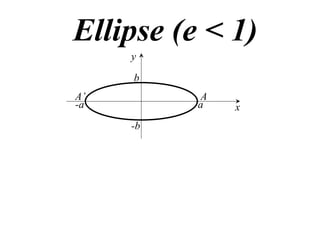
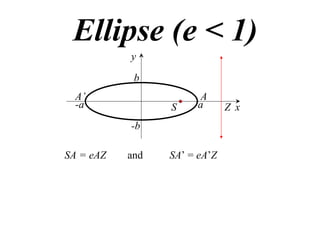
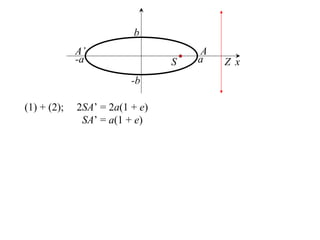
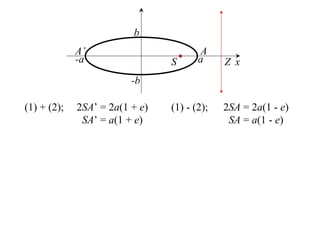
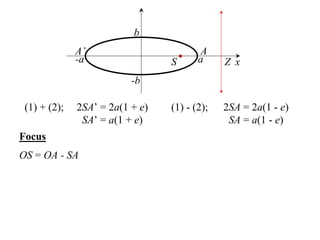
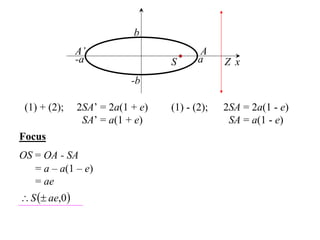
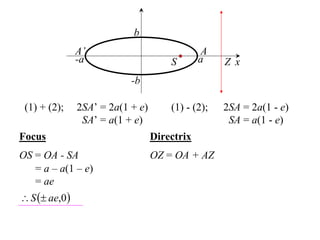
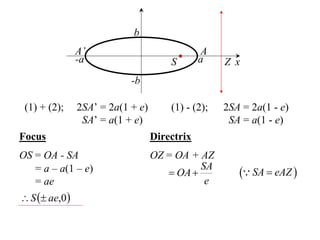
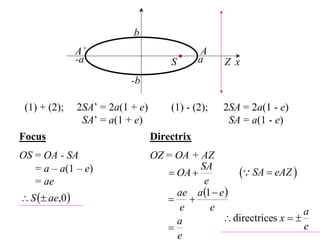
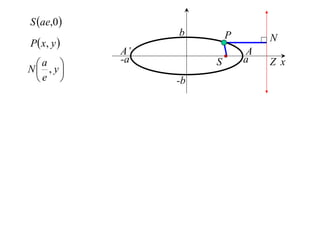
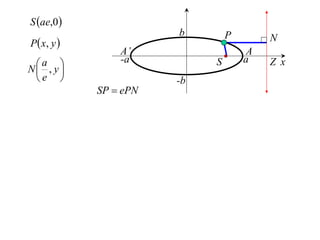
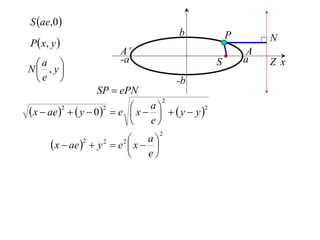
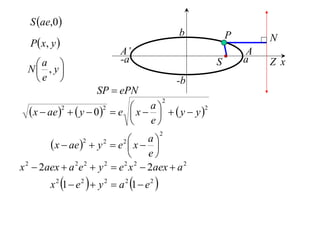
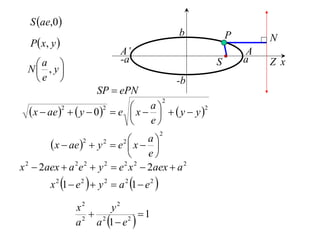
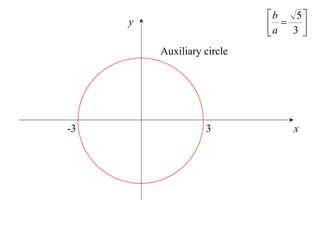
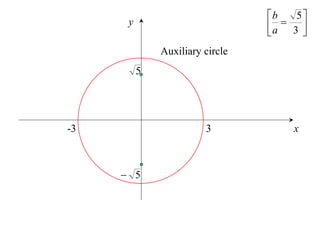
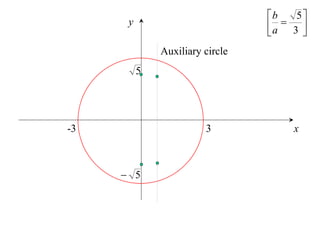
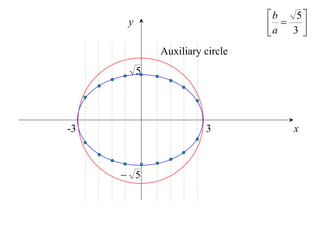
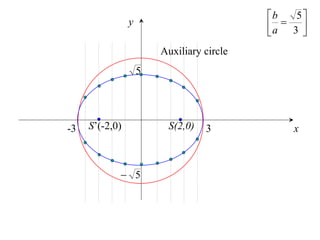
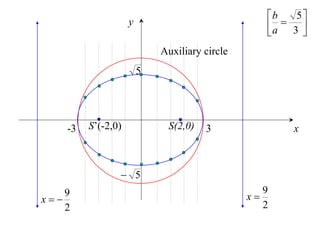
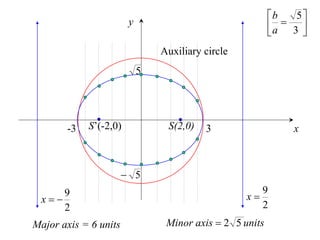
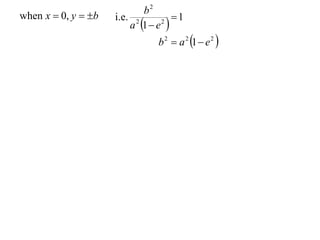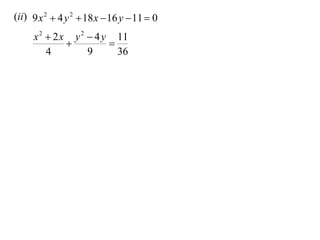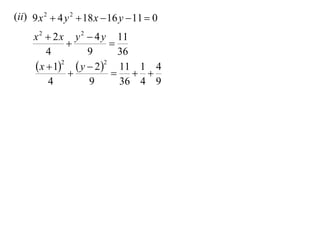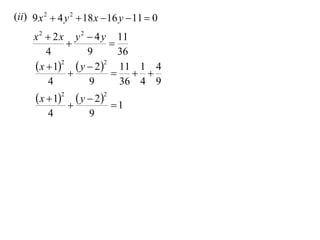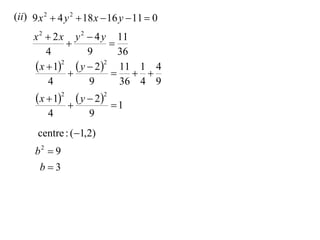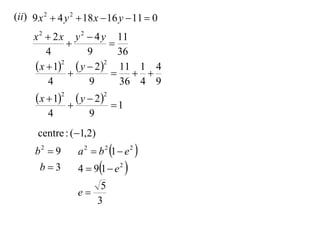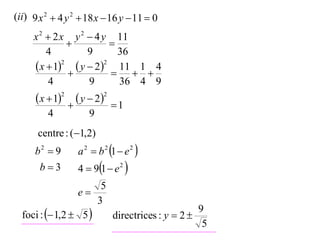The document discusses conic sections, specifically the ellipse. An ellipse is defined as the locus of points where the sum of the distances from two fixed points (foci) is a constant. For an ellipse, the eccentricity e is less than 1. The foci of an ellipse lie on the major axis, and the distance from each focus to any point on the ellipse follows the relationship d=ae, where a is the semimajor axis. The semiminor axis b is given by b2=a2(1-e2).

1. Conics

2. Conics
The locus of points whose distance from a fixed point (focus) is a
multiple, e, (eccentricity) of its distance from a fixed line (directrix)

3. Conics
The locus of points whose distance from a fixed point (focus) is a
multiple, e, (eccentricity) of its distance from a fixed line (directrix)

4. Conics
The locus of points whose distance from a fixed point (focus) is a
multiple, e, (eccentricity) of its distance from a fixed line (directrix)
e=0 circle

5. Conics
The locus of points whose distance from a fixed point (focus) is a
multiple, e, (eccentricity) of its distance from a fixed line (directrix)
e=0 circle
e<1 ellipse

6. Conics
The locus of points whose distance from a fixed point (focus) is a
multiple, e, (eccentricity) of its distance from a fixed line (directrix)
e=0 circle
e<1 ellipse
e=1 parabola

7. Conics
The locus of points whose distance from a fixed point (focus) is a
multiple, e, (eccentricity) of its distance from a fixed line (directrix)
e=0 circle
e<1 ellipse
e=1 parabola
e>1 hyperbola

8. Ellipse (e < 1)
y
b
A’ A
-a a x
-b

9. Ellipse (e < 1)
y
b
A’ A
-a S a Z x
-b

10. Ellipse (e < 1)
y
b
A’ A
-a S a Z x
-b
SA = eAZ and SA’ = eA’Z

11. Ellipse (e < 1)
y
b
A’ A
-a S a Z x
-b
SA = eAZ and SA’ = eA’Z
(1) SA’ + SA = 2a
(2) SA’ – SA = e(A’Z – AZ)

12. Ellipse (e < 1)
y
b
A’ A
-a S a Z x
-b
SA = eAZ and SA’ = eA’Z
(1) SA’ + SA = 2a
(2) SA’ – SA = e(A’Z – AZ)
= e(AA’)
= e(2a)
= 2ae

13. b
A’ A
-a S a Z x
-b
(1) + (2); 2SA’ = 2a(1 + e)
SA’ = a(1 + e)

14. b
A’ A
-a S a Z x
-b
(1) + (2); 2SA’ = 2a(1 + e) (1) - (2); 2SA = 2a(1 - e)
SA’ = a(1 + e) SA = a(1 - e)

15. b
A’ A
-a S a Z x
-b
(1) + (2); 2SA’ = 2a(1 + e) (1) - (2); 2SA = 2a(1 - e)
SA’ = a(1 + e) SA = a(1 - e)
Focus
OS = OA - SA

16. b
A’ A
-a S a Z x
-b
(1) + (2); 2SA’ = 2a(1 + e) (1) - (2); 2SA = 2a(1 - e)
SA’ = a(1 + e) SA = a(1 - e)
Focus
OS = OA - SA
= a – a(1 – e)
= ae
 S  ae,0 

17. b
A’ A
-a S a Z x
-b
(1) + (2); 2SA’ = 2a(1 + e) (1) - (2); 2SA = 2a(1 - e)
SA’ = a(1 + e) SA = a(1 - e)
Focus Directrix
OS = OA - SA OZ = OA + AZ
= a – a(1 – e)
= ae
 S  ae,0 

18. b
A’ A
-a S a Z x
-b
(1) + (2); 2SA’ = 2a(1 + e) (1) - (2); 2SA = 2a(1 - e)
SA’ = a(1 + e) SA = a(1 - e)
Focus Directrix
OS = OA - SA OZ = OA + AZ
SA
= a – a(1 – e)  OA   SA  eAZ 
= ae e
 S  ae,0 

19. b
A’ A
-a S a Z x
-b
(1) + (2); 2SA’ = 2a(1 + e) (1) - (2); 2SA = 2a(1 - e)
SA’ = a(1 + e) SA = a(1 - e)
Focus Directrix
OS = OA - SA OZ = OA + AZ
SA
= a – a(1 – e)  OA   SA  eAZ 
= ae e
ae a1  e 
 S  ae,0   
e e a
a  directrices x  
 e
e

20. S ae,0 
b P
P  x, y 
N
A’ A
-a a
N , y
a S Z x
 
e  -b

21. S ae,0 
b P
P  x, y 
N
A’ A
-a a
N , y
a S Z x
 
e  -b
SP  ePN

22. S ae,0 
b P
P  x, y 
N
A’ A
-a a
N , y
a S Z x
 
e  -b
SP  ePN
2
 x  ae 2   y  02  e  x     y  y 2
a
 
 e
2
2 a
 x  ae   y  e  x  
2 2
 e

23. S ae,0 
b P
P  x, y 
N
A’ A
-a a
N , y
a S Z x
 
e  -b
SP  ePN
2
 x  ae 2   y  02  e  x     y  y 2
a
 
 e
2
2 a
 x  ae   y  e  x  
2 2
 e
x 2  2aex  a 2 e 2  y 2  e 2 x 2  2aex  a 2
x 2 1  e 2   y 2  a 2 1  e 2 

24. S ae,0 
b P
P  x, y 
N
A’ A
-a a
N , y
a S Z x
 
e  -b
SP  ePN
2
 x  ae 2   y  02  e  x     y  y 2
a
 
 e
2
2 a
 x  ae   y  e  x  
2 2
 e
x 2  2aex  a 2 e 2  y 2  e 2 x 2  2aex  a 2
x 2 1  e 2   y 2  a 2 1  e 2 
x2 y2
 2 1
a a 1  e 
2 2

25. b2
when x  0, y  b 1
a 1  e 
i.e. 2 2
b 2  a 2 1  e 2 

26. b2
when x  0, y  b 1
a 1  e 
i.e. 2 2
b 2  a 2 1  e 2 
Ellipse: (a > b) x2 y2
2
 2 1
a b
where; b 2  a 2 1  e 2 
focus :  ae,0 
a
directrices : x  
e
e is the eccentricity
major semi-axis = a units
minor semi-axis = b units

27. b2
when x  0, y  b 1
a 1  e 
i.e. 2 2
b 2  a 2 1  e 2 
Ellipse: (a > b) x2 y2 Note: If b > a
2
 2 1
a b foci on the y axis
where; b  a 1  e
2 2 2
 a 2  b 2 1  e 2 
focus :  ae,0  focus : 0,be 
a b
directrices : x   directrices : y  
e e
e is the eccentricity
major semi-axis = a units
minor semi-axis = b units

28. b2
when x  0, y  b 1
a 1  e 
i.e. 2 2
b 2  a 2 1  e 2 
Ellipse: (a > b) x2 y2 Note: If b > a
2
 2 1
a b foci on the y axis
where; b  a 1  e
2 2 2
 a 2  b 2 1  e 2 
focus :  ae,0  focus : 0,be 
a b
directrices : x   directrices : y  
e e
e is the eccentricity
major semi-axis = a units Area  ab
minor semi-axis = b units

29. e.g. Find the eccentricity, foci and directrices of the ellipse
x2 y2
  1 and sketch the ellipse showing all of the important
9 5
features.

30. e.g. Find the eccentricity, foci and directrices of the ellipse
x2 y2
  1 and sketch the ellipse showing all of the important
9 5
features.
x2 y2
 1
9 5
a2  9
a3

31. e.g. Find the eccentricity, foci and directrices of the ellipse
x2 y2
  1 and sketch the ellipse showing all of the important
9 5
features.
x2 y2
 1 b2  5
9 5
a 2 1  e 2   5
a2  9
a3

32. e.g. Find the eccentricity, foci and directrices of the ellipse
x2 y2
  1 and sketch the ellipse showing all of the important
9 5
features.
x2 y2
 1 b2  5
9 5
a 2 1  e 2   5
91  e 2   5
a2  9
a3
5
1 e 2
9
4
e 
2
9
2
e
3

33. e.g. Find the eccentricity, foci and directrices of the ellipse
x2 y2
  1 and sketch the ellipse showing all of the important
9 5
features.
x2 y2
 1 b2  5
9 5
a 2 1  e 2   5
91  e 2   5
a2  9
2
a3  eccentricity 
5 3
1 e 2
9 foci :  2,0 
4
e 
2
3
9 directrices : x  3 
2
2
e 9
3 x
2

34. y
Auxiliary circle
-3 3 x

35. b 5
y a  3 
 
Auxiliary circle
-3 3 x

36. b 5
y a  3 
 
Auxiliary circle
5
-3 3 x
 5

37. b 5
y a  3 
 
Auxiliary circle
5
-3 3 x
 5

38. b 5
y a  3 
 
Auxiliary circle
5
-3 3 x
 5

39. b 5
y a  3 
 
Auxiliary circle
5
-3 3 x
 5

40. b 5
y a  3 
 
Auxiliary circle
5
-3 3 x
 5

41. b 5
y a  3 
 
Auxiliary circle
5
-3 3 x
 5

42. b 5
y a  3 
 
Auxiliary circle
5
-3 3 x
 5

43. b 5
y a  3 
 
Auxiliary circle
5
-3 S’(-2,0) S(2,0) 3 x
 5

44. b 5
y a  3 
 
Auxiliary circle
5
-3 S’(-2,0) S(2,0) 3 x
 5
9 9
x x
2 2

45. b 5
y a  3 
 
Auxiliary circle
5
-3 S’(-2,0) S(2,0) 3 x
 5
9 9
x x
2 2
Major axis = 6 units Minor axis  2 5 units

46. (ii) 9 x 2  4 y 2  18 x  16 y  11  0

47. (ii) 9 x 2  4 y 2  18 x  16 y  11  0
x 2  2 x y 2  4 y 11
 
4 9 36

48. (ii) 9 x 2  4 y 2  18 x  16 y  11  0
x 2  2 x y 2  4 y 11
 
4 9 36
 x  12  y  22 11 1 4
   
4 9 36 4 9

49. (ii) 9 x 2  4 y 2  18 x  16 y  11  0
x 2  2 x y 2  4 y 11
 
4 9 36
 x  12  y  22 11 1 4
   
4 9 36 4 9
 x  12  y  22
 1
4 9

50. (ii) 9 x 2  4 y 2  18 x  16 y  11  0
x 2  2 x y 2  4 y 11
 
4 9 36
 x  12  y  22 11 1 4
   
4 9 36 4 9
 x  12  y  22
 1
4 9
centre : (1,2)

51. (ii) 9 x 2  4 y 2  18 x  16 y  11  0
x 2  2 x y 2  4 y 11
 
4 9 36
 x  12  y  22 11 1 4
   
4 9 36 4 9
 x  12  y  22
 1
4 9
centre : (1,2)
b2  9
b3

52. (ii) 9 x 2  4 y 2  18 x  16 y  11  0
x 2  2 x y 2  4 y 11
 
4 9 36
 x  12  y  22 11 1 4
   
4 9 36 4 9
 x  12  y  22
 1
4 9
centre : (1,2)
b2  9 a 2  b 2 1  e 2 
b3 4  91  e 2 
5
e
3

53. (ii) 9 x 2  4 y 2  18 x  16 y  11  0
x 2  2 x y 2  4 y 11
 
4 9 36
 x  12  y  22 11 1 4
   
4 9 36 4 9
 x  12  y  22
 1
4 9
centre : (1,2)
b2  9 a 2  b 2 1  e 2 
b3 4  91  e 2 
5
e
3
foci :  1,2  5 
9
directrices : y  2 
5

54. (ii) 9 x 2  4 y 2  18 x  16 y  11  0
x 2  2 x y 2  4 y 11
 
4 9 36
 x  12  y  22 11 1 4
   
4 9 36 4 9
 x  12  y  22 Exercise 6A; 1, 2, 3, 5, 7,
 1
4 9 8, 9, 11, 13, 15
centre : (1,2)
b2  9 a 2  b 2 1  e 2 
b3 4  91  e 2 
5
e
3
foci :  1,2  5 
9
directrices : y  2 
5