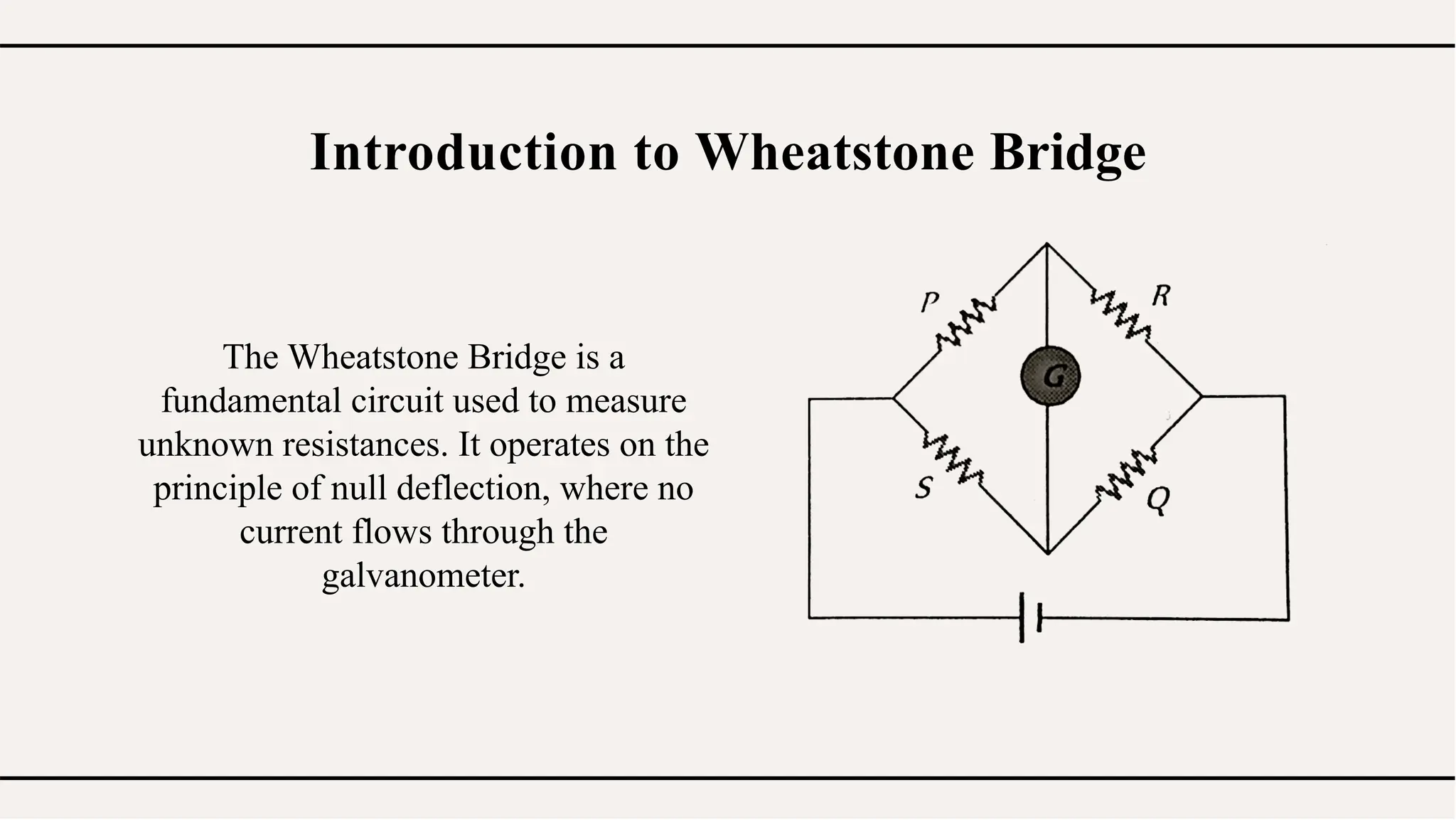
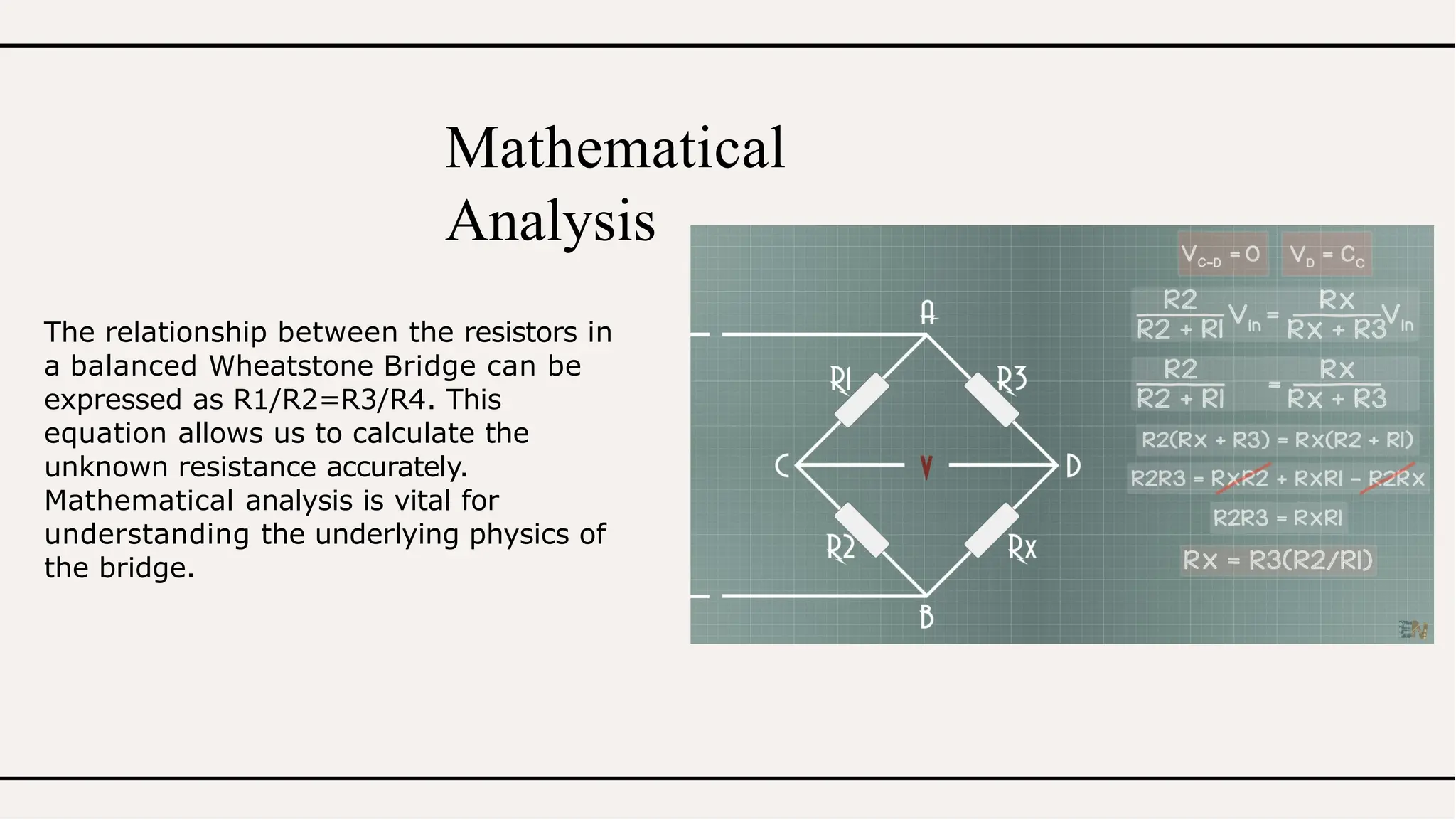
The Wheatstone bridge is a critical circuit for measuring unknown resistances based on the principle of null deflection. It operates by balancing resistors to achieve zero current across a galvanometer, allowing for precise resistance measurement while having limitations in unstable conditions and for extreme resistance values. Its applications span various fields, including strain gauges and temperature sensors, making it an essential concept in electrical engineering.

1. Wheatstone Bridge
Principles and Applications

2. Introduction to Wheatstone Bridge
The Wheatstone Bridge is a
fundamental circuit used to measure
unknown resistances. It operates on the
principle of null deflection, where no
current flows through the
galvanometer.

3. The Wheatstone Bridge functions based
on the balance of resistance. By
adjusting known resistances, the bridge
reaches a state where the potential
difference across the galvanometer is
zero. This principle allows for precise
measurement of an unknown resistance.
Basic Principles

4. The relationship between the resistors in
a balanced Wheatstone Bridge can be
expressed as R1/R2=R3/R4. This
equation allows us to calculate the
unknown resistance accurately.
Mathematical analysis is vital for
understanding the underlying physics of
the bridge.
Mathematical
Analysis

5. Despite its advantages, the Wheatstone Bridge has
some limitations.
It requires a stable power supply and is less effective
for very low or very high resistances.
Understanding these limitations helps in selecting the
right method for measurement of resistance.
Limitations of the Wheatstone Bridge

6. In real-world applications, the Wheatstone
Bridge is used in strain gauges,
temperature sensors, and more. These
examples demonstrate its versatility and
importance in engineering and
technology. Understanding these
applications bridges theory and practical
use.
Real-World Examples

7. In conclusion, the Wheatstone Bridge is
a
crucial tool in physics for measuring
resistances accurately. Its principles,
components, and applications provide a
strong foundation for students. Mastering
this concept is essential for further
studies in electrical engineering and
related fields.
Conclusion
Charles Wheatstone