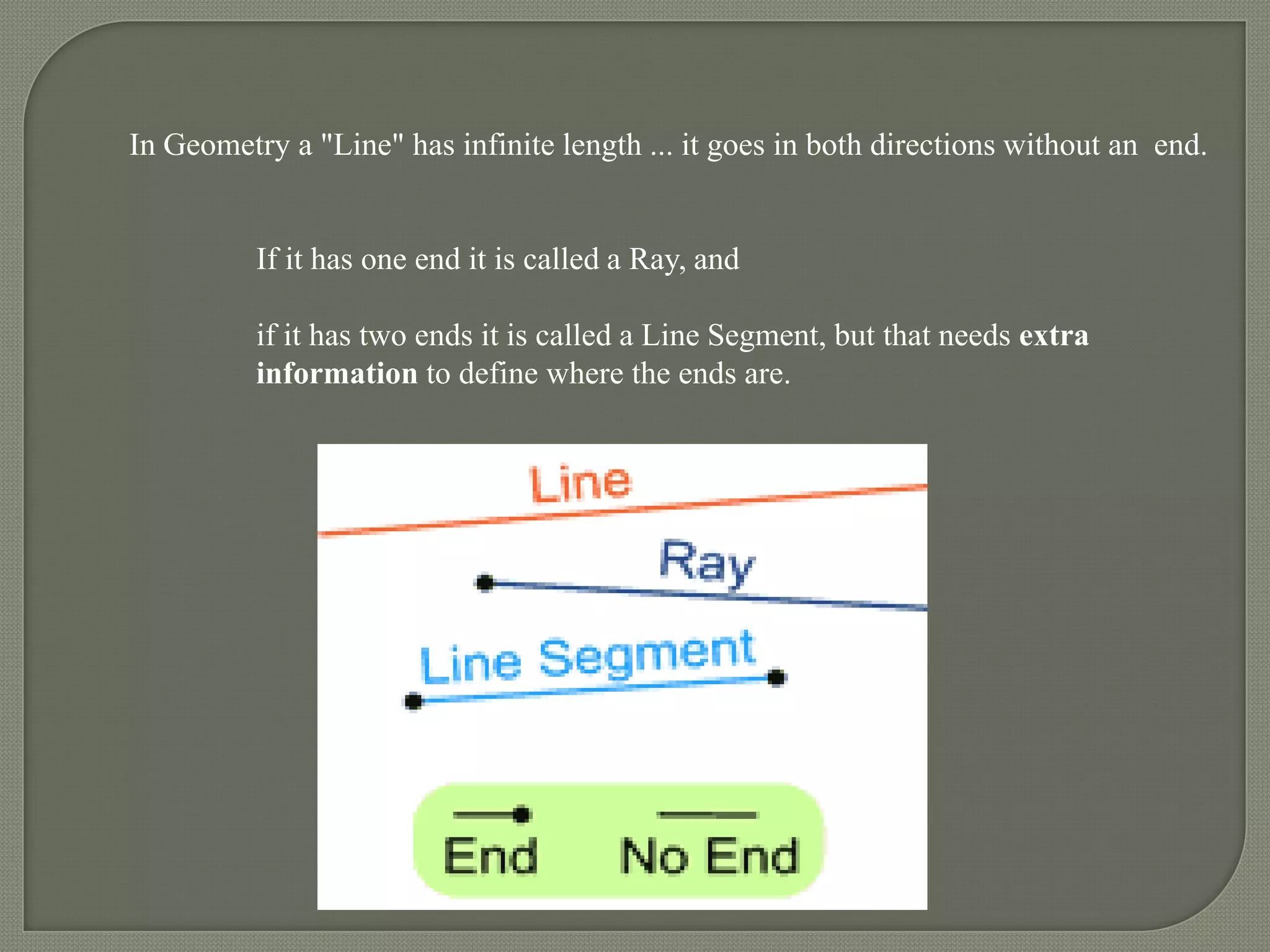
Infinity is an endless, boundless idea that cannot be measured and does not behave like a real number. Some key properties of infinity include that any real number added to or multiplied by infinity is infinity, and infinity plus or multiplied by itself is also infinity. While infinity can be used like a number in some cases, some operations involving infinity like dividing infinity by infinity are undefined.

1. What is Infinity?
Infinity ...?
... it's big ...
... it's huge ...
... it's tremendously large ...
... it's extremely humongosly enormous ...
... it's ... Endless!

2. Infinity is an idea that has no end
In our world, we don't have anything like it.
So Just think infinity as an idea that is
"endless", or "boundless".
Infinity is not a real number
It is an idea
An idea of something without an end.
Infinity cannot be measured.

3. In Geometry a "Line" has infinite length ... it goes in both directions without an end.
If it has one end it is called a Ray, and
if it has two ends it is called a Line Segment, but that needs extra
information to define where the ends are.

4. We can sometimes use infinity like it is a number, but also infinity
does not behave like a real number.
For example: ∞ + 1 = ∞
Which says that infinity plus one is still equal to infinity.
If something is already endless,
you can add 1 and it will still be endless.
The most important thing about infinity is that:
∞ <x< ∞
Which is mathematical shorthand for
"minus infinity is less than any real number,
and infinity is greater than any real number"

5. Special Properties of Infinity
∞+∞=∞
-∞ + -∞ = -∞
∞×∞=∞
-∞ × -∞ = ∞
-∞ × ∞ = -∞
Some properties x+∞=∞
x + (-∞) = -∞
x - ∞ = -∞
x - (-∞) = ∞
For x>0 :
x×∞=∞
x × (-∞) = -∞
For x<0 :
x × ∞ = -∞
x × (-∞) = ∞

6. "Undefined" Operations
0×∞
0 × -∞
∞ + -∞
Some undefined properties
∞-∞
∞/∞
∞0
1∞