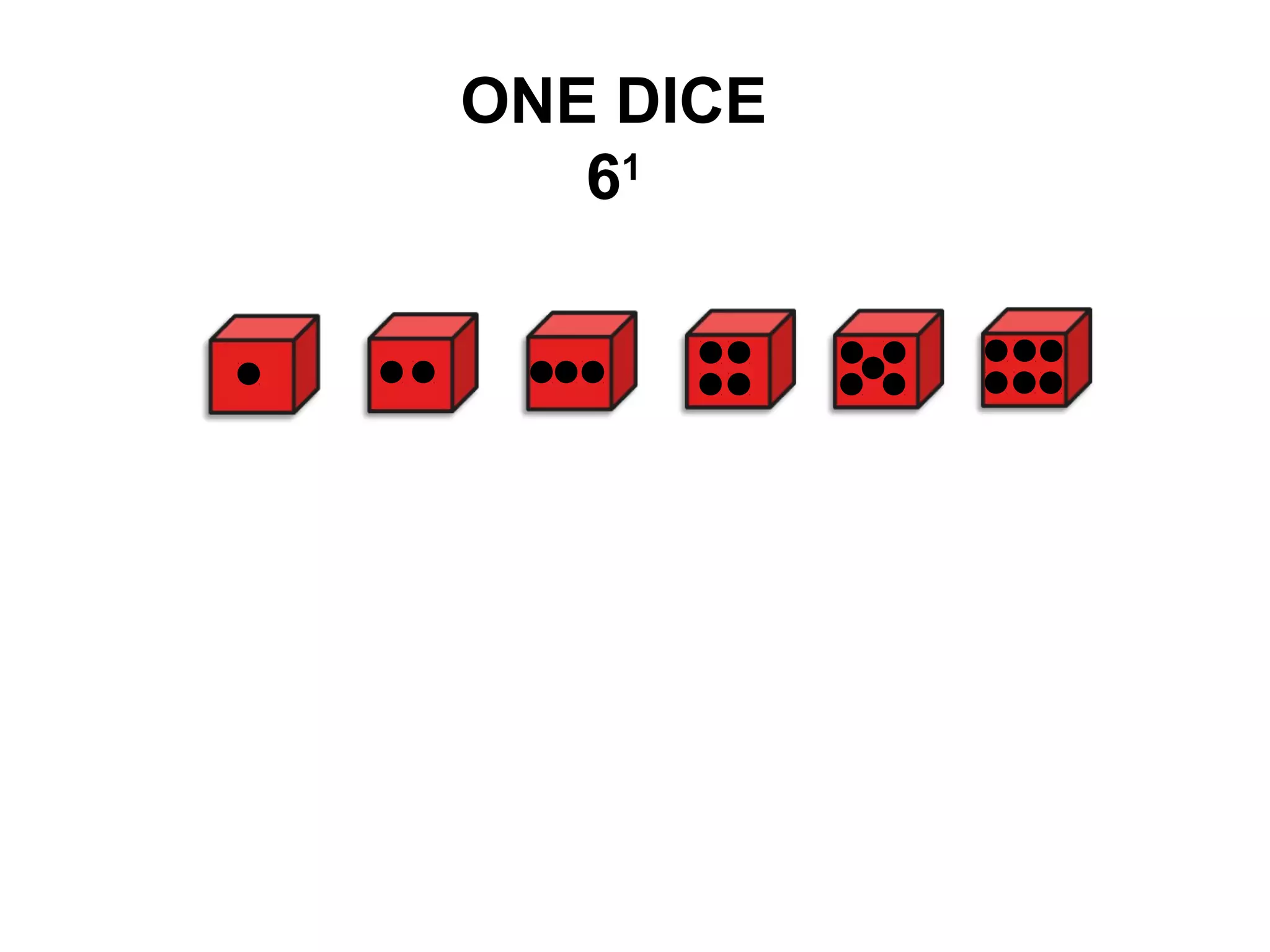
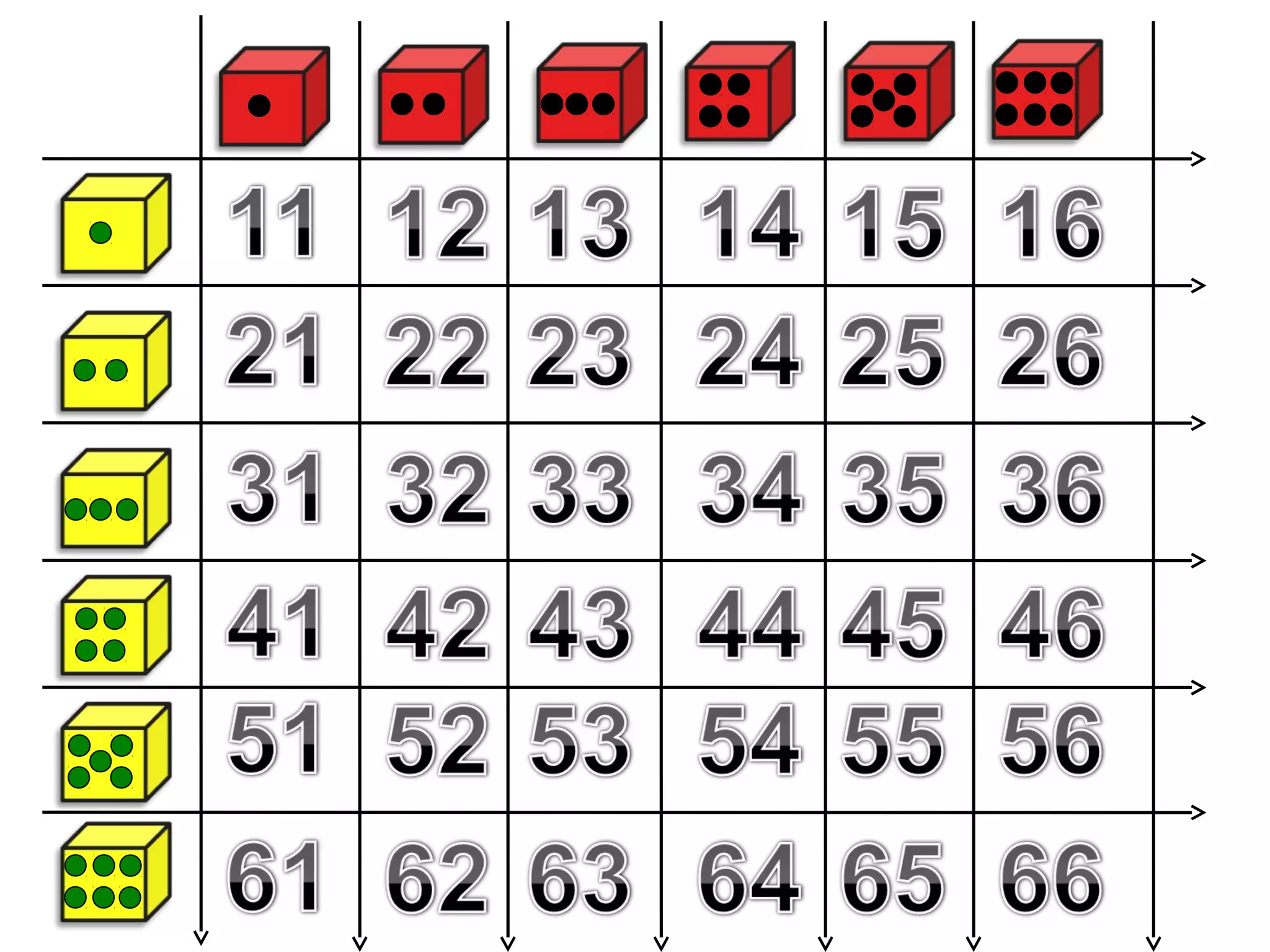
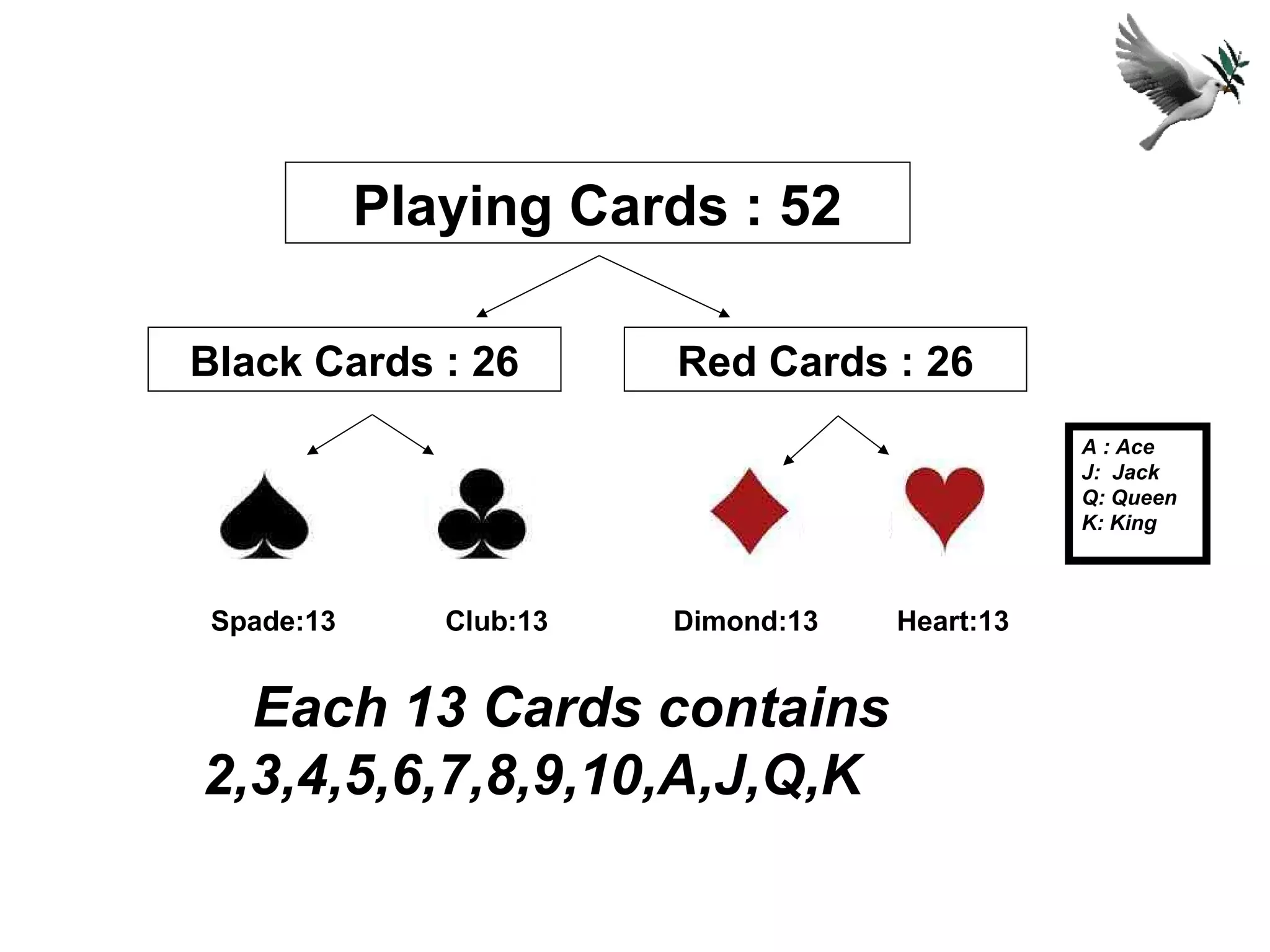
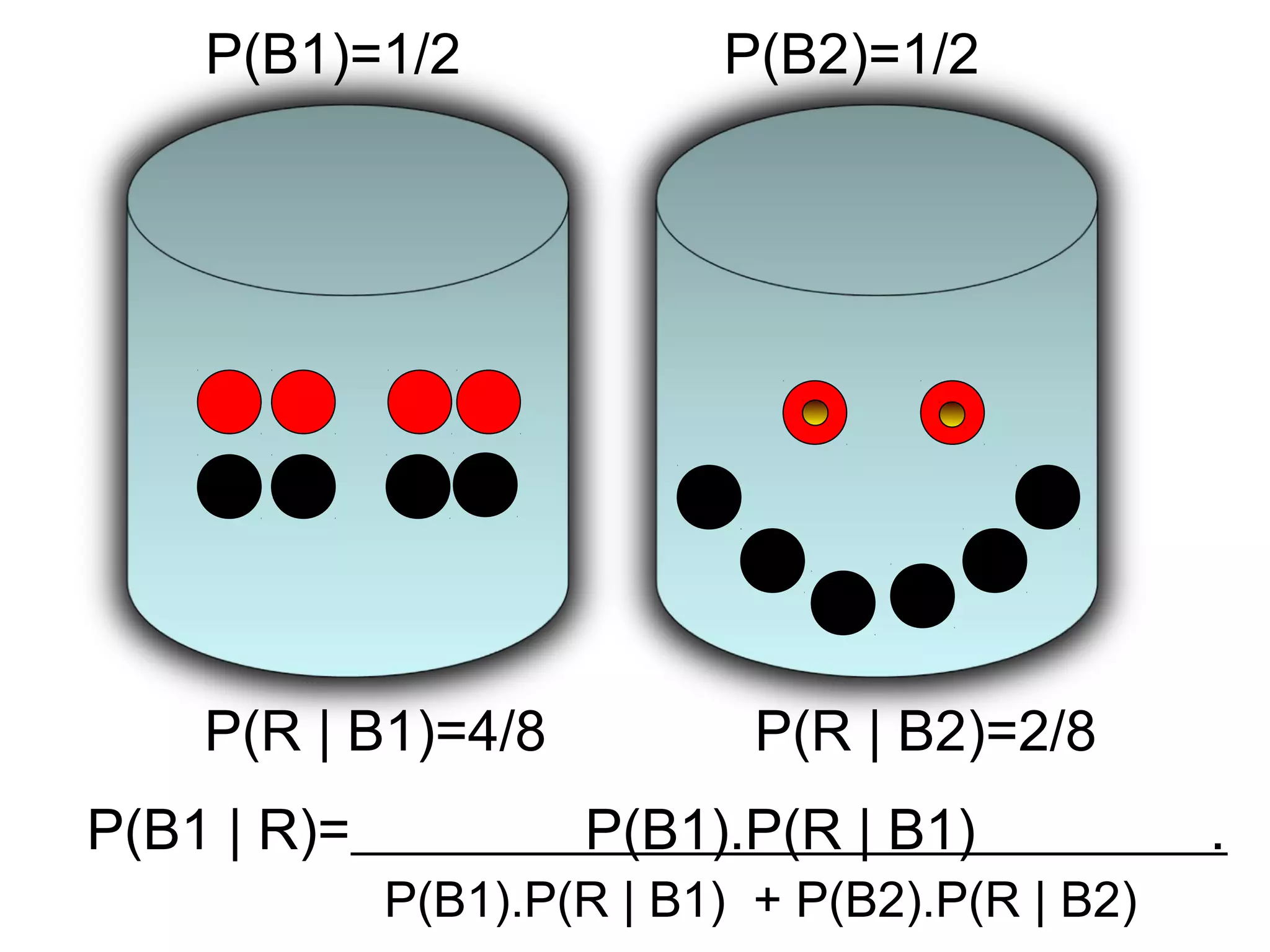
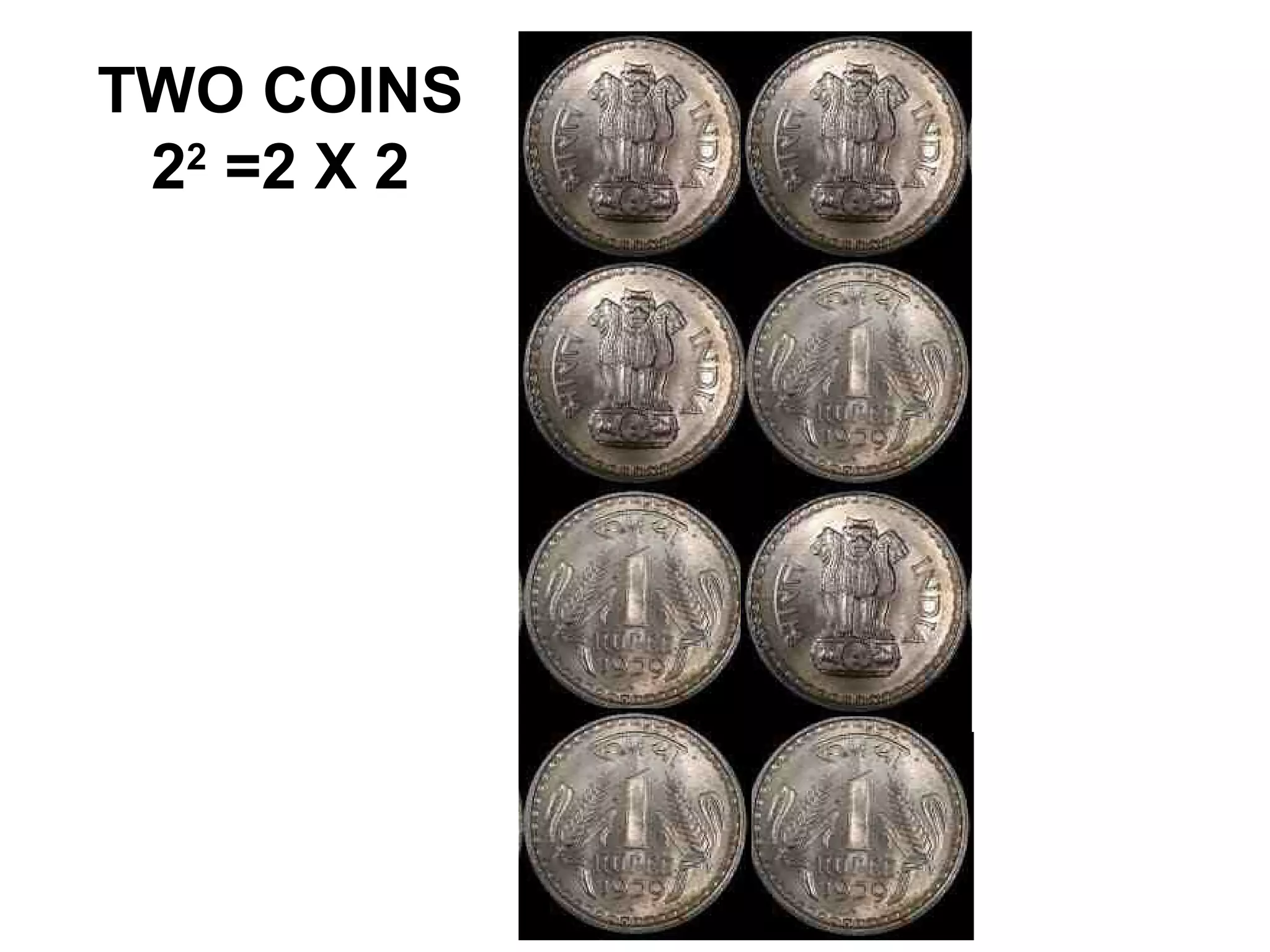This document provides an overview of probability theory and concepts. It was presented by P.N. Manjunath from Indira College of Education in Tumkur. The document defines key probability terms like random experiments, sample spaces, sample points, events, and the different types of events. It also provides examples of sample spaces for coin tosses, dice rolls, and playing cards. The document explains concepts like mutually exclusive and exhaustive events, and the algebra of events involving unions, intersections, and complements of events. It gives a problem on Bayes' theorem to calculate the probability a ball is drawn from the first bag.

1. PR BABILITY
C L A S S 10
Presentation by,
Manjunatha.P.N.
Indira college of education, Tumkur.

2. Theory of probability
Developed by Russian Mathematician
A.N. Kolmogorov in 1933
Approaches to Theory of probability
1.Statsistical approach
2.Classical approach

3. PROBABILITY
Probability is a measure of uncertainty
of various phenomenon.
We can find the probability on the basis of
observations and collected data. This is
called statistical approach of probability.

4. Define Random Experiment.
An experiment is called random
experiment if it satisfies the following two
conditions:
(i) It has more than one possible outcome.
(ii) It is not possible to predict the outcome
in advance.

5. Define Sample Space.
The set of all possible outcomes of a
random Experiment is called as Sample
space. It is denoted by S.
Define Sample points:
Elements of sample space are referred as
Sample points.
Define Event.
A subset of the sample space is called an
Event.

6. Impossible Event:
The empty set is called as Impossible
Event.
Sure Event:
The whole sample space is called as Sure
Event.
Types of Events:

7. Simple Event:
If an event E has only one sample
point of a sample space, it is called a
simple (or elementary) event.
Compound Event:
If an event has more than one sample
point, it is called a Compound event.
Types of Events:

8. ONE COIN
21

9. TWO COINS
22
=2 X 2

10. THREE COINS
23
= 2 X 2 X 2
H H H
H H T
H T H
H T T
T H H
T H T
T T H
T T T

11. ONE DICE
61

13. Playing Cards : 52
Black Cards : 26 Red Cards : 26
A : Ace
J: Jack
Q: Queen
K: King
Spade:13 Club:13 Dimond:13 Heart:13
Each 13 Cards contains
2,3,4,5,6,7,8,9,10,A,J,Q,K

16. PROBLEMS
In each of the following describe the sample space for the
indicated experiment.
1.A coin is tossed one time.
2.A coin is tossed two times.
3.A coin is tossed three times.
4.A coin is tossed four times.
5.A die is thrown one time.
6.A die is thrown two times.
7.A coin is tossed and a die is thrown.
8.A coin is tossed and then a die is rolled only in case a
head is shown on the coin.
2
Faces

17. A bag contains 4 red and 4 black balls.
Another bag contains 2 red and 6 black
balls. One of the two bags is selected
at random and a ball is drawn from the
Bag which is found to be red. Find the
Probability that the ball is drawn from
The first bag.

18. P(B1)=1/2 P(B2)=1/2
P(R | B1)=4/8 P(R | B2)=2/8
P(B1 | R)= P(B1).P(R | B1) .
P(B1).P(R | B1) + P(B2).P(R | B2)

19. P(R | B1)=4/8 P(R | B2)=2/8
P(B1 | R)= P(B1).P(R | B1) .
P(B1).P(R | B1) + P(B2).P(R | B2)
P(B1 | R)= 1/2. 4/8 =4= 2 .
1/2. 4/8 + 1/2 . 2/8 6 3
Baye’s theorem

20. Complementary Event:
For every event A, there corresponds another
event A  called the Complementary Event to A.
It is also called the event ‘not A’.
The Event A or B:
Let A and B are two Events, then Event A or B
contains all those elements which are either in A
or in B
or in both.
Event ‘A or B’=A U B = {x : x∈A or x∈B}
Algebra of Events:

21. The Event A and B:
Let A and B are two Events, then Event A and B
contains all those elements which are common
to both A and B
Event ‘A and B’=A ∩ B = {x : x∈A and x∈B}
The Event ‘A but not B’:
Let A and B are two Events, then Event A but
not B contains all those elements which are in A
but not in B.
Event ‘A but not B’=A - B = A ∩ B .
Algebra of Events:

22. Two events A and B are called mutually
exclusive events if the occurrence of any
one of them excludes the occurrence of
the other event.
ie. Events A and B are said to be Mutually
Exclusive Events if A ∩ B=φ.
MUTUALLY EXCUSIVE EVENTS

23. Events E1, E2, ..., En are said to be exhaustive if
atleast one of them necessarily occurs whenever
the experiment is performed.
ie. Events A and B are said to be Exhaustive
Events if A U B=S.
Or
Events E1,E2,E3,…..En are Exhaustive Events if
E1 U E2 U E3 U ……U En =S.
EXHAUSTIVE EVENTS

24. PRESENTED BY
P.N.Manjunath