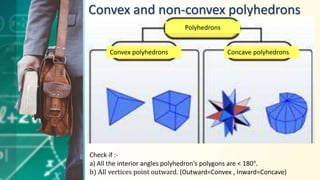
The document discusses the characteristics of two-dimensional (2D) and three-dimensional (3D) figures, defining 2D figures as plane shapes and 3D figures as solid shapes with length, breadth, and height. It classifies 3D objects into polyhedrons, which have flat surfaces, and non-polyhedrons, which have curved surfaces, explaining their types such as convex and concave polyhedrons. Additionally, it introduces Euler’s formula, which relates the number of faces, vertices, and edges of polyhedra.

1. Visualizing solid
shapes
Elwin Binu

2. 2D and 3D figures
1. Two Dimensional Figures:
These are plane figures which just have measurements like
length and breadth.
Example: Rectangle, Square, etc.
2. Three Dimensional Figures:
These are solid figures which have measurements like
length, breadth, height.
Example: Cube, cuboid , etc.

3. 3D objects/Solid shapes

4. Two types of 3D objects
• Non-polyhedrons
3D objects which have a curved surface.
Eg. Cylinder, Cone, Sphere
• Polyhedrons
3D objects which are made of flat surfaces (polygons).
In geometry, a polyhedron is a three dimensional shape with flat
polygonal faces, straight edges and sharp corners or vertices.
The word polyhedron comes from the Classical Greek
πολύεδρον, as poly- + -hedron.
Eg. Everything else….
Like,

5. Types of polyhedrons
• All polyhedrons are classified based on
the characteristics of the polygons
associated with them.

6. Regular and Irregular polyhedrons
Based on regularity of the polyhedron’s polygon.
Based on number of faces meeting at each vertex being equal or not.

7. Some examples
All angles are
equal and all
sides in the
polygon are equal

8. Convex and non-convex polyhedrons
Convex polyhedrons Concave polyhedrons
Polyhedrons
Check if :-
a) All the interior angles polyhedron’s polygons are < 180°.
b) All vertices point outward. (Outward=Convex , Inward=Concave)

10. Regular and Irregular polyhedrons
REGULAR
• Equal sides and angles in its
polygon
• Same number of faces
converge at a vertex
IRREGULAR
• Unequal faces and sides in
its polygon
• Not the same number of
faces converge at a vertex

11. Convex and Non-Convex polyhedrons
Convex
• All interior angles are less than 180
degrees
• Two points on the surface of the
polygon can always be connected
without protruding the polygon
• All the vertices of the polygon will
point outwards, away from the
interior of the shape. Think of it as
a 'bulging' polygon.
Non-Convex
• At least one interior angle is
greater than 180 degrees
• Two points on the surface of the
polygon cannot always be
connected without protruding
the polygon
• At least one of its vertices will be
point inward, towards the
polygon.

12. The 5 regular, convex polyhedrons
• There are 5 finite convex regular polyhedra (the
Platonic solids), and four regular star polyhedra (the
Kepler–Poinsot polyhedra), making nine
regular polyhedra in all. In addition, there are five
regular compounds of the regular polyhedra.
Mr. Plato

13. Prisms and Pyramids
• Prisms and Pyramids are two important
members of the polyhedron family.
• Prisms have 1) identical parallel ends
(congruent base and top-Rectangles)
2) all faces flat
• Pyramids have one base and all other faces
triangles
• Prisms have two bases -- pyramids only have
one.
• Both are named based on their bases.

14. • Prisms have two bases, which can be
any polygon. All the other faces(lateral
faces) are rectangles.
• Named based on type of base.

15. • Pyramids have only one base, which
can be of any polygon. All the other
faces are triangles.
• Named after type of base.

16. Euler’s formula
• Euler’s formula states that the sum of
number of faces and vertices = the
number of edges + 2. F + V = E - 2
• So,
F + V – E = 2

17. Let’s try and prove his theory

18. LET’S REVISE
#revisiontime!

19. Types of polygons

21. Euler’s formula
• Euler’s formula states that the sum of
number of faces and vertices = the
number of edges + 2. F + V = E - 2
• So,
F + V – E = 2