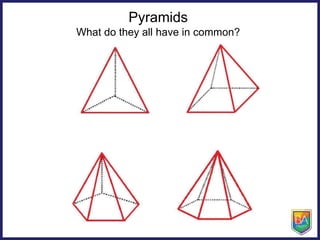
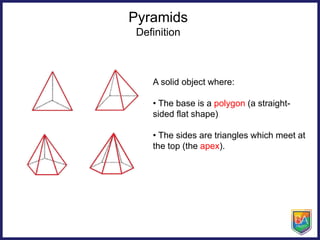
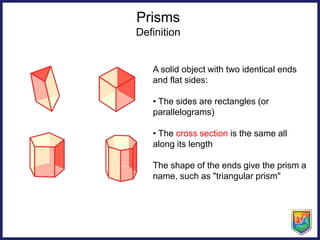
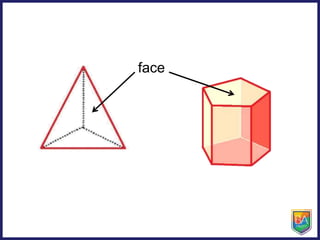
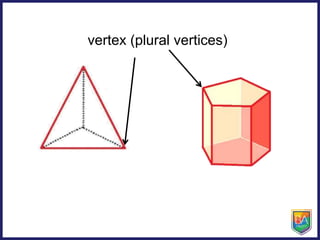
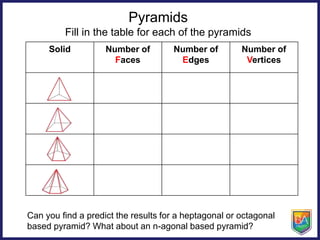
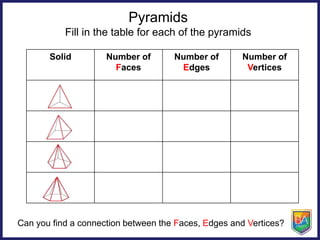
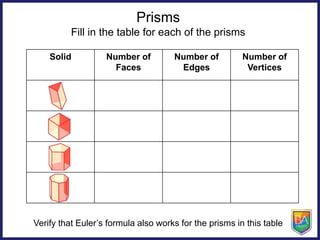
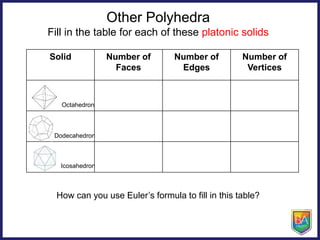
The document discusses pyramids, prisms, and other polyhedra like platonic solids. It defines pyramids and prisms, provides tables to fill in their numbers of faces, edges and vertices, and introduces Euler's formula relating these values. Euler's formula is said to be true for all polyhedra and can be used to fill in tables about the numbers of faces, edges and vertices of different solids. The document also asks why there are only 5 platonic solids.

1. Pyramids
What do they all have in common?

2. Pyramids
Definition
A solid object where:
• The base is a polygon (a straight-
sided flat shape)
• The sides are triangles which meet at
the top (the apex).

3. Prisms
What do they all have in common?

4. Prisms
Definition
A solid object with two identical ends
and flat sides:
• The sides are rectangles (or
parallelograms)
• The cross section is the same all
along its length
The shape of the ends give the prism a
name, such as "triangular prism"

5. face

6. edge

7. vertex (plural vertices)

8. Solid Number of
Faces
Number of
Edges
Number of
Vertices
Pyramids
Fill in the table for each of the pyramids
Can you find a predict the results for a heptagonal or octagonal
based pyramid? What about an n-agonal based pyramid?

9. Solid Number of
Faces
Number of
Edges
Number of
Vertices
Pyramids
Fill in the table for each of the pyramids
Can you find a connection between the Faces, Edges and Vertices?

10. Euler’s Formula for Polyhedra
V + F - E = 2.
The formula was discovered by
and bears the name of the
famous Swiss mathematician
Leonhard Euler (1707 - 1783)
It is true for all polyhedra.
(singular – polyhedron)

11. Solid Number of
Faces
Number of
Edges
Number of
Vertices
Prisms
Fill in the table for each of the prisms
Can you find a predict the results for a heptagonal or octagonal
prism? What about an n-agonal prism?

12. Solid Number of
Faces
Number of
Edges
Number of
Vertices
Prisms
Fill in the table for each of the prisms
Verify that Euler’s formula also works for the prisms in this table

13. Solid Number of
Faces
Number of
Edges
Number of
Vertices
Other Polyhedra
Fill in the table for each of these platonic solids
How can you use Euler’s formula to fill in this table?
Octahedron
Icosahedron
Dodecahedron

14. Why are there only 5 platonic solids?