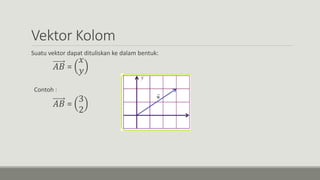
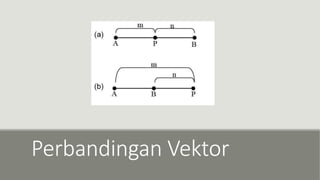
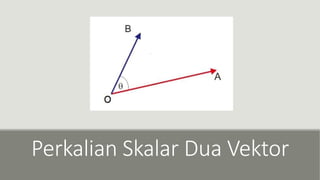
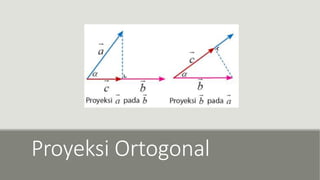
Dokumen ini menjelaskan konsep aljabar vektor, termasuk vektor kolom, panjang vektor, vektor satuan, dan operasional dasar seperti perkalian skalar. Rumus-rumus penting seperti perhitungan panjang vektor dan proyeksi ortogonal juga diuraikan. Selain itu, disediakan contoh aplikasi untuk memperjelas pemahaman tentang vektor dalam ruang R2 dan R3.

1. Aljabar Vektor
M. ZULFAN R.
X SC 2
SMA GLOBAL PRESTASI

2. Vektor di Bidang (R2)

3. Vektor Kolom
Suatu vektor dapat dituliskan ke dalam bentuk:
𝐴𝐵 =
𝑥
𝑦
Contoh :
𝐴𝐵 =
3
2

4. Panjang Vektor
Panjang suatu vektor kolom 𝐴𝐵 =
𝑥
𝑦 dapat dinotasikan dengan 𝑎 , dengan rumus :
𝐴𝐵 = 𝑥2 + 𝑦2 (Berdasarkan teorema phytagoras)
Contoh :
𝐴𝐵 =
3
4
, maka : 𝐴𝐵 = 32 + 42
𝐴𝐵 = 9 + 16
𝐴𝐵 = 25
𝐴𝐵 = 5

5. Vektor Satuan
Vektor satuan didefinisikan oleh :
𝑎 =
𝑎
𝑎
Dalam vektor kolom 𝐴𝐵 =
𝑥
𝑦 , maka : 𝑎 =
1
𝑥2+𝑦2
×
𝑥
𝑦
Karena 𝑎 =
𝑎
𝑎
, maka
vektor kolom ( 𝑎) = vektor satuan ( 𝑎) × panjang vektor ( 𝑎 )

6. Persamaan Vektor dari Sebuah Garis Lurus
Gambar di samping menunjukkan garis 𝑘 melalui titik A
dengan arah 𝑝, jika terdapat titik R pada garis 𝑘, perpindahan
vektor 𝐴𝑅 dapat dituliskan dengan :
𝑟 = 𝑎 + 𝑡 𝑝

7. Vektor di Ruang (R3)

8. Panjang Vektor
Panjang vektor pada ruang (R3) dapat dinotasikan dengan rumus :
𝐴𝐵 = (𝑥2 − 𝑥1)2+(𝑦2 − 𝑦1)2+(𝑧2 − 𝑧1)2

9. Perbandingan Vektor

10. Perbandingan Vektor
Pembagian dalam bentuk vektor dIrumuskan dengan :
𝑟 =
𝑚𝑏 + 𝑛 𝑎
𝑚 + 𝑛

11. Perkalian Skalar Dua Vektor

12. Perkalian Skalar Dua Vektor
Perkalian skalar dari 𝑎 dan 𝑏 dapat dirumuskan dengan :
𝑎 ⋅ 𝑏 = 𝑎 𝑏 cos 𝜃
Jika 𝑎 = 𝑎1 𝑖 + 𝑎2 𝑗 + 𝑎3 𝑘 dan 𝑏 = 𝑏1 𝑖 + 𝑏2 𝑗 + 𝑏3 𝑘, maka hasil kali skalar dua vektor
dirumuskan dengan :
𝑎 ⋅ 𝑏 = 𝑎1 𝑏1 + 𝑎2 𝑏2 + 𝑎3 𝑏3
Dari rumus 𝑎 ⋅ 𝑏 = 𝑎 𝑏 cos 𝜃, maka :
cos 𝜃 =
𝑎⋅𝑏
𝑎 𝑏
𝜃 = cos−1 𝑎⋅𝑏
𝑎 𝑏

13. Proyeksi Ortogonal

14. Proyeksi Ortogonal Suatu Vektor kepada
Vektor Lain
PROYEKSI SKALAR
Dirumuskan dengan :
𝑎 𝑏 =
𝑎 ⋅ 𝑏
𝑏
atau
𝑐 =
𝑎 ⋅ 𝑏
𝑏
PROYEKSI VEKTOR
𝑎 𝑏 = 𝑝𝑟𝑜𝑦𝑒𝑘𝑠𝑖 𝑠𝑘𝑎𝑙𝑎𝑟 ⋅ 𝑣𝑒𝑘𝑡𝑜𝑟 𝑠𝑎𝑡𝑢𝑎𝑛 𝑏
𝑎 𝑏 = 𝑎 𝑏 ⋅
𝑏
𝑏
atau
𝑎 𝑏 =
𝑎⋅𝑏
𝑏 2 ⋅ 𝑏

15. Thank You