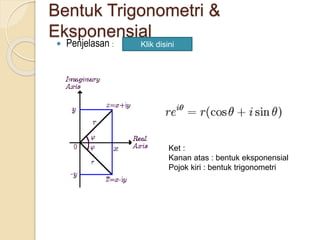
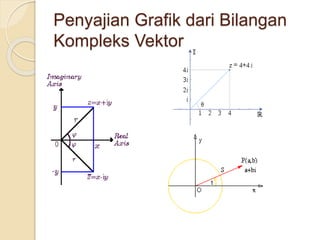
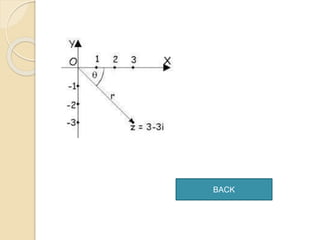
Dokumen ini membahas tentang bilangan kompleks, termasuk komponen, ekspresi dalam berbagai bentuk, dan operasi hitung seperti penjumlahan, pengurangan, perkalian, dan pembagian. Selain itu, juga dijelaskan tentang bentuk polar, rumus Euler, serta hubungan antara bilangan kompleks dan aplikasi dalam rangkaian listrik. Terdapat pula konsep nilai mutlak dan teori De Moivre dalam konteks grafik.

1. VARIABEL KOMPLEKS DAN
APLIKASINYA
OLEH
•Arief Betta K (062.10.015)
•Anggita Mentari Putri M (062.13.004)
•Nur Fitryah (062.13.009)
•Vera Irene Martina R (062.13.007)

2. Bilangan Kompleks
• Bilangan Kompleks adalah bilangan yang besaran
(skalarnya) tidak terukur secara menyeluruh.
• 2 komponen Bilangan Kompleks :
– Bilangan Nyata (riil)
– Bilangan Khayal (imajiner)
 Bilangan kompleks merupakan fasor( vektor yang
arahnya ditentukan oleh sudut fasa)
 Bilangan Kompleks dapat diekspresikan dalam 4
bentuk, yaitu : bentuk rectangular, bentuk polar,
bentuk trigonometri, dan bentuk eksponensial

3.  Bentuk umum : Z = a + ib
 Operasi hitungan pada Bilangan Kompleks :
◦ Penjumlahan : ( a+ib) + (c+id) = (a+c) + i(b+d)
◦ Pengurangan : (a+ib) – (c+id) = (a-c) + i(b+d)
◦ Perkalian : (a+ib) (c+id) = ac + adi + bci + bdi
= (ac-bd) + i(ad+bc)
◦ Pembagian : (a+ib)/(c+id) = (a+ib)/(c+id) * (c-id)/(c-id)
= (ac-iad +ibc-i²bd)/(c²-i²d²)
= (ac+bd+i(bc-ad))/(c²+d²)
= (ac+bd)/(c²+d²) + i(bc-ad)/(c²+d²)
◦ Kenapa I² = -1? Penjelasan…
Bila √(-1) = i atau √(-1) = j, maka i² = [√(-1)].[√(-1)] = -1
◦ Kompleks sekawan : bila Z = a+ib, maka Ž = a-ib
◦ Nilai Mutlak : |Z| = √(a²+b²)
 |Z1.Z2| = |Z1| |Z2|
 |Z1/Z2| = |Z1| / |Z2|
 |Z1 + Z2| ≤ |Z1|+|Z2|
 |Z1 + Z2| ≥ |Z1|-|Z2|

4. Bentuk Polar
 Dalam koordinat polar : X = r cos ø
Y = r sin ø
 Z = r ( cos ø + isin ø)
= r cis ø = r e iø
 Rumus Euler : e iø = cos ø + isin ø
 R adalah modulus dari Z. r = |Z|
 Ø = argumen dari Z, ditulis dengan arg Z.
◦ Arg Z = θ = Arc tan (X/Y)
= Arc sin (/R)
= Arc cos (X/Z)
Contoh soal Klik disini

5. Bentuk Trigonometri &
Eksponensial
 Penjelasan : Klik disini
Ket :
Kanan atas : bentuk eksponensial
Pojok kiri : bentuk trigonometri

6. Penyajian Grafik dari Bilangan
Kompleks Vektor

7. Dalil de Moivre
Contoh soal

8. CONTOH SOAL DAN PENYELESAIAN
APLIKASI VARIABEL KOMPLEKS KE
RANGKAIAN LISTRIK
PENJELASAN APLIKASI VARIABEL
KOMPLEKS KE RANGKAIAN LISTRIK
END

9. BACK

10. BACK

11. BACK