1) The paper proposes a technique to efficiently analyze large spatio-temporal urban data sets and automatically detect meaningful events using topological analysis. 2) It designs an indexing scheme to group similar event patterns across time slices and a visual interface to guide exploratory analysis. 3) Case studies on NYC taxi and subway data demonstrate how the technique can identify irregular traffic events like parades as well as regular hot spots and delay patterns to support analysis of these urban systems.

1. Using Topological Analysis to Support
Event-Guided Exploration in Urban Data
IEEE transactions on visualization and computer graphics
Harish Doraiswamy, Nivan Ferreira, Theodoros Damoulas, Juliana Freire and Cl´audio T. Silva

2. Overview of the paper
• Motivation
 To examine prohibitively large number of spatio-temporal slices in efficient way
and discover interesting patterns from it
• Contribution
 Propose an efficient and scalable technique that automatically discovers events
 Guide users towards potentially interesting data slices
 Accomplish event detection through the application of topological analysis on a
time-varying scalar function
 Design an indexing scheme that groups similar patterns across time slices
 Design visual interface to aid in event-guided exploration of urban data
1

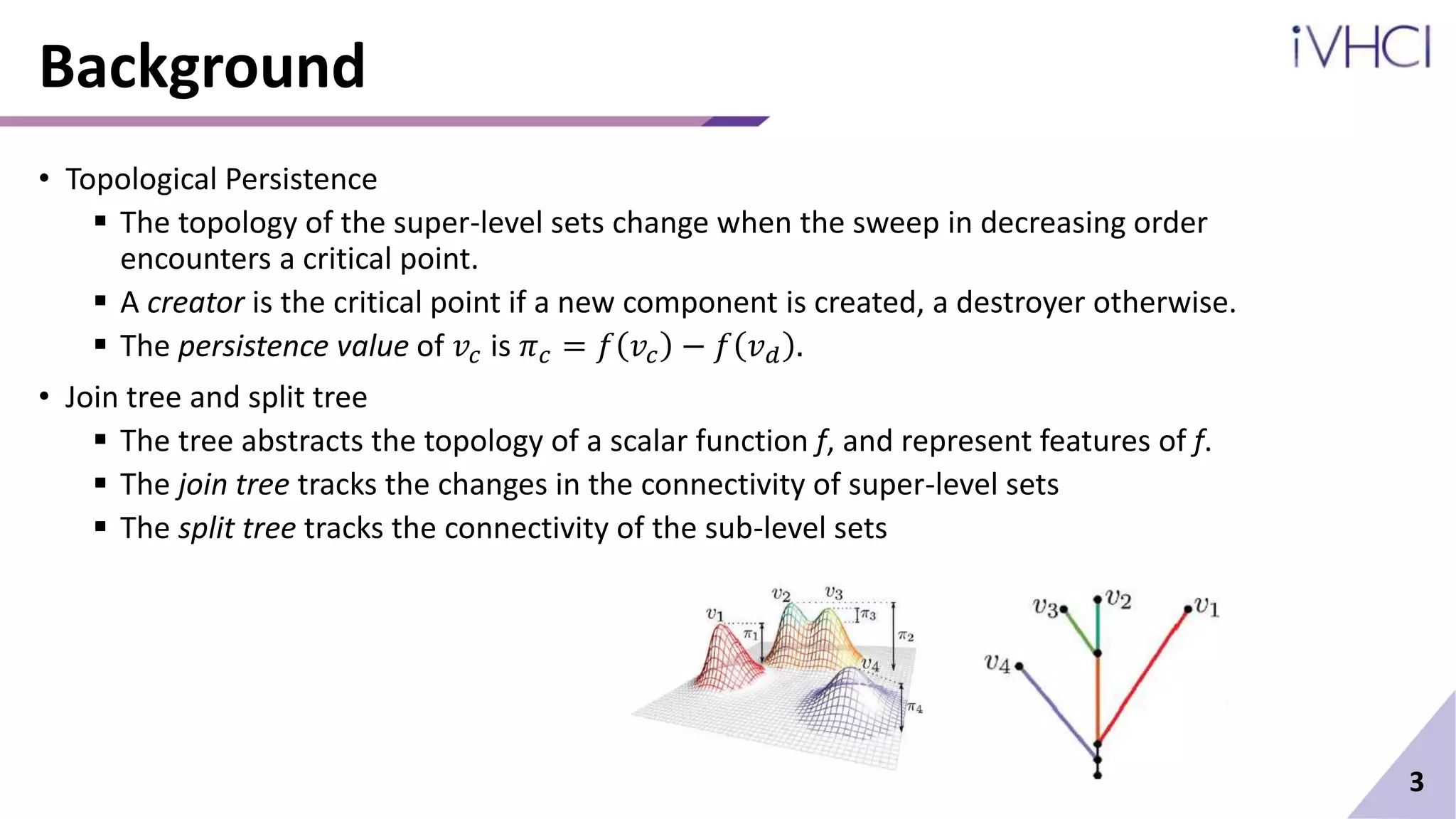
3. Background
• A scalar function maps points in a spatial domain.
 The function value at each point on this graph is equal to the point’s y-coordinate.
• A super-level set of a real value a is the pre-image of the interval [a,+∞).
• A sub-level set of a is the pre-image of the interval (−∞,a].
• Critical points of a smooth real-valued function are exactly where the gradient becomes zero.
 Topological changes occur at critical points.
 A maximum captures a peak of the function, where the function value is higher than its
neighborhood.
 A minimum captures a valley of the function.
• Regular points are the points that are not critical.
 Topology of the super-level (sub-level) set is preserved across regular points.
2

4. Background
• Topological Persistence
 The topology of the super-level sets change when the sweep in decreasing order
encounters a critical point.
 A creator is the critical point if a new component is created, a destroyer otherwise.
 The persistence value of 𝑣𝑐 is 𝜋𝑐 = 𝑓 𝑣𝑐 − 𝑓 𝑣𝑑 .
• Join tree and split tree
 The tree abstracts the topology of a scalar function f, and represent features of f.
 The join tree tracks the changes in the connectivity of super-level sets
 The split tree tracks the connectivity of the sub-level sets
3

5. Data
• NYC Taxi Data
 Manhattan during 2011 and 2012
 Each trip consists of pickup and drop-off locations and times
 Average 500 thousand trips each day
 Identifying road closures and taxi hot spots
 Scalar function for an hourly interval at each node of this graph as the density of taxis
within a small circular region
 Minima and maxima are used to represent events
• MTA Subway Data
 Time stamps of all the stops for all the trips that happen each day.
 Delays in the schedule of the different trains ( scheduled – actual)
 The nodes of this path corresponds to the different stations along its route
4

6. Managing Events
• Computing Events
1. Split tree to see the significant events
2. Persistence to capture the importance of a feature
3. Geometric size of a feature to consider the characteristic of hyper-volume
4. Remain top-k from the set of minima
• Event Group Index
 Define a notion of similarity between events based on their geometric and topological
properties
 Group similar events within a certain time interval into event groups
 Define a key to index these groups
5

7. Event Group Index
• Similarity Between Events
 E is formally represented as a pair (R, τ)
• R is a subgraph of spatial region
• τ is a real number representing topological importance
 Graph distance metric δ, to measure the geometric similarity between R1 and R2
δ 𝐸1, 𝐸2 = 1 −
|𝑅1 ∩ 𝑅2|
max( 𝑅1 , 𝑅2 )
• 𝑅1 ∩ 𝑅2 denotes the maximum common subgraph between R1 and R2
• 𝑅 denotes the number of nodes in R
• Measures the amount of overlap between two regions, ensuring that similar regions have a significant
overlap
 Topological similarity between two events
T 𝐸1, 𝐸2 = |τ1 − τ2|
• Two events E1 and E2 are similar if δ 𝐸1, 𝐸2 ≤ εδ and τ 𝐸1, 𝐸2 ≤ ετ
• Ensures that the two events are topologically close with respect to the topological importance
6

8. Event Group and Event Group Key
• Use a time period equal to one month
 not to miss periodic events
 not to create a computational bottleneck
• Given an event group Σ = 𝐸1, 𝐸2, … , 𝐸𝑘 , define the event group key of Σ as (𝑅Σ, τΣ)
𝑅Σ =
𝑖∈[1,𝑘]
𝑅𝑖 𝑎𝑛𝑑 τΣ =
𝑖=1
𝑘
τ𝑖/𝑘
• 𝑅𝛴 is the maximum common subgraph of the geometric regions  overlap for similarity condition
• τΣ captures average of the topological importance
• Follows definition of geometric and topological similarity measures
• The definition of event group key helps in using a consistent definition for the similarity between event
groups
• When two similar event groups are found, they are merged into a single group
• With given query, perform a linear search over the set to find events
7

9. Visual Exploration Interface
• Map View and Query Interface
• Event Group Distribution View and Timeline View
 Range is the amount of time between the first and the last event
 Density is the number of events of group that happen per time unit
• Classification of event groups with two attributes
 Region I:
• Low range, but high density
• Rare occurrence (irregular pattern)
 Region II:
• High range and high density
• Occur over frequent periods, so can identify trend
 Region III:
• Small number of events that span a large range
• Potentially represent patterns that are regular over a large time interval
• Irregular with respect to the range of the input data
 Region IV:
• Low range as well as low density
8
Filtering Interface
Event group size
Event size
Event time
Spatial region

10. Case Studies – NYC Taxi data
• To help them identify areas with high concentrations of taxis
• Minima events in NYC
 Regions where there are comparatively fewer taxis
• If this place is usually a high density of taxis, blockage of streets
• Hourly events
 Sixth avenue in Greenwich Village on October 31st
 This corresponds to the annual NYC Halloween Parade
• Daily events
 Fifth avenue on October 9th and 10th, 2011
 This corresponds to the Hispanic Day Parade on 9th October and the
Columbus Day Parade on October 10th
• Weekly events
 NYC Summer streets that happens on Park avenue
 Occurred on three consecutive Saturdays, 6th, 13th, and 20th
August respectively
9

11. Case Studies – NYC Taxi data
• Querying events
 Search for events similar to a selected event that occurs in other
months
 find other parades that also occurred in the same location.
• Identifying trends
 Maxima events show high concentration of taxis
 If such concentrations are frequent, then it could imply taxi hot spots
 Optimize the amount of receiver place
10

12. Case Studies – MTA data
• To identify events related to delays
• The amount of delay is applied as topological persistence for
importance measure
• Minimum event groups
 Find a station at which the delay is lower than that of its neighbors
 Signals where trains start to get delayed
 Frequent presence of such events are in Region II
 Wall Street station
• Events occur predominantly during the rush hour period on
weekdays
 14th street station
• 3 train sometimes waits for the 1 train
11

13. Limitation and Future work
• The characteristic of the event is not explainable unless the user search the event
• The system should iterate the group to find the similar event
• No entire view of the system other than the graphs
• Scalar function should be assigned considerately
• Speed can be used for scalar function computation
12