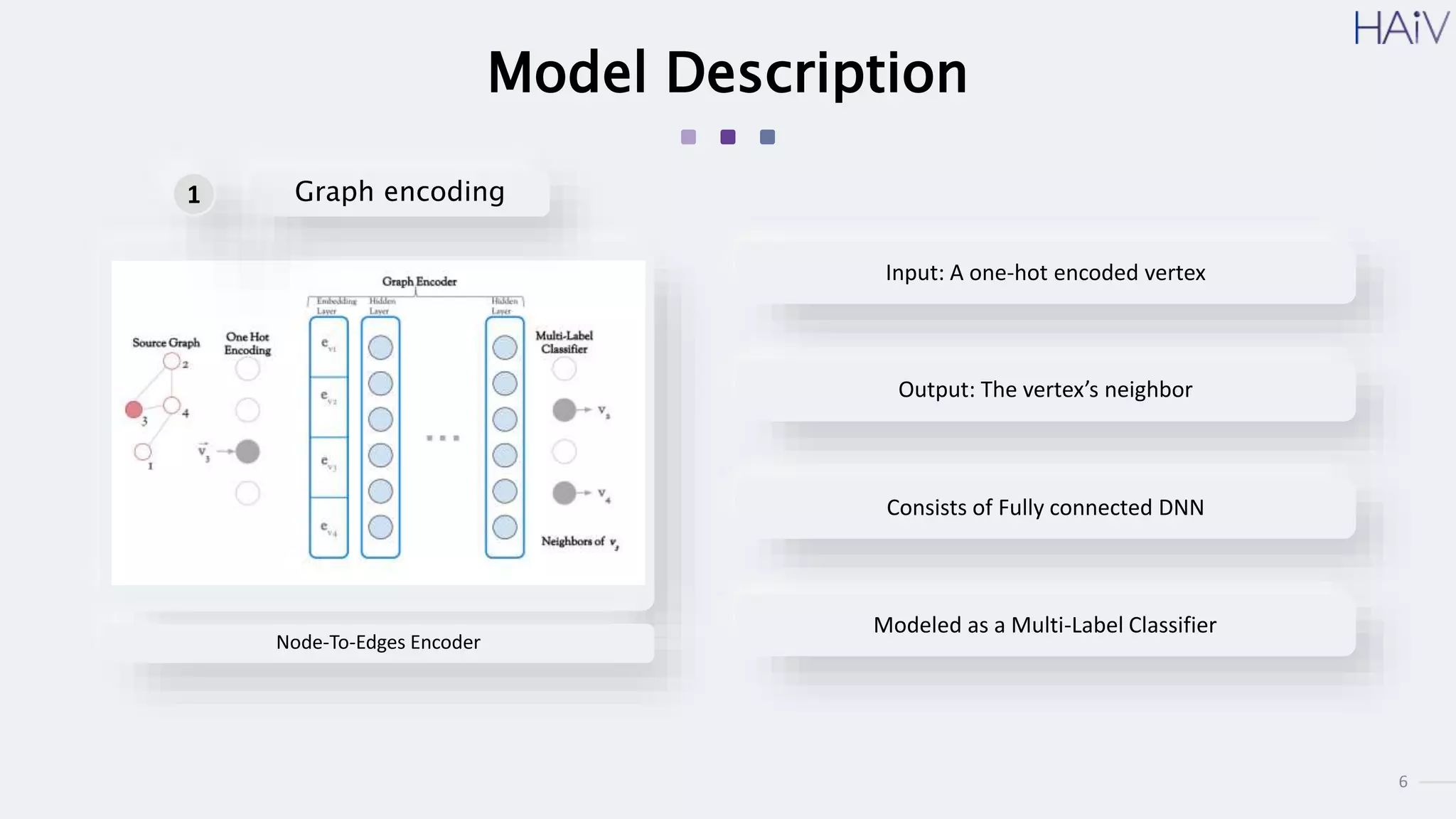
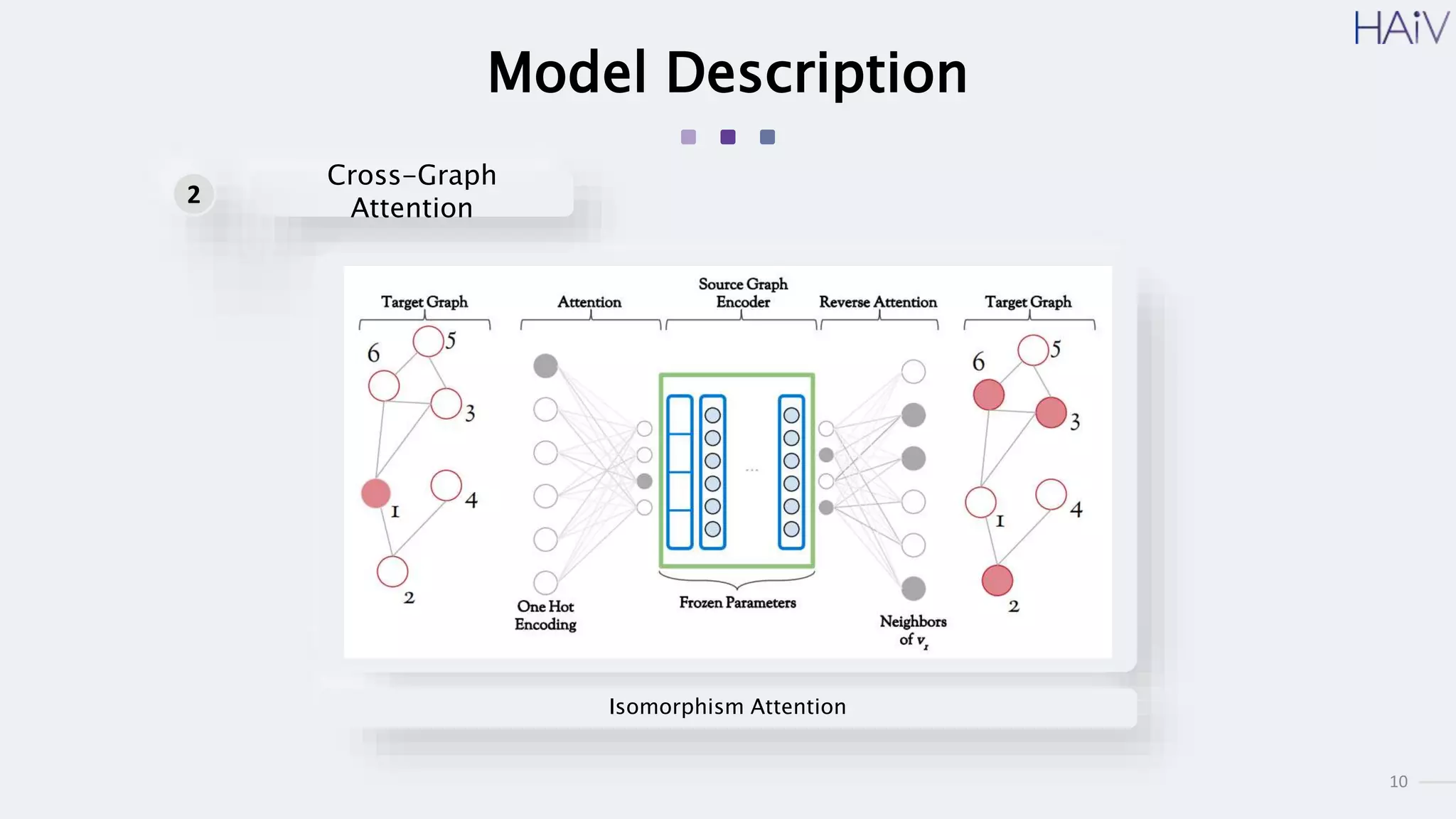
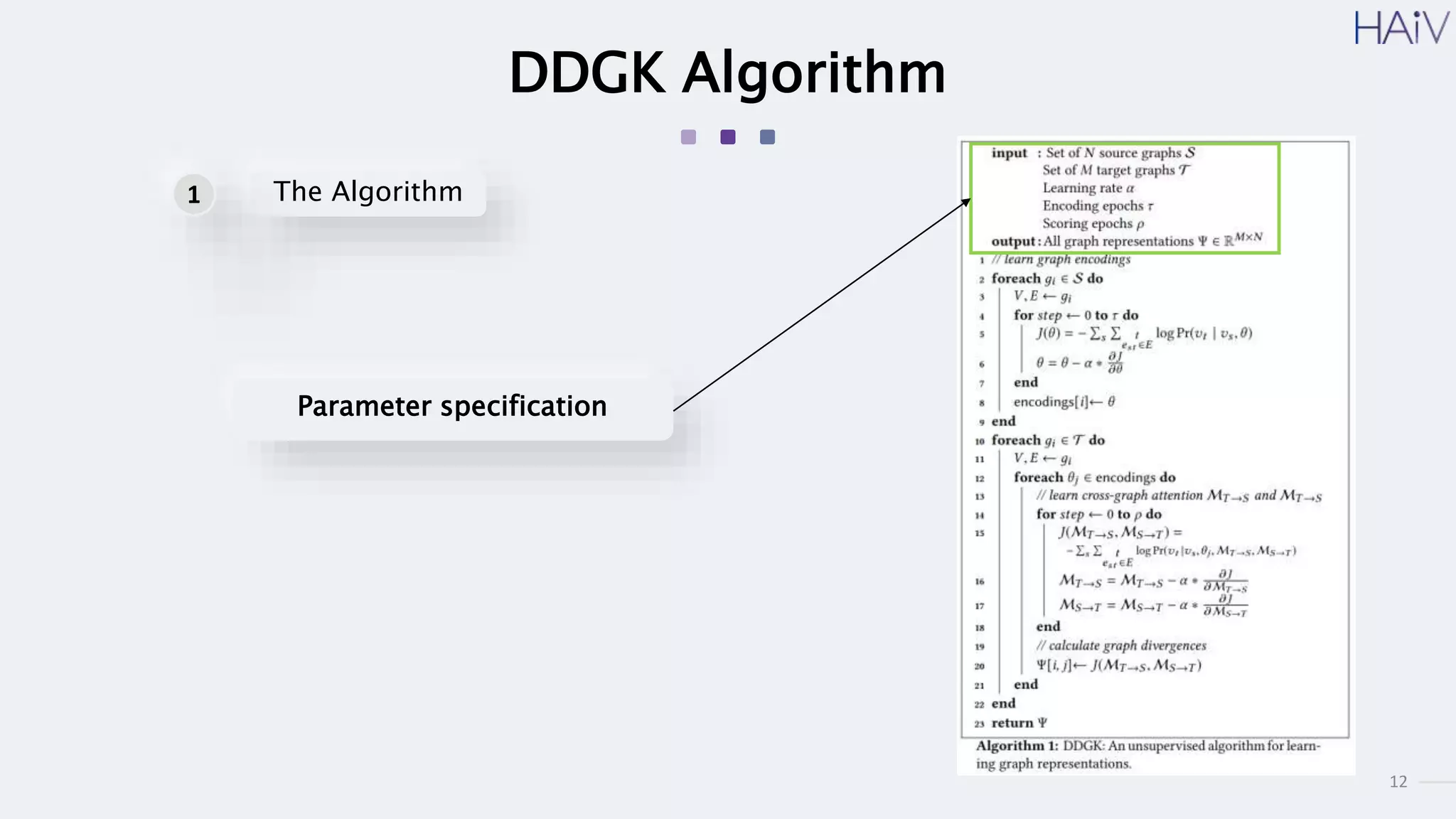
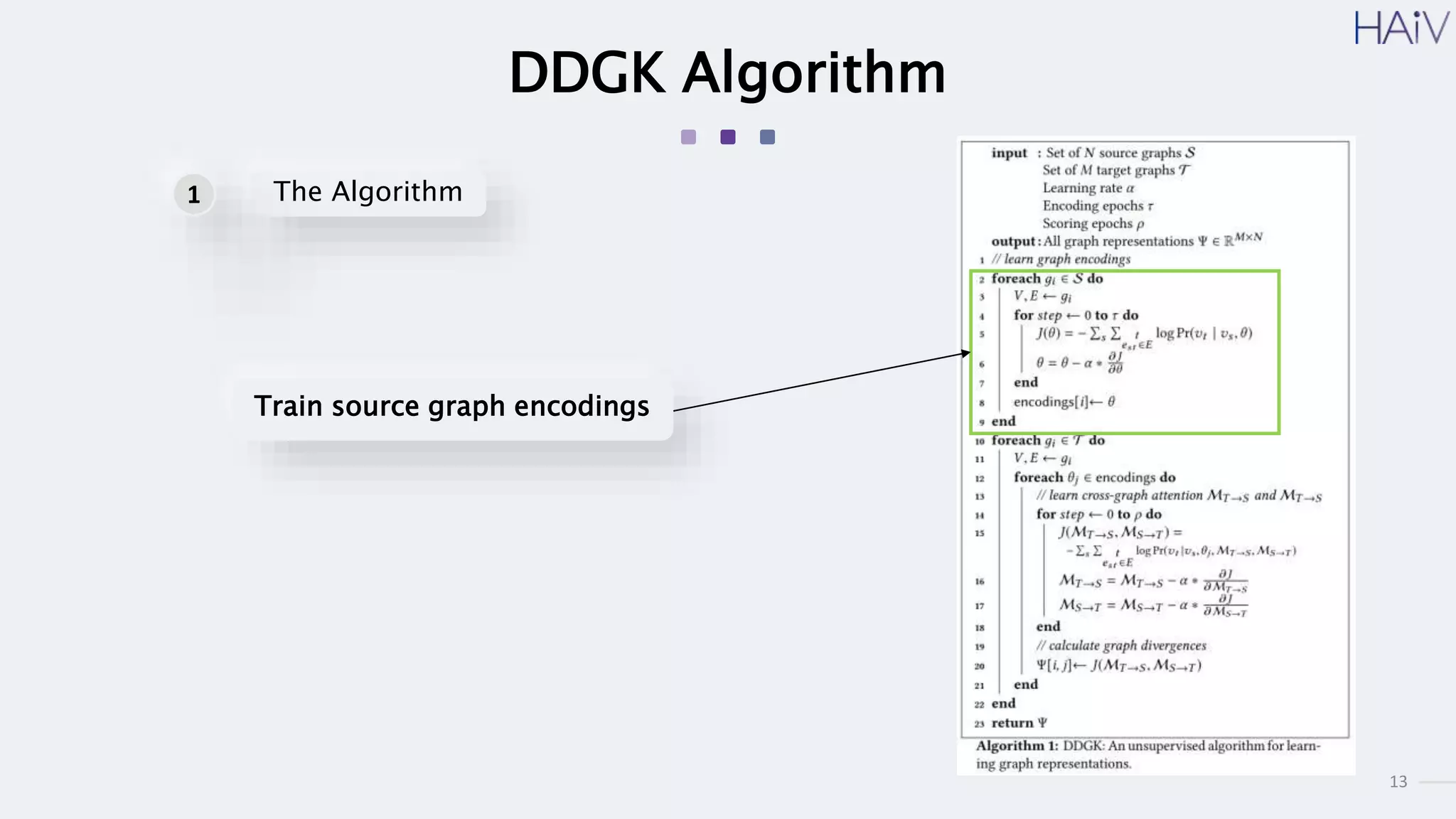
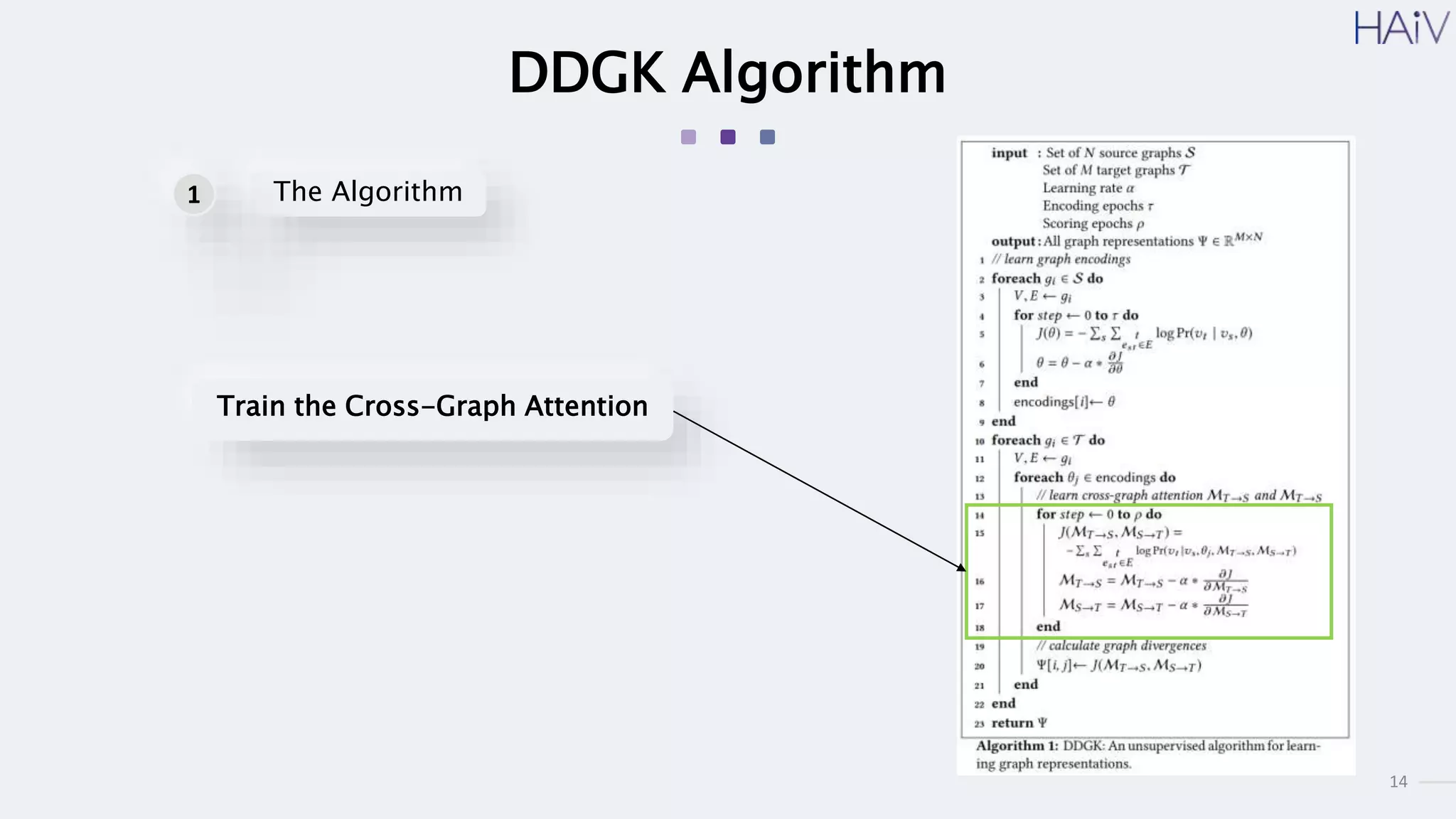
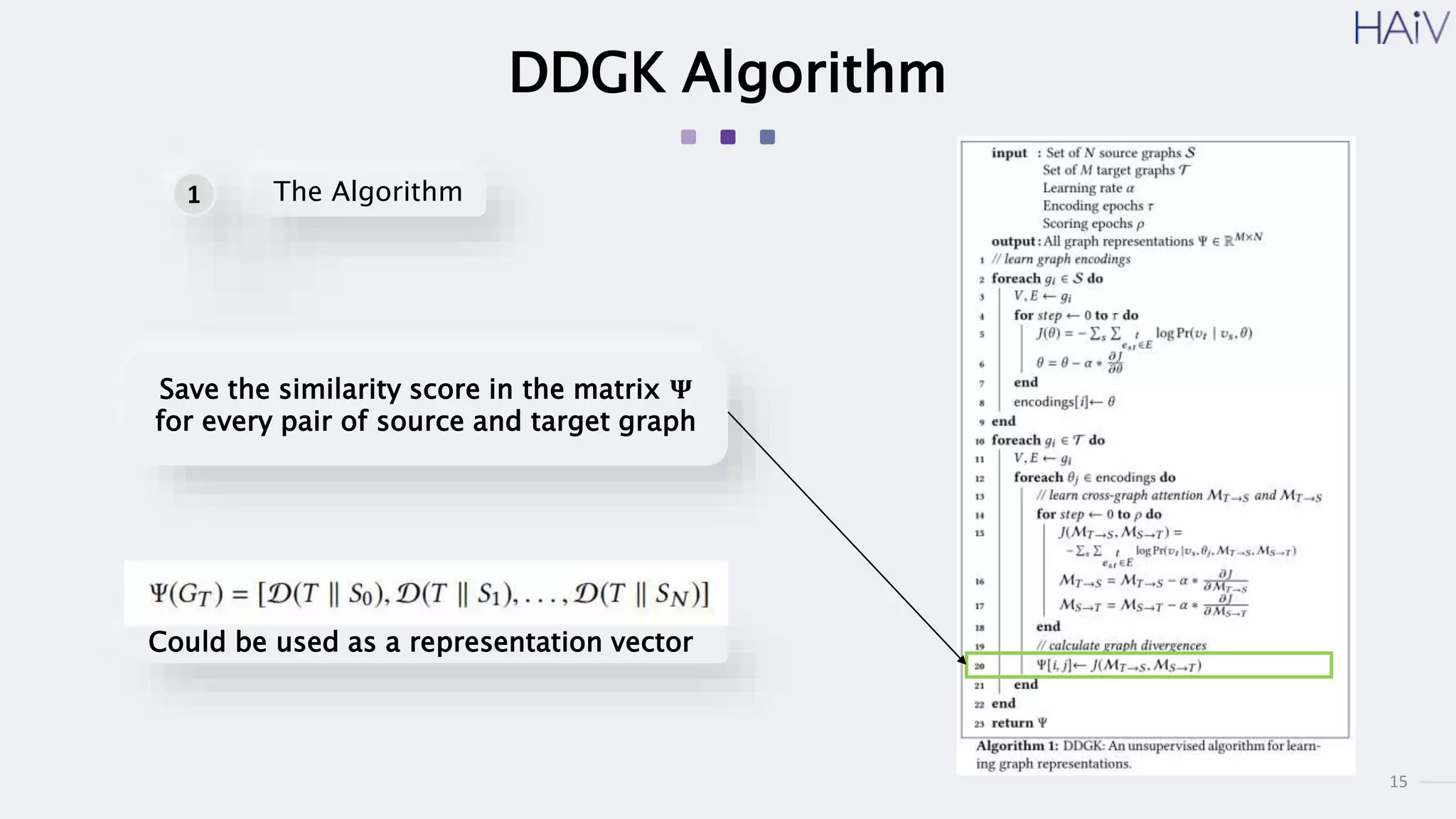
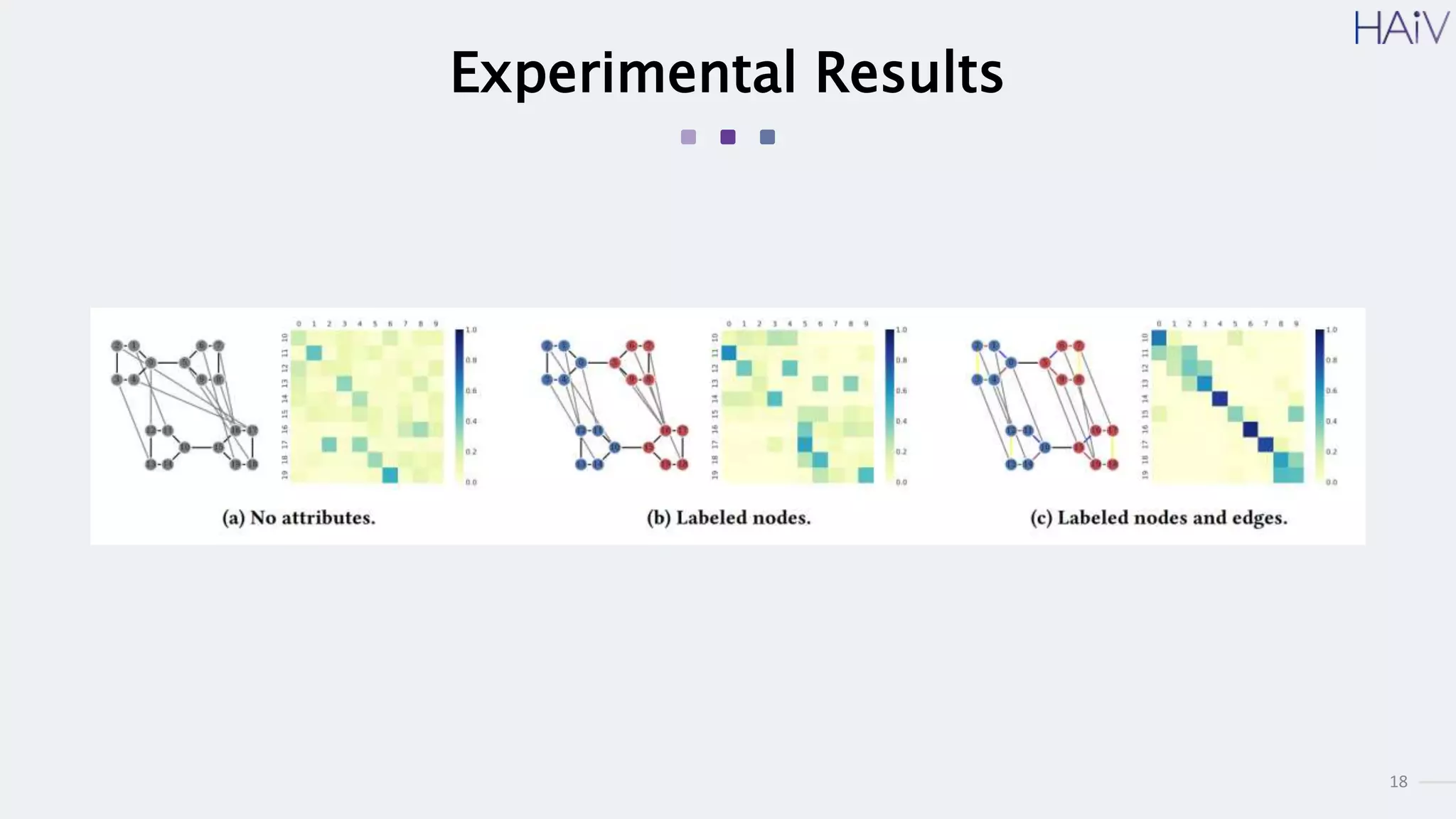
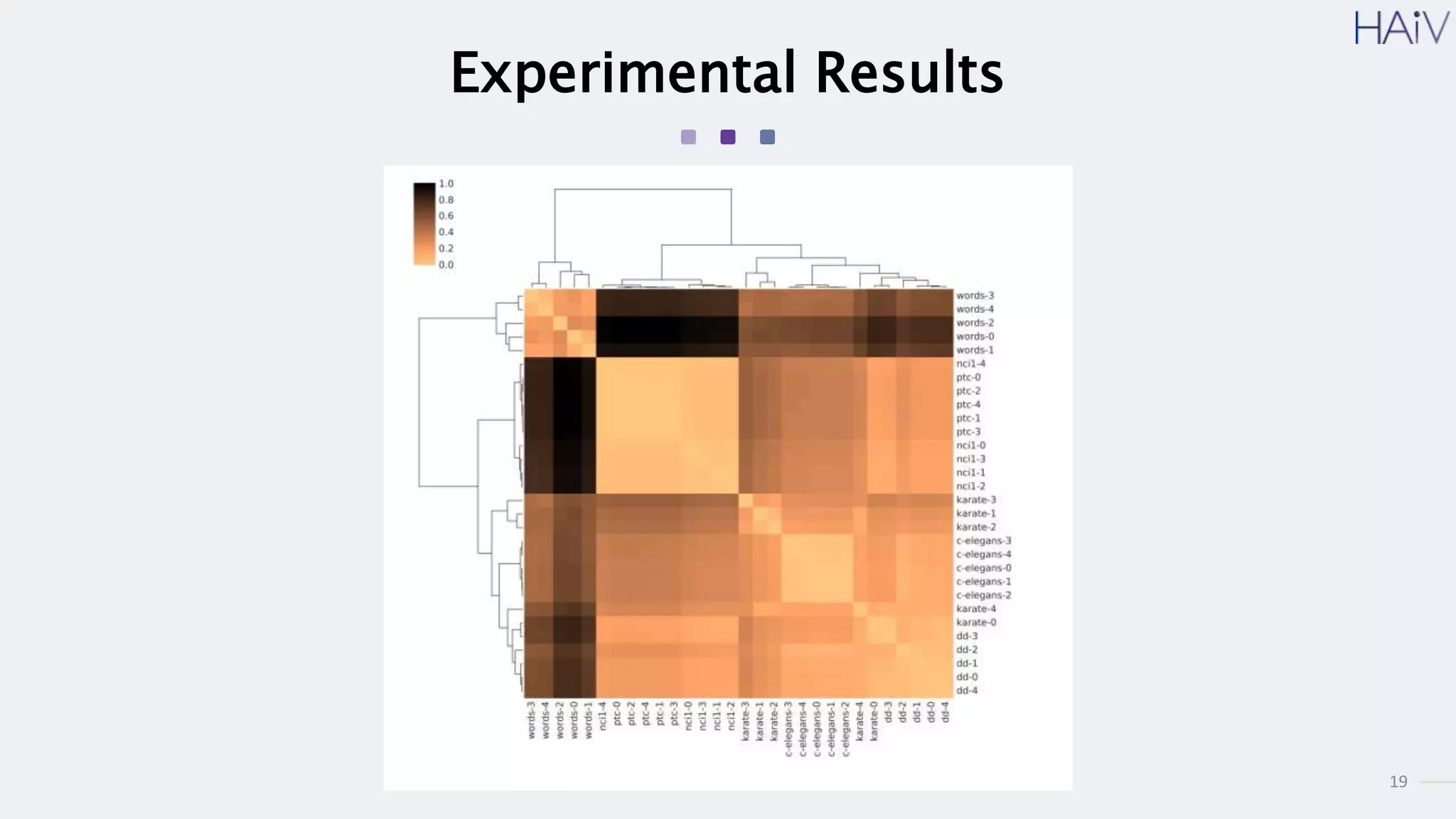
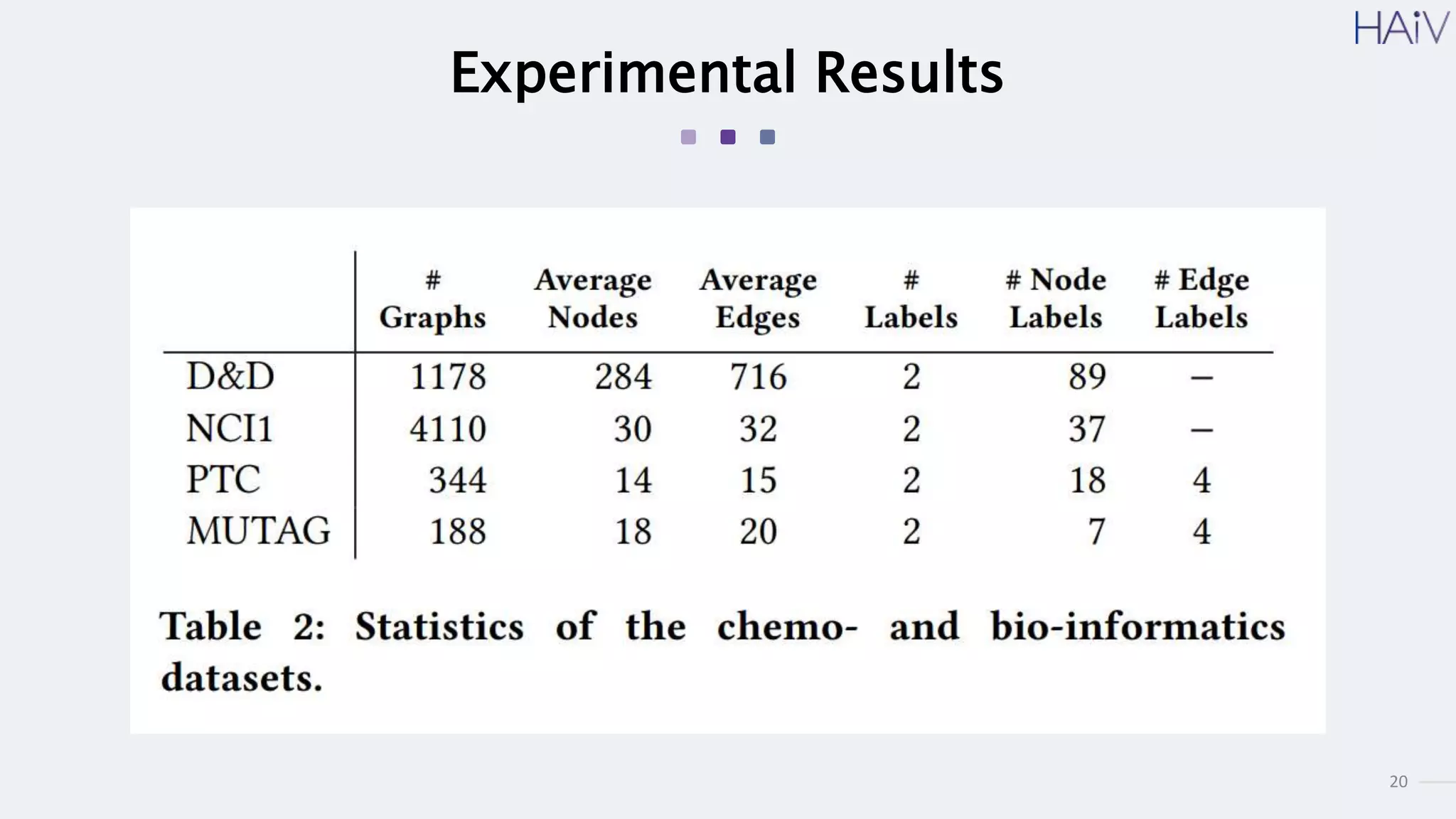
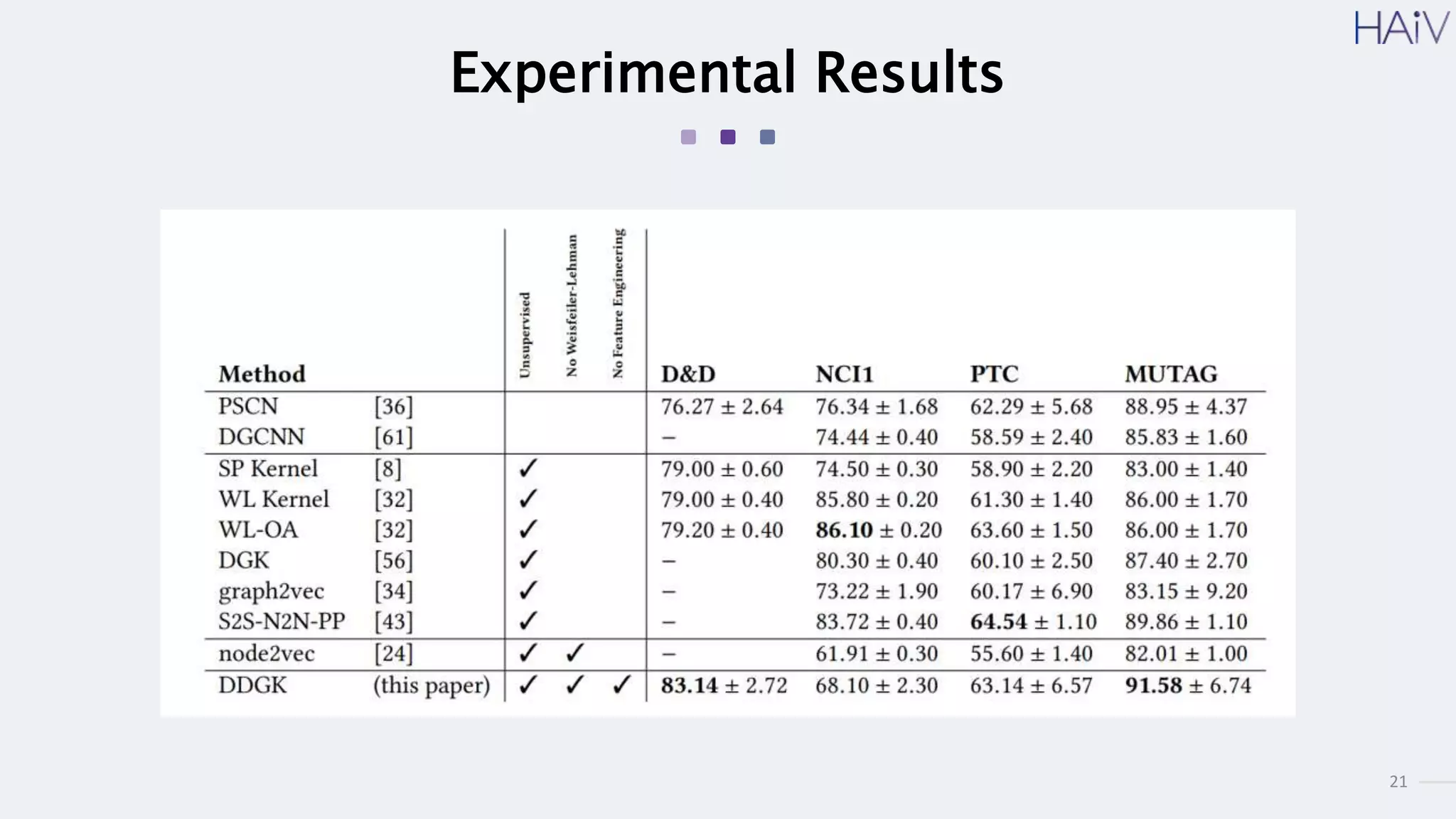
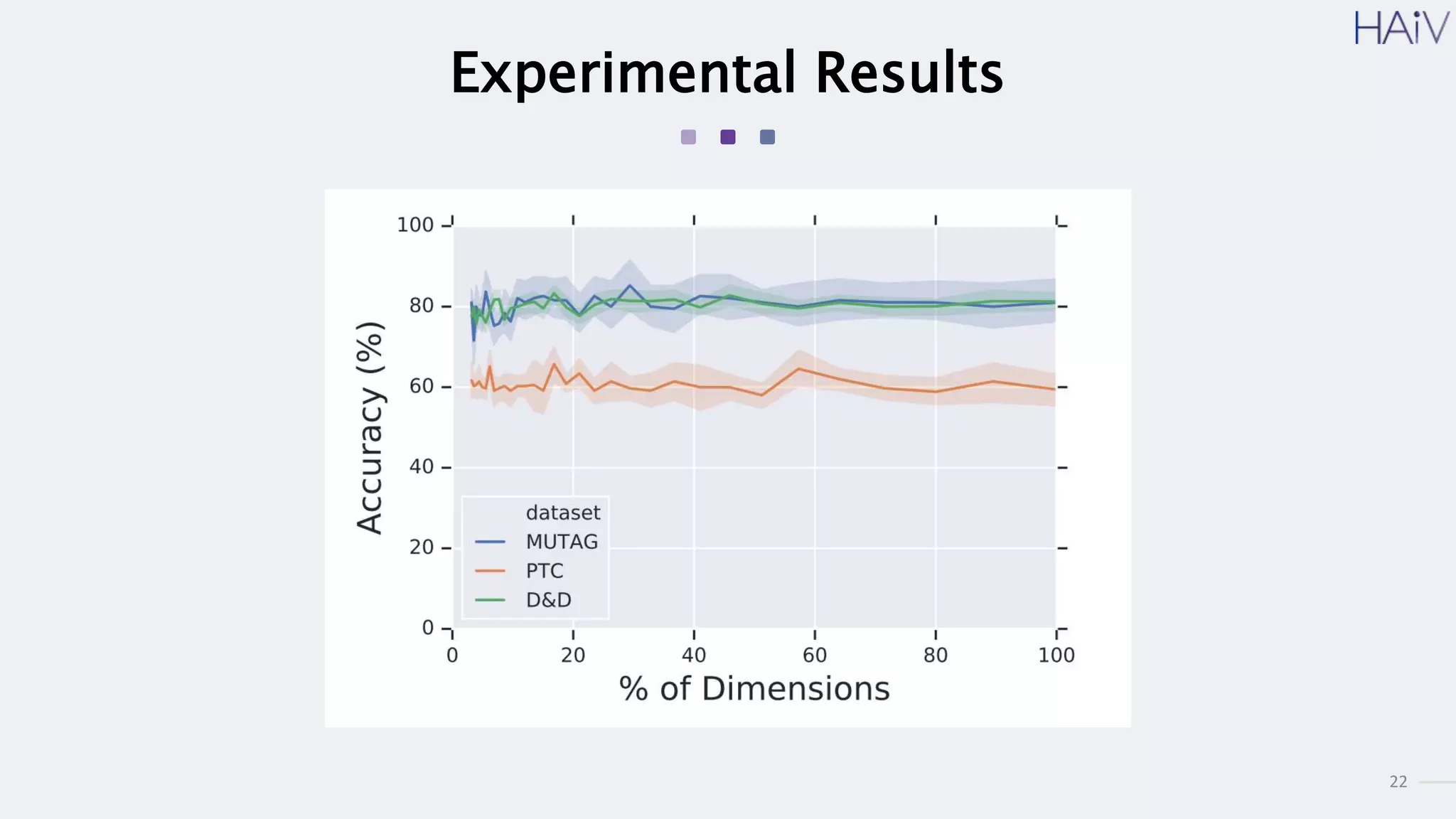
This document summarizes a research paper on learning graph representations for deep divergence graph kernels (DDGK). DDGK learns graph representations without supervision or domain knowledge by using a node-to-edges encoder and isomorphism attention. The isomorphism attention provides a bidirectional mapping between nodes in two graphs. DDGK then calculates a divergence score between the source and target graphs as a measure of their (dis)similarity. Experimental results showed DDGK produces representations competitive with other graph kernel baselines. The paper proposes several extensions, including different graph encoders and attention mechanisms, as well as improved regularization and scalability.

1. 2023.03.21
DDGK: Learning Graph Representations for Deep
Divergence Graph Kernels
Rami Al-Rfou, Dustin Zelle, and Bryan Perozzi
WWW ‘19
Nguyen Minh Duc

2. Contents
• Introduction
• Related Works
• Model Description
• DDGK Algorithm
• Experimental Results
• Extensions and Future Works
• Conclusion

3. 3
Introduction
- Graph representation learning usually relies on
- Supervised learning
- Feature engineering
- Generic representations of graphs
- Algorithmic approach
- Graph similarity measure is hard due to
- NP-hard
- Graph isomorphism
- DDGK learns without supervision and domain knowledge

4. 4
Contributions
Deep Divergence Graph Kernels (DDGK)
Isomorphism Attention
Experimental Results

5. 5
Related Works
Traditional Graph Kernels:
- Graph Edit Distance (Gao, et al., 2010) and Maximum Common Subgraph (Bunke, et al., 2002)
- Weisfeiler-Lehman Graph Kernels (Kriege, et al., 2016)
Node Embedding Methods:
- DeepWalk (Perozzi, et al., 2014)
- Graph Attention (Abu-El-Haija, et al., 2018)
Graph Statistics (Feature engineering):
- NetSmilie (Berlingerio, et al., 2012)
- DeltaCon (Koutra, et al., 2013)
Supervised Graph Similarity
- CNN for graphs (Niepert, et al., 2016)
- Graph Convolutional Networks (T. Kipf and M. Welling, 2016)

6. 6
Model Description
Node-To-Edges Encoder
Input: A one-hot encoded vertex
Output: The vertex’s neighbor
Consists of Fully connected DNN
Modeled as a Multi-Label Classifier
Graph encoding
1

7. 7
Model Description
Isomorphism Attention
Given two graphs 𝑆 (Source graph) and 𝑇 (Target graph)
Provides a bidirectional mapping across the pair’s nodes
Input: A one-hot encoded vertex from 𝑇
Output: The vertex’s neighbor
Cross-Graph
Attention
2

8. 8
Model Description
Cross-Graph
Attention
2
The first attention network (𝑀𝑇→𝑆 )
Place photo here
Assigns every node in 𝑇 with a probability
distribution over the nodes of 𝑆
Consists of one Linear layer
Modeled as a multiclass classifier
𝑃𝑟 𝑣𝑗 𝑢𝑖 =
𝑒𝑀𝑇→𝑆(𝑣𝑗,𝑢𝑖)
𝑣𝑘∈𝑉𝑆
𝑒𝑀𝑇→𝑆(𝑣𝑘,𝑢𝑖)

9. 9
Model Description
Cross-Graph
Attention
2
The reverse attention network (𝑀𝑆→𝑇 )
Place photo here
Maps the neighborhood in 𝑆 to the neighborhood in 𝑇
Consists of one Linear layer
Modeled as a multilabel classifier
𝑃𝑟 𝑢𝑗 𝑁(𝑣𝑖) =
1
1 + 𝑒−𝑀𝑆→𝑇(𝑢𝑗,𝑁 𝑣𝑖 )

10. 10
Model Description
Cross-Graph
Attention
2
Isomorphism Attention
Place photo here

11. 11
Model Description
Node attribute regularizer
Attributes
Consistency
3
Attribute distribution over nodes
Vertices and edges could have their own
attributes
Cross-Graph attention could provide several
equally good mapping
Solution: adding regularizing losses to
preserve nodes and edges attributes
Replace 𝑄𝑛 with 𝑄𝑒, we obtain Edge Attribute
Regularizer

12. 12
DDGK Algorithm
Parameter specification
The Algorithm
1

13. 13
DDGK Algorithm
Train source graph encodings
The Algorithm
1

14. 14
DDGK Algorithm
Train the Cross-Graph Attention
The Algorithm
1

15. 15
DDGK Algorithm
Save the similarity score in the matrix 𝚿
for every pair of source and target graph
The Algorithm
1
Could be used as a representation vector

16. 16
DDGK Algorithm
- Since Ψ is not a perfect function, 𝐷(𝑆| 𝑆 ≠ 0 could
happen.
- Setting
𝐷(𝑆| 𝑇 ≔ 𝐷(𝑆| 𝑇 − 𝐷(𝑆||𝑆)
ensures 𝐷(𝑆| 𝑆 = 0
- If symmetry is required, we can define
𝐷(𝑆| 𝑇 ≔ 𝐷(𝑆| 𝑇 + 𝐷(𝑇||𝑆)
Graph
Divergence
2

17. 17
DDGK Algorithm
DDGK requires 𝑂(𝑇𝑁2
𝑉) computations, where
𝑇 = max(𝜌, 𝜏)
𝑁 = The number of graphs
𝑉 = The average number of nodes
Linear layers in Cross-Graph Attention could be replaced
by a DNN with fixed size hidden layers to reduce the
network size from 𝑂( 𝑉𝑆 × 𝑉𝑇 ) to 𝑂( 𝑉𝑆 + 𝑉𝑇 )
Scalability
3
For large number of source graphs, we could sample 20%
of them and DDGK could still achieve high accuracy

18. 18
Experimental Results

19. 19
Experimental Results

20. 20
Experimental Results

21. 21
Experimental Results

22. 22
Experimental Results

23. 23
Experimental Results

24. 24
Extensions & Future Works
Graph Encoders
- Edge-to-Nodes Encoder.
- Neighborhood Encoder.
Attention Mechanism
- Subgraph alignment.
Regularization
- Better regularization to avoid overfitting.
Feature Engineering
- Combination of the two could be useful for graph classification.
Scalability
- Perozzi’s newer work: “Just SLaQ When You Approximate: Accurate Spectral Distances for Web-Scale
Graphs, WWW ’20” could handle graphs with billions of nodes within an hour.

25. 25
Conclusion
- Neural Networks can learn powerful representations of graphs without feature engineering.
- Proposed DDGK:
- Graph Encoder
- Isomorphism preserving attention
- Provide interpretability into the alignment of pairs of graph
- Divergence score to measure (dis)similarity between source and target graphs
- Representations produced by DDGK are competitive with challenging baselines.

26. Thank you
Q&A time!

27. 27
Icon Pack
https://www.flaticon.com

28. 28
Design Pack
Adjust size!
Image caption here
Place photo here
Text here
Photo here
Photo title
Description
T
T
T
T