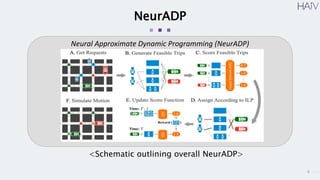
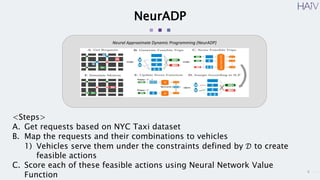
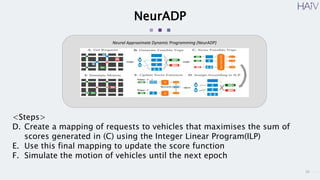
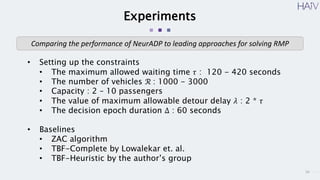
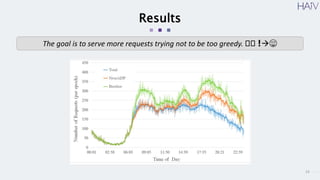
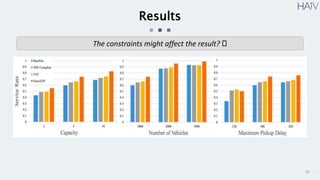
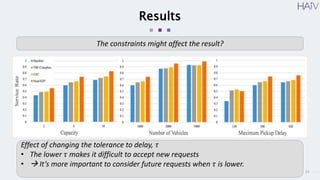
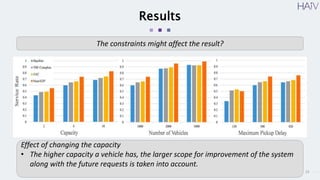
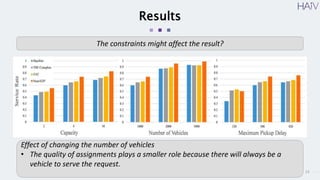
This document summarizes a research paper on using neural approximate dynamic programming (NeurADP) to solve the ride-pooling matching problem (RMP) of optimally assigning passenger requests to vehicles. The key contributions are developing NeurADP, which uses a neural network to approximate the value function within an ADP framework, and connecting it to reinforcement learning. This allows NeurADP to handle the complex RMP involving partially filled vehicles better than prior methods. The researchers test NeurADP on New York City taxi data and find that changing constraints like maximum wait time and vehicle capacity affects NeurADP's ability to serve more requests while avoiding myopic assignments.

1. 2022.03.18
Neural Approximate Dynamic Programming for
On-Demand Ride-Pooling
Sanket Shah, Meghna Lowalekar, Pradeep Varakantham
AAAI ’19
Hongkyu Lim

2. Contents
• Introduction
• Background
• Ride-pool Matching
Problem(RMP)
• NeurADP: Neural Approximate
Dynamic Programming
• Experiment
• Results

3. 3
Introduction
• On-Demand Ride- Pooling Unlike Taxi-on-Demand (ToD)
• Benefits
a) Reducing costs
b) Making more money per trip
c) Covering more # of passengers with the same or less # of cars
• Ride-Pool Matching Problem(RMP)
• Markov Decision Process
• Approximate Dynamic Programming(ADP)
• Integer Linear Program(ILP)
• Deep Reinforcement Learning (Use of Neural Network in approximating
value function by connecting it to Reinforcement Learning)

4. 4
Introduction
1) Relying on the traditional planning approaches to model the RMP
• It does not scale to on-demand city-scale scenarios.
2) Greedy search mechanism
• It does not consider the impact of a given assignment on future assignments.
3) Reinforcement Learning to address myopic assignments
• It cannot be extended to deal with the task when vehicles get more than one
passenger at a time.
4) Approximate Dynamic Programming framework to solve the ToD problem
• Linear Program does not hold for the RMP with arbitrary vehicle capacities.
• Current ADP does not consider cases in which vehicles are already partially filled
with prior passengers.
The constraints the researchers ran into in the past 😫

5. 5
Introduction
1) Arbitrary capacity RMP problem as an ADP
2) Proposign Neural ADP(NeurADP)
• A general ADP method that can learn value functions.
(approximated using Neural Networks) from ILP based assignment
problems.
3) Bring techniques from Deep Q-Networks to improve the stability and
scalability of NeurADP
Contributions 🥴

6. 6
Background
1) A framework based on Markov Decision Process(MDP) model
 ADP tackles large multi-period stochastic fleet optimization
problems.
Approximate Dynamic Programming(ADP)
• MDP :
• ADP :

7. 7
Ride-pool Matching Problem (RMP)
1) Passenger Fleet matching algorithm
 Consider a fleet of vehicles with Random initial locations.
How to serve requests with the provided number of vehicles?
• 𝒢 ∶ Road Network. (ℒ, ℰ) (set of street intersections ,adjacency of
intersections)
• 𝒰 ∶ Combination of requests
• ℛ ∶ Vehicles or resources
• 𝒟 ∶ Set of constraints on delay  {𝜏, 𝜆}
• Δ ∶ Decision epoch duration
• 𝒪 : Objective  Number of Car-pooling cases

8. 8
NeurADP
<Schematic outlining overall NeurADP>
Neural Approximate Dynamic Programming (NeurADP)

9. 9
NeurADP
<Steps>
A. Get requests based on NYC Taxi dataset
B. Map the requests and their combinations to vehicles
1) Vehicles serve them under the constraints defined by 𝒟 to create
feasible actions
C. Score each of these feasible actions using Neural Network Value
Function
Neural Approximate Dynamic Programming (NeurADP)

10. 10
NeurADP
<Steps>
D. Create a mapping of requests to vehicles that maximises the sum of
scores generated in (C) using the Integer Linear Program(ILP)
E. Use this final mapping to update the score function
F. Simulate the motion of vehicles until the next epoch
Neural Approximate Dynamic Programming (NeurADP)

11. 11
NeurADP
• 1 to 1 mapping for ToD is a simple task operated in Linear
Programming.
• However, many to 1 mapping is hard.
• 2 cases
• Single empty vehicle
• Partially filled vehicle
• The task needs to be solved with respect to unexpected
occurrences.
• It cannot be solved with Linear Programming.
Approximate Dynamic Programming(ADP)

12. 12
NeurADP
• Past work in ADP for ToD uses the dual values to update the
parameters of their value function approximation.
• The best action in optimizing RMP is to apply Integer Linear
Program(ILP)
• ILP has bad LP-relaxations
• We cannot use LP-dual to update our value function.
• Consequently, we connect ADP to Reinforcement Learning.
• Use the more general Bellman update to optimize the value
function.
No more LP-duals

13. 13
NeurADP
• Past work in ADP addresses high dimensionality by hand-crafted
attributes(ex. Aggregated number of vehicles in each location.)
• It’s okay… for ToD because it is one-to-one mapping.
• However, how about RMP?
• Each vehicle has different number of passengers going to
multiple different locations…
• Use Neural Network based value function to automatically learn a
compact low dimensional representation of the large state space.
Curse of Dimensionality 😵💫

14. 14
NeurADP
• Naïve approaches to approximating Neural Network value functions in
Deep Reinforcement Learning is unstable.
• Replace LP-duals with more general Bellman update for stepping up
the Neural Network value function
• It’s named “Neural ADP”.
🥴 Challenges of learning a Neural Network value function

15. 15
NeurADP
• 2 Steps for constraints
1. Constraints at the vehicle level
 Satisfying delay constraints 𝒟 and vehicle capacity constraints
2. Constraints at the system level
 Each request is assigned to at most one vehicle.
How to handle exponential action space?

16. 16
Experiments
• Setting up the constraints
• The maximum allowed waiting time 𝜏 : 120 - 420 seconds
• The number of vehicles ℛ : 1000 - 3000
• Capacity : 2 – 10 passengers
• The value of maximum allowable detour delay 𝜆 : 2 * 𝜏
• The decision epoch duration Δ : 60 seconds
• Baselines
• ZAC algorithm
• TBF-Complete by Lowalekar et. al.
• TBF-Heuristic by the author’s group
Comparing the performance of NeurADP to leading approaches for solving RMP

17. 17
Experiments
• Dataset
• New York Yellow Taxi Dataset 2016
• Road network : osmnx with ‘drive’ network type
• In total, 4373 nodes & 9540 edges
• Manhattan only
• Pickup time is converted to approximate decision epoch based on
Δ.
• On average, 322,714 requests in a day
• 19820 requests during peak hour
Comparing the performance of NeurADP to leading approaches for solving RMP

18. 18
Results
• Dataset
• New York Yellow Taxi Dataset 2016
• Road network : osmnx with ‘drive’ network type
• In total, 4373 nodes & 9540 edges
• Manhattan only
• Pickup time is converted to approximate decision epoch based on
Δ.
• On average, 322,714 requests in a day
• 19820 requests during peak hour
The goal is to serve more requests trying not to be too greedy. 🥴

19. 19
Results
The goal is to serve more requests trying not to be too greedy. 🥴🥴 ❗️😵

20. 20
Results
The constraints might affect the result? 🥴

21. 21
Results
The constraints might affect the result?
Effect of changing the tolerance to delay, 𝜏
• The lower 𝜏 makes it difficult to accept new requests
•  It’s more important to consider future requests when 𝜏 is lower.

22. 22
Results
The constraints might affect the result?
Effect of changing the capacity
• The higher capacity a vehicle has, the larger scope for improvement of the system
along with the future requests is taken into account.

23. 23
Results
The constraints might affect the result?
Effect of changing the number of vehicles
• The quality of assignments plays a smaller role because there will always be a
vehicle to serve the request.

24. Thank you