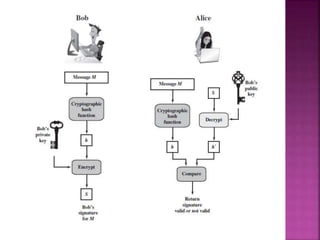
1. Digital signatures provide authentication of digital documents by using asymmetric cryptography techniques. A digital signature is generated using a private key and can be verified by anyone using the corresponding public key. 2. There are various types of attacks against digital signature schemes like key-only attacks, generic chosen message attacks, and adaptive chosen message attacks. The security goals are to prevent total key breaks or the ability to forge signatures selectively or existentially. 3. A secure digital signature scheme must produce signatures that depend on the message, use secret information to prevent forgery and denial, be efficient to generate and verify, and make forgery computationally infeasible. Timestamps can be included to require message freshness.

1. HASH FUNCTIONS & DIGITAL
SIGNATURES
V.Thamizharasan
Assistant professor
Department of ECE
Erode Sengunthar Engineering College

2. 1. Disclosure:
Release of message contents to any person.
2. Traffic analysis:
How to communicate(prototype),
Frequency and duration of connections,
the number and length of messages.
3. Masquerade:
Insertion of messages into the network from a
fraudulent source.
creation of messages by an opponent.
Fraudulent acknowledgments.
4. Content of message modification
5. Sequence of message modification:

3. 6.Timing modification:
Delay or replay of messages
7. Source repudiation.
Denial of transmission of message by
source.
8. Destination repudiation:
Denial of receipt of message by destination.

4.  Two levels of functionality:
1. A value to be used to authenticate a message.
2. Receiver to verify the authenticity of a message.
Types of functions:
 Hash function:A function that maps a message of
any length into a fixed length hash value, which
serves as the authenticator
 Message encryption: The cipher text of the entire
message serves as its authenticator
 Message authentication code (MAC):
A function of the message and a secret key that
produces a fixed-length value that serves as the
authenticator

9. Message encryption

11. Message Authentication Code

13.  Brute-Force Attacks:
 To attack a hash code Given a fixed message x with
n-bit hash code h = H(x),
a brute-force method of finding a collision is to pick a
random bit string y and check if H(y) = H(x).
 The attacker can do this repeatedly off line
 desired security property Computation resistance
Given one or more text-MAC pairs [xi, MAC(K, xi)], it is
computationally infeasible to compute any text-MAC
pair [x, MAC(K, x)] for any new input x ≠ xi.
 the attacker would like to come up with the valid MAC
code for a given message x.
 There are two lines of attack possible:
 attack the key space and attack the MAC value.

14. 1. If an attacker can determine the MAC key
To generate a valid MAC value for any input x.
Then the attacker can compute the n-bit tag on the known
text for all possible keys.
one operation for each of the 2^k possible key values.
if more than one key is found to produce the correct
value, additional text-tag pairs must be tested.
2. An attacker can also work on the tag
without attempting to recover the key.
 The level of effort for brute-force attack on a MAC
algorithm can be expressed as min(2^k, 2^n).

15.  Cryptanalysis:
 cryptanalytic attacks on MAC algorithms seek to
exploit some property of the algorithm to
perform some attack other than an exhaustive
search.
 There is much more variety in the structure of
MACs than in hash functions, so it is difficult to
generalize about the cryptanalysis of MACs

16.  SHA was developed by the National Institute
of Standards and Technology (NIST)1993
 These new versions have the same underlying
structure and use the same types of modular
arithmetic and logical binary operations as
SHA-1.

17.  Input a message with a maximum length of less than 2^128
bits.
 Produces as output a 512-bit message digest.

18.  1. Append padding bits:
The message is padded so that its length is congruent to 896
modulo 1024 [length = 896(mod 1024)].
the number of padding bits is in the range of 1 to 1024.
The padding consists of a single 1 bit followed by the necessary
number of 0 bits.
 2. Append length:
A block of 128 bits is appended to the message.
 3.Initialize hash buffer.
 A 512-bit buffer is used to hold intermediate and final results of the
hash function.
 The buffer can be represented as eight 64-bit registers (a, b, c, d,
e, f, g, h).

19. These values are stored in big-endian format:
which is the most significant byte of a word in the low-address
(leftmost) byte position.
These words were obtained by taking the first sixty-four bits of the
fractional parts of the square roots of the first eight prime numbers.

20. 4. Process message in 1024-bit (128-word) blocks.

21. Module that consists of 80 rounds.
Each round t makes use of a 64-bit value Wt, derived from the
current 1024-bit block being processed (Mi).
Each round also makes use of an additive constant Kt.
These words represent the first 64 bits of the fractional parts of the
cube roots of the first 80 prime numbers.
The output of the eightieth round is added to the input to the first
round (Hi-1) to produce Hi.
using addition modulo 2^64.

23. 5 Output.
After all N 1024-bit blocks have been processed,
the output from the Nth stage is the 512-bit message digest.

25. Six of the eight words of the output of the round function involve simply
permutation (b, c, d, f , g, h) by means of rotation
Only two of the output words (a, e) are generated by substitution
Word e is a function of input variables (d, e, f , g, h), as well as the round word
Wt constant Kt.
Word a is a function of all of the input variables except d, as well as the round
word Wt and the constant Kt.

28. 1. Cryptographic hash functions such as MD5 and
SHA generally execute faster in software than
symmetric block ciphers such as DES.
2. Library code for cryptographic hash functions
is widely available.
 A hash function such as SHA was not designed for use as a MAC
and cannot be used directly for that purpose, because it does
not rely on a secret key.
 proposals for the incorporation of a secret key into an existing
hash algorithm.
HMAC has been issued as RFC 2104, has been chosen as the
mandatory-to-implement MAC for IP security, and is used in
other Internet protocols, such as SSL

29.  To use, without modifications, available hash functions.
 To allow for easy replaceability of the embedded hash
function in case faster or more secure hash functions are
found or required.
 To preserve the original performance of the hash
function without incurring a significant degradation.
 To use and handle keys in a simple way.
 To have a well understood cryptographic analysis of the
strength of the authentication mechanism based on
reasonable assumptions about the embedded hash
function.

33. where f(cv, block) is the
compression function

34.  Two Algorithm:
1. Data Authentication Algorithm (DAA)
based on DES
security weaknesses in this algorithm have
been discovered
 defined as using the cipher block chaining (CBC) mode
of operation of DES
 initialization vector of zero
 64-bit blocks: D1, D2,...., DN.
 final block is padded on the right with zeroes to form
a full 64-bit block.

35. Data Authentication Algorithm (DAA)

36.  DAA has been widely adopted in government
and industry.
 Only messages of one fixed length of mn bits
are processed, where n is the cipher block
size and m is a fixed positive integer.
 CBC MAC of a one-block message X, say T =
MAC(K, X), the adversary immediately knows
the CBC MAC for the two block message
X|| (X xor T) since this is once again T.

37.  one key K of length k to be used at each step
of the cipher block chaining and two keys of
length b.
 two n-bit keys could be derived from the
encryption key,
 Is the Cipher-based Message Authentication
Code (CMAC) mode of operation for use
with AES and triple DES.

38.  when the message is an integer multiple n of
the cipher block length b.
 AES, b = 128, and for triple DES, b = 64.
 message is divided into n blocks (M1, M2,…..,
Mn).
 k-bit encryption key K
 b-bit constant, K1.
 AES, the key size k is 128, 192, or 256 bits
 triple DES, the key size is 112 or 168 bits.

41.  most important development from the work on
public-key cryptography is the digital signature.

43.  Mary may forge a different message and claim
that it came from John. Mary would simply have
to create a message and append an
authentication code using the key that John and
Mary share.
 An electronic funds transfer takes place, and the receiver
increases the amount of funds transferred and claims that
the larger amount had arrived from the sender
 John can deny sending the message. Because it
is possible for Mary to forge a message, there is
no way to prove that John did in fact send the
message.
 an electronic mail message contains instructions to a stockbroker
for a transaction that subsequently turns out badly. The sender
pretends that the message was never sent.

44.  It must verify the author and the date and
time of the signature.
 It must authenticate the contents at the time
of the signature.
 It must be verifiable by third parties, to
resolve disputes.

45.  Key-only attack C only knows A’s public key.
 Known message attack C is given access to a set of
messages and their signatures.
 Generic chosen message attack
C chooses a list of messages before attempting to breaks A’s signature
scheme, independent of A’s public key. C then obtains from A valid
signatures for the chosen messages. The attack is generic, because it
does not depend on A’s public key; the same attack is used against
everyone.
 Directed chosen message attack
Similar to the generic attack, except that the list of messages to be
signed is chosen after knows A’s public key but before any signatures
are seen.
 Adaptive chosen message attack
C is allowed to use A as an “oracle.” This means that C may request from
A signatures of messages that depend on previously obtained message-
signature pairs

46.  Total break: C determines A’s private key.
 Universal forgery: C finds an efficient signing
algorithm that provides an equivalent way of constructing
signatures on arbitrary messages.
 Selective forgery: C forges a signature for a
particular message chosen by C.
 Existential forgery: C forges a signature for at least
one message. C has no control over the message.
Consequently, this forgery may only be a minor nuisance to
A.

47.  The signature must be a bit pattern that depends on
the message being signed.
 The signature must use some information unique to
the sender to prevent both forgery and denial.
 It must be relatively easy to produce the digital
signature.
 It must be relatively easy to recognize and verify the
digital signature.
 It must be computationally infeasible to forge a
digital signature, either by constructing a new
message for an existing digital signature or by
constructing a fraudulent digital signature for a given
message.
 It must be practical to retain a copy of the digital
signature in storage.

48.  Digital signature scheme that involves only
the communicating parties (source,
destination). It is assumed that the
destination knows the public key of the
source.
 Confidentiality can be provided by encrypting
the entire message plus signature with a shared
secret key (symmetric encryption).
 The validity of the scheme just described depends on the
security of the sender’s private key
 require every signed message to include a timestamp

49.  The Elgamal signature scheme involves the
use of the private key for encryption and the
public key for decryption.

52.  Its based on discrete logarithms
 Minimizes the message-dependent amount of
computation required to generate a signature.
 signature generation does not depend on the
message
 The scheme is based on using a prime modulus p,
with p - 1 having a prime factor q of appropriate
size;
 p is a 1024-bit number, and q is a 160-bit number
 which is also the length of the SHA-1 hash value.