Bloom filters are a space-efficient probabilistic data structure for representing a set in order to support membership queries. They allow for false positives but not false negatives. The document discusses how bloom filters work using hash functions to set bits in a bit vector, allowing for fast set membership checks. It also covers extensions like counting bloom filters that can support deletions by incrementing and decrementing counters, and variations like distance-sensitive bloom filters and bloomier filters.

1. Bloom Filters
Kira Radinsky
Slides based on material from:
Michael Mitzenmacher and Hanoch Levy

2. Motivation - Cache
• Lookup questions:
Does item “x” exist in a set?
• Data set may be very big or expensive to
access. Filter lookup questions with negative
results before accessing data.
• Allow false positive errors, as they only cost us an
extra data access.
• Don’t allow false negative errors, because they
result in wrong answers.

3. Application of Bloom Filters:
Distributed Web Caches
Web Cache 1 Web Cache 2 Web Cache 3
Web Cache 6Web Cache 5Web Cache 4
• Send Bloom filters of URLs.
• False positives do not hurt much.
– Get errors from cache changes anyway

4. Web Caching
• Summary Cache: [Fan, Cao, Almeida, & Broder]
If local caches know each other’s content...
…try local cache before going out to Web
• Sending/updating lists of URLs too expensive.
• Solution: use Bloom filters.
• False positives
– Local requests go unfulfilled.
– Small cost, big potential gain

5. The Problem Solved by BF:
Approximate Set Membership
• Lookup Problem: Given a set S = {x1,x2,…,xn}, construct
data structure to answer queries of the form
“Is y in S?”
• Data structure should be:
– Fast (Faster than searching through S).
– Small (Smaller than explicit representation).
• To obtain speed and size improvements, allow some
probability of error.
– False positives: y  S but we report y  S
– False negatives: y  S but we report y  S

6. Bloom Filters
Start with an m bit array, filled with 0s.
Hash each item xj in S k times. If Hi(xj) = a, set B[a] = 1.
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0B
0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 0B
To check if y is in S, check B at Hi(y). All k values must be 1.
0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 0B
0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 0B
Possible to have a false positive; all k values are 1, but y is not in S.

7. Bloom Filter
01000 10100 00010
x
h1(x) h2(x) hk(x)
V0 Vm-1
h3(x)

8. Advantages
• No Overflow
• Union and intersection of Bloom filters
– A simple bitwise OR and AND operations
• Applications:
– Google BigTable
– The Squid Web Proxy Cache uses Bloom filters for
cache digests.

9. Bloom Errors
01000 10100 00010
h1(x) h2(x) hk(x)
V0 Vm-1
h3(x)
a b c d
x didn’t appear, yet its bits are already set

10. Example
0
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0 1 2 3 4 5 6 7 8 9 10
Hash functions
Falsepositiverate
m/n = 8
Opt k = 8 ln 2 = 5.45...

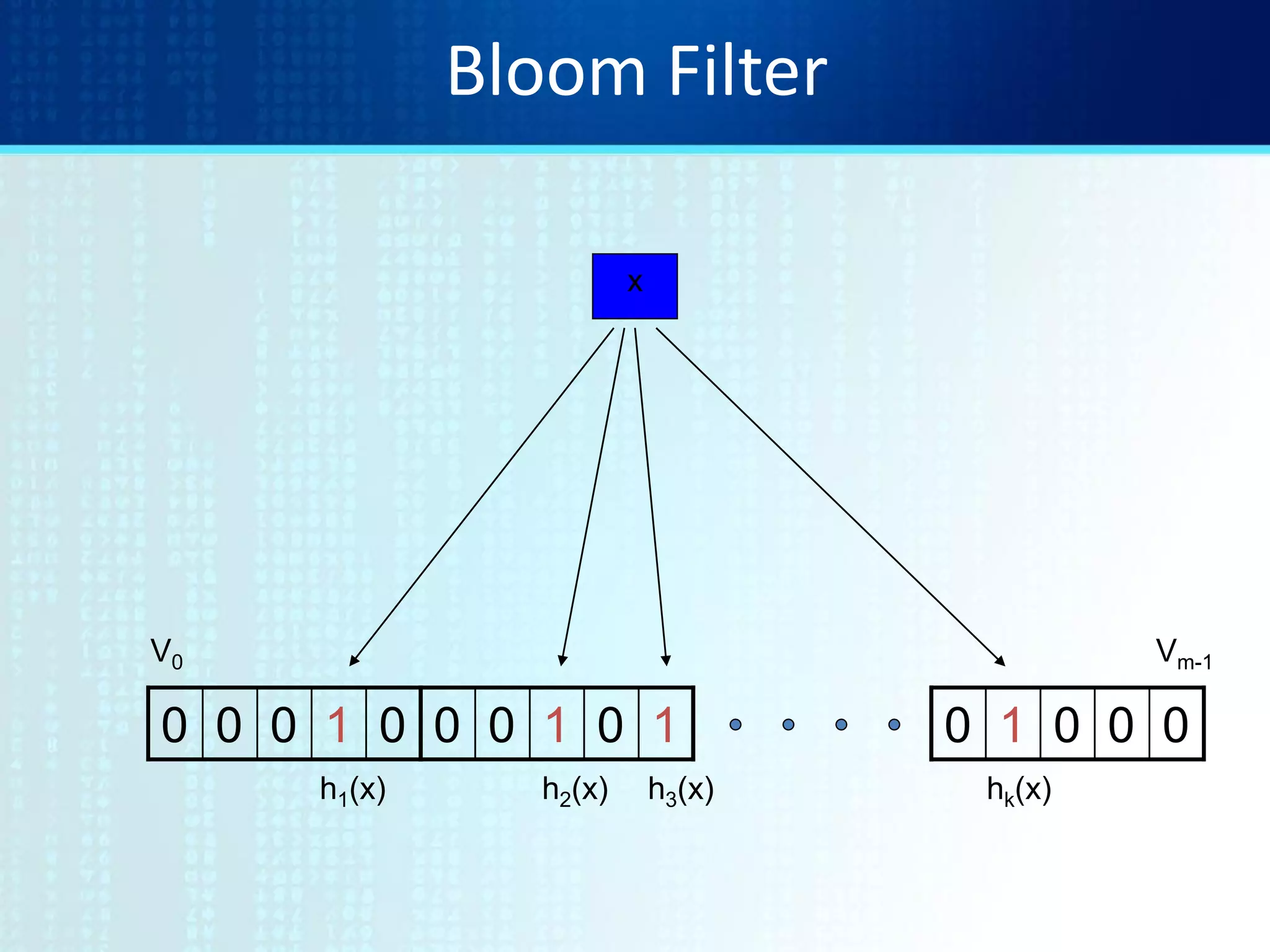
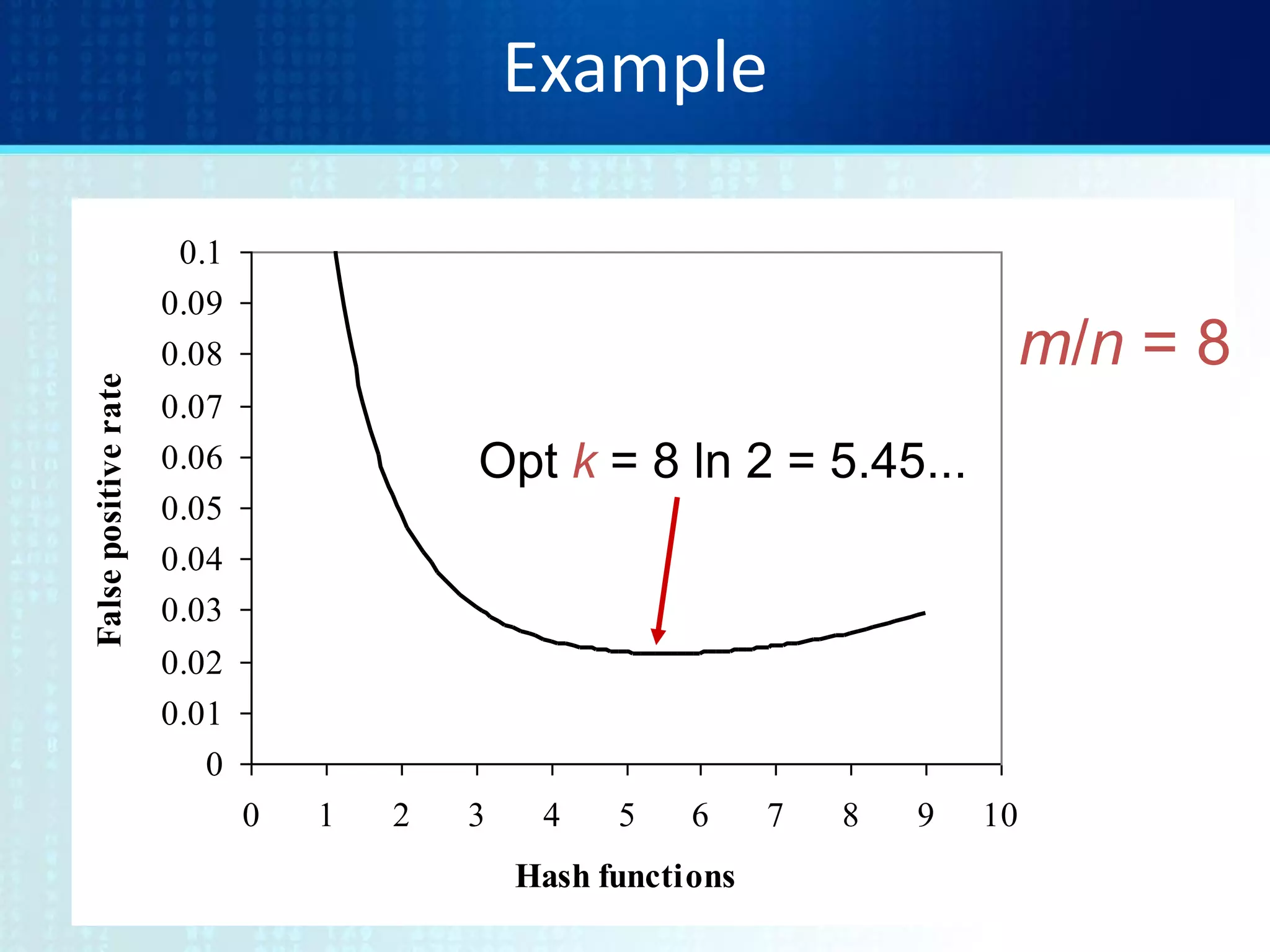
11. Tradeoffs
• Three parameters.
– Size m/n : bits per item.
• |U| = n: Number of elements to encode.
• hi: U[1..m] : Maintain a Bit Vector V of size m
– Time k : number of hash functions.
• Use k hash functions (h1..hk)
– Error f : false positive probability.

12. Bloom Filter Tradeoffs
• Three factors: m,k and n.
• Normally, n and m are given, and we select k.
• Small k
– Less computations.
– Actual number of bits accessed (nk) is smaller, so the chance of a “step
over” is smaller too.
– However, less bits need to be stepped over to generate an error.
• For big k, the exact opposite holds.
• Not surprisingly, when k is optimal, the “hit ratio” (ratio of bits
flipped in the array) is exactly 0.5

13. Alternative Approach for
Bloom Filters: Perfect Hashing Approach
Element 1 Element 2 Element 3 Element 4 Element 5
Fingerprint(4) Fingerprint(5) Fingerprint(2) Fingerprint(1) Fingerprint(3)

14. Perfect Hashing Approach
• Folklore Bloom filter construction.
– Recall: Given a set S = {x1,x2,x3,…xn} on a universe U, we want
to answer membership queries.
– Method: Find an n-cell perfect hash function for S.
• Maps set of n elements to n cells in a 1-1 manner.
– Then keep bit fingerprint of item in each cell.
Lookups have false positive < e.
– Advantage: each bit/item reduces false positives by a factor
of 1/2, vs ln 2 for a standard Bloom filter.
• Negatives:
– Perfect hash functions non-trivial to find.
– Cannot handle on-line insertions.
 )/1(log2 e

15. Bloom Filters and Deletions
• Cache contents change
– Items both inserted and deleted.
• Insertions are easy – add bits to BF
• Can Bloom filters handle deletions?
– Use Counting Bloom Filters to track
insertions/deletions at hosts;
– Send Bloom filters.

16. Handling Deletions
• Bloom filters can handle insertions, but not
deletions.
• If deleting xi means resetting 1s to 0s, then
deleting xi will “delete” xj.
0 1 0 0 1 0 1 0 0 1 1 1 0 1 1 0B
xi xj

17. Counting Bloom Filters
Start with an m bit array, filled with 0s.
Hash each item xj in S k times. If Hi(xj) = a, add 1 to B[a].
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0B
0 3 0 0 1 0 2 0 0 3 2 1 0 2 1 0B
To delete xj decrement the corresponding counters.
0 2 0 0 0 0 2 0 0 3 2 1 0 1 1 0B
Can obtain a corresponding Bloom filter by reducing to 0/1.
0 1 0 0 0 0 1 0 0 1 1 1 0 1 1 0B

18. Counting Bloom Filters: Overflow
• Must choose counters large enough to avoid
overflow.
• Poisson approximation suggests 4 bits/counter.
– Average load using k = (ln 2)m/n counters is ln 2.
– Probability a counter has load at least 16:
• Failsafes possible.
17E78.6!16/)2(ln 162ln
 
e

19. Variations and Extensions
• Distance-Sensitive Bloom Filters
• Bloomier Filter

20. Extension: Distance-Sensitive Bloom Filters
• Instead of answering questions of the form
we would like to answer questions of the form
• That is, is the query close to some element of the set, under
some metric and some notion of close.
• Applications:
– DNA matching
– Virus/worm matching
– Databases
• Some initial results [KirschMitzenmacher]. Hard.
.SyIs 
.SxyIs 

21. Extension: Bloomier Filter
• Bloom filters handle set membership.
• Counters to handle multi-set/count tracking.
• Bloomier filter [Chazelle, Kilian, Rubinfeld, Tal]:
– Extend to handle approximate functions.
– Each element of set has associated function value.
– Non-set elements should return null.
– Want to always return correct function value for set
elements.
– A false positive returns a function value for a non-null
element.