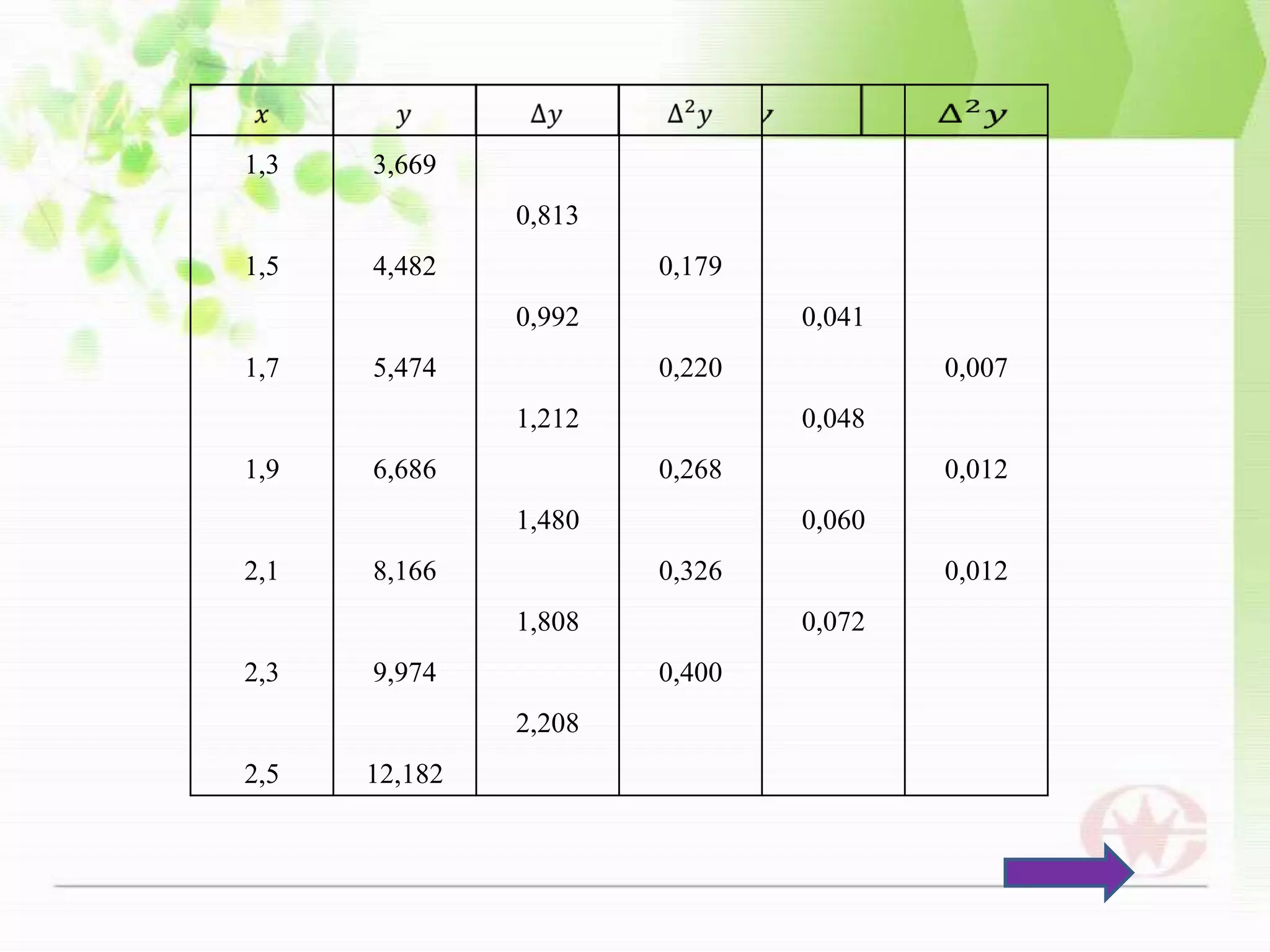
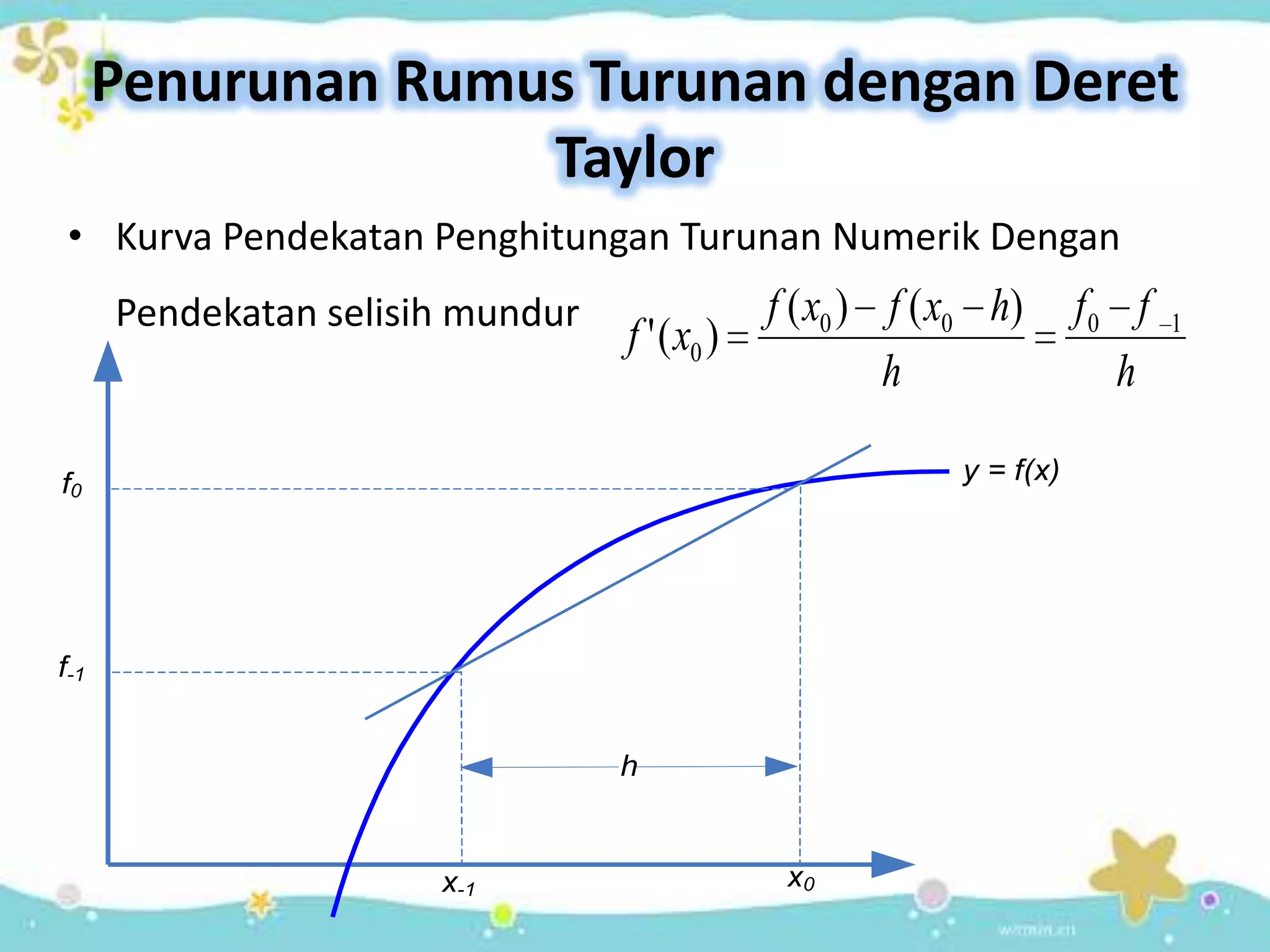
Dokumen ini membahas turunan numerik menggunakan metode Newton-Gregory Backward (NGB) untuk menghitung derivatif suatu fungsi yang dinyatakan dalam data titik atau ketika fungsi terlalu rumit untuk diferensiasi analitik. Metode ini menerapkan polinom interpolasi dan deret Taylor untuk menghitung turunan pertama dan kedua dengan menggunakan pendekatan selisih mundur. Contoh perhitungan dan galat juga disajikan untuk menunjukkan penerapan metode ini.