This document discusses turbo codes, which are a type of error correction code built by parallel concatenating two convolutional code blocks. It focuses on investigating the iterative decoding of turbo codes. The bit error rate is calculated over multiple iterations of decoding and plotted against signal to noise ratio. Quadratic permutation polynomial and random interleavers are analyzed. Results show turbo codes with a memory of 3 and 1280 bit interleaver achieve the best performance, reaching a bit error rate of 10-5 at -1.2 dB after 10 iterations of decoding.

1. From Convolutional Codes to Turbo Codes
Anjali Suresh Babu and Marcel Adrian Ambroze
School of Computing and Mathematics, Plymouth University
Plymouth, United Kingdom
anjali.sureshbabu@postgrad.plymouth.ac.uk
mambroze@plymouth.ac.uk
Abstract
The turbo code is the name of a class of convolutional codes which developed by parallel
concatenating two convolutional code blocks which are identical. This new class of channel
error control code is well known for its high performance at low to moderate signal to noise
ratio (SNR). This paper is about the investigative study of this high performance of the turbo
codes. The milestone about this research is the study on the iterative decoding of turbo codes.
The bit error rate (BER) is calculated during a number of the iterations and plotted against the
signal to noise ratio (SNR). This paper also explains a way of computing the so called
extrinsic and intrinsic information which were the confusing piece of work about the iterative
decoder. The turbo code performance was also analyzed in terms of the interleaver design. The
research used two types of interleavers Quadratic Permutation Polynomial (QPP) that of LTE
standard and the traditional random interleaver.
Keywords
Turbo Codes, Iterative Decoding, Bit Error rate (BER), Signal to Noise Ratio (SNR),
Quadratic Permutation Polynomial (QPP), Log likelihood Ratio (LLR), Wireless,
and Satellite.
1. Introduction
The turbo codes are the parallel concatenated form of a convolutional code. That is
the turbo codes are built by concatenating two convolutional code blocks. The
convolutional code that usually serve to design turbo codes are recursive and
systematic. By recursive it means that one of the outputs is fed back to the input or in
other words there exists a feedback path. Also all recursive convolutional codes are
non catastrophic makes it preferable for the design (Lin, 2004). This research is an
investigative study about the efficiency of an iterative decoder of turbo codes. The
section II is an overview about the turbo codes. The section III explains the turbo
decoding, the computation of extrinsic information and the interleaver design. The
section IV is about the results obtained and the analysis of the results. At last the
discussion and conclusion also mentioning the possibility of future work.

2. 2. An Overview of Turbo Codes
Consider a recursive convolutional encoder with constrain length K=4, i.e. memory
m=3 and with generators g1=17 and g2=11 in octal. The encoder block is as shown in
the figure 1. Here the RSC encoder considered is of rate r=1/2. Since the encoder is
systematic, one of the bits in the output code vector is the input bit itself. The other
bit is the parity which is generated by the using the generator g2=11.
If uk is the input bit at an instant of time k and the output code vector is Xk ={ xk
0
xk
1
} ,
(Berrou, Glavieux & Thitimajshima, 1993) for the case of encoder with rate ½. The
general form producing the output bits is as given below (Berrou, Glavieux &
Thitimajshima, 1993)
xk
1
=∑ukg1
i
mod 2 k=0,1..N-1 and i=0,1,..2m-1
xk
0
= uk
xk
0
xk
1
The turbo code is designed by concatenating two identical encoders using an
interleaver and the overall rate becomes 1/3. That is the code vector consists of
systematic bit and two parity bits. The interleaver re order the information sequence
into f(i) if i, is the bit position in the original sequence. Similar to the encoder the
turbo code decoder also have a concatenated structure. The two decoder blocks are
concatenated parallel using the interleaver that used at the encoder side. The received
vector consists of three values rk
0
, rk
1
, rk
2
corresponding to the transmitted systematic
bit, the first parity and the second parity respectively. The channel noise is additive
white Gaussian which produces random errors. The rk
0
, rk
1
are fed into the first
decoder block and the rk
0
, rk
2
into the second decoder. While rk
0
is passed through an
interleaver which produces r’k
0
which is the rearranged received values of the
information sequence.
uk
m0 m1 m2
Figure 1 RSC encoder rate ½ m=3

3. 3. Iterative Decoding
The decoder of Turbo codes are often called as iterative decoder due to its iterative
operation. The final decision about the information sequence is made after a number
of decoding iterations. The algorithm used to implement the decoder block here is
the Maximum a posterior (MAP) also called BCJR algorithm proposed by (Bahl et
al., 1974)
The MAP algorithm implemented here is a bit level trellis based (Bahl et al., 1974)
which involves the three steps associated with the corresponding trellis of the
encoder used. The three steps are as follows.
1. Calculate the branch matrix δ (i) where i={0,1}.
2. Perform the forward iteration calculating the alpha values which are the node
matrix in forward direction αj
k
j= {0, 1...., 2m-1
} and k=0,1..N-1.
3. Perform the backward iteration calculating the beta values which are the node
matrix in backward direction βj
k
j= {0, 1..., 2m-1
} and k= 0,1..N-1.
Encoder1
Encoder2I
u xk
0
xk
1
Encoded vector
Figure 2. Turbo encoder structure
Decoder1
Decoder2I DI
I
rk
1
rk
0
rk
2
Figure 3. Turbo Decoder Structure

4. If s is the present state at a trellis level, then the two next states possible are s0
’
and s1
’
corresponding to a 0 and 1 transition. The final decision is made from the LLR
calculated as below.(Lin, 2004)
LLR= log[(∑αkβk+1δk(1))/(∑ αkβk+1δk(0))].
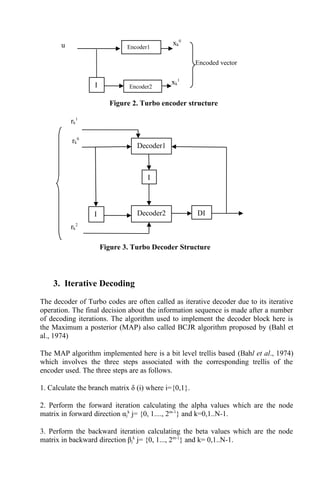
Fig 4. Iterative Turbo Decoder
The message bit is decoded as a 0 if LLR ≤ 0 and a 1 if LLR > 0.
3.1. Intrinsic Information
The LLR can be split into its three components as shown below.
LLR1
(uk)= Le
1
(uk)+La
1
(uk)+ Le
2
(uk)
LLR1
(uk)= log1[P(uk=1/rk)/P(uk=0/rk)] + log[P(1)/P(0)]+ log1[P(uk=1/rk)/P(uk=0/rk)]
The intrinsic information is one of those components which is the probability of kth
bit calculated from the channel information. The intrinsic information is represented
as La(uk) which is calculated from the bit probabilities P1
1
(k) and P1
0
(k) for the first
decoder block.
P1
1
(k) = exp (-(rk
0
-(+1))/2*σ2
)
P1
0
(k) = exp (-(rk
0
-(-1))/2*σ2
) where σ2
is the variance.
The intrinsic information La (uk) = log[P1
1
(k)/ P1
0
(k)]
3.2. Extrinsic Information
I DI
I
Decoded value
Extrinsic information
Extrinsic information
(Channel L value + Extrinsic
from MAP1)
Channel value for
parity bit y0
from
encoder2
Channel value for
the systematic
output
Channel value for
parity bit y1
from
encoder2
MAP1
MAP2
(Channel L value + Extrinsic
from MAP2)

5. The extrinsic information is the knowledge about the corresponding parity bits
transmitted. By passing the extrinsic information form decoder 1 to decoder 2, it
means the information about the first parity bit is passed to decoder 2 so that the
decoder 2 can compute an improved LLR in the following iterations. The extrinsic
information can be extracted by the LLR as follows,
Le
1
(uk)= LLR (k)- La
1
(uk) – Le
2
(uk)
In other sense the extrinsic information can be considered as the equation below.
Le
1
(uk)= log [ P(uk=1/rk
1
)/P(uk=0/rk
1
)]
3.2. Interleaver
The interleaver types considered in this research is the quadratic permutation
polynomial, random interleaver and row-column interleaver. The permutation
polynomials of three different lengths are used(Rosnes, 2012) of lengths 512, 1024
and 1280. The row-column interleaver used is a square matrix. The information bits
are written row by row into the matrix and read pseudo randomly(Fragouli & Wesel,
1999). The random interleaver is a random number generator in which the bit
positions to be permuted are generated randomly.
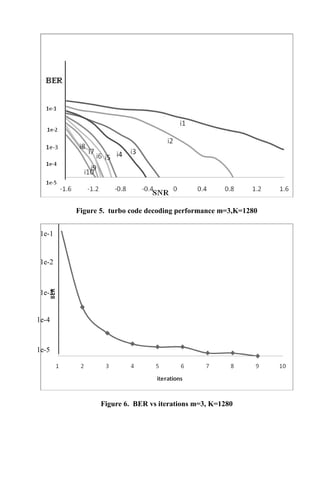
4. Results
The turbo code of rate 1/3 with memory m=3 is built using RSC encoders using
generators 17 and 11. The bit error rate (BER) is calculated at the end decoding and
plotted against the SNR. The decoding was done for a number of iterations. Using
memory m=3, in ten iterations BER 10-5
was obtained at SNR -1.2 dB. The figure 5
shows the graph plotting BER of turbo code using QPP interleaver. The BER found
to be constantly reducing in iteration. The figure 6 shows the BER constantly
reducing with increasing the number of iterations. The best BER value of range 10-5
was obtained in the ninth iteration at -0.4 dB.

6. Figure 5. turbo code decoding performance m=3,K=1280
Figure 6. BER vs iterations m=3, K=1280
1e-1
1e-2
1e-3
1e-4
1e-5

7. 5. Conclusion
In this research the iterative decoding performance of turbo codes was studied and
analyzed. The turbo code was built starting from memory m=2 up to m=4 for using
the standard generators.(Proakis, 2000) The best performance was obtained for the
case K=1280 and m=3 using generators 17 and 11. The performance was also
analysed using conventional interleavers like row-column and random interleaver.
Here the turbo code was built using the identical convolutional code blocks. Instead
of identical ones, the turbo code performance can be analysed by using different
encoder blocks with different constrain length. Also the performance can be
analyzed by varying the rate by concatenating more than two convolutional code
blocks.
6. References
Bahl, L., Cocke, J., Jelinek, F. & Raviv, J. (1974) 'Optimal decoding of linear codes for
minimizing symbol error rate (Corresp.)'. IEEE Transactions on Information Theory, 20 (2).
pp 284-287.
Berrou, C., Glavieux, A. & Thitimajshima, P. (1993) 'Near Shannon limit error-correcting
coding and decoding: Turbo-codes. 1'.[in 2, 1064-1070.
Fragouli, C. & Wesel, R. D. (1999) 'Semi- random interleaver design criteria'.[in 5, 2352-
2356.
Lin, S. (2004) Error control coding : fundamentals and applications. ed. Costello, D.J., 2nd
ed. edn. Pearson Prentice Hall, ISBN: 0-13-017973-6.
Proakis, J. G. (2000) Digital Communications. 4th ed. edn. McGraw, ISBN: 0-07-118183-0.
Rosnes, E. (2012) 'On the Minimum Distance of Turbo Codes With Quadratic Permutation
Polynomial Interleavers'. Information Theory, IEEE Transactions on, 58 (7). pp 4781-4795.