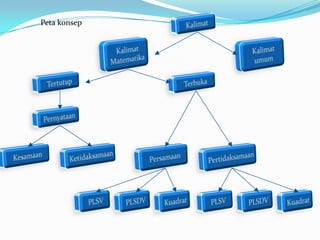
Dokumen ini membahas tentang persamaan dan pertidaksamaan linear satu variabel, termasuk definisi, cara penyelesaian, dan contoh-contoh penerapannya dalam kalimat terbuka serta ketidaksamaan. Persamaan linear ditentukan sebagai kalimat terbuka yang dihubungkan dengan tanda sama dengan, sedangkan pertidaksamaan menyatakan hubungan ketidaksamaan. Dokumen juga memberikan metode untuk mencari himpunan penyelesaian dari persamaan dan pertidaksamaan dengan contoh soal yang relevan.

1. Alpian Ariesta (0800297)

2. Peta konsep

3. SK & KD
Standar Kompetensi
 Memahami bentuk persamaan, dan pertidaksamaan
linier satu variabel.
 Menggunakan persamaan dan pertidaksamaan linier
satu variabel dalam pemecahan masalah.
Kompetensi Dasar
 Menyelesaikan persamaan linier satu variabel.
 Menyelesaikan pertidaksamaan linier satu variabel

4. Perhatikan kalimat berikut!
 Jakarta adalah ibu kota Indonesia, bernilai benar
 Tugu Monas terletak di Yogyakarta, bernilai salah
Kalimat yang dapat ditentukan nilai kebenarannya
(bernilai benar atau salah) disebut pernyataan.

5. Dapatkah Anda menjawab pertanyaan “Indonesia terletak
di Benua x ”.
Jika x diganti Asia maka kalimat tersebut bernilai benar.
Adapun jika x diganti Eropa maka kalimat tersebut bernilai
salah. Kalimat seperti “Indonesia terletak di Benua x” disebut
kalimat terbuka.
Contoh lainnya:
3 dikurang “suatu bilangan” hasilnya adalah 6, dapat ditulis:
 3 – x = 6, (misal x adalah ”suatu bilangan”)

6.  Kalimat terbuka adalah kalimat yang belum tentu nilai
kebenarannya.
 Variabel adalah lambang (simbol) pada kalimat terbuka
yang dapat diganti oleh sebarang anggota himpunan yang
telah ditentukan.
 Konstanta adalah nilai tetap (tertentu) yang terdapat pada
kalimat terbuka.
 Himpunan penyelesaian dari kalimat terbuka adalah
himpunan semua pengganti dari variabel-variabel pada
kalimat terbuka sehingga kalimat tersebut bernilai benar.

7. Persamaan Linear Satu Variabel
Perhatikan kalimat terbuka x + 1 = 5.
kalimat terbuka yang dihubungkan oleh tanda sama dengan
(“=“) disebut persamaan.
Persamaan dengan satu variabel berpangkat satu atau
berderajat satu disebut persamaan linear satu variabel.
Jadi,
Persamaan linear satu variabel adalah kalimat terbuka yang
dihubungkan oleh tanda sama dengan (“=“) dan hanya mempunyai satu
variabel berpangkat satu.

8. Contoh:
a. 2x – 3 = 5 (PLSV)
b. x2 – x = 2 (bukan PLSV)
c. 1/3 x = 1 5 (PLSV)

9. Himpunan Penyelesaian PLSV
Penyelesaian persamaan linear satu variabel dapat diperoleh dengan cara
substitusi,
Contoh:
Tentukan himpunan penyelesaian dari persamaan x + 4 = 7, jika x variabel pada
himpunan bilangan cacah.
Penyelesaian:
Jika x diganti bilangan cacah, diperoleh
substitusi x = 0, maka 0 + 4 = 7 (kalimat salah)
substitusi x = 1, maka 1 + 4 = 7 (kalimat salah)
substitusi x = 2, maka 2 + 4 = 7 (kalimat salah)
substitusi x = 3, maka 3 + 4 = 7 (kalimat benar)
substitusi x = 4, maka 4 + 4 = 8 (kalimat salah)
Ternyata untuk x = 3, persamaan x + 4 = 7 menjadi kalimat yang benar.
Jadi, himpunan penyelesaian persamaan x + 4 = 7 adalah {3}.
Tapi apakah setiap persamaan Linear satu variabel dapat diselesaikan dengan cara
substitusi??

10. Persamaan Persamaan yang Ekuivalen
Perhatikan uraian berikut.
a. x – 3 = 5
Jika x diganti bilangan 8 maka 8 – 3 = 5 (benar). Jadi, penyelesaian persamaan x – 3 =
5
adalah x = 8.
b. 2x – 6 = 10 (kedua ruas pada persamaan a dikalikan 2)
Jika x diganti bilangan 8 maka 2(8) – 6 = 10
↔ 16 – 6 = 10 (benar).
Jadi, penyelesaian persamaan 2x – 6 = 10 adalah x = 8.
c. x + 4 = 12 (kedua ruas pada persamaanya ditambah 7)
Jika x diganti bilangan 8 maka 8 + 4 = 12 (benar).
Jadi, penyelesaian persamaan x + 4 = 12 adalah x = 8.
ketiga persamaan mempunyai penyelesaian yang sama, yaitu x = 8. Persamaan-
persamaan di atas disebut persamaan yang ekuivalen.
Suatu persamaan yang ekuivalen dinotasikan dengan “↔ ”.
Dengan demikian bentuk x – 3 = 5; 2x – 6 = 10; dan x + 4 = 12 dapat dituliskan
sebagai
x – 3 = 5 ↔ 2x – 6 = 10 ↔ x + 4 = 12.

11. Jadi, dapat dikatakan sebagai berikut
Dua persamaan atau lebih dikatakan ekuivalen jika mempunyai
himpunan penyelesaian yang sama dan dinotasikan dengan tanda “↔ ”.
Perhatikan uraian berikut
x–5=4
↔x–5+5=4+5
↔ x=9
Jadi, himpunan penyelesaian persamaan x – 5 = 4 adalah {9}. Dengan kata
lain, persamaan x – 5 = 4 ekuivalen dengan persamaan x = 9, atau
ditulis
x – 5 = 4 ↔ x = 9.
Suatu persamaan dapat dinyatakan ke dalam persamaan yang ekuivalen
dengan cara:
a. menambah atau mengurangi kedua ruas dengan bilangan yang sama;
b. mengalikan atau membagi kedua ruas dengan bilangan yang sama.

12. Contoh soal
EBTANAS SMP tahun 1993 nomer 03
Jika diketahui x + 5 = 11, maka nilai x + 33 adalah …
A. 19
B. 29
C. 39
D. 49
Jawab
Cari terlebih dahulu nilai x
x + 5 = 11
↔x + 5 – 5 = 11 – 5
↔x = 6
didapat penyelesaian x = 6, kemudian x + 33 = 6 + 33 = 39.
Jadi jawaban untuk soal diatas adalah opsi C

13. Contoh Soal 2
EBTANAS SMP tahun 2001 no. 12
Himpunan penyelesaian dari, jika x variabel pada himpunan
bilangan pecahan adalah …
A. { }
B. { }
C. { }
D. { }
Jawab

14. Ketidaksamaan
Dalam kehidupan sehari-hari kita sering menemukan kalimat
seperti berikut:
a. Sadam memiliki berat badan lebih dari 50 kg.
b. Sebuah Damri dapat mengangkut tidak lebih dari 55 orang
Dalam kalimat matematika:
a. Misal x adalah berat badan sadam (dalam Kg), x lebih dari 50
ditulis x > 50
b. Misal y adalah daya angkut damri dalam satuan jumlah orang, y
tidak lebih dari 55 ditulis y ≤ 55
Kalimat-kalimat x > 50 dan y ≤ 55 termasuk konsep ketidaksamaan

15. Suatu ketidaksamaan selalu ditandai dengan salah satu tanda
hubung berikut.
“<” untuk menyatakan kurang dari.
“>” untuk menyatakan lebih dari.
“ ≤ ” untuk menyatakan tidak lebih dari atau kurang dari
atau sama dengan.
“ ≥ ” untuk menyatakan tidak kurang dari atau lebih dari
atau sama dengan.

16. Pertidaksamaan Linear Satu
Variabel
Kalimat terbuka yang menyatakan hubungan ketidaksamaan
(<, >, ≤ , atau ≥ ) disebut pertidaksamaan.
Pertidaksamaan linear satu variabel adalah pertidaksamaan
yang hanya mempunyai satu variabel dan berpangkat satu
(linear).
Contoh
 a. x – 3 < 5 ( PtLSV )
 b. a ≤ 1 – 2b ( bukan PtLSV )
 c. x2 – 3x ≥ 4 ( bukan PtLSV )

17. Penyelesaian PtLSV
Perhatikan pertidaksamaan 10 – 3x > 2, dengan x variabel pada himpunan bilangan asli.
Jika x diganti 1 maka 10 – 3x > 2
↔ 10 – 3 . 1 > 2
↔ 7 > 2 (pernyataan benar)
Jika x diganti 2 maka 10 – 3x > 2
↔ 10 – 3 . 2 > 2
↔ 4 > 2 (pernyataan benar)
Jika x diganti 3 maka 10 – 3x > 2
↔ 10 – 3 . 3 > 2
↔ 1 > 2 (pernyataan salah)
Jika x diganti 4 maka 10 – 3x > 2
↔ 10 – 3 . 4 > 2
↔ –2 > 2 (pernyataan salah)
Ternyata untuk x = 1 dan x = 2, pertidaksamaan 10 – 3x > 2
menjadi kalimat yang benar. Jadi, himpunan penyelesaian dari
10 – 3x > 2 adalah {1, 2}.
Secara umum dapat dituliskan Pengganti variabel dari suatu pertidaksamaan, sehingga menjadi
pernyataan yang benar disebut penyelesaian dari pertidaksamaan
linear satu variabel.

18.  Contoh:
Tentukan himpunan penyelesaian dari pertidaksamaan 4x – 2 > 3x + 5 dengan x
variabel pada himpunan bilangan cacah.
Jawab
Cara 1
4x – 2 > 3x + 5
↔ 4x – 2 + 2 > 3x + 5 + 2 (kedua ruas ditambah 2)
↔ 4x > 3x + 7
↔ 4x + (–3x) > 3x + (–3x) + 7 (kedua ruas ditambah –3x)
↔ x>7
Karena x variabel pada himpunan bilangan cacah maka himpunan penyelesaiannya
adalah {8, 9, 10, ...}.
Cara 3
4x – 2 > 3x + 5
↔ 4x – 2 – 5 > 3x + 5 – 5 (kedua ruas dikurangi 5)
↔ 4x – 7 > 3x
↔ 4x + (–4x) – 7 > 3x + (–4x) (kedua ruas ditambah –4x)
↔ –7 > –x
↔ –7 : (–1) < –x : (–1) (kedua ruas dibagi dengan –1 tetapi tanda ketidaksamaan
berubah menjadi <)
↔ 7 < x atau x > 7
Karena x anggota bilangan cacah maka himpunan penyelesaiannya adalah {8, 9, 10, ...}.

19. Dari uraian tersebut dapat disimpulkan sebagai berikut:
Suatu pertidaksamaan dapat dinyatakan ke dalam pertidaksamaan
yang ekuivalen dengan cara sebagai berikut.
a. Menambah atau mengurangi kedua ruas dengan bilangan
yang sama tanpa mengubah tanda ketidaksamaan.
b. Mengalikan atau membagi kedua ruas dengan bilangan
positif yang sama tanpa mengubah tanda ketidaksamaan.
c. Mengalikan atau membagi kedua ruas dengan bilangan
negatif yang sama, tetapi tanda ketidaksamaan berubah,
dimana
1) > menjadi <; 3) < menjadi >;
2) ≤ menjadi ≥ ; 4) ≥ menjadi ≤.

20. Contoh soal
UN SMP tahun 2007 no. 8
Penyelesaian dari pertidaksamaan
adalah ...
A. x ≥ -17
B. x ≥ -1
C. x ≥ 1
D. x ≥ 17

21. Jawab
Jadi jawaban untuk soal diatas adalah opsi C