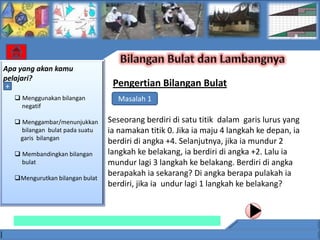
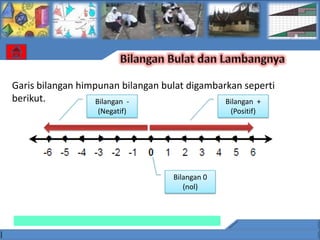
Dokumen tersebut membahas tentang standar kompetensi, kompetensi dasar, indikator pencapaian, materi pelajaran, dan uji kompetensi untuk pelajaran matematika SMP kelas VII yang mencakup bilangan bulat, operasi hitung pada bilangan bulat, dan sifat-sifat operasi hitung.


























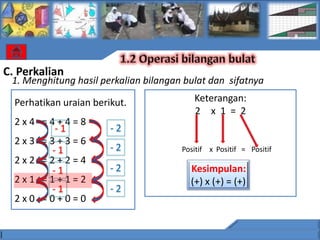
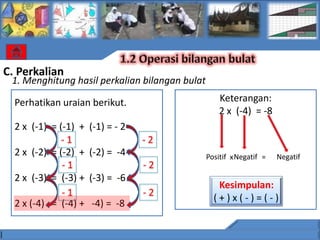
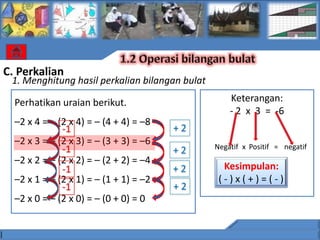
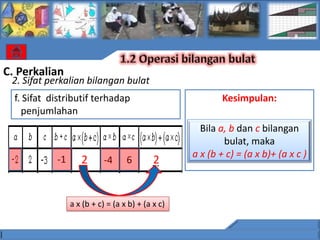
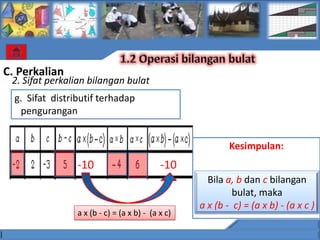
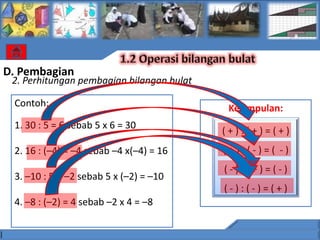
![C. Perkalian
1. Menghitung hasil perkalian bilangan bulat
Perhatikan uraian berikut. Keterangan:
- 2 x -(3) = 6
–2 x (-1)= – (2 x (-1)) = – [(-1) + (-1)] = 2
-1 +2
Negatif x Negatif = Positif
–2 x (-2) = –(2 x (-2))= – [(-2) + (-2) ]= 4
-1 +2 Kesimpulan:
–2 x (-3) = – (2 x (-3))= –[(-3) + (-3)] = 6 (-)x(-)=(+)
-1 +2
–2 x (-4)= – (2 x (-4)) = –[(-4) + (-4)] = 8](https://image.slidesharecdn.com/mediarinidaraini-110829192215-phpapp02/85/Bahan-Ajar-Bilangan-Bulat-31-320.jpg)