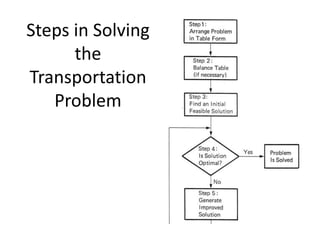
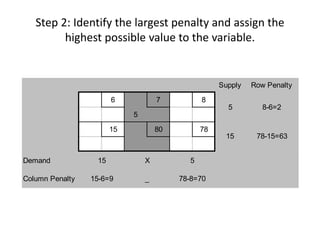
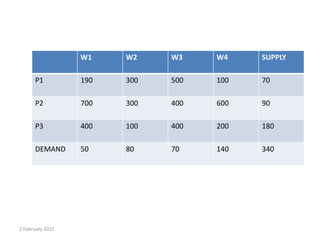
This document discusses transportation techniques and methods for solving transportation problems. It defines a transportation problem as aiming to find the best way to fulfill demand at multiple destinations using supply from multiple origins. It outlines the key components of a transportation model including origins, capacities, destinations, demands, and shipping costs. Three common solution methods are described - the minimum cost method, northwest corner method, and Vogel's approximation method - along with examples of each step. The document also lists some applications of transportation models like scheduling airlines and identifying facility locations.

1. Transportation Techniques
By Group 1
Shreeya
Sonia
Shweta
Shobha

2. Introduction
• A transportation problem basically deals with
the problem, which aims to find the best way
to fulfill the demand of n demand points using
the capacities of m supply points

3. A Transportation Model Requires
• The origin points, and the capacity or supply
per period at each
• The destination points and the demand per
period at each
• The cost of shipping one unit from each origin
to each destination

4. Terminology
• Balanced Transportation Problem
• Unbalanced Transportation Problem
• Transportation Table
• Dummy source or destination
• Initial feasible solution
• Optimum solution
• Objective function
• Constraint.

5. Transportation Problem Solutions steps
• Define problem
• Set up transportation table (matrix)
– Summarizes all data
– Keeps track of computations
• Develop initial solution
• Find optimal solution
• Assumption

6. Steps in Solving
the
Transportation
Problem

7. Warehouse
Source W1 W2 W3 W4 Supply
Capacity
F1 30 25 40 20 100
F2 29 26 35 40 250
F3 31 33 37 30 150
Demand 90 160 200 50 N = Total
supply/
Demand
Transportation Table

8. Special Issues in the Transportation
Model
• Demand not equal to supply
– Called ‘unbalanced’ problem
– Add dummy source if demand > supply
– Add dummy destination if supply > demand

9. There are three basic methods:
1. Minimum Cost Method
2. Northwest Corner Method
3. Vogel’s Method

10. Minimum Cost Method
Here, we use the following steps:
Step 1 Find the cell that has the least cost
Step 2: Assign as much as allocation to this cell
Step 3: Block those cells that cannot be allocated
Step 4: Repeat above steps until all allocation have been
assigned.

11. An example for Minimum Cost Method
Step 1: Select the cell with minimum cost.
2 3 5 6
2 1 3 5
3 8 4 6
5
10
15
12 8 4 6

12. Step 2: Cross-out column 2
2 3 5 6
2 1 3 5
8
3 8 4 6
12 X 4 6
5
2
15

13. Step 3: Find the new cell with minimum shipping cost
and cross-out row 2
2 3 5 6
2 1 3 5
2 8
3 8 4 6
5
X
15
10 X 4 6

14. Step 4: Find the new cell with minimum shipping cost
and cross-out row 1
2 3 5 6
5
2 1 3 5
2 8
3 8 4 6
X
X
15
5 X 4 6

15. Step 5: Find the new cell with minimum shipping cost
and cross-out column 1
2 3 5 6
5
2 1 3 5
2 8
3 8 4 6
5
X
X
10
X X 4 6

16. Step 6: Find the new cell with minimum shipping cost
and cross-out column 3
2 3 5 6
5
2 1 3 5
2 8
3 8 4 6
5 4
X
X
6
X X X 6

17. Step 7: Finally assign 6 to last cell. The bfs is found as:
X11=5, X21=2, X22=8, X31=5, X33=4 and X34=6
2 3 5 6
5
2 1 3 5
2 8
3 8 4 6
5 4 6
X
X
X
X X X X

18. Northwest corner method
Steps:
1. Assign largest possible allocation to the cell in
the upper left-hand corner of the table
2. Repeat step 1 until all allocations have been
assigned
3. Stop. Initial tableau is obtained
18

19. Vogel’s Approximation Method
• 1. Determine the penalty cost for each row and
column.
• 2. Select the row or column with the highest
penalty cost.
• 3. Allocate as much as possible to the feasible
cell with the lowest transportation cost in the row
or column with the highest penalty cost.
• 4. Repeat steps 1, 2, and 3 until all requirements
have been met.

20. An example for Vogel’s Method
Step 1: Compute the penalties.
Supply Row Penalty
6 7 8
15 80 78
Demand
Column Penalty 15-6=9 80-7=73 78-8=70
7-6=1
78-15=63
15 5 5
10
15

21. Step 2: Identify the largest penalty and assign the
highest possible value to the variable.
Supply Row Penalty
6 7 8
5
15 80 78
Demand
Column Penalty 15-6=9 _ 78-8=70
8-6=2
78-15=63
15 X 5
5
15

22. Step 3: Identify the largest penalty and assign the
highest possible value to the variable.
Supply Row Penalty
6 7 8
5 5
15 80 78
Demand
Column Penalty 15-6=9 _ _
_
_
15 X X
0
15

23. Step 5: Finally the bfs is found as X11=0, X12=5, X13=5,
and X21=15
Supply Row Penalty
6 7 8
0 5 5
15 80 78
15
Demand
Column Penalty _ _ _
_
_
X X X
X
X

24. Applications of
Transportation Model
• Scheduling airlines, including both planes and crew
• Deciding the appropriate place to site new facilities
such as a warehouse, factory or fire station
• Managing the flow of water from reservoirs
• Identifying possible future development paths for
parts of the telecommunications industry
• Establishing the information needs and appropriate
systems to supply them within the health service

26. 2 February 2015
W1 W2 W3 W4 SUPPLY
S1 10 20 5 7 10
S2 13 9 12 8 20
S3 4 15 7 9 30
S4 14 7 1 0 40
S5 3 12 5 19 50
DEMAND 60 60 20 10

27. W1 W2 W3 W4 SUPPLY
P1 190 300 500 100 70
P2 700 300 400 600 90
P3 400 100 400 200 180
DEMAND 50 80 70 140 340
2 February 2015