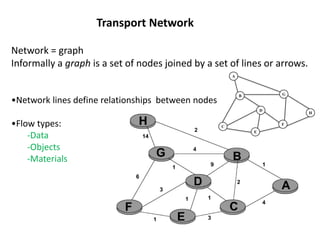
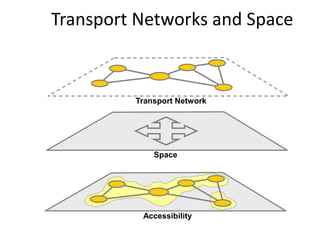
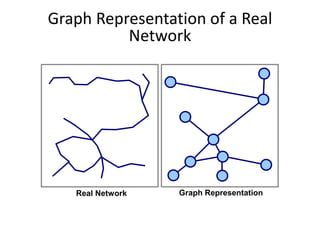
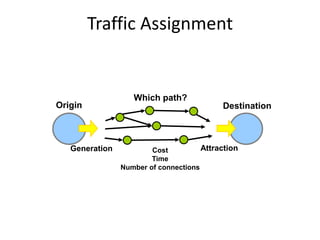
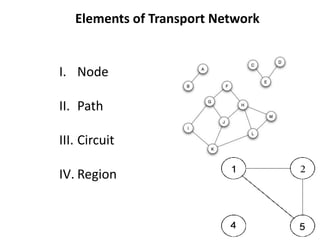
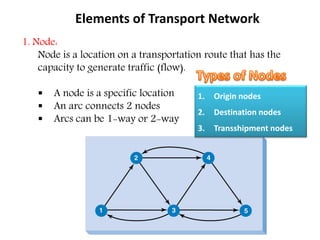
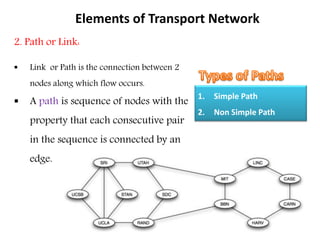
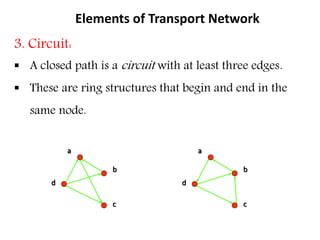
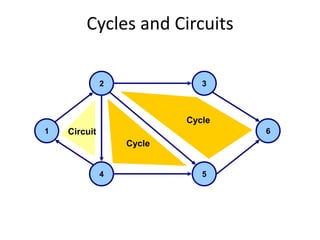
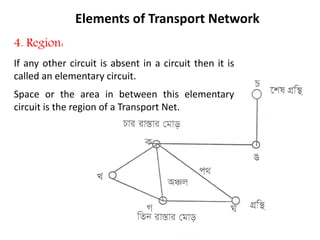
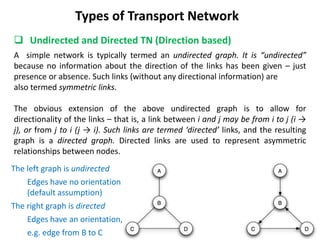
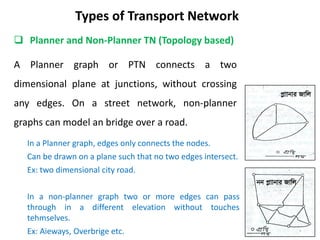
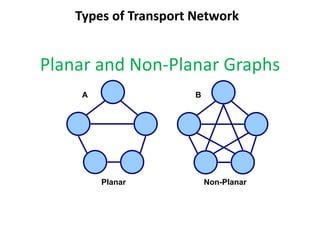
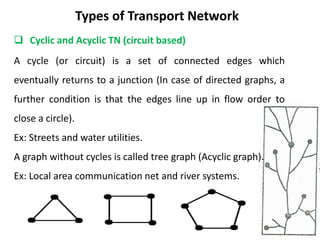
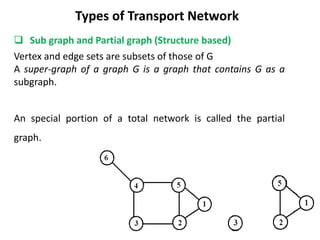
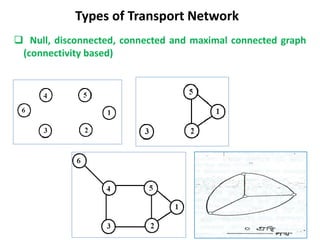
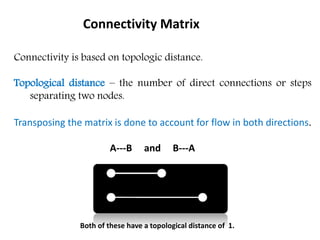
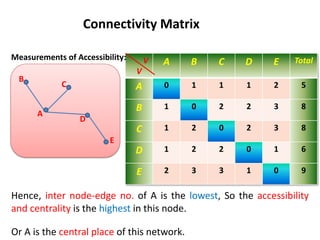
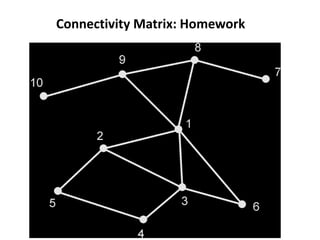
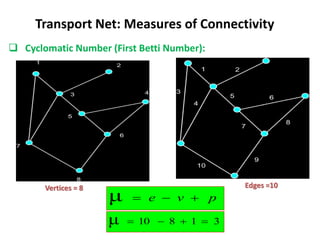
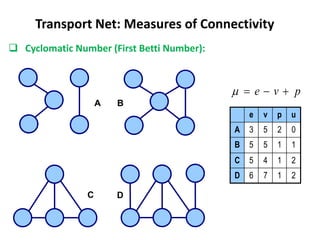
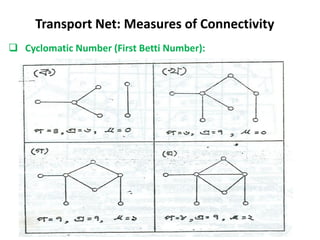
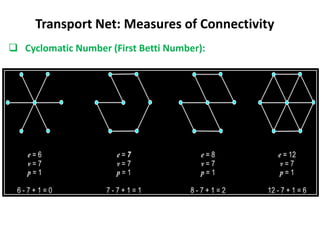
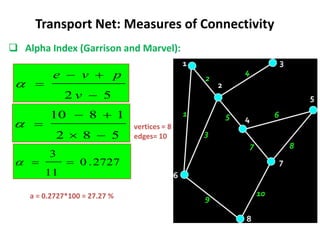
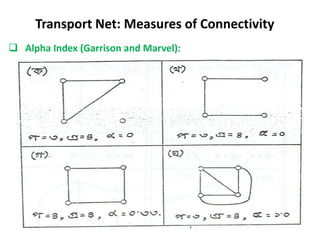
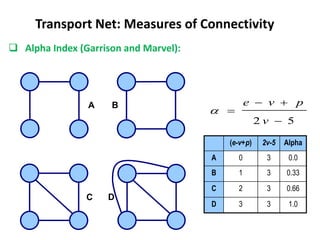
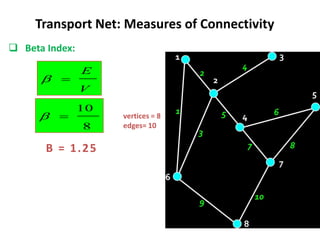
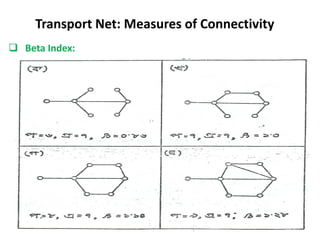
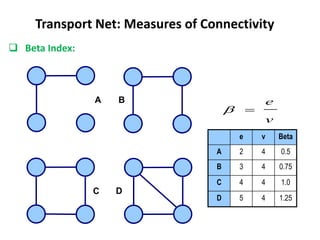
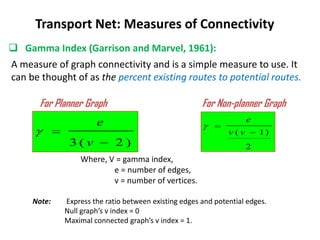
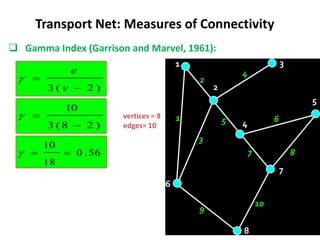
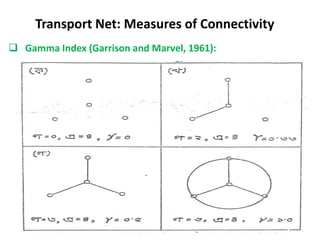
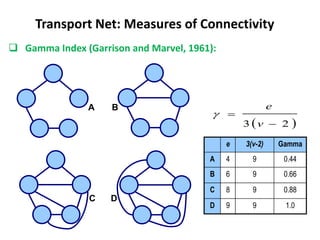
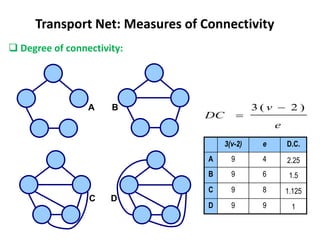
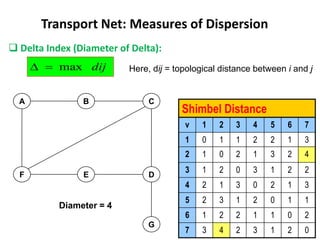
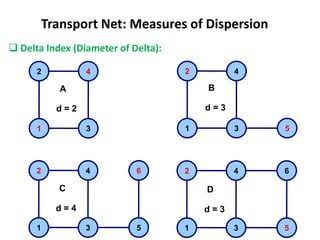
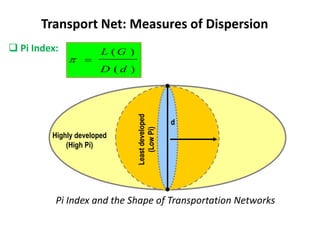
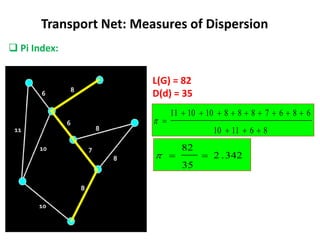
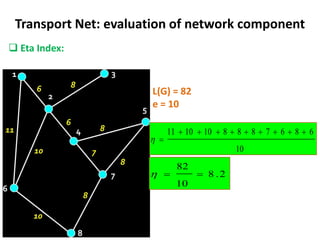
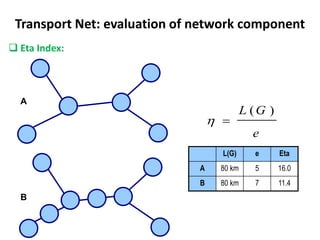
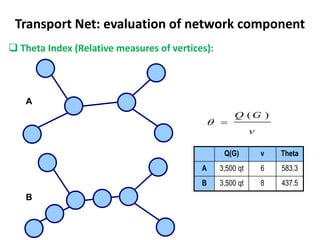
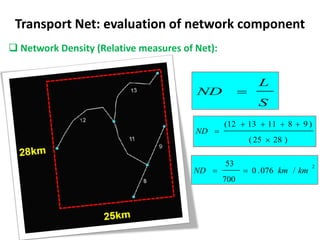
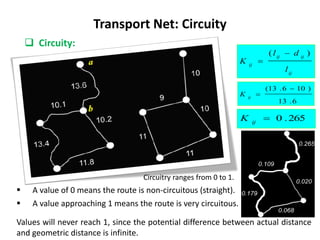
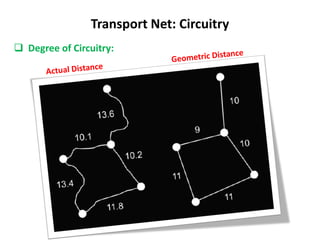
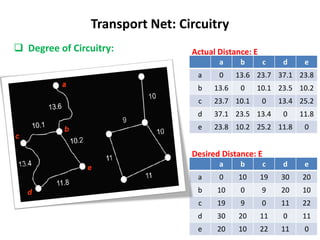
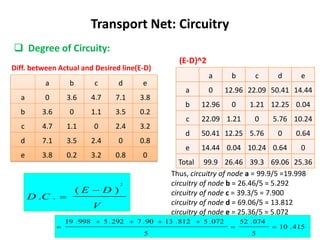
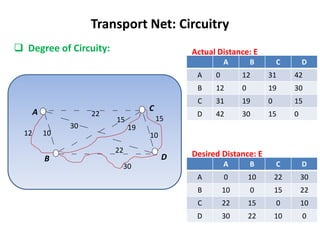
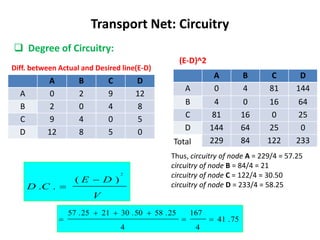
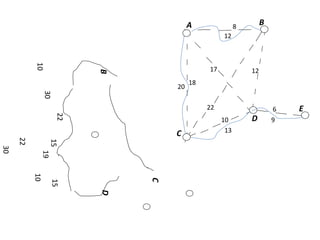
This document discusses transport networks and various measures used to analyze connectivity within networks. It defines key terms like nodes, links, paths and flows. There are four core components of a transportation system: modes, infrastructures, networks and flows. Different types of networks are described based on directionality, topology, presence of circuits and structure. Several graph-based measures are introduced to quantify connectivity within networks, including cyclomatic number, alpha index, beta index and gamma index. These indices examine aspects like ratio of existing circuits to potential circuits and average number of links per node. The document provides examples of calculating these measures for sample networks.