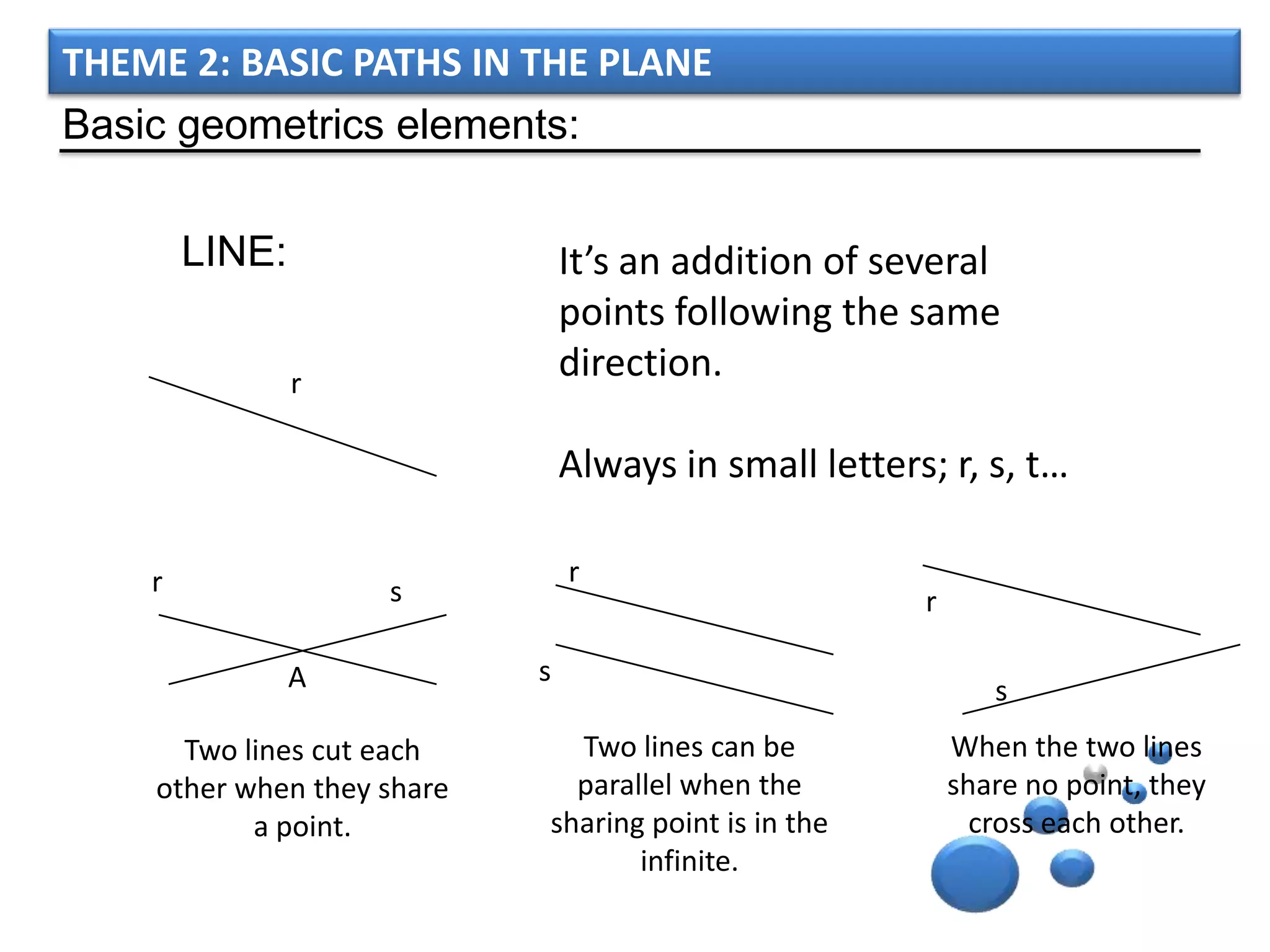
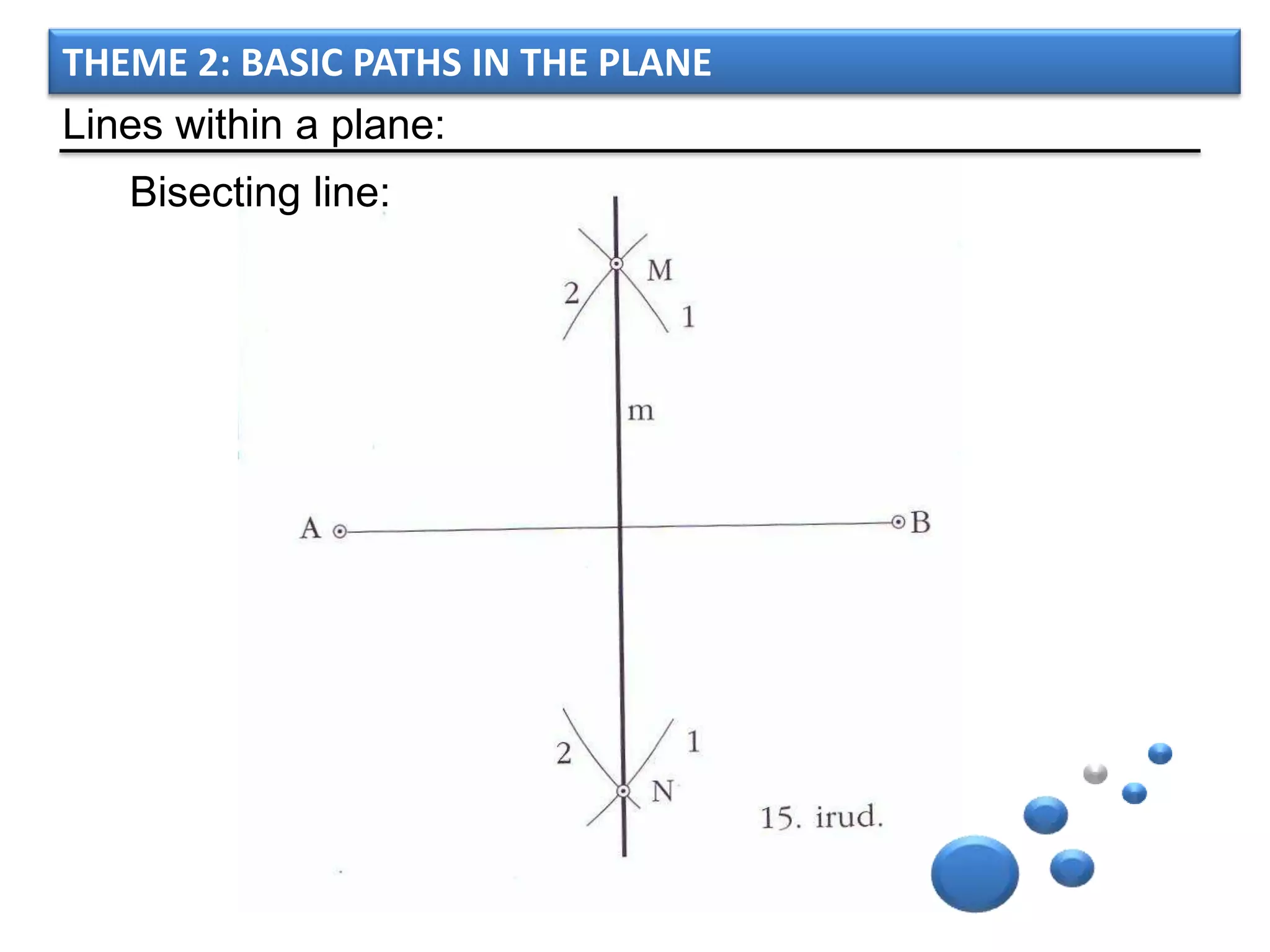
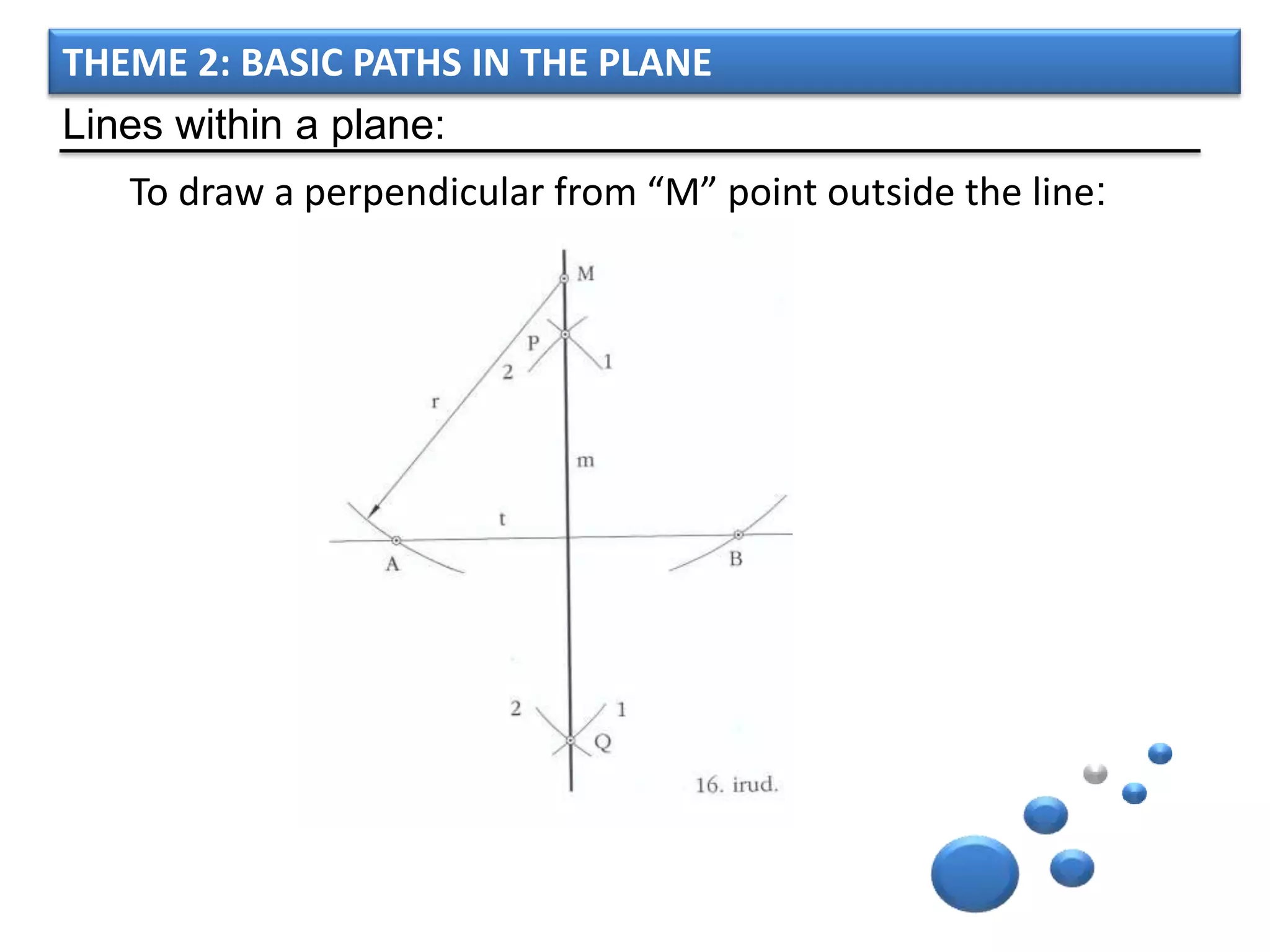
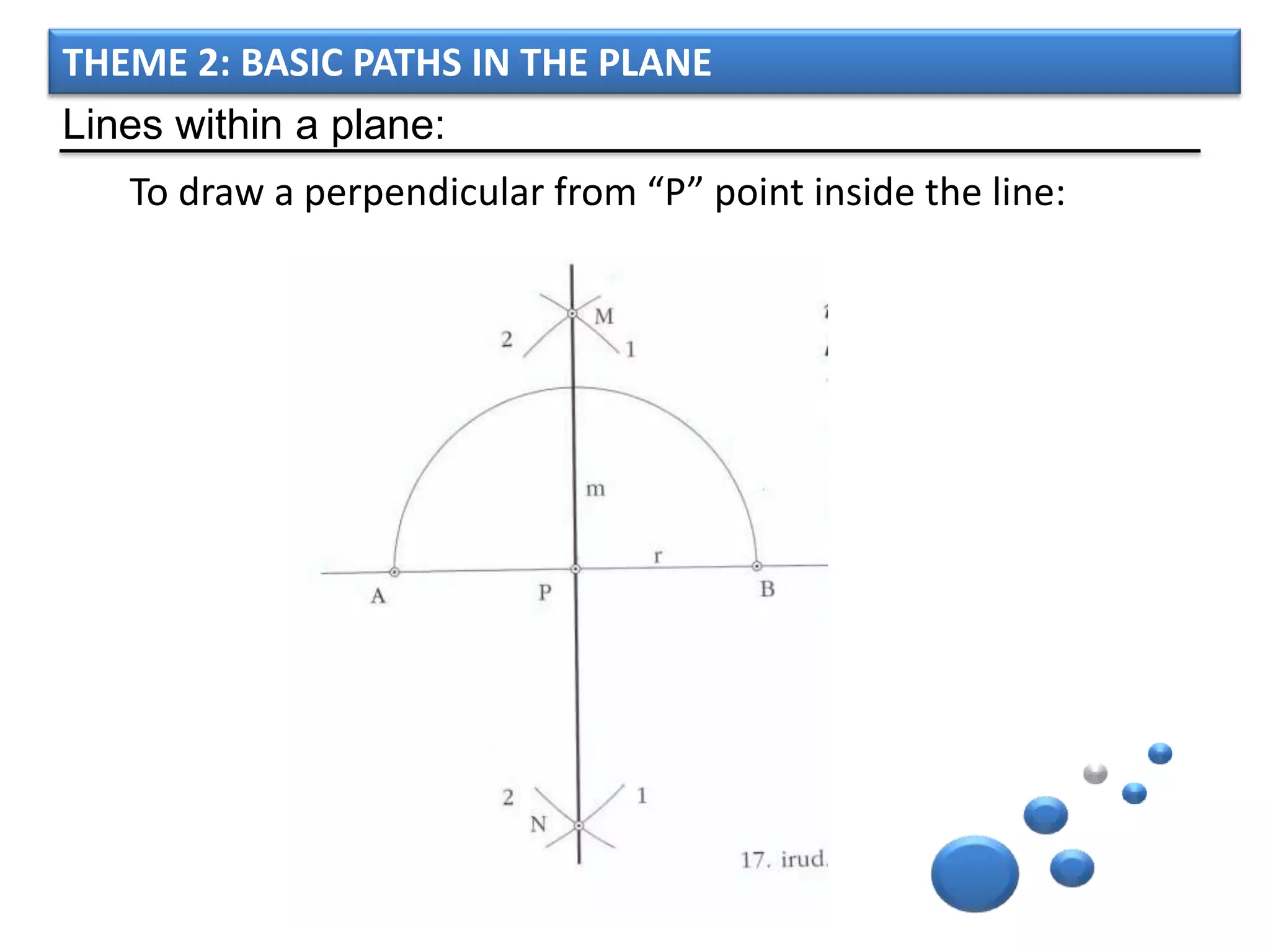
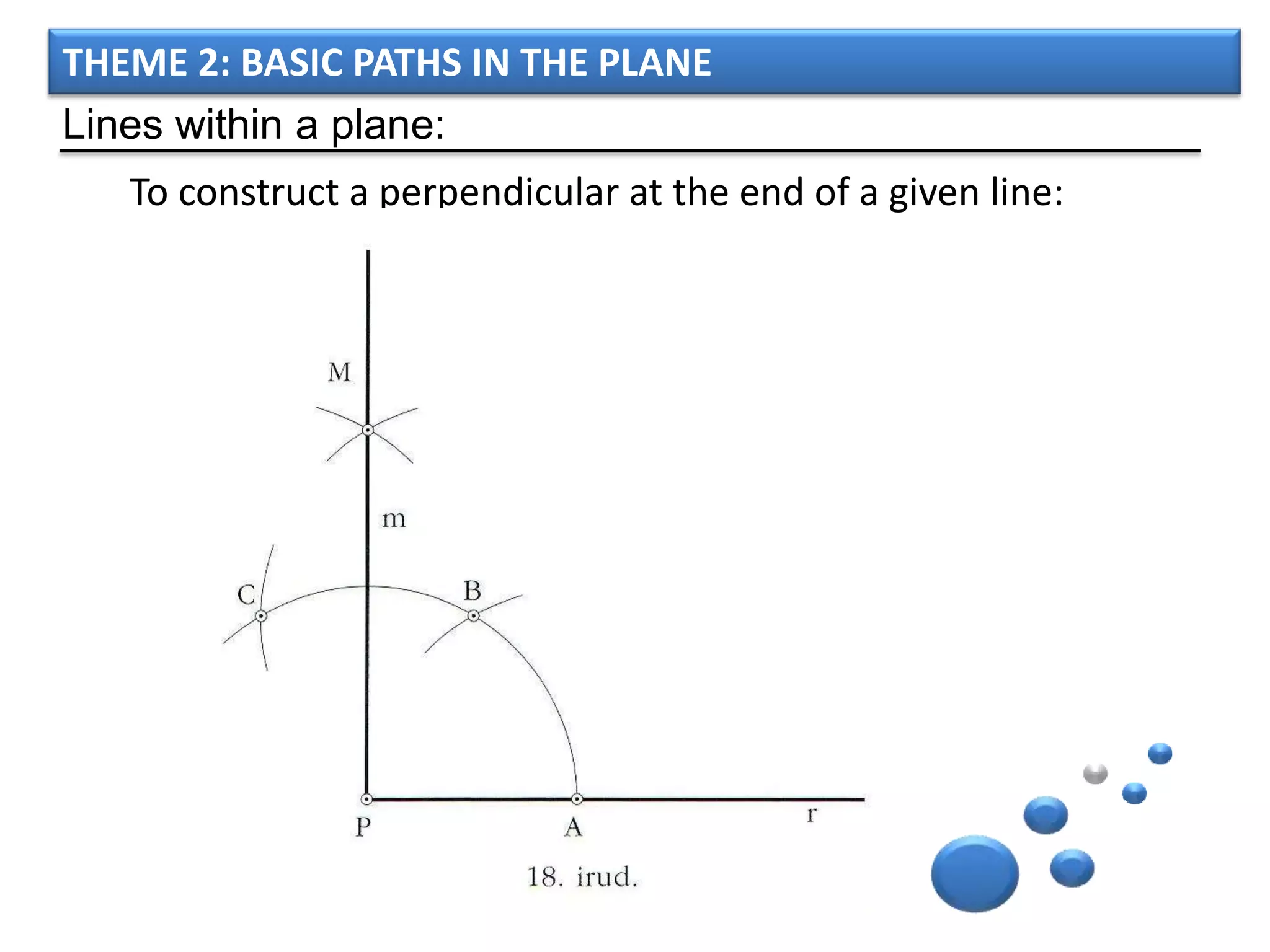
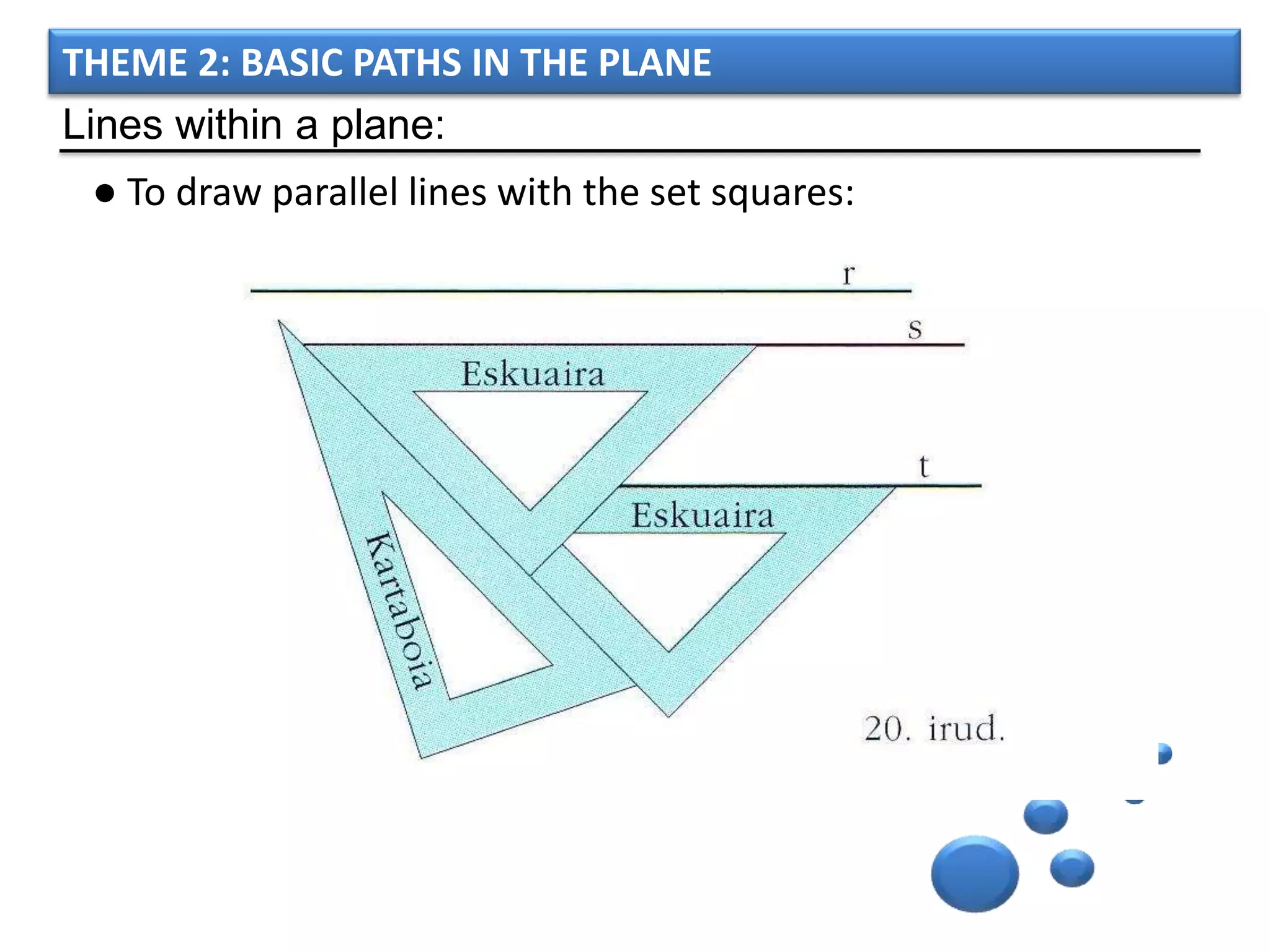
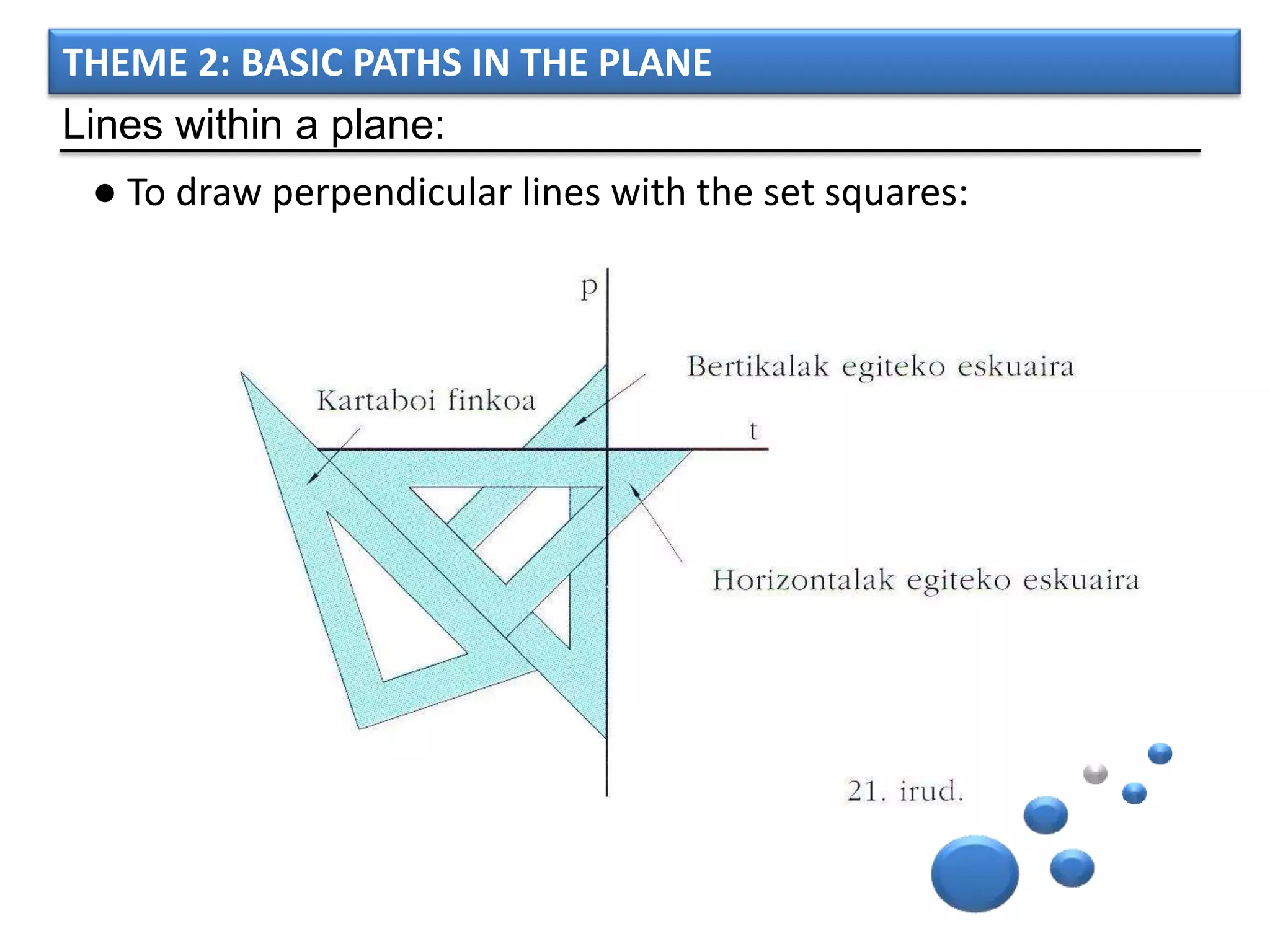
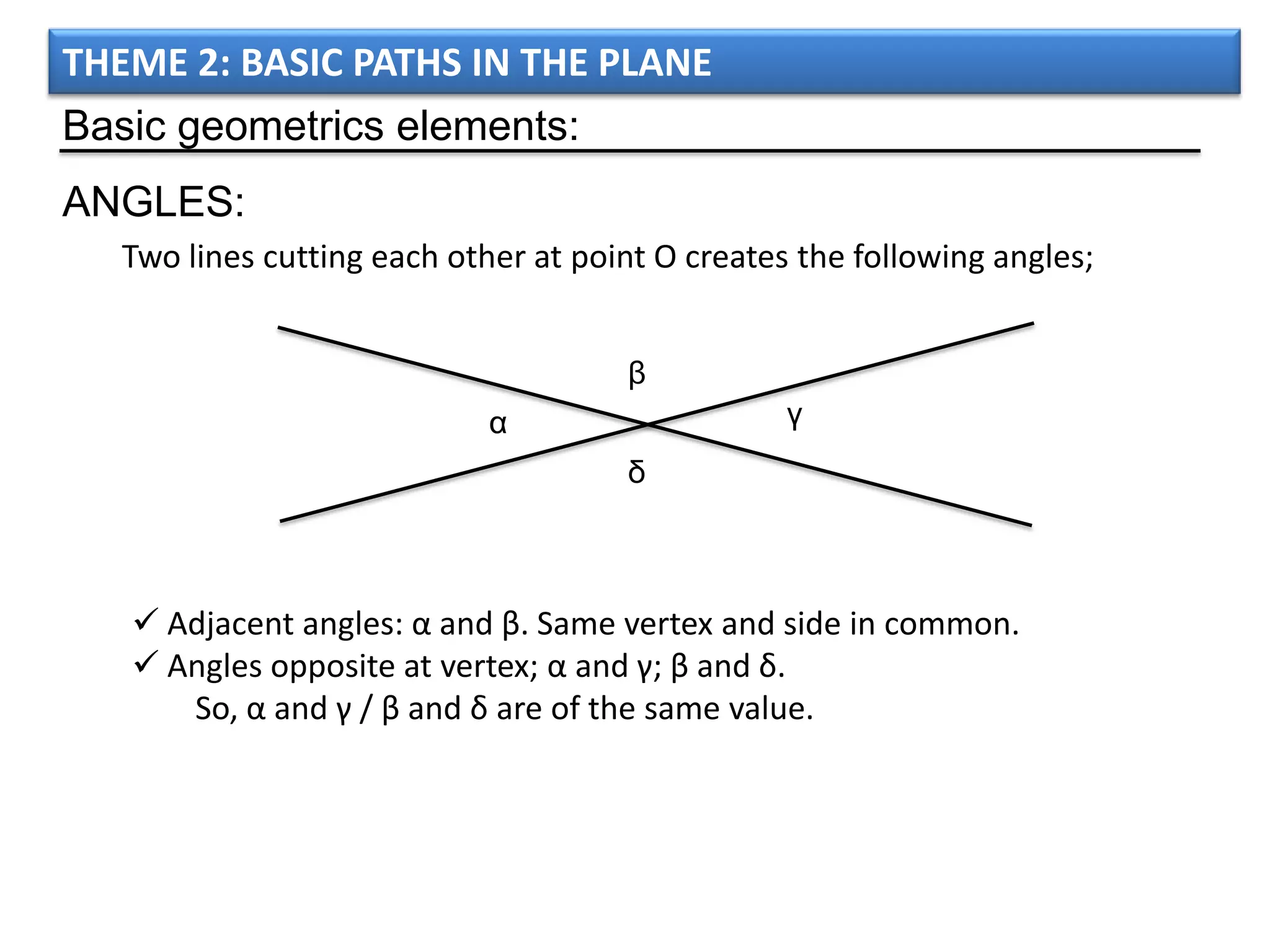
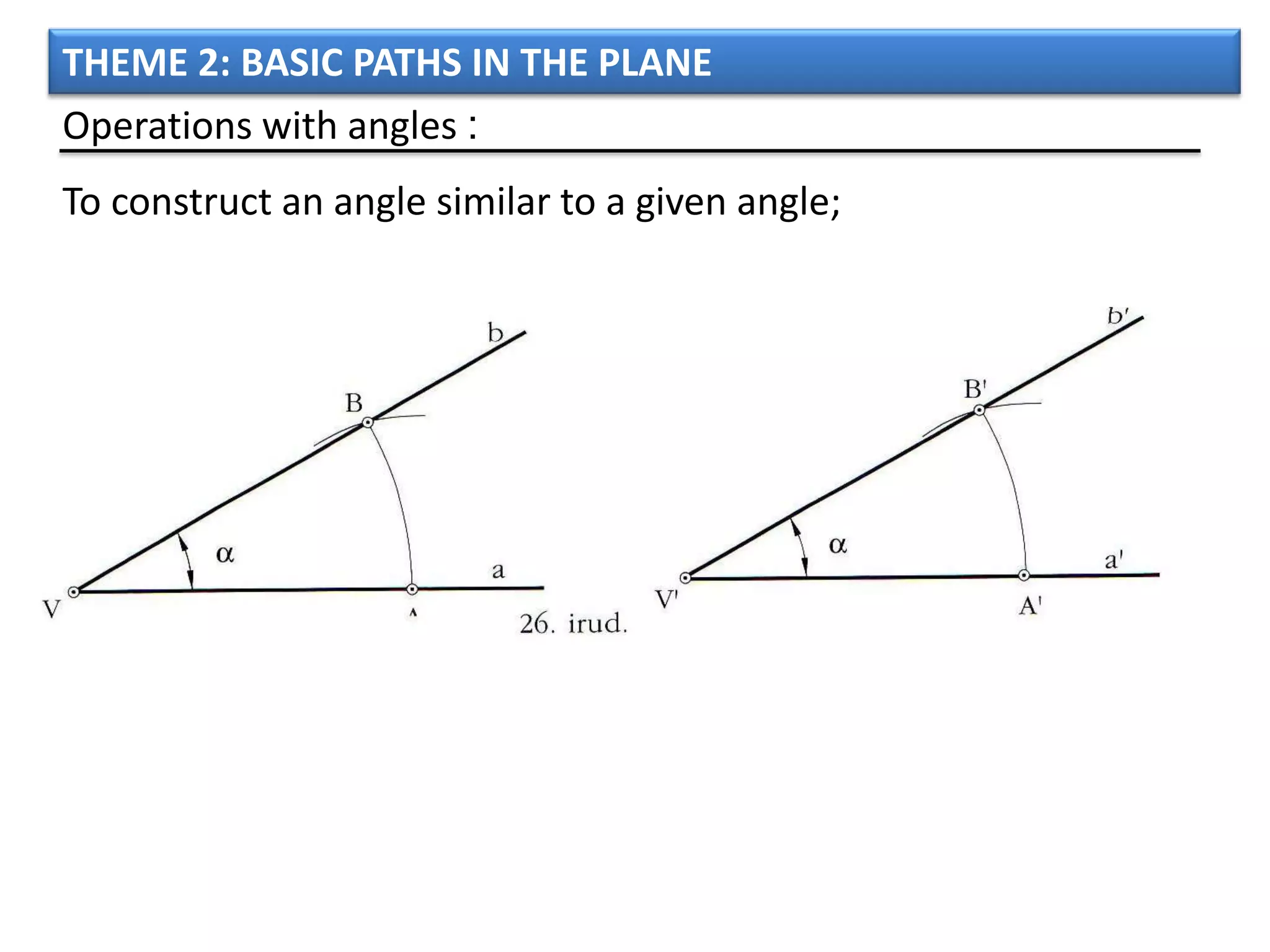
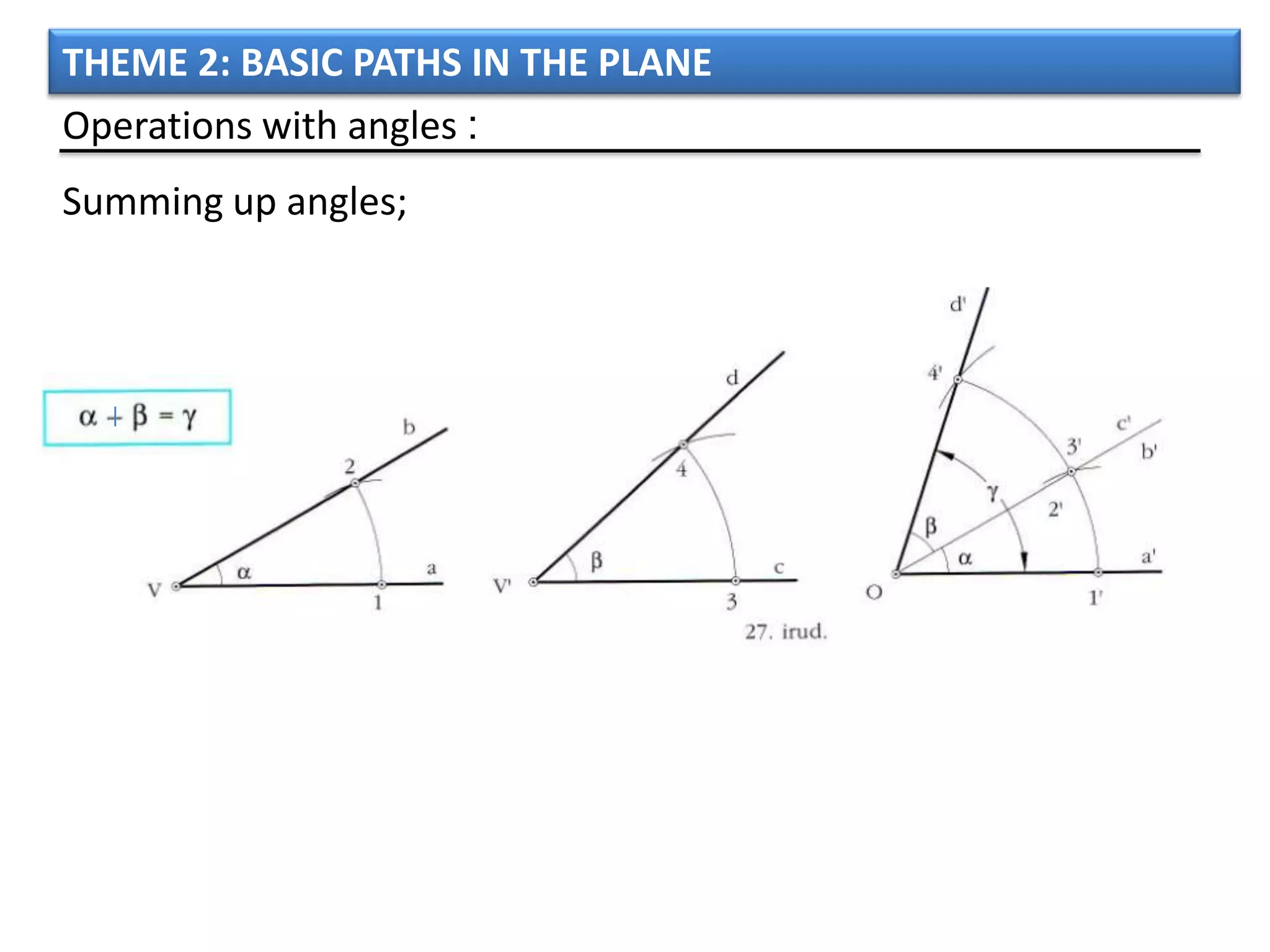
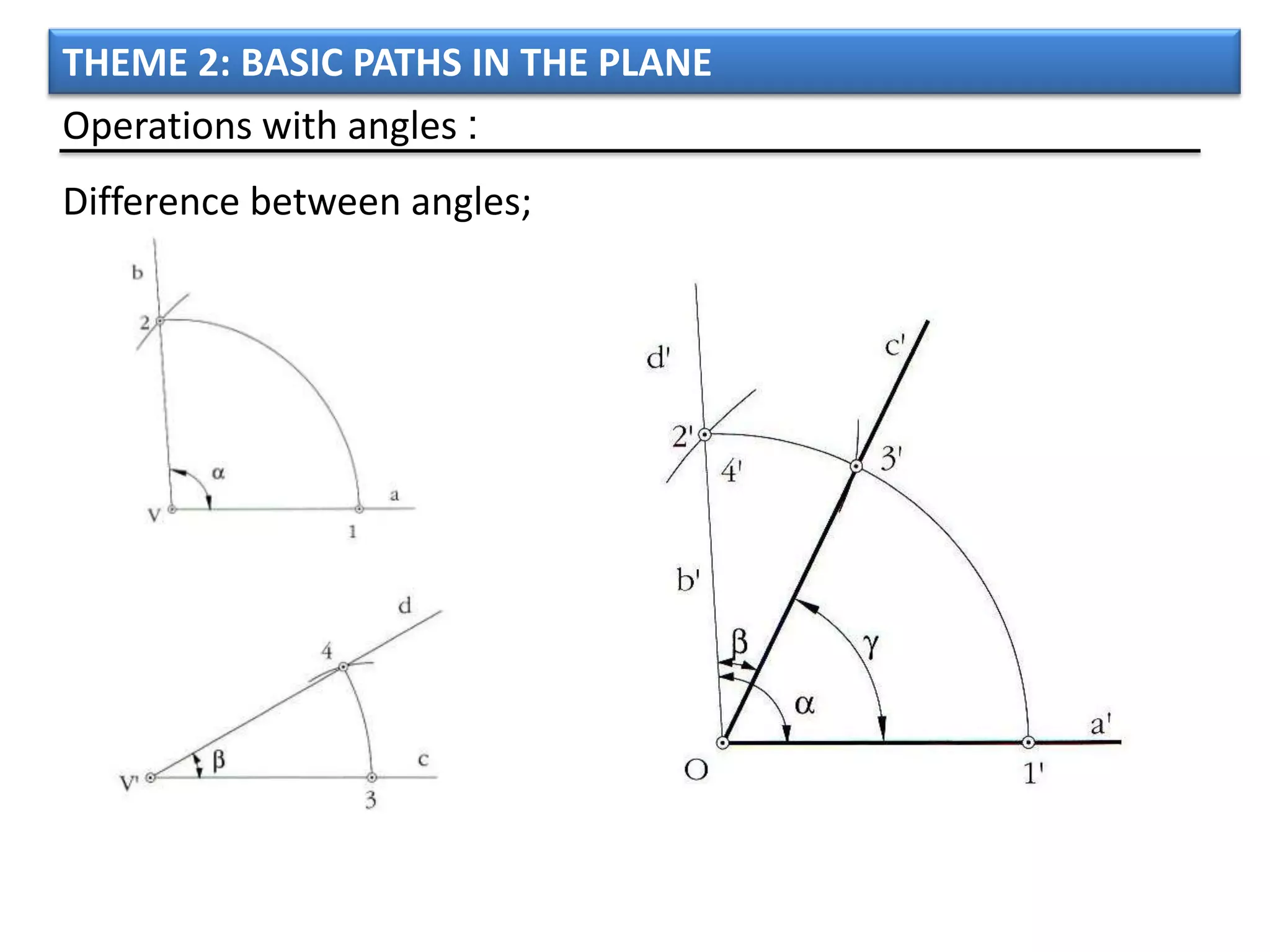
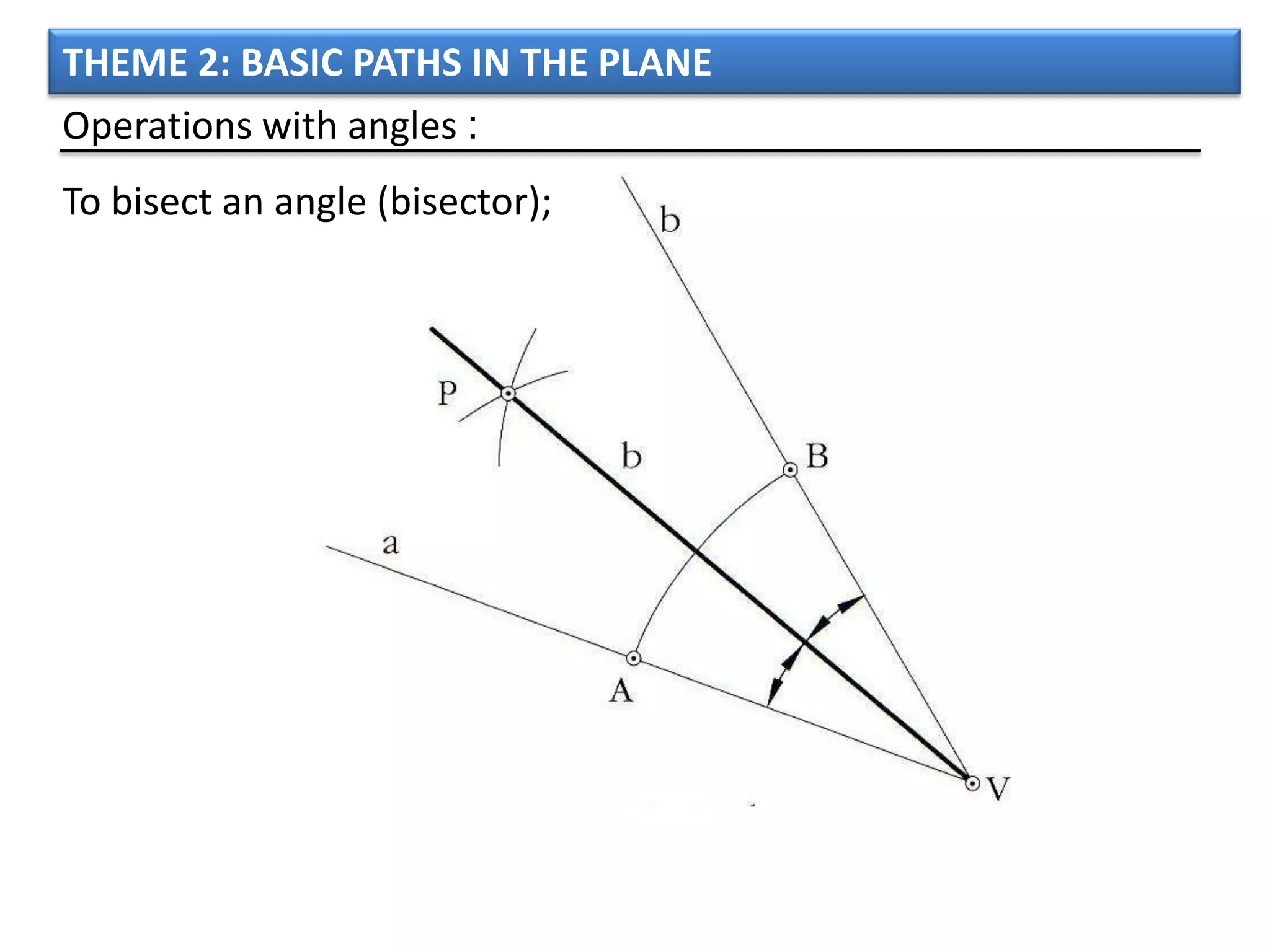
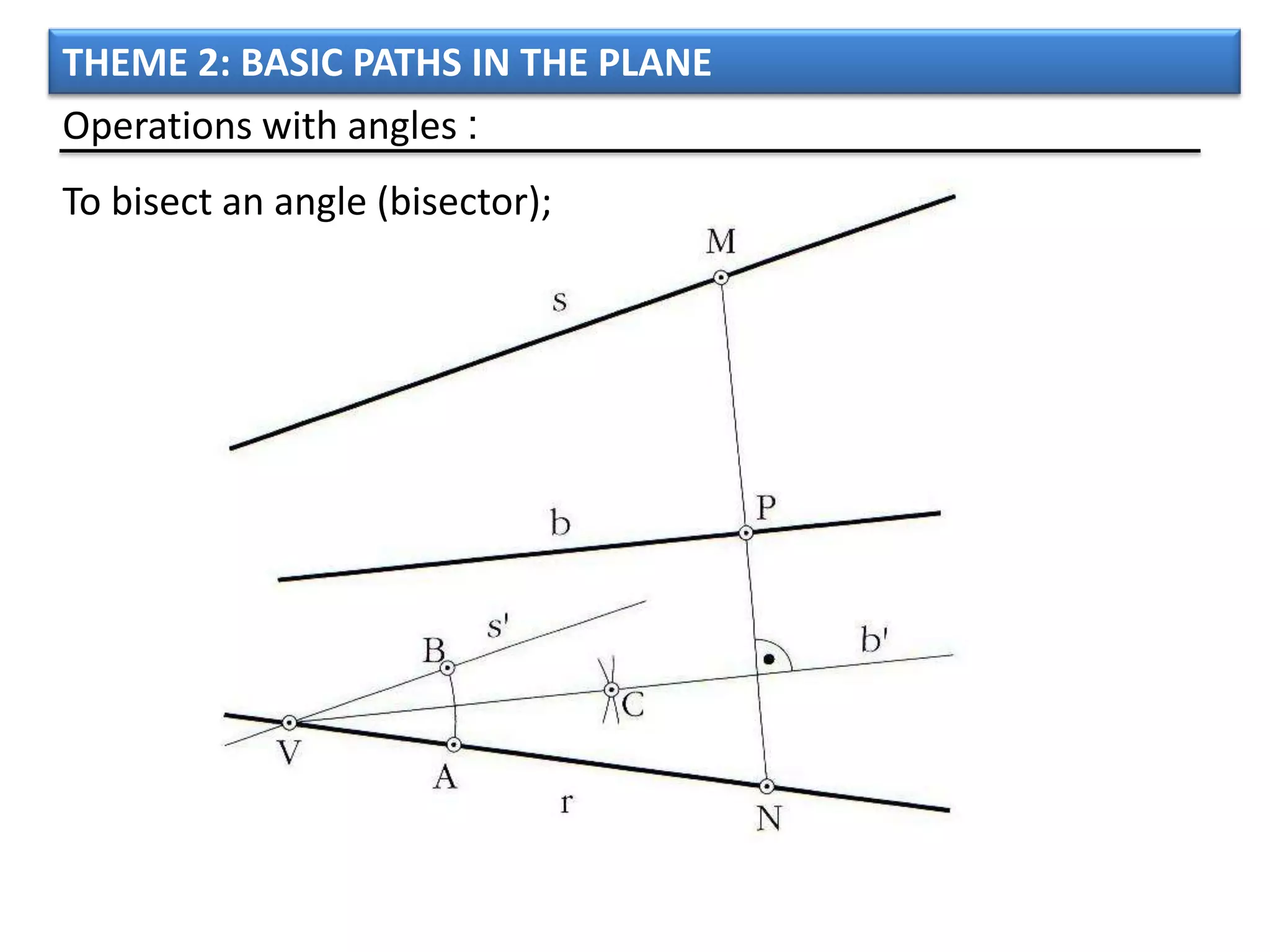
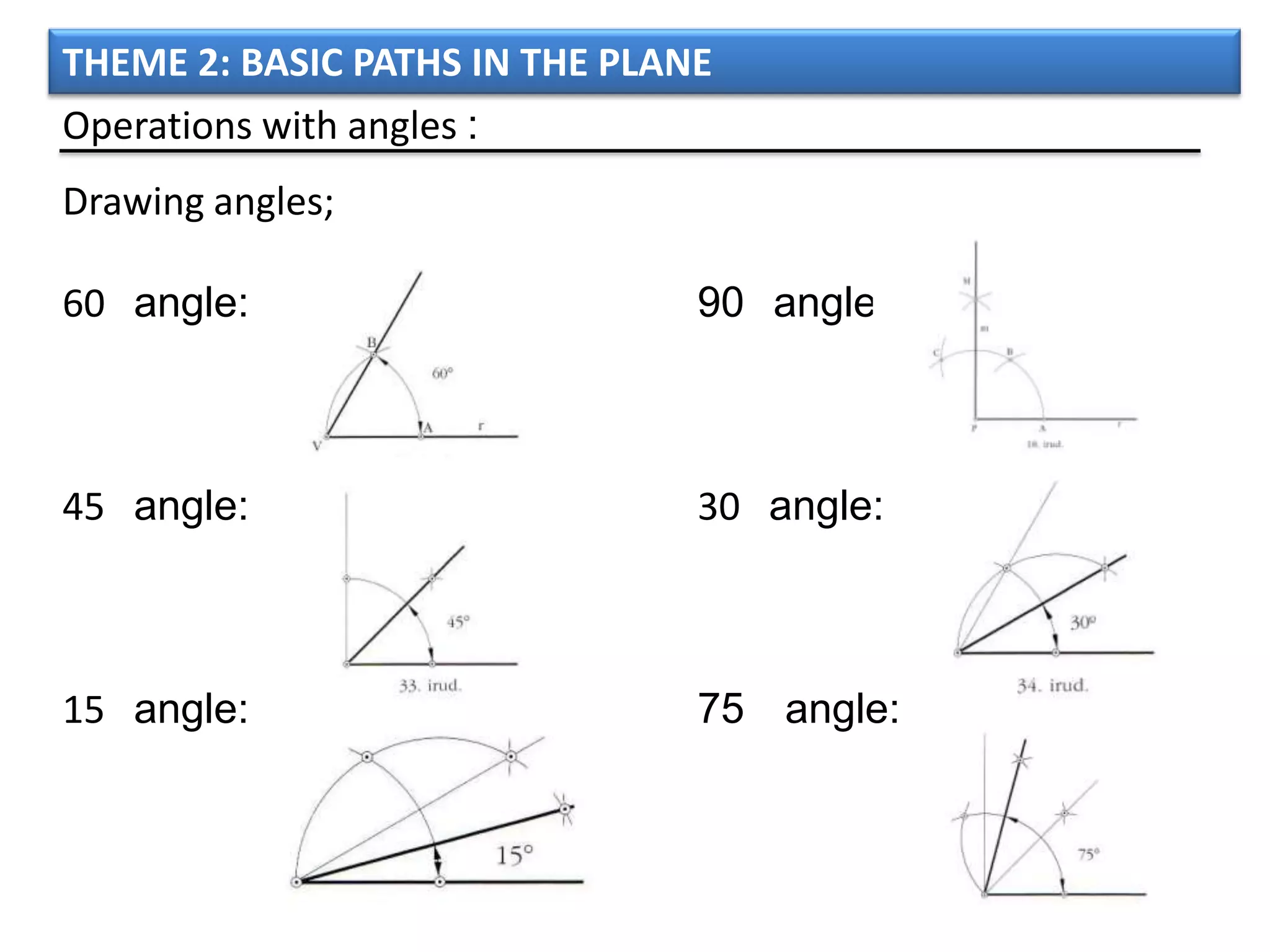
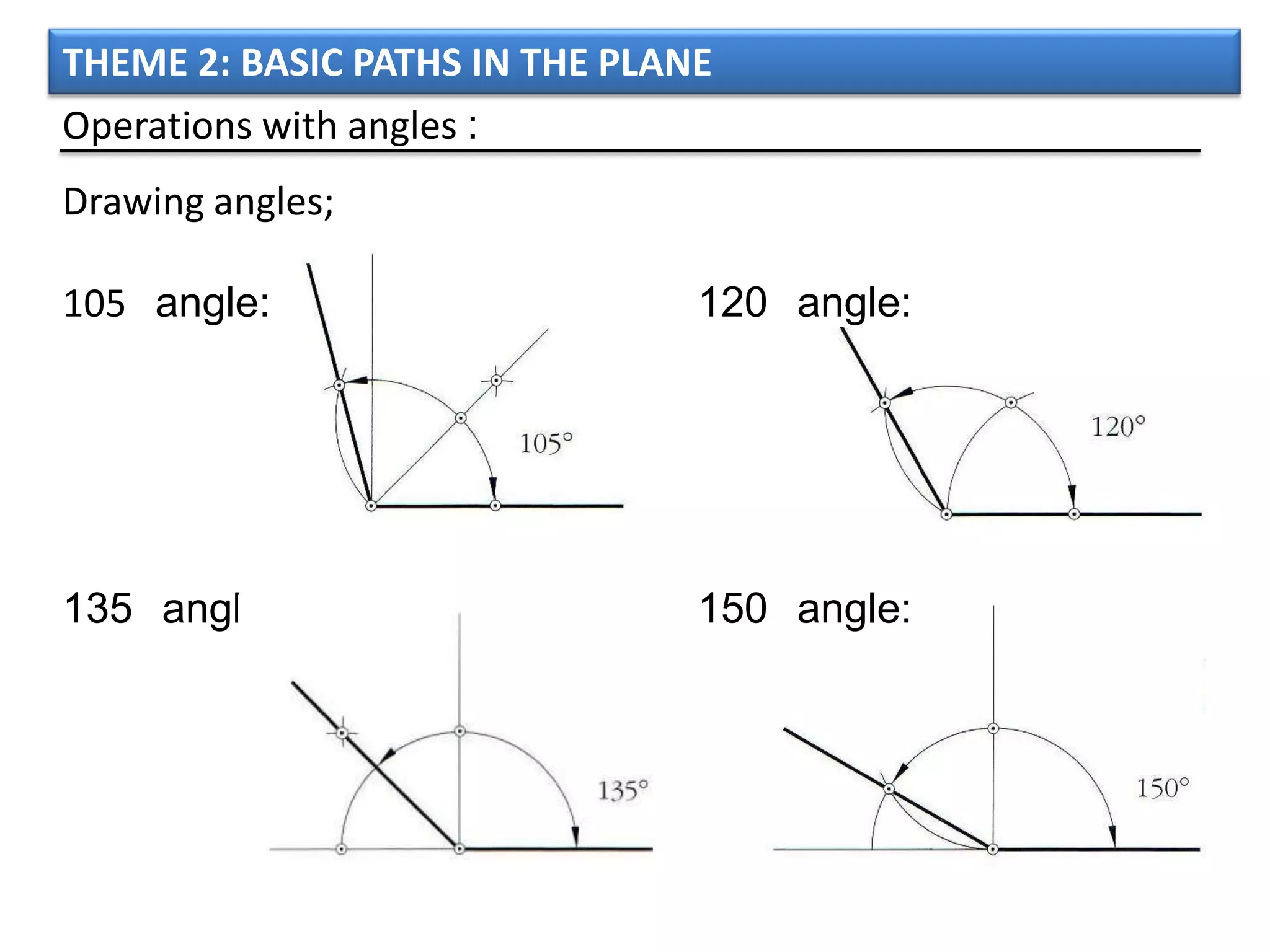
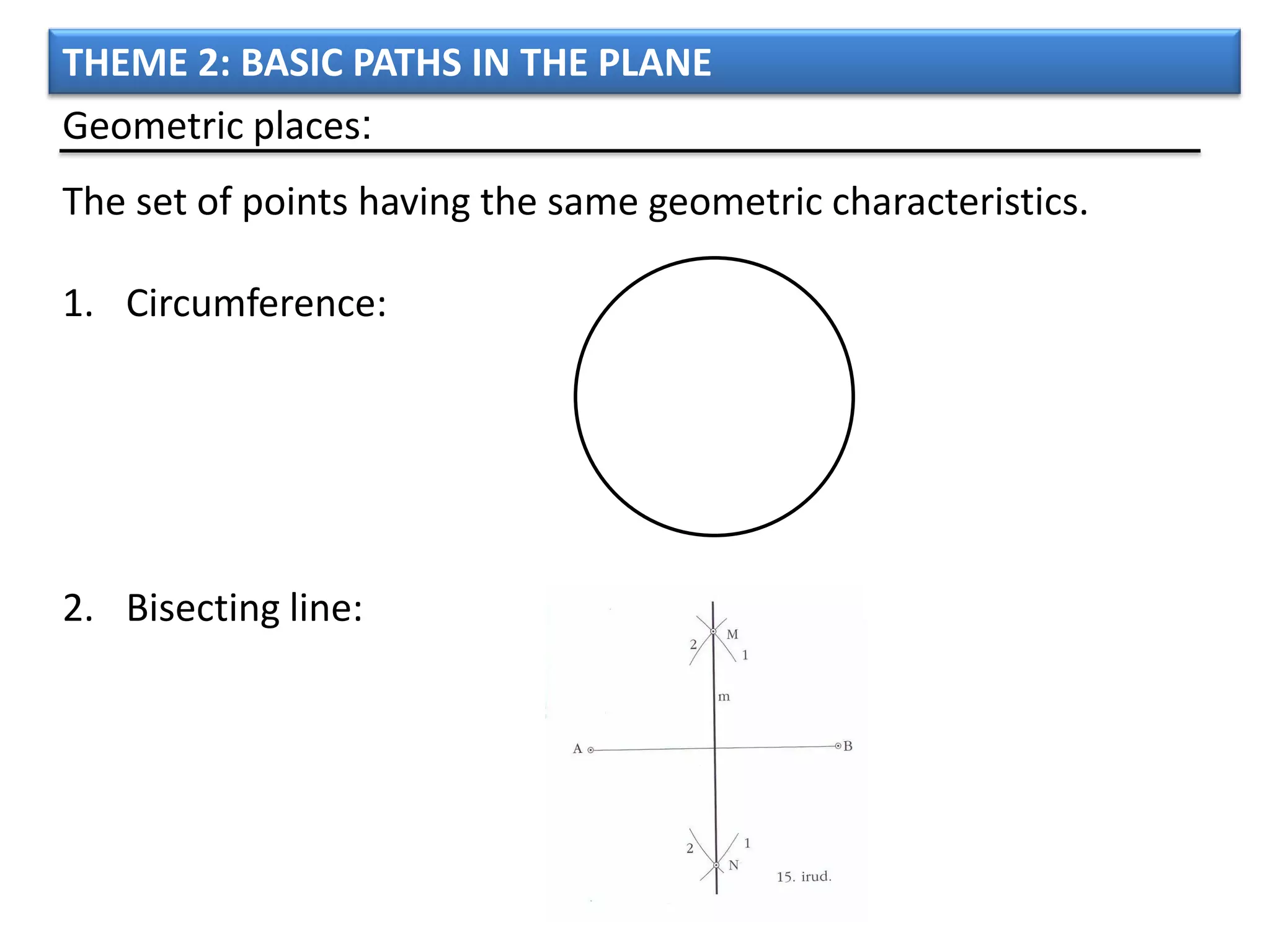
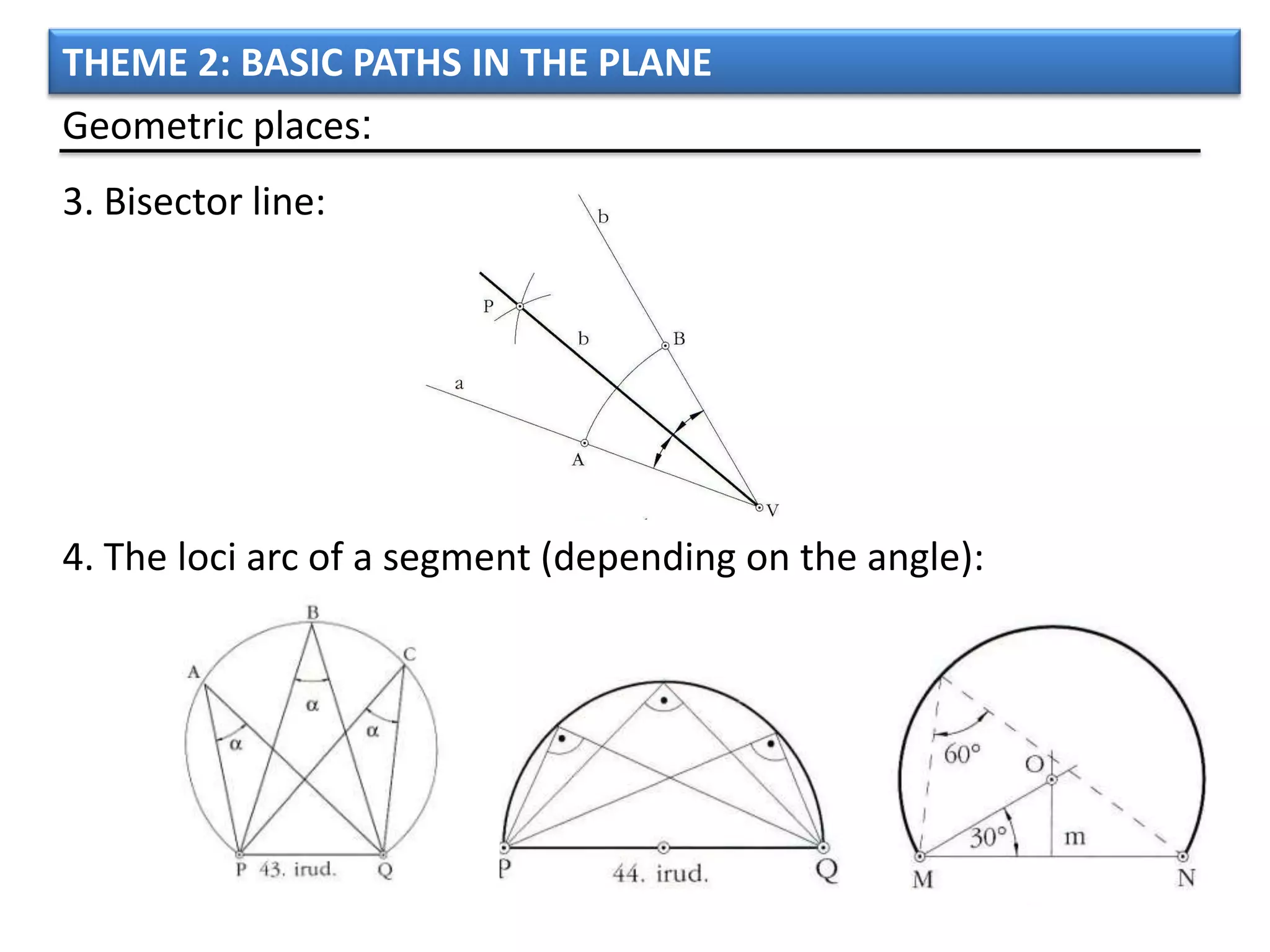
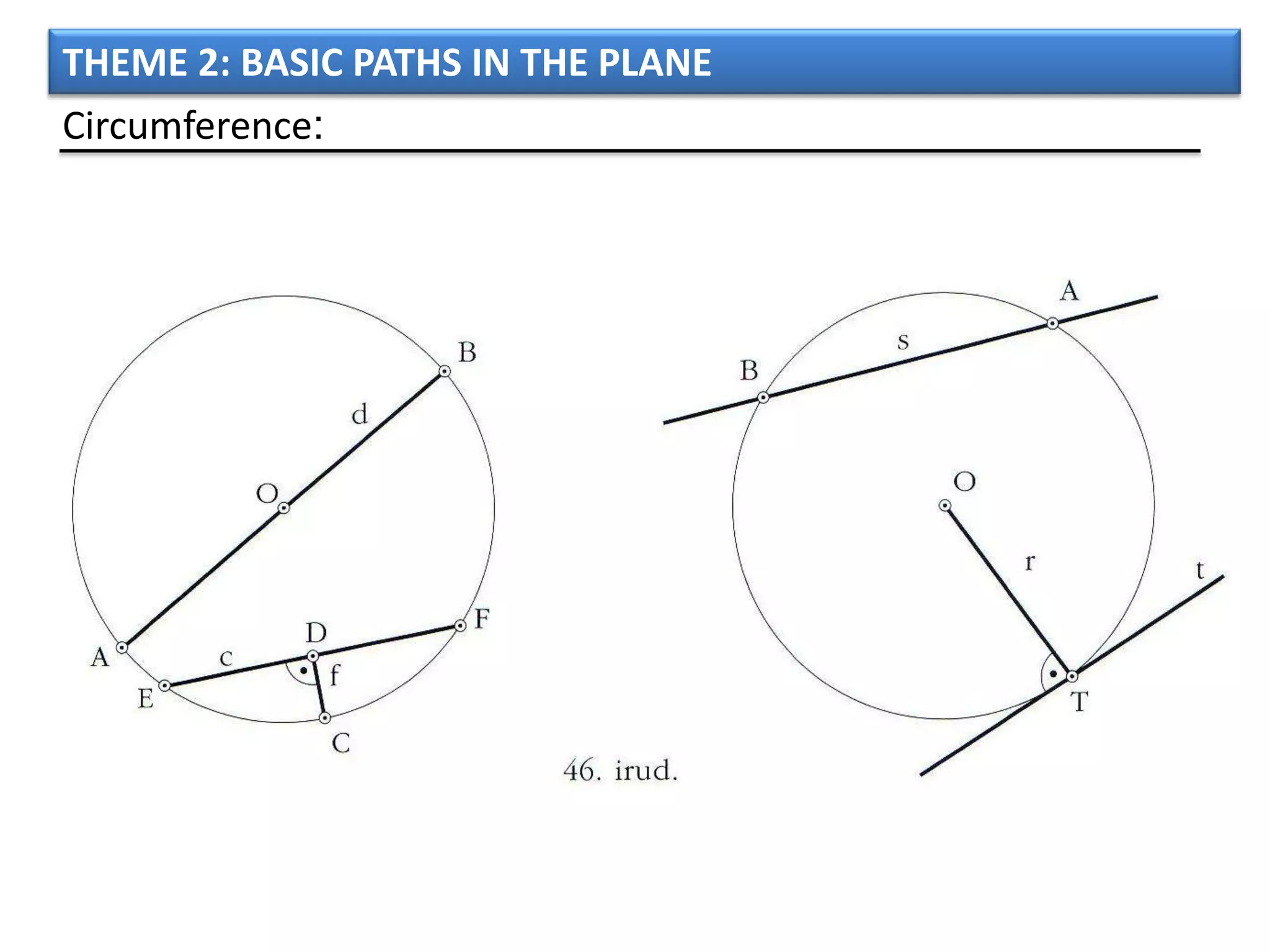
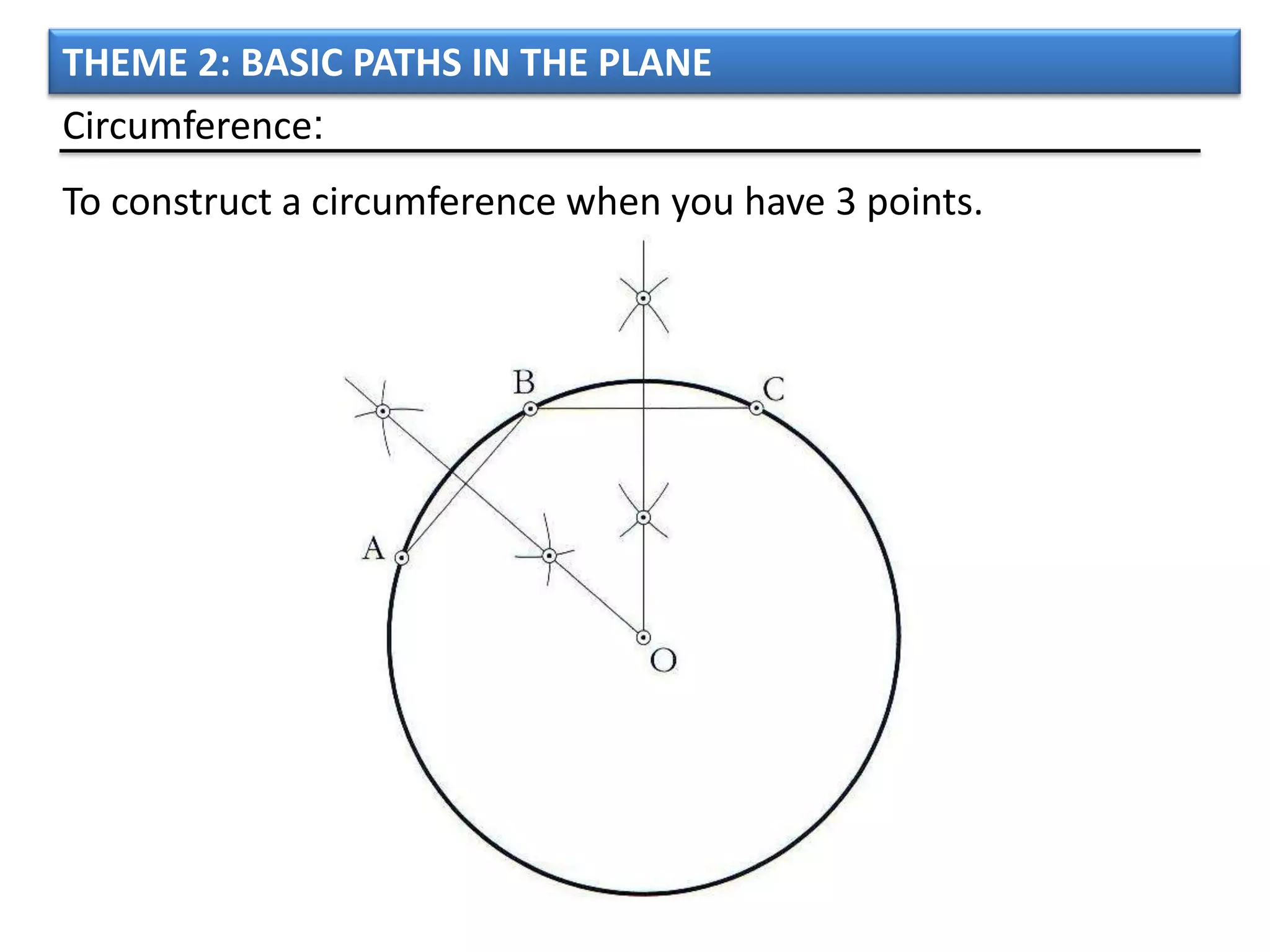
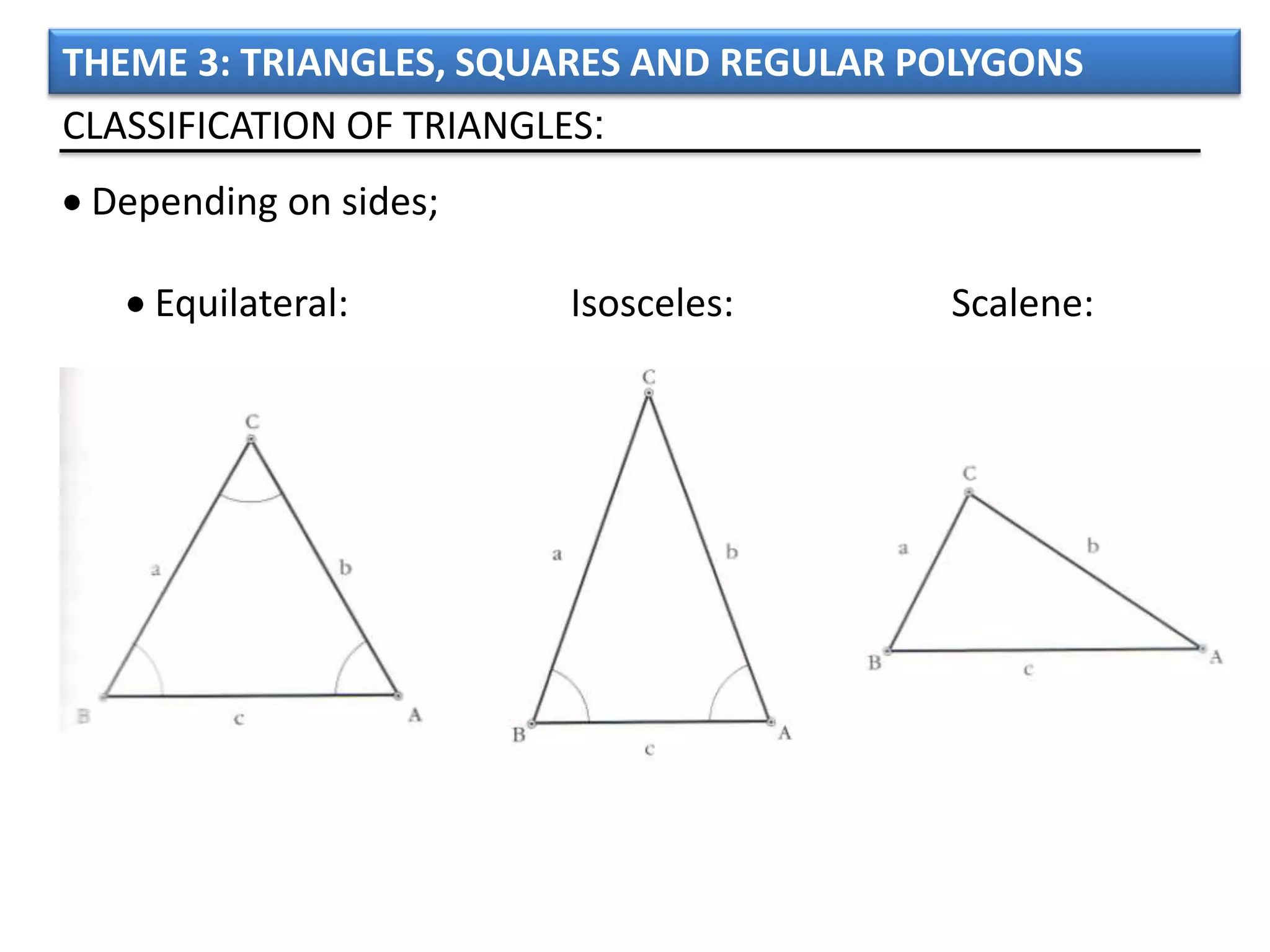
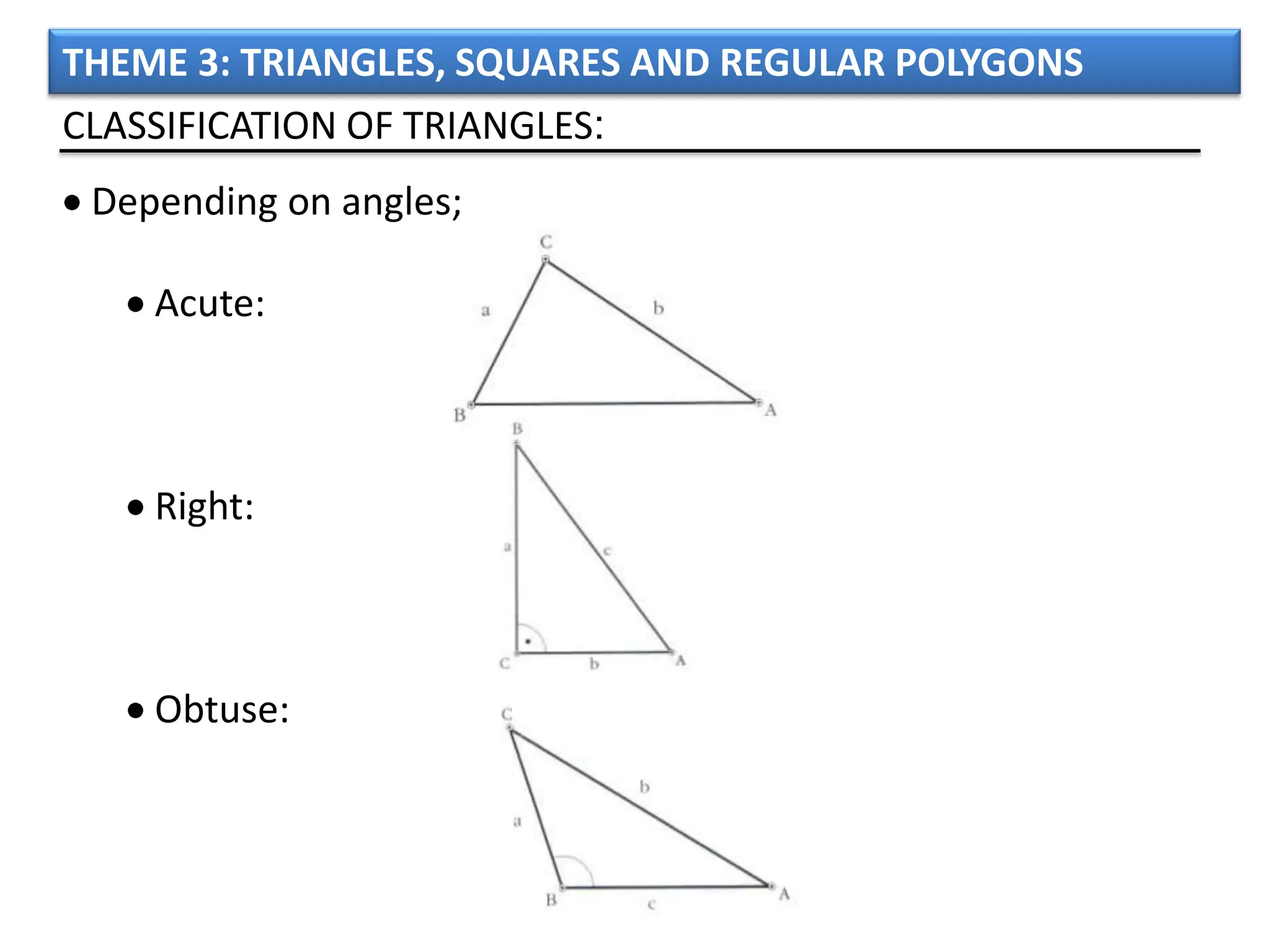
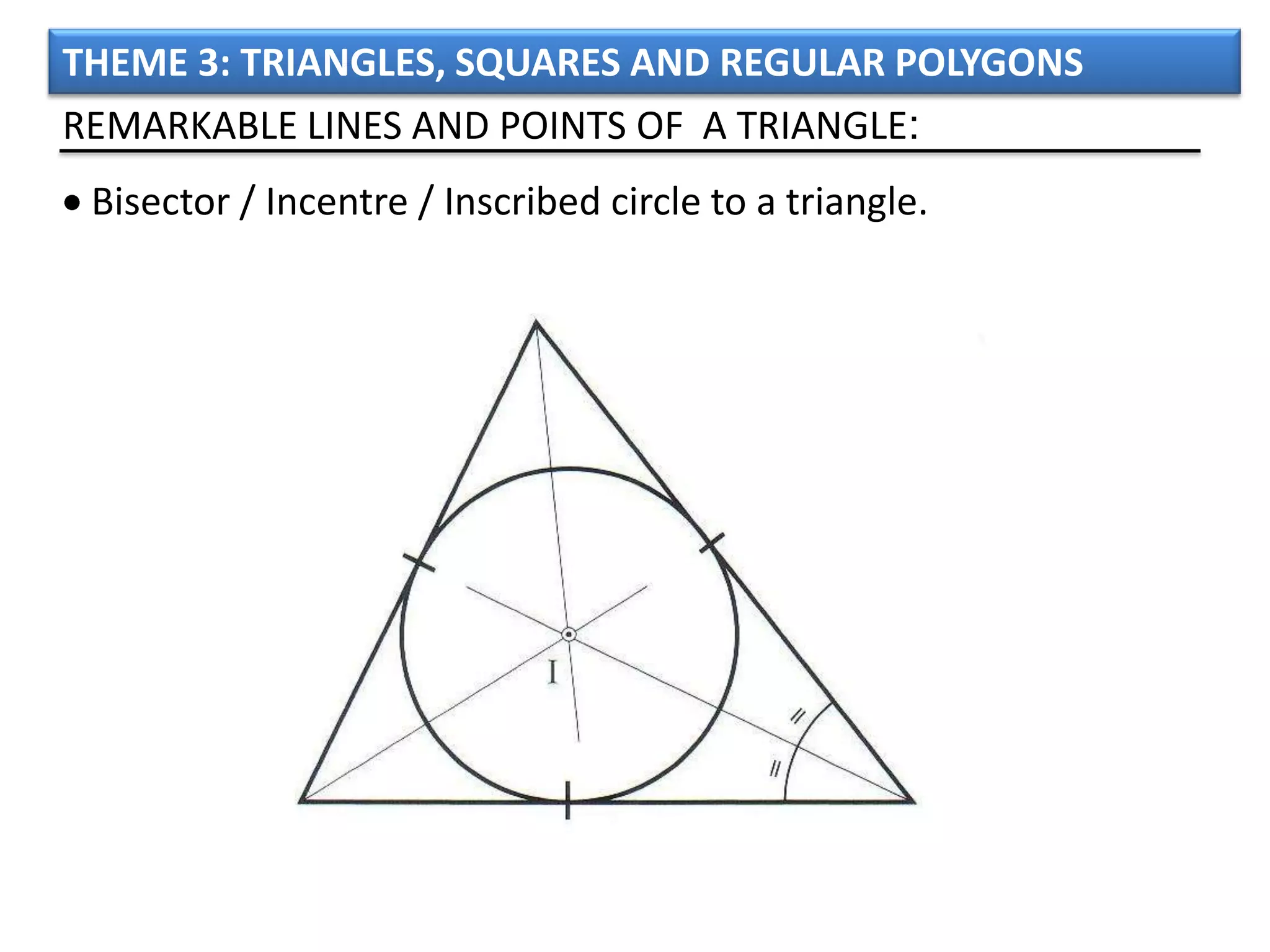
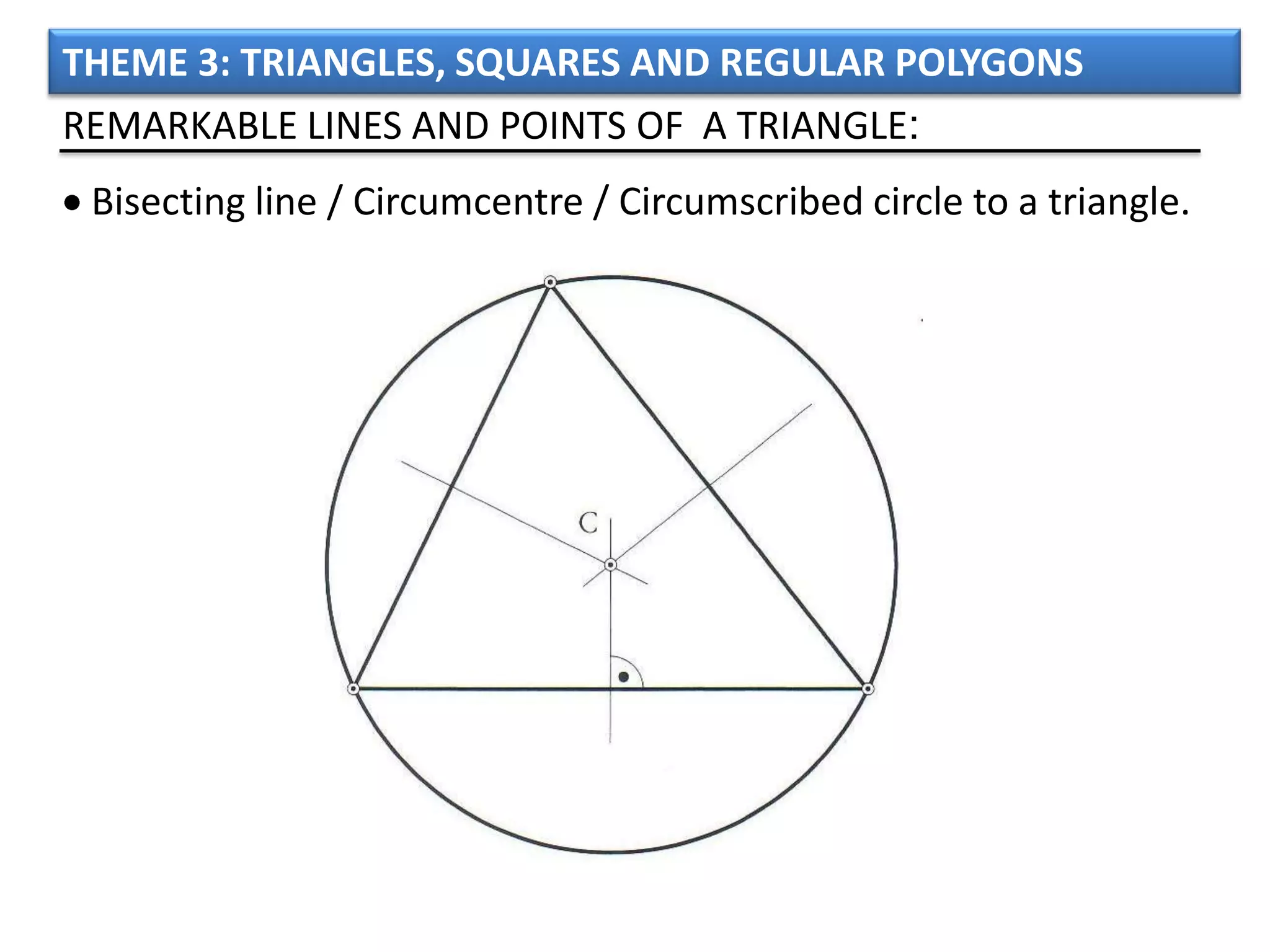
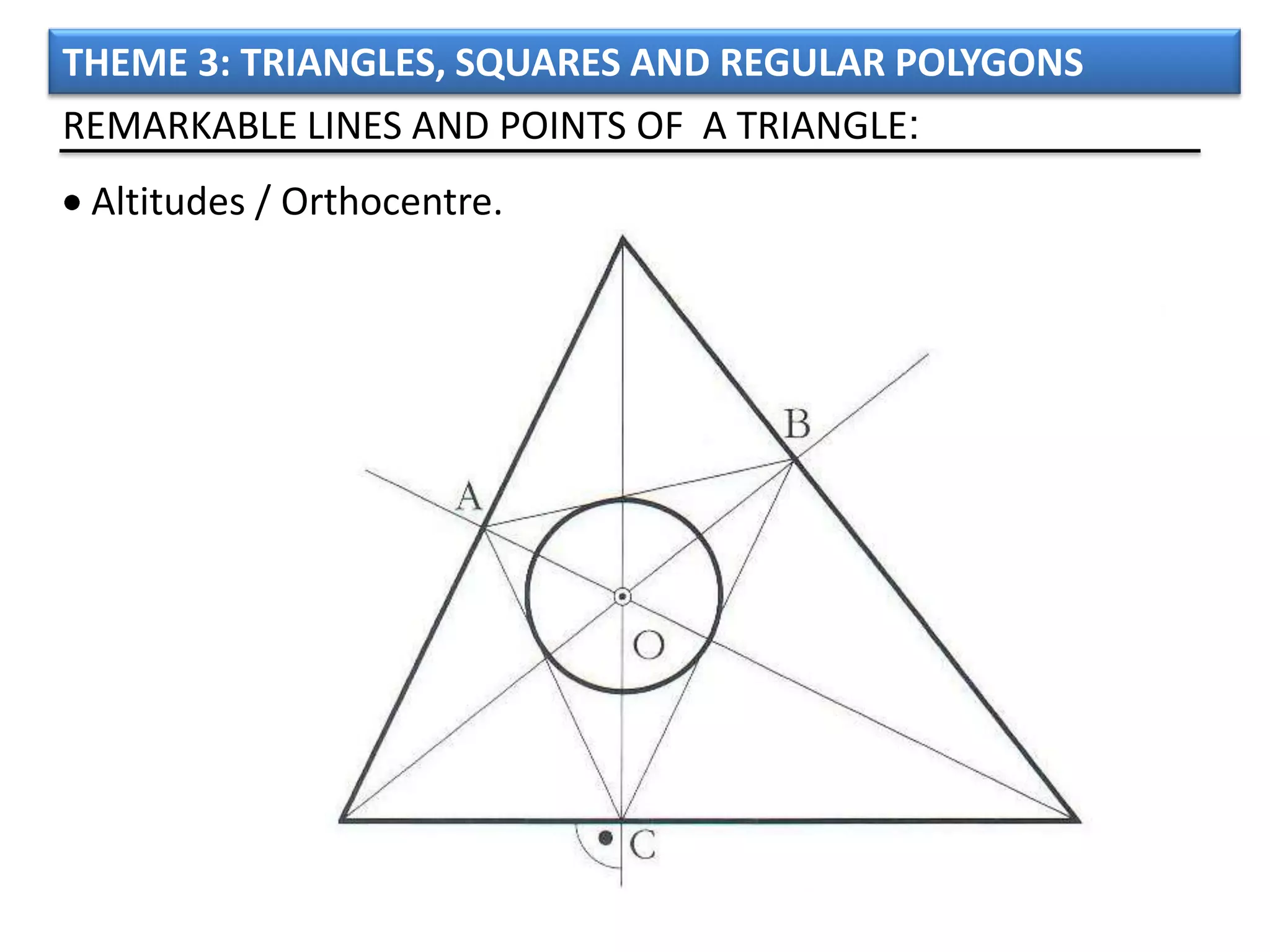
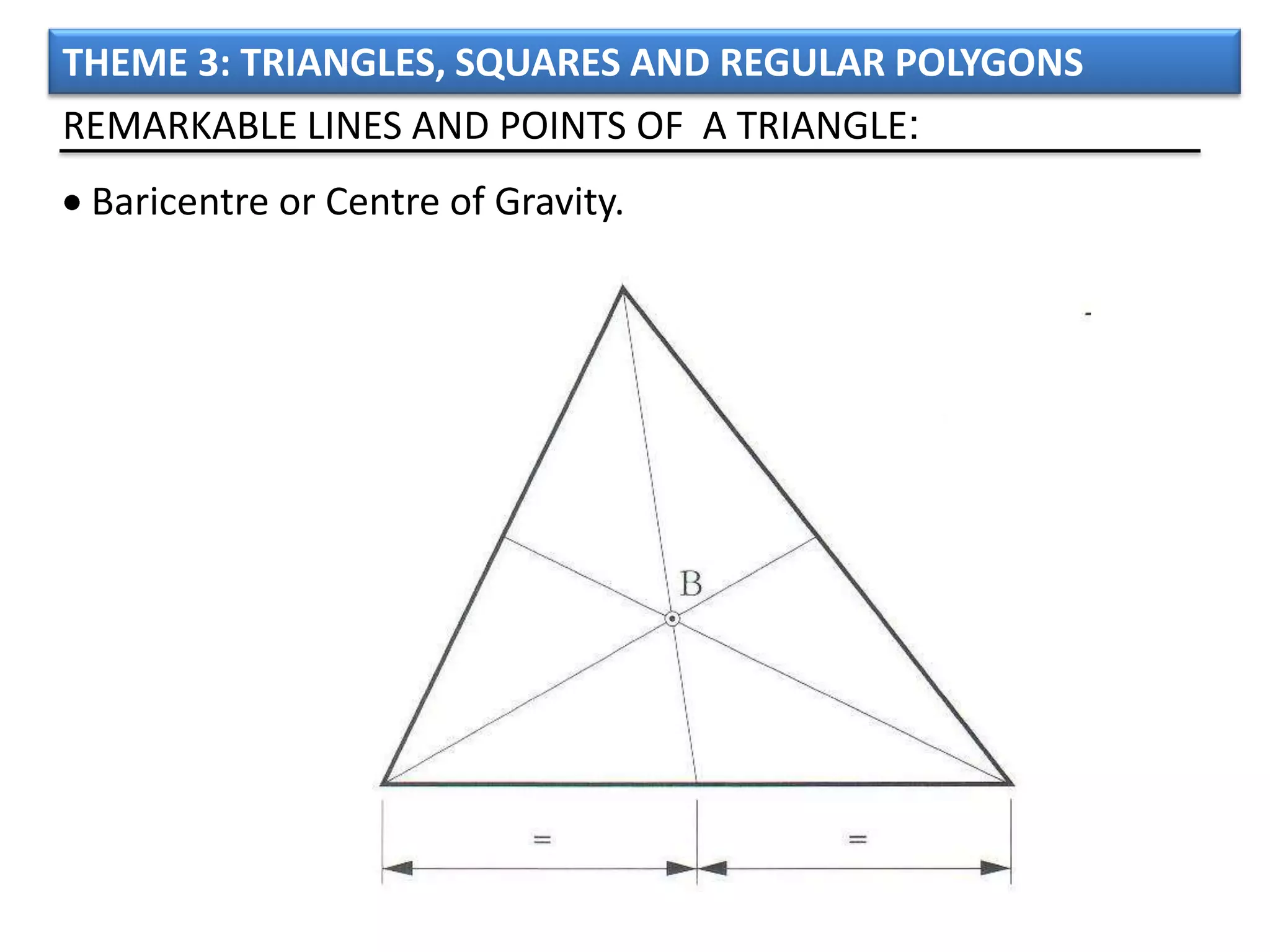
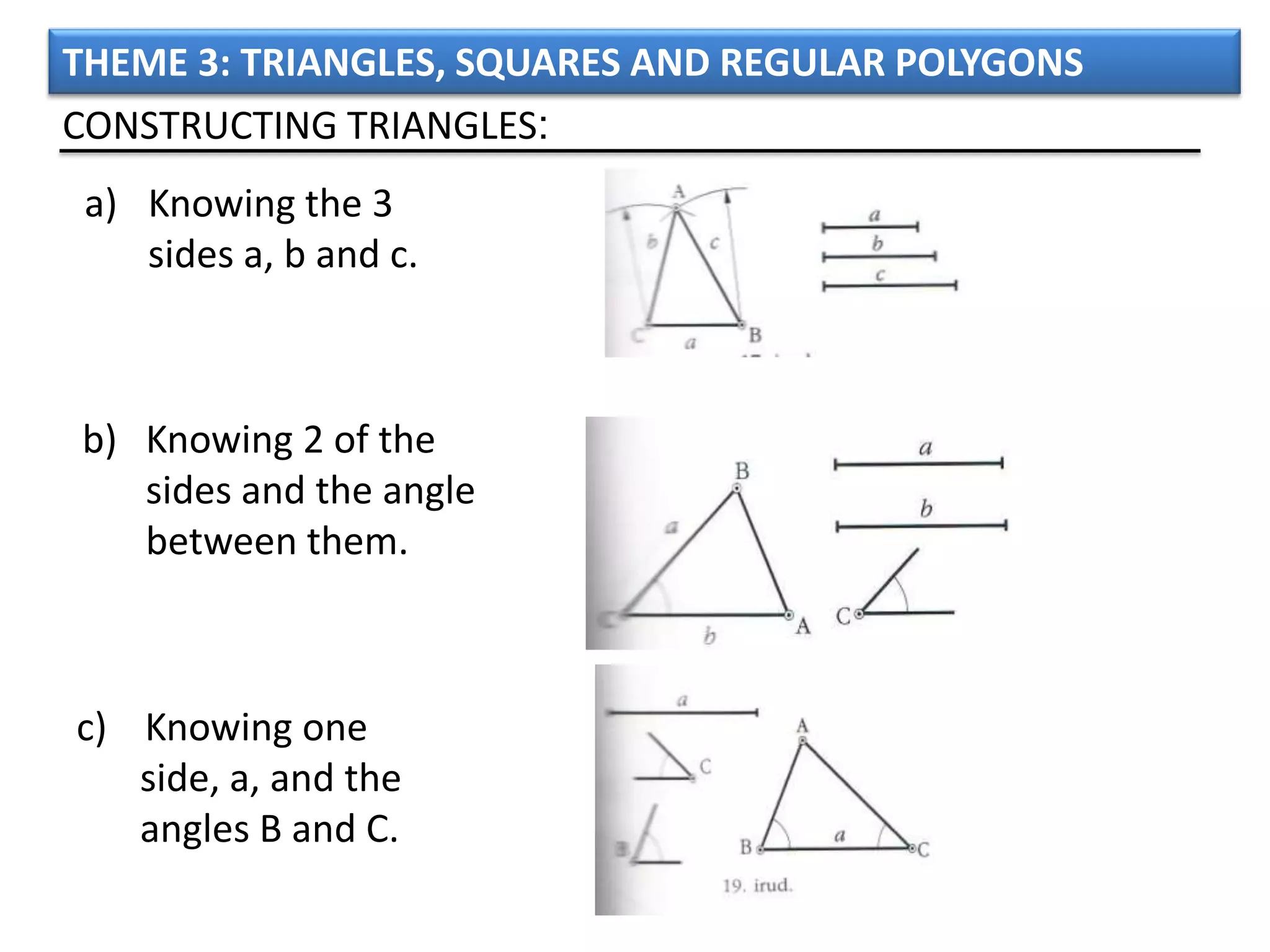
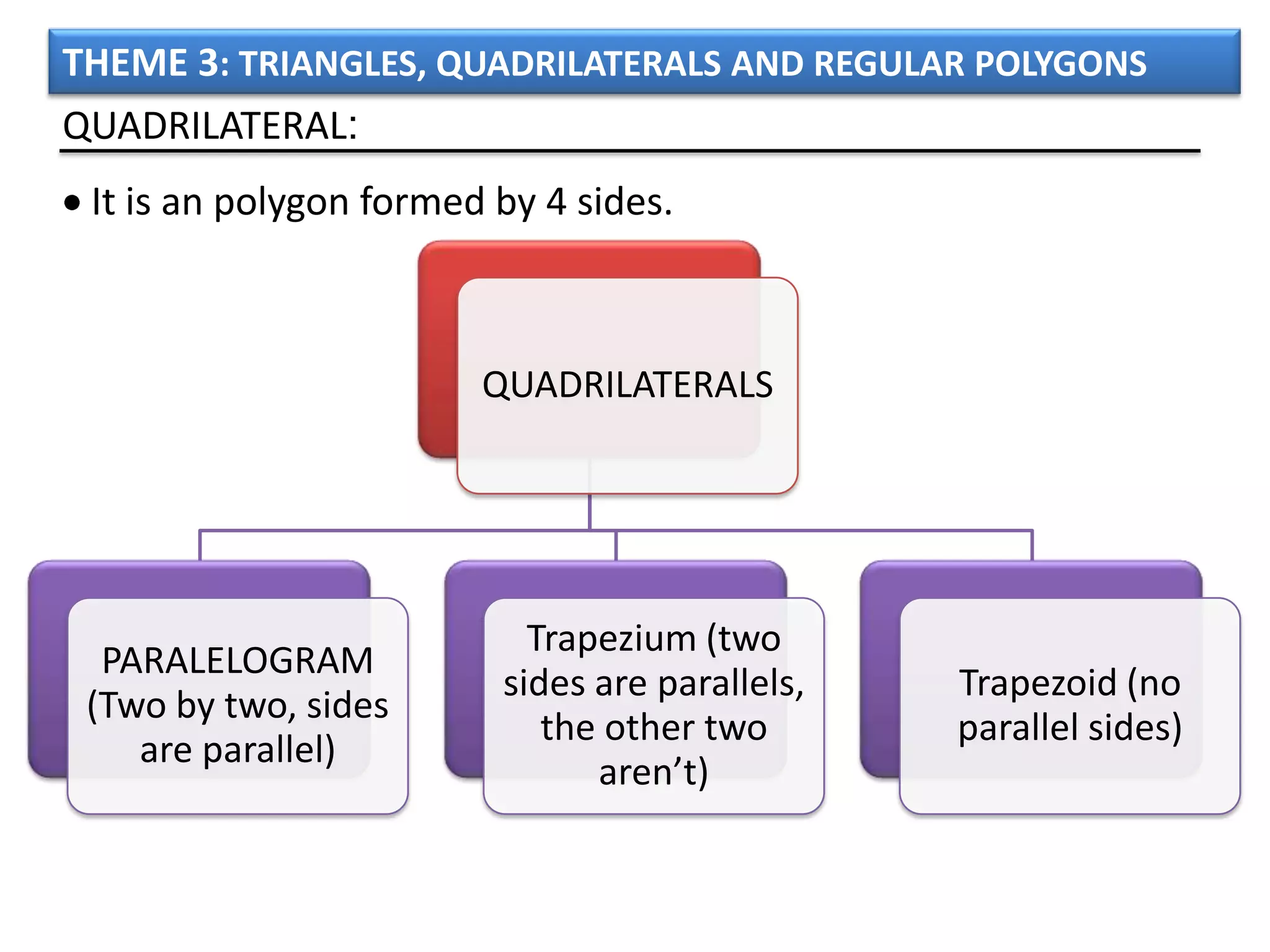
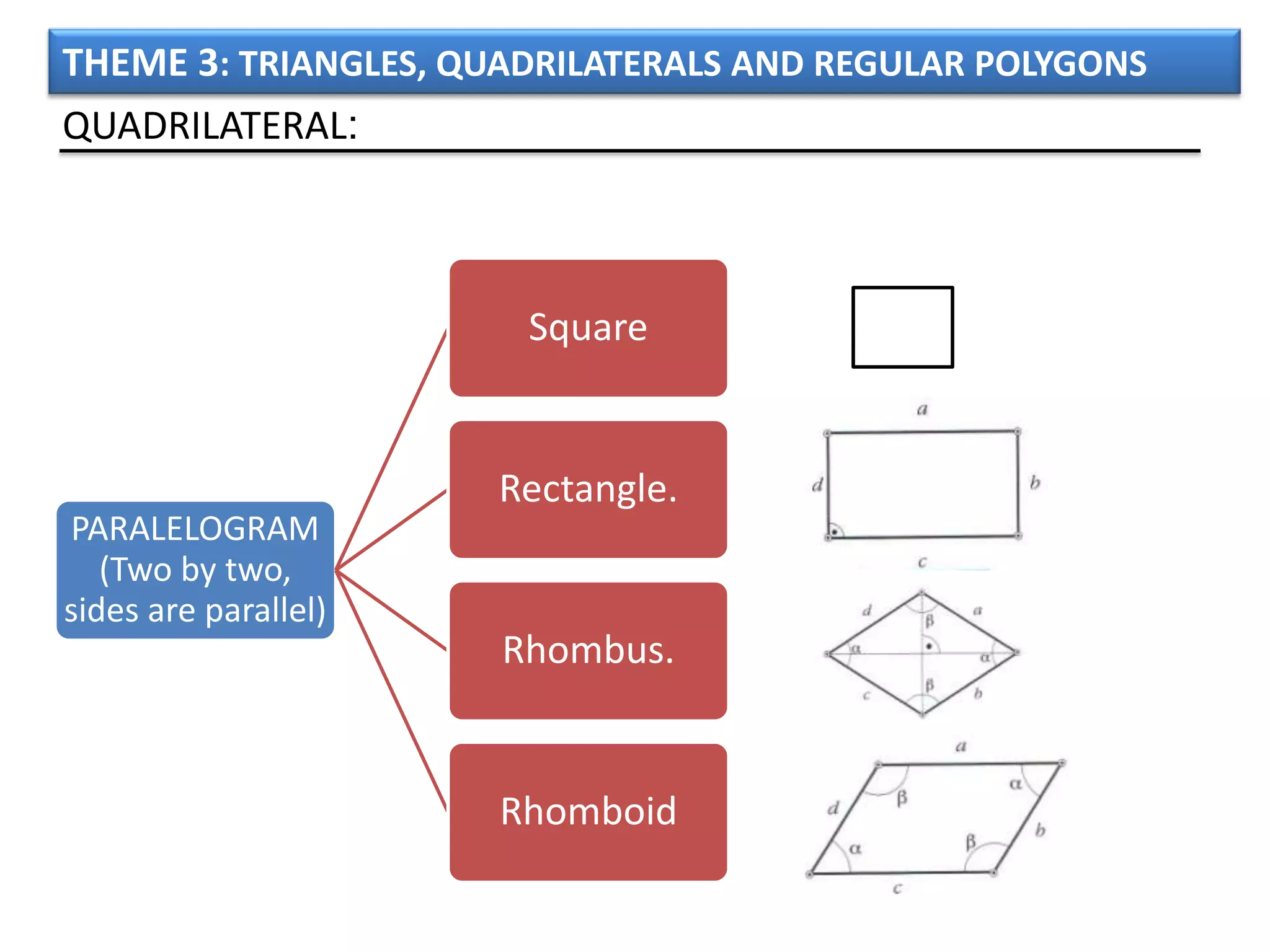
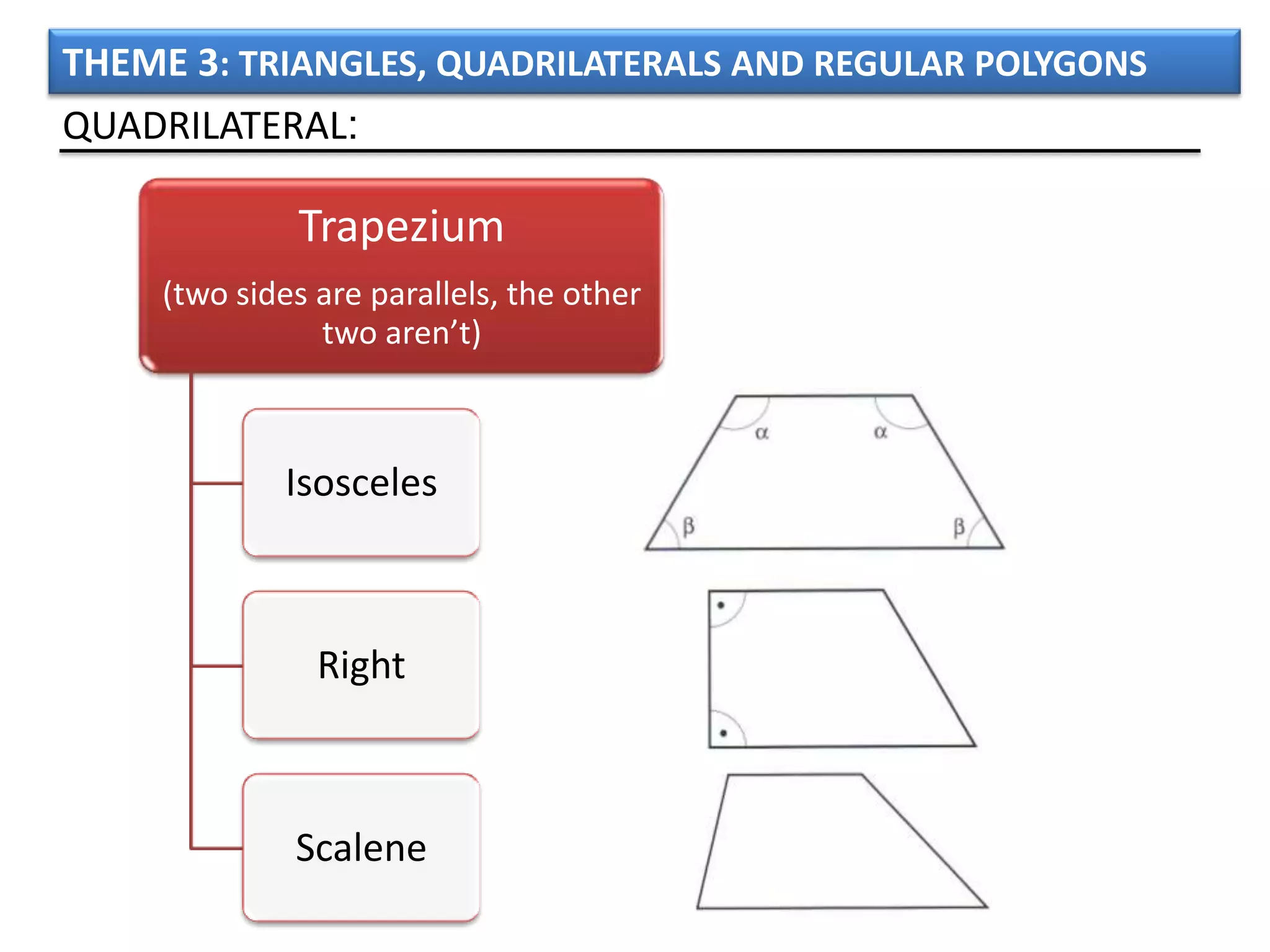
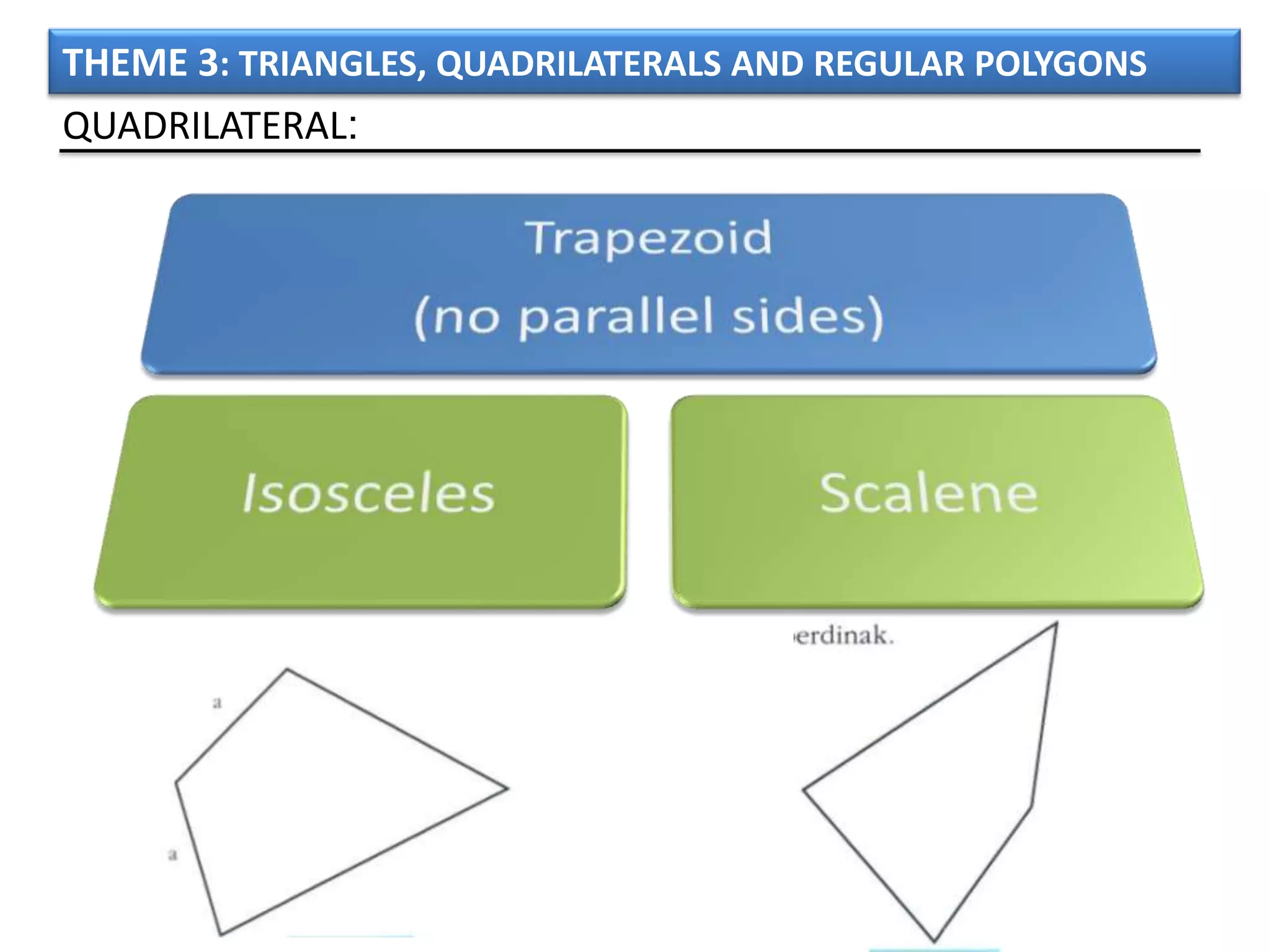
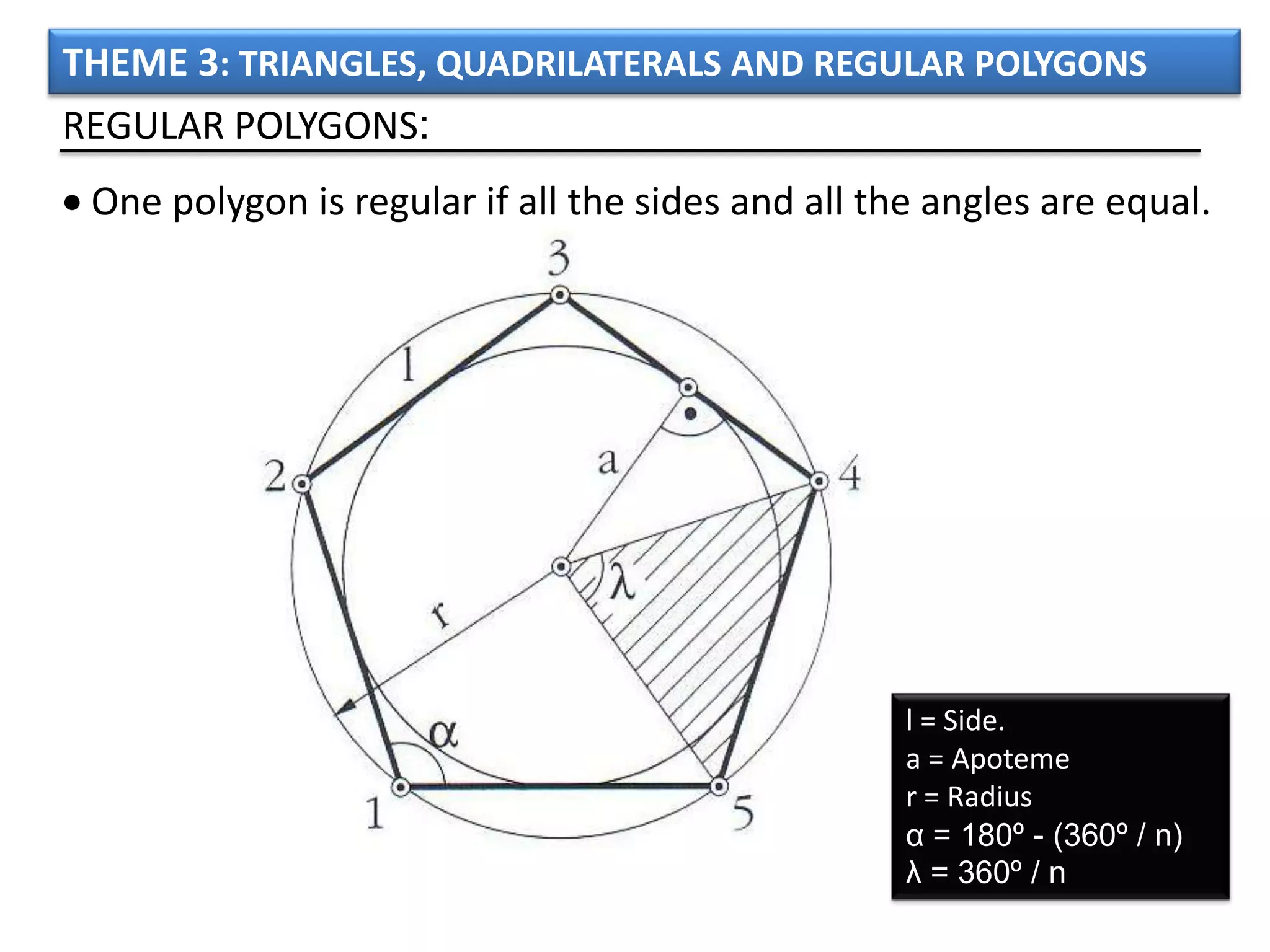
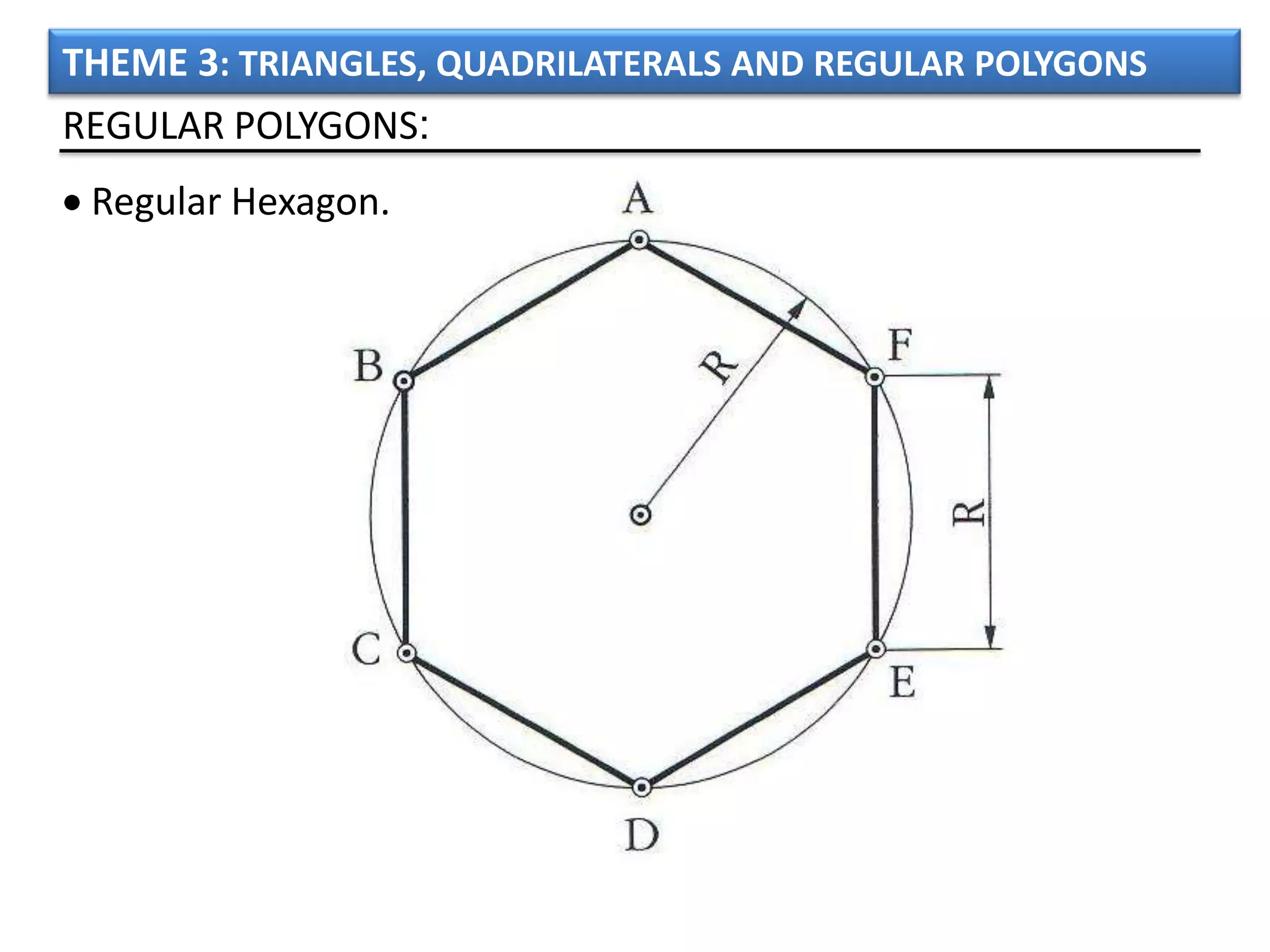
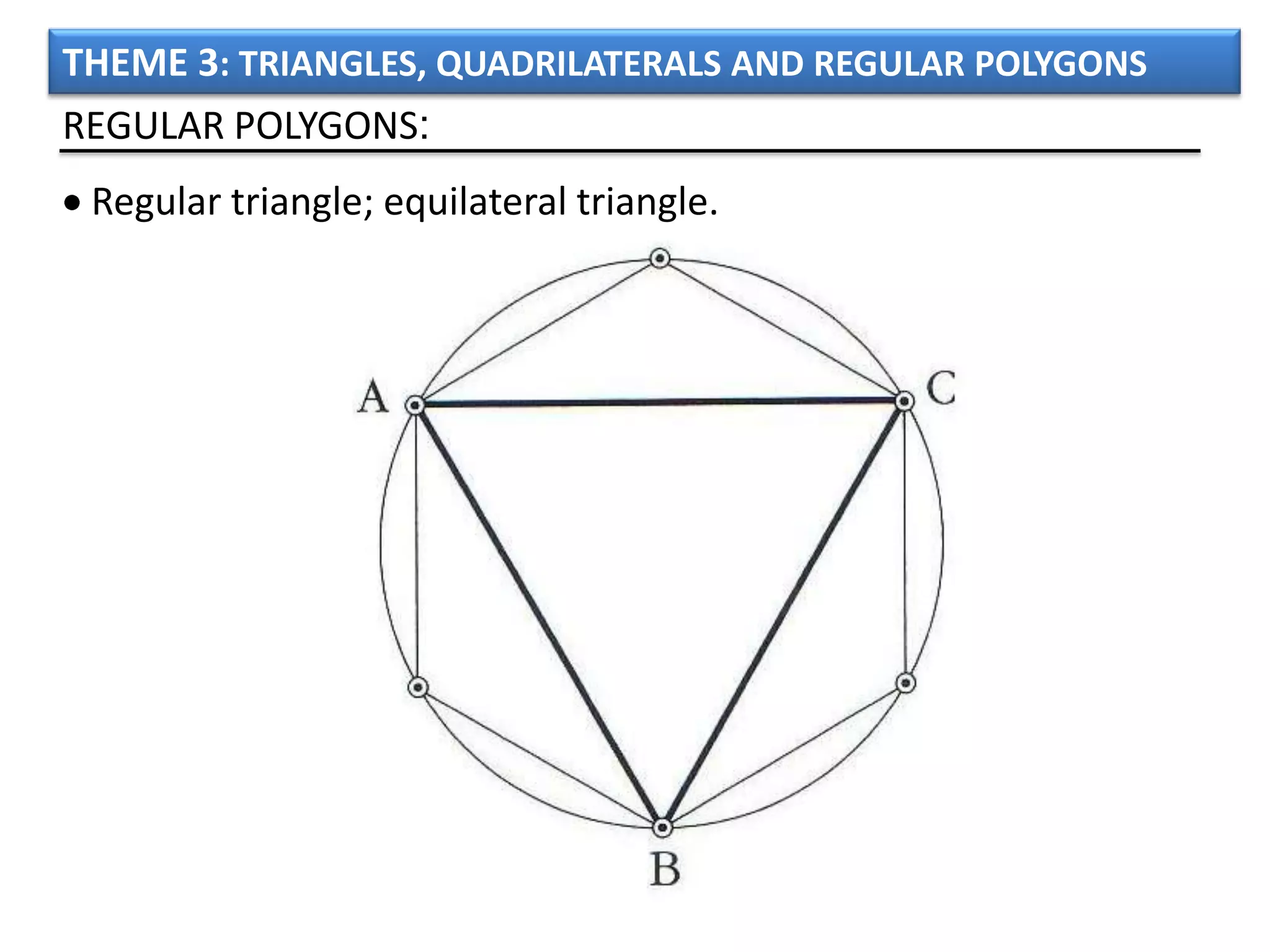
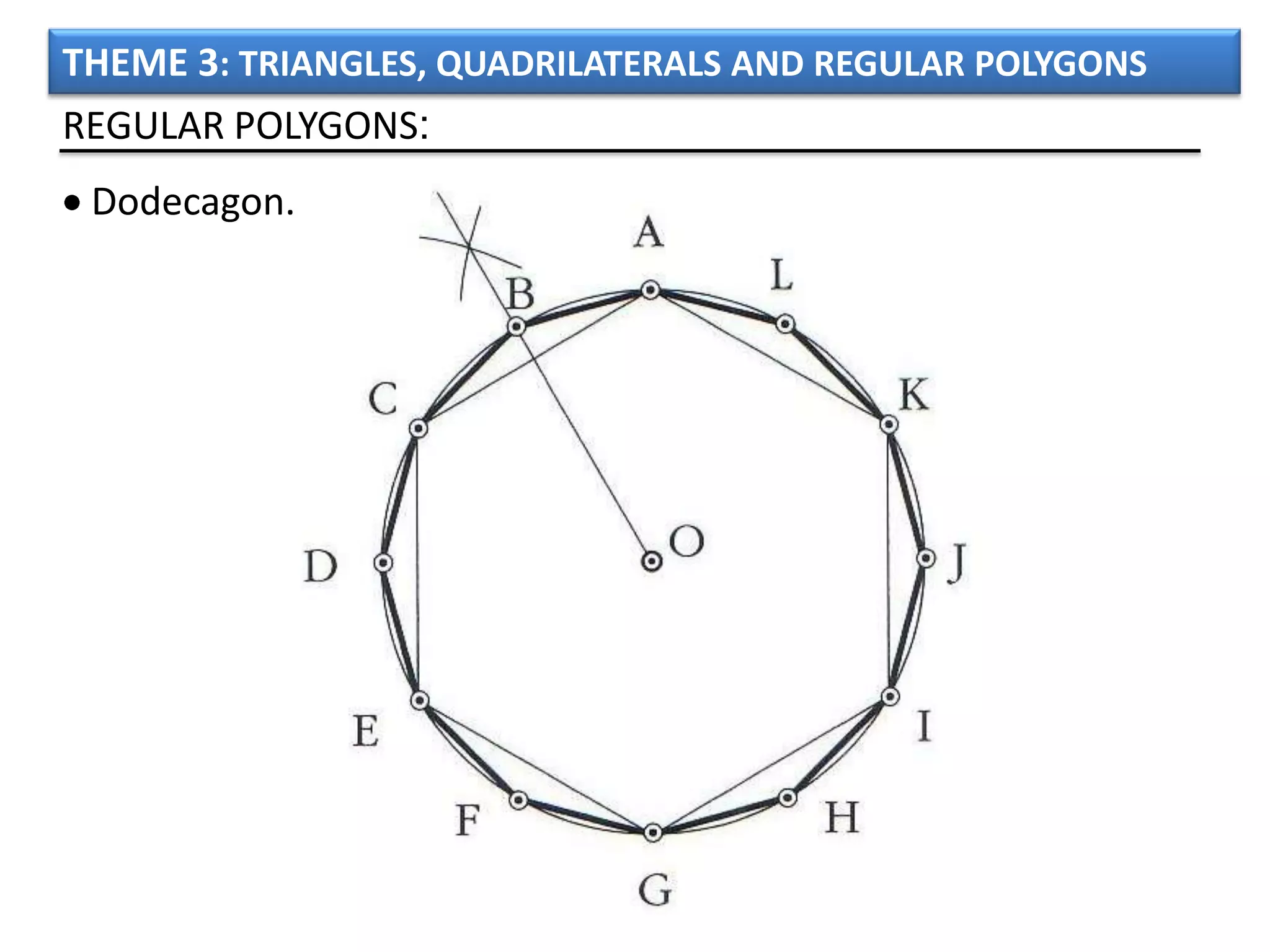
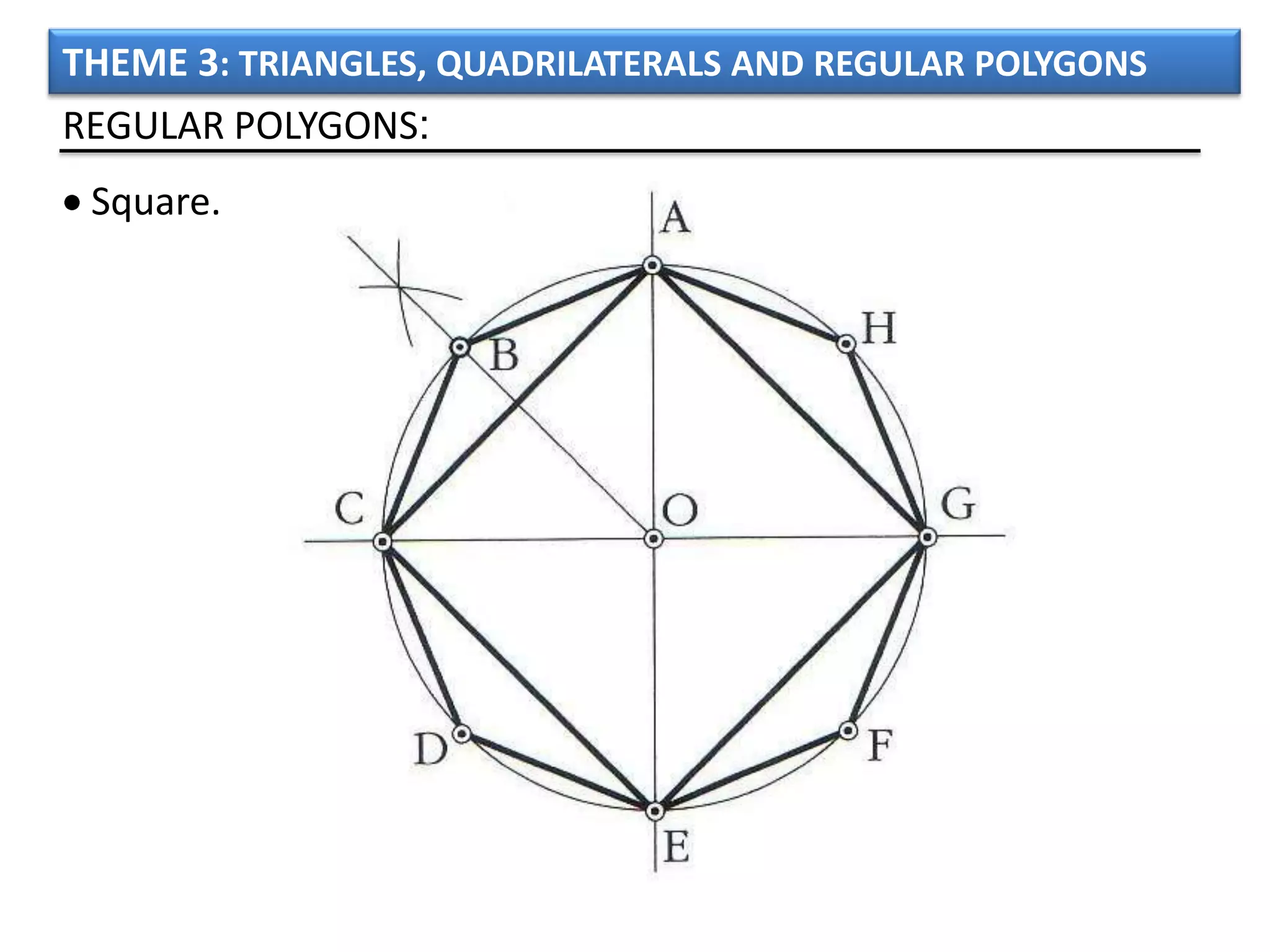
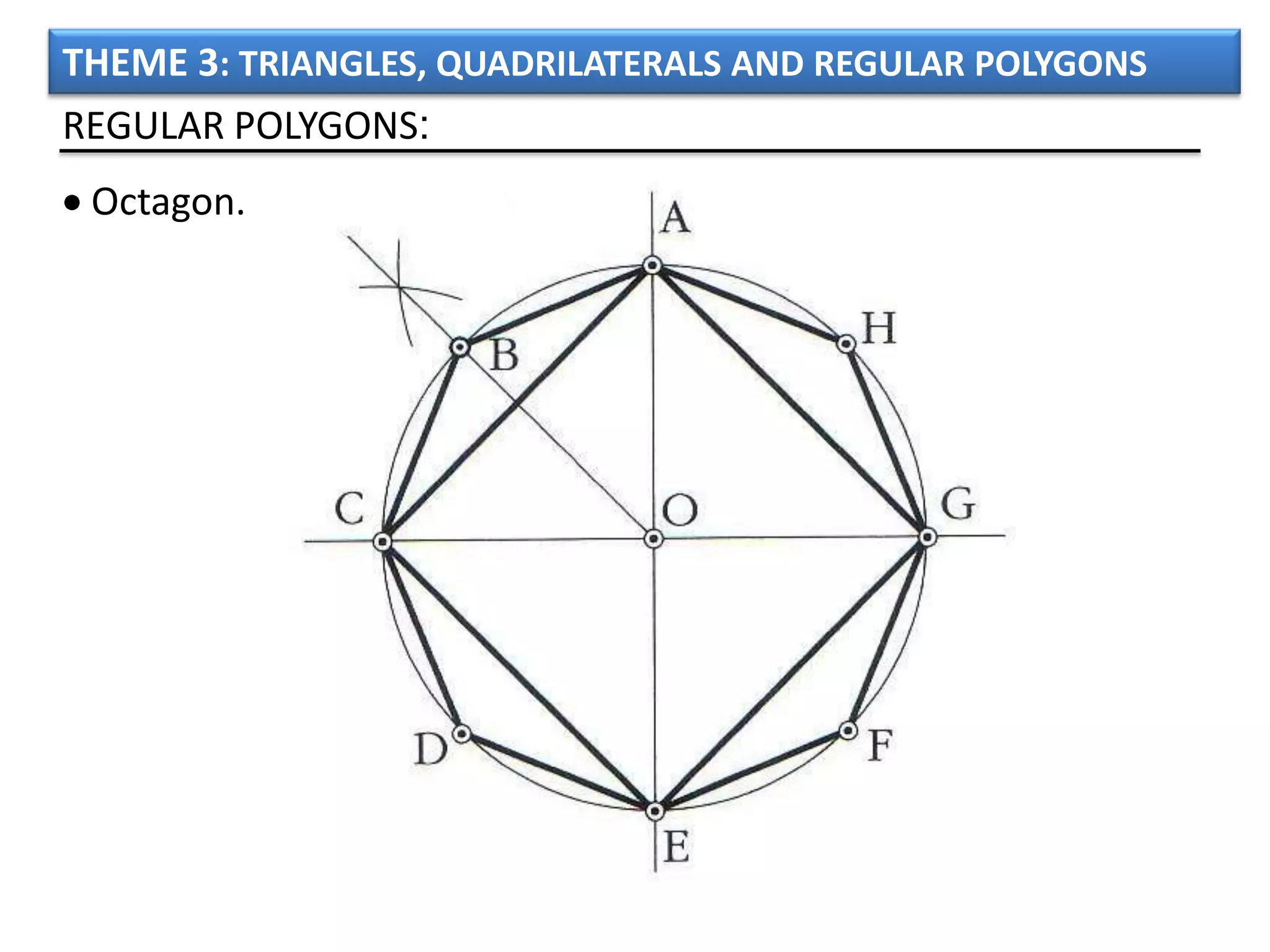
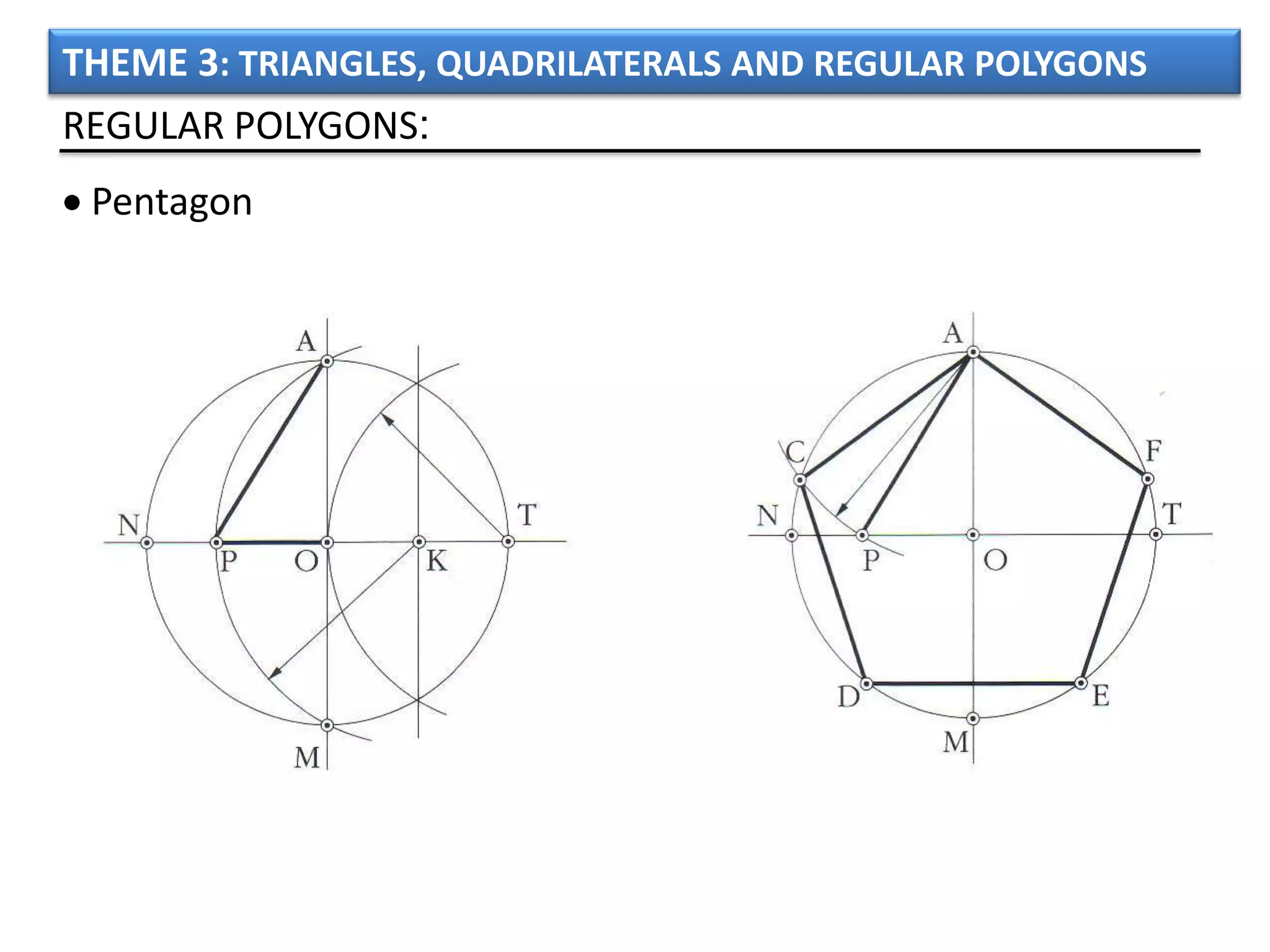
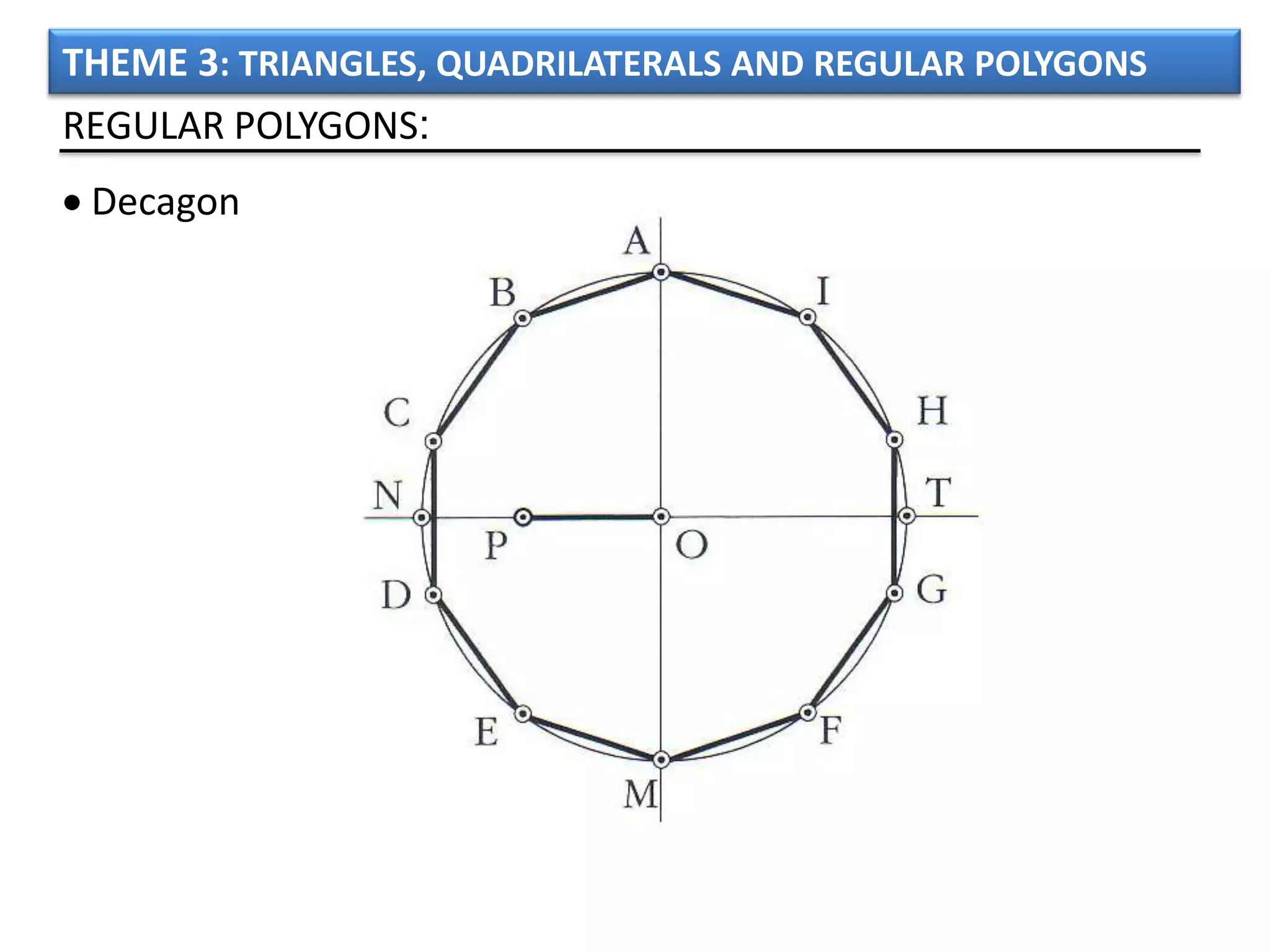
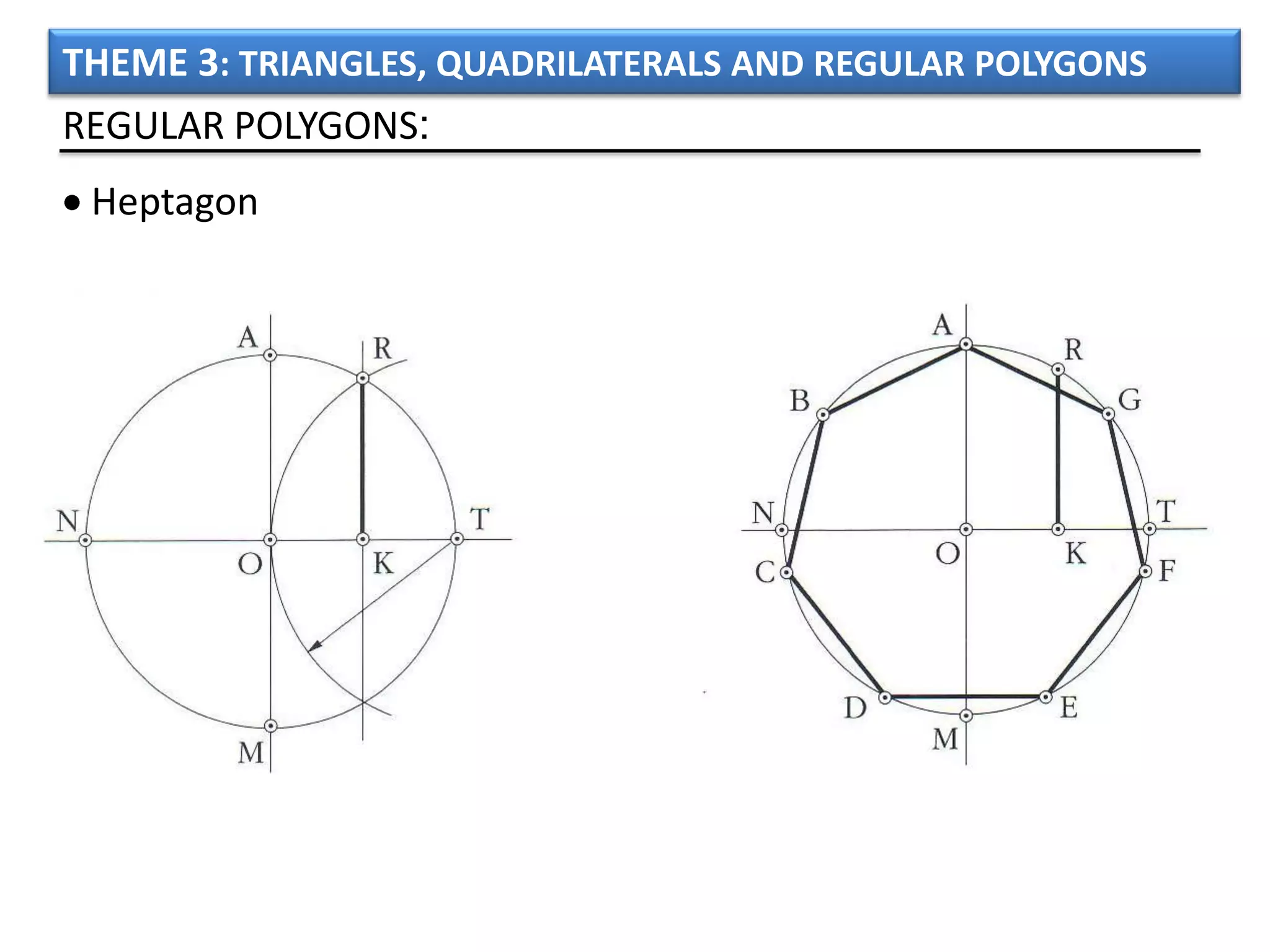
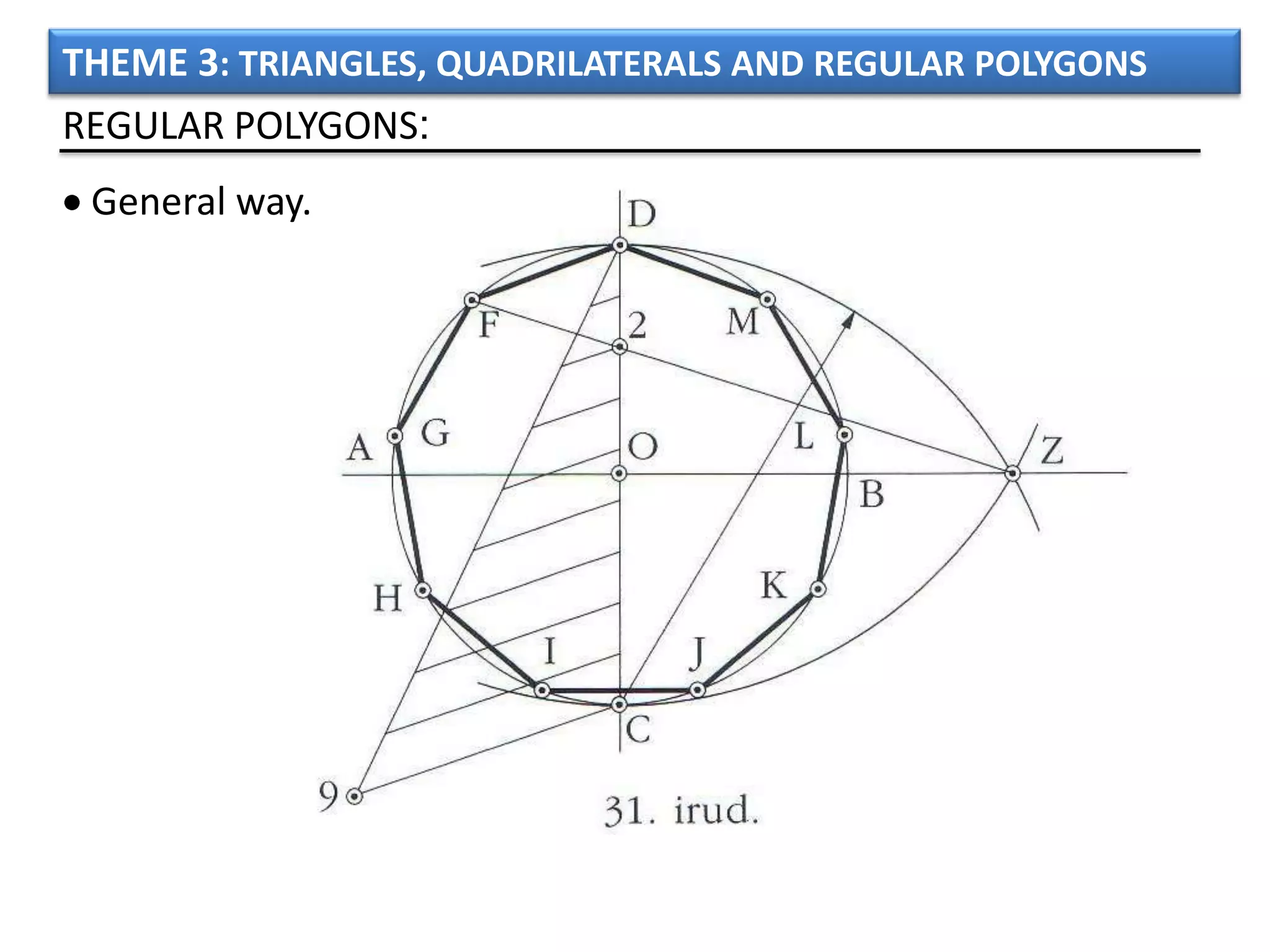
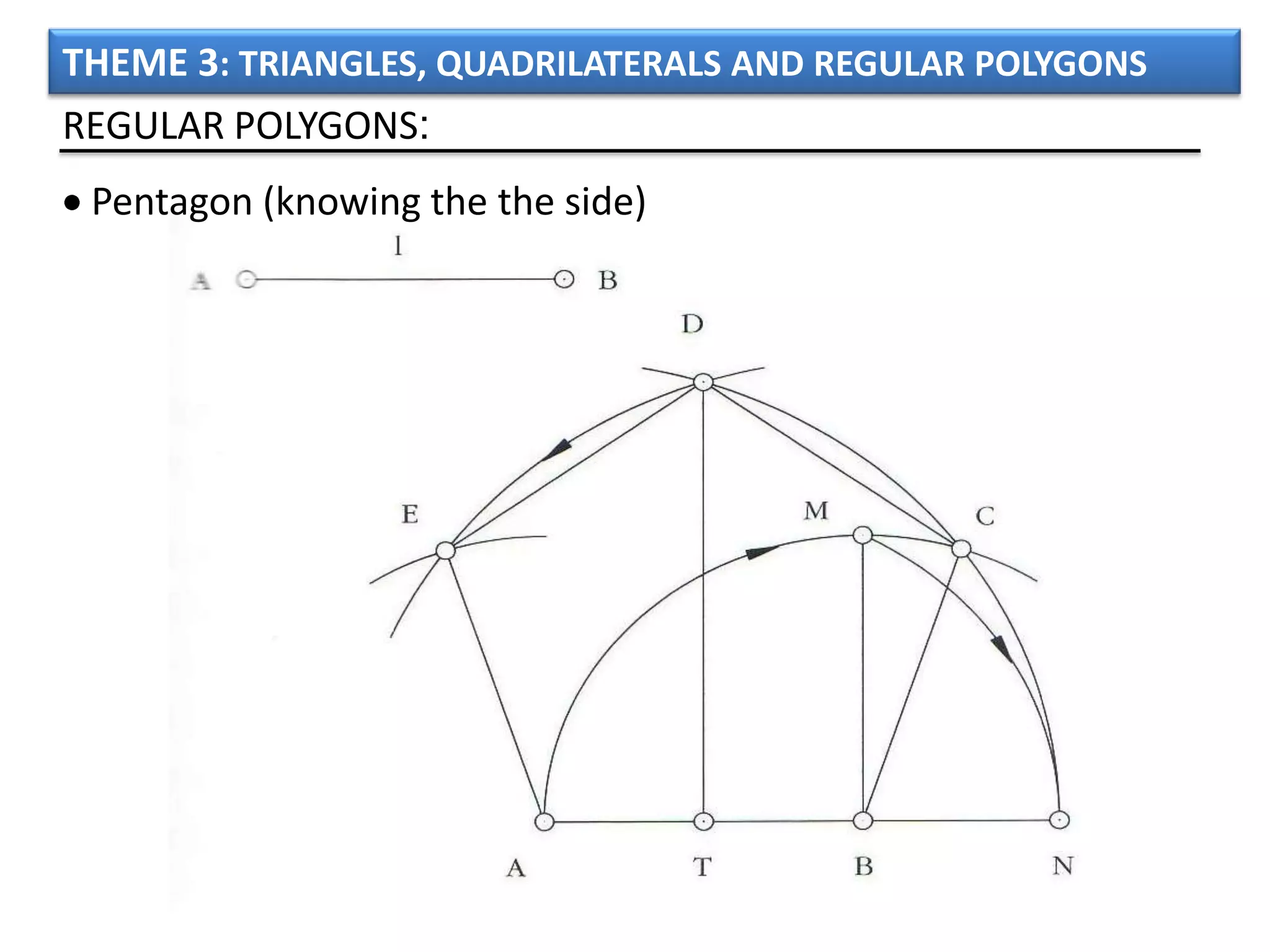
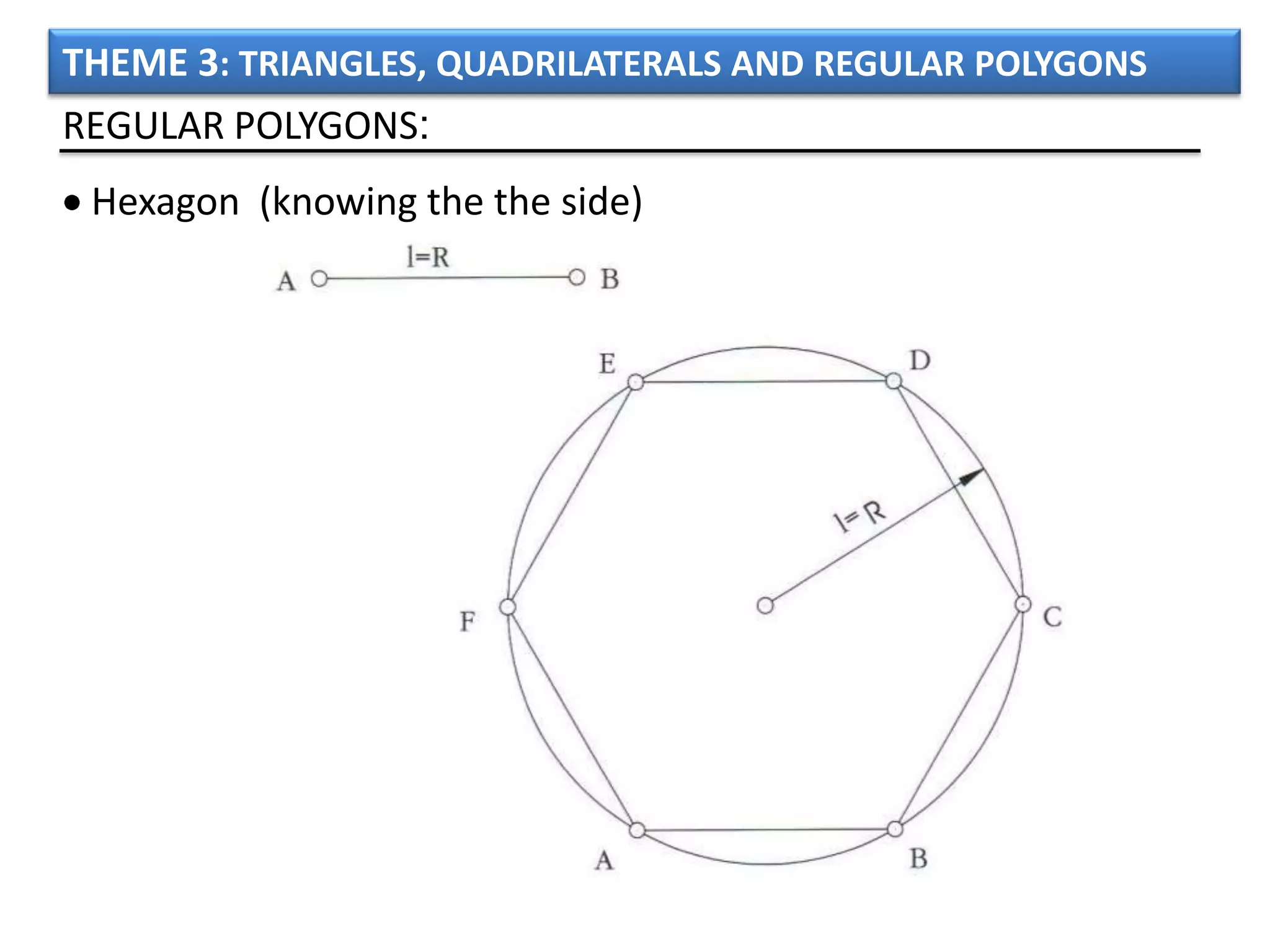
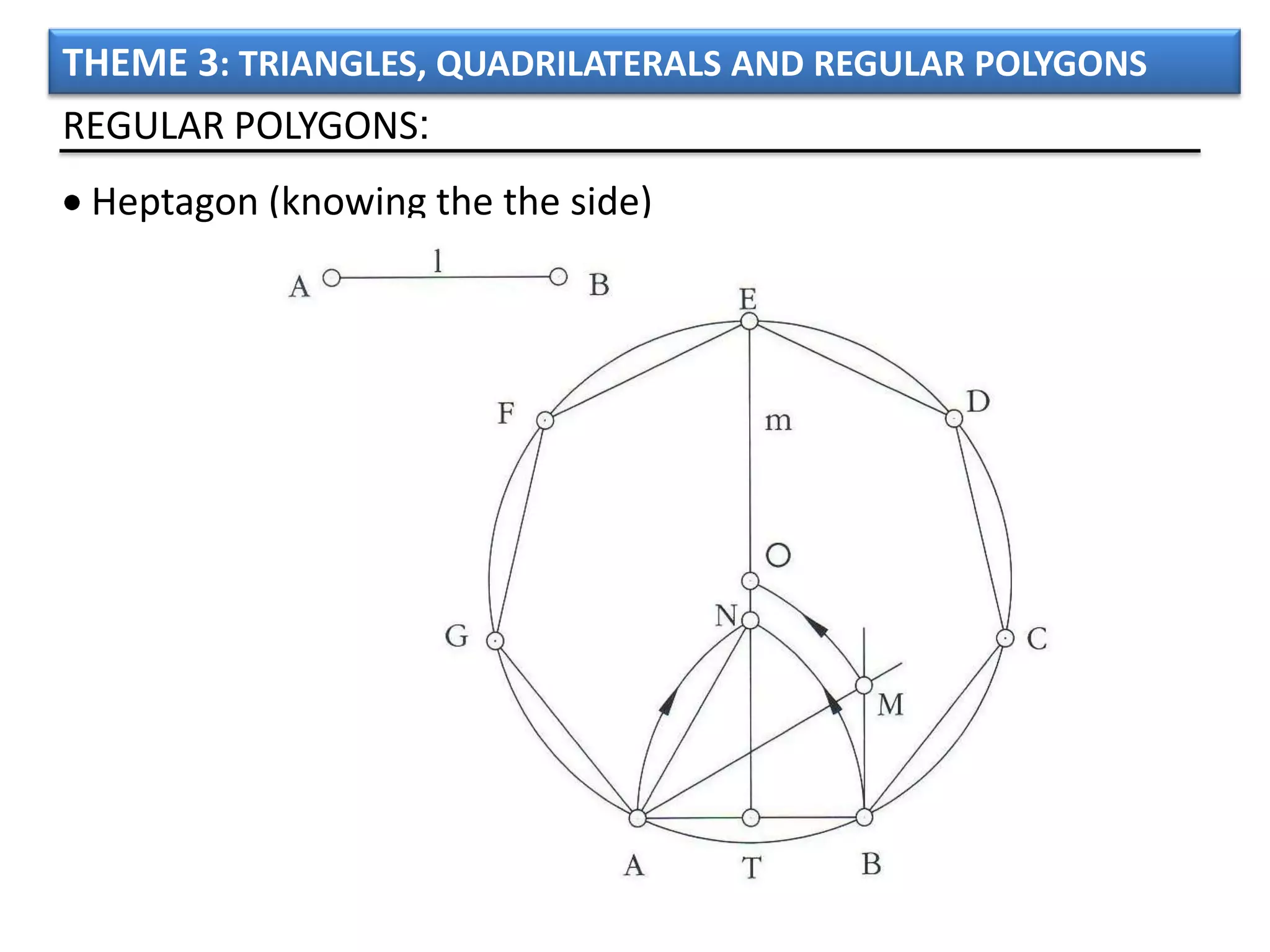
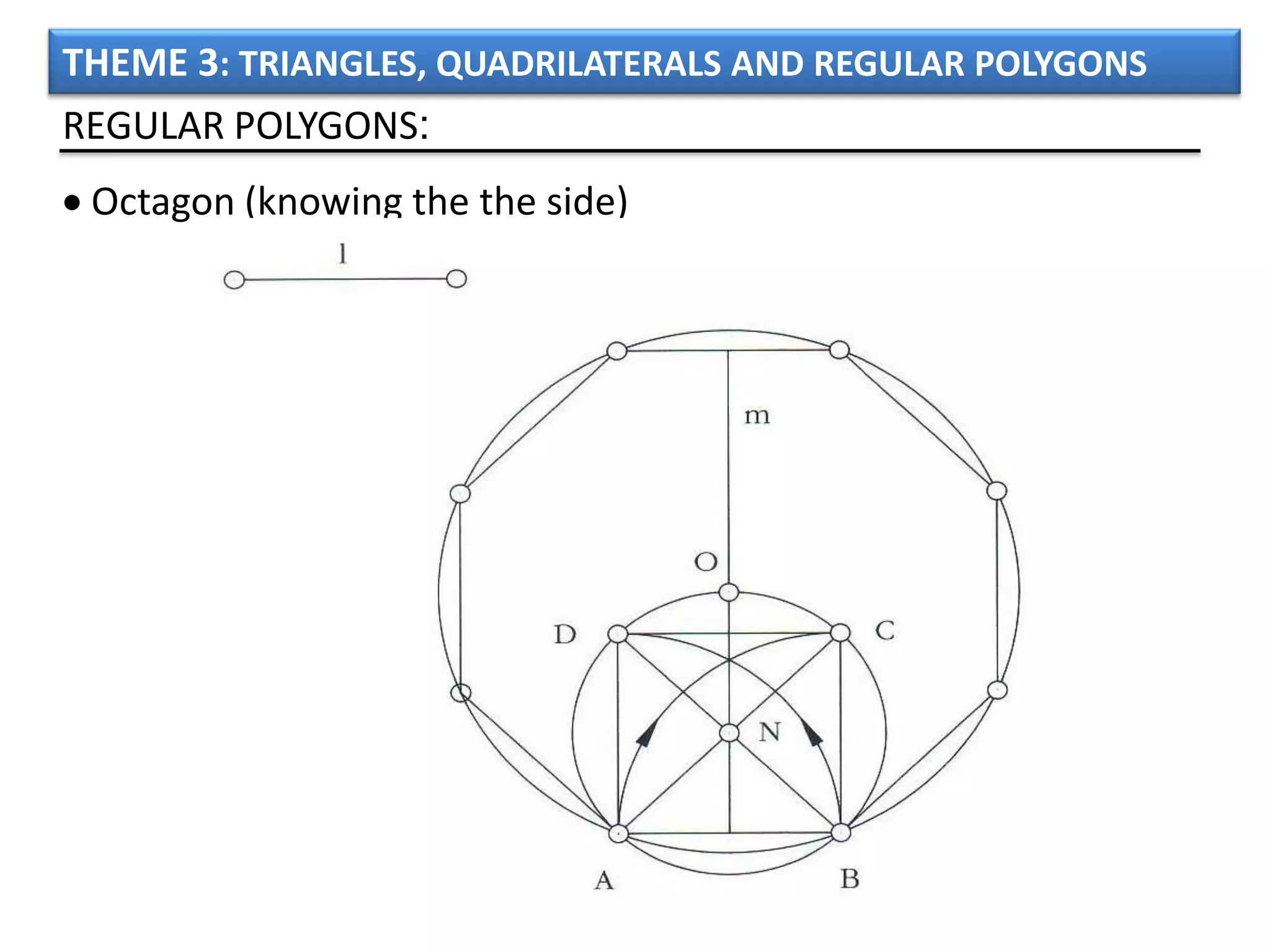
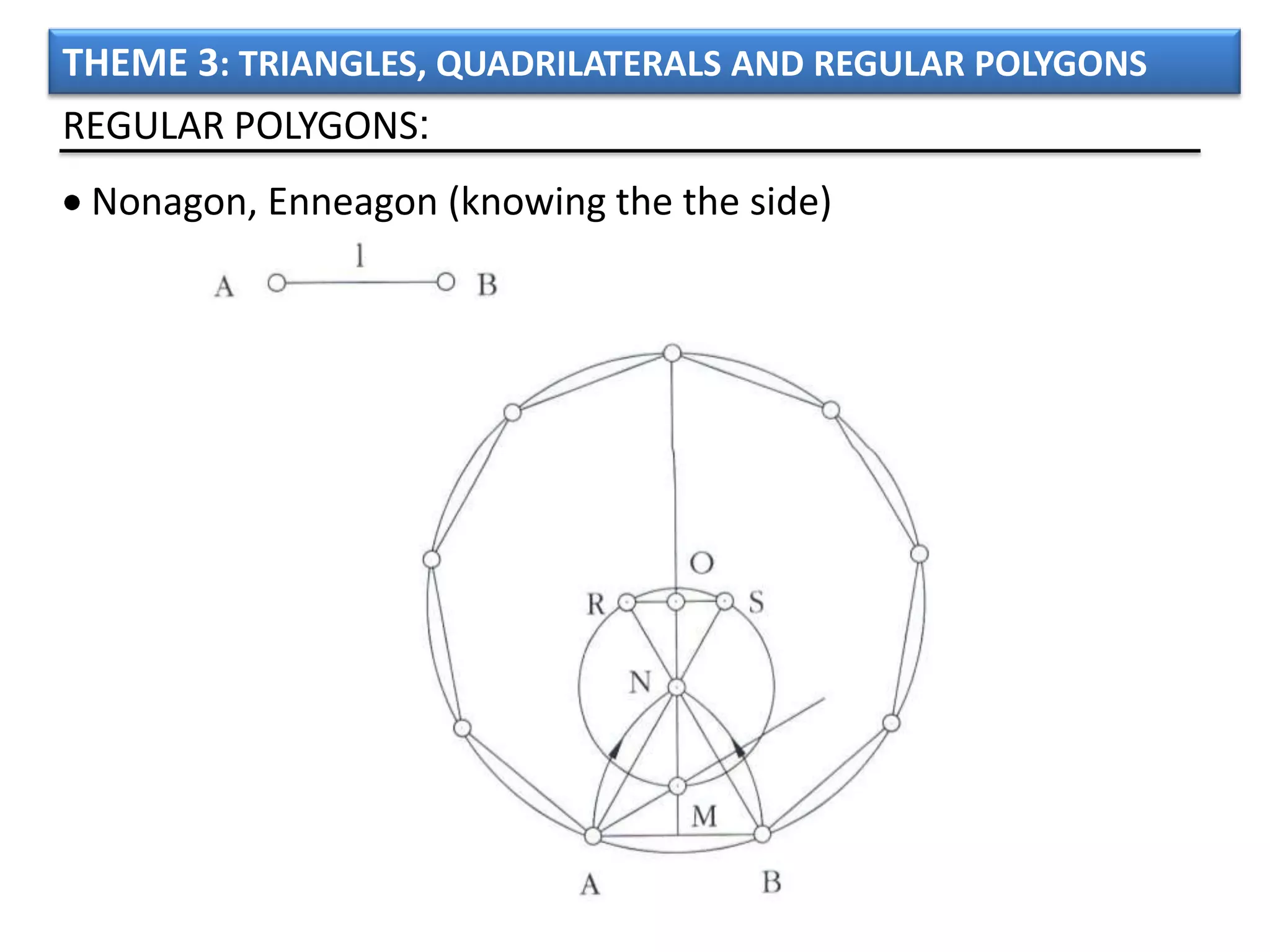
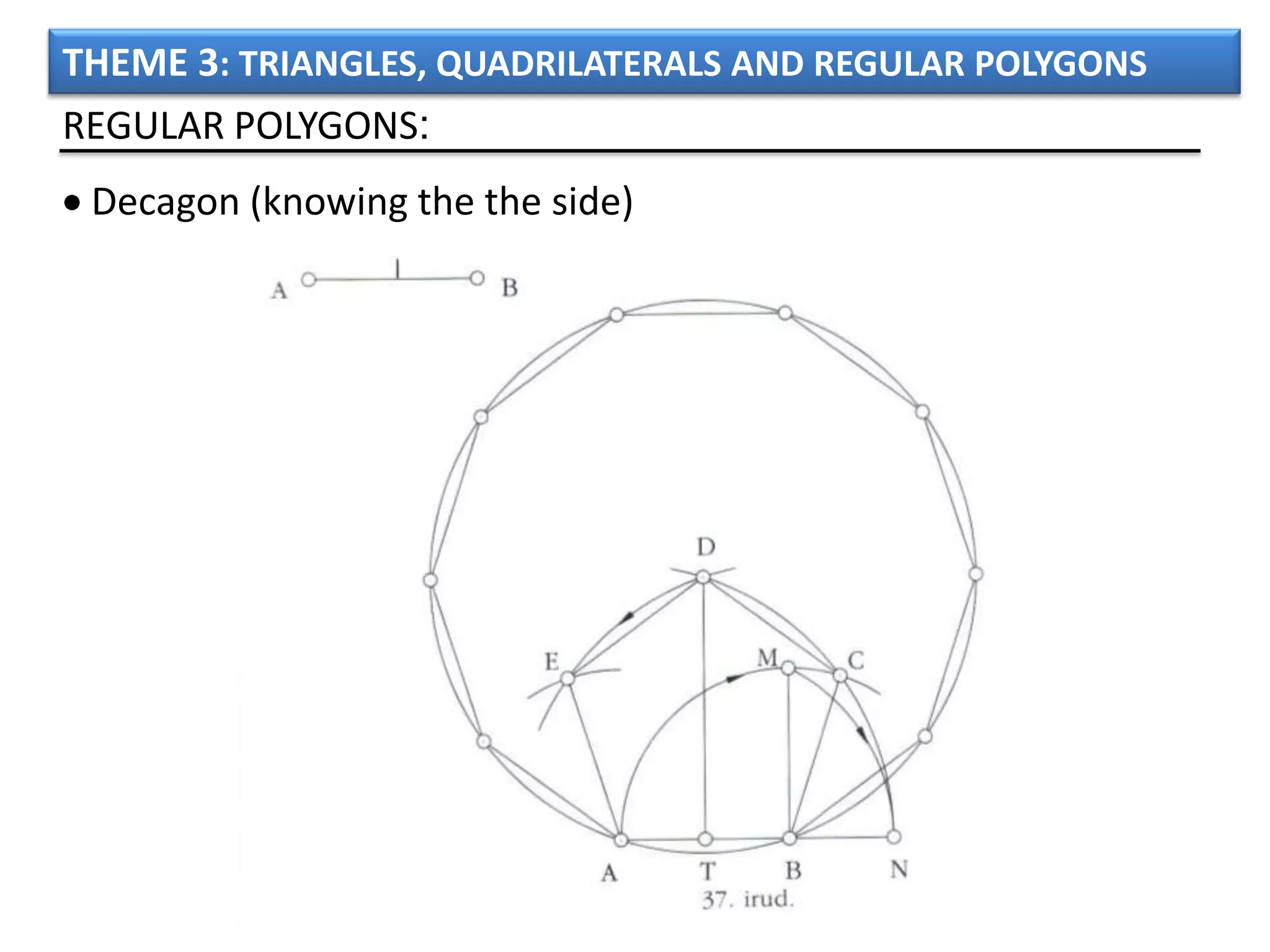
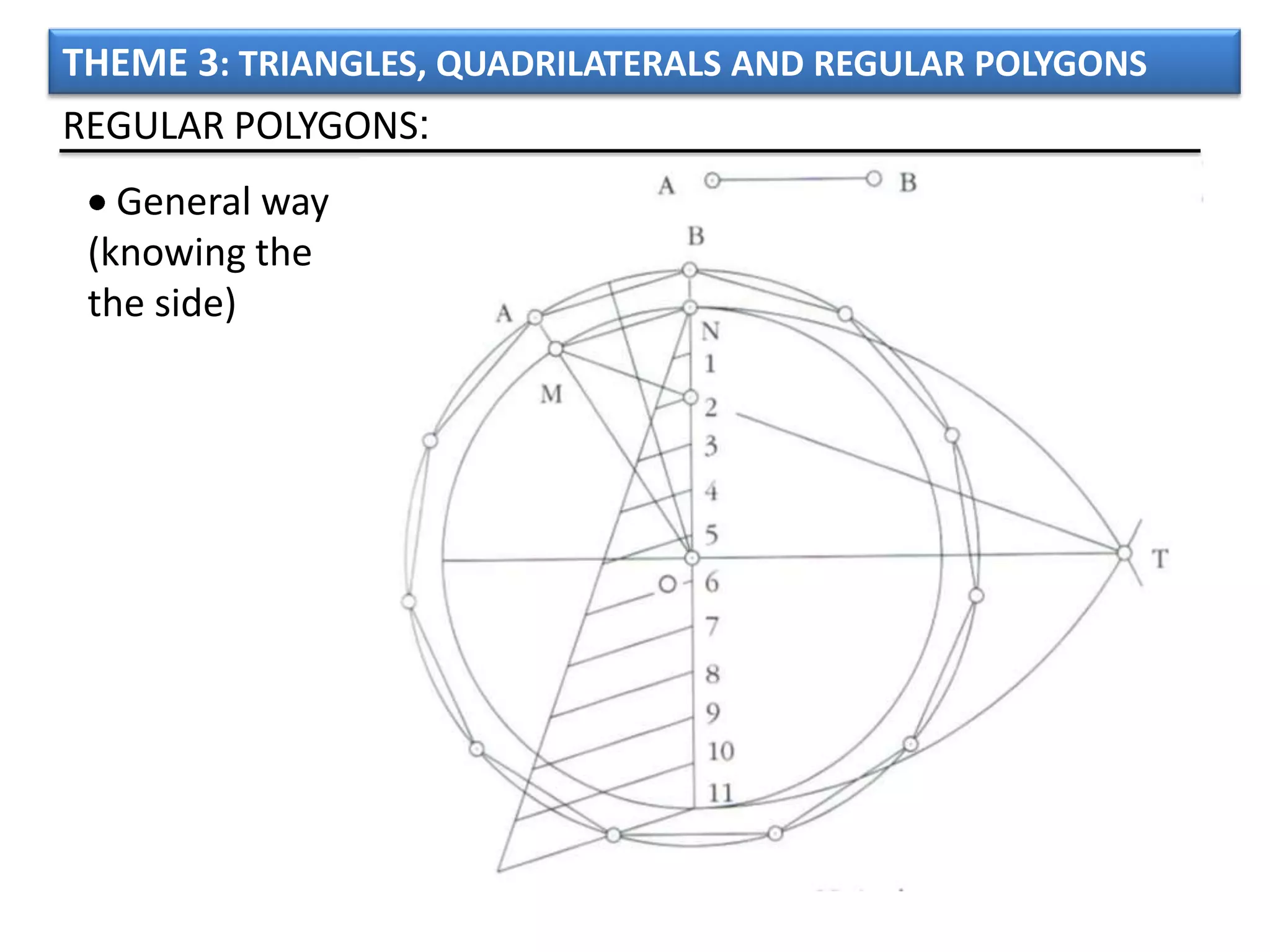
The document discusses basic geometric elements like points, lines, planes, and angles. It defines different types of lines and angles, and how to construct them. It also covers triangles, quadrilaterals, and regular polygons. For triangles, it defines different types and their important points and lines. For quadrilaterals, it categorizes different types like parallelograms, rectangles, and trapezoids. Finally, it discusses regular polygons and how to define them based on equal sides and angles.

1. TECHNICAL
DRAWING I

2. THEME 2: BASIC PATHS IN THE PLANE
Basic geometrics elements:
POINT:
A No dimension.
C
B It’s a position.
Always in CAPITAL letters.

3. THEME 2: BASIC PATHS IN THE PLANE
Basic geometrics elements:
LINE: It’s an addition of several
points following the same
r
direction.
Always in small letters; r, s, t…
r r
s r
A s
s
Two lines cut each Two lines can be When the two lines
other when they share parallel when the share no point, they
a point. sharing point is in the cross each other.
infinite.

4. THEME 2: BASIC PATHS IN THE PLANE
Basic geometrics elements:
HALF LINE: One point is known and the
A
∞→ other is in the infinite.
r
A point in the line defines tow
←∞ A ∞→ half-lines, one to the left and
r the other to the right.
SEGMENT:
A B Is a kind of line defined
r between two known points.

5. THEME 2: BASIC PATHS IN THE PLANE
Basic geometrics elements:
CURVED LINE:
A curved line is a group of
points constantly changing
direction.
Always in small letters.

6. THEME 2: BASIC PATHS IN THE PLANE
Basic geometrics elements:
PLANE:
Is the set of points that arise when you move a straight
line in one direction.
We need the following information to define a plane:
Non aligned 3 points. Two lines cutting each other.
Two parallel lines. A line and a point out of the line.

7. THEME 2: BASIC PATHS IN THE PLANE
Lines within a plane:
Bisecting line:

8. THEME 2: BASIC PATHS IN THE PLANE
Lines within a plane:
To draw a perpendicular from “M” point outside the line:

9. THEME 2: BASIC PATHS IN THE PLANE
Lines within a plane:
To draw a perpendicular from “P” point inside the line:

10. THEME 2: BASIC PATHS IN THE PLANE
Lines within a plane:
To construct a perpendicular at the end of a given line:

11. THEME 2: BASIC PATHS IN THE PLANE
Lines within a plane:
● To draw parallel lines with the set squares:

12. THEME 2: BASIC PATHS IN THE PLANE
Lines within a plane:
● To draw perpendicular lines with the set squares:

13. THEME 2: BASIC PATHS IN THE PLANE
Basic geometrics elements:
ANGLES:
Is a measure of a turn. We use a protractor to measure an angle.
Sometimes we use letters from Greek alphabet to name angles; α, β, γ,
δ…
And sometimes we name (B) the vertex of the angle and (choosing A and C
points) on the two sides; we write ABC. So the angle reads ABC.
Different kind of angles:
Null angle: α = 0°
Acute angle: α < 90°
Right angle: α = 90°
Obtuse angle: α > 90°
Plain angle: α = 180°
Complete angle: α = 360°

14. THEME 2: BASIC PATHS IN THE PLANE
Basic geometrics elements:
ANGLES:
Two lines cutting each other at point O creates the following angles;
β
α γ
δ
 Adjacent angles: α and β. Same vertex and side in common.
 Angles opposite at vertex; α and γ; β and δ.
So, α and γ / β and δ are of the same value.

15. THEME 2: BASIC PATHS IN THE PLANE
Operations with angles :
To construct an angle similar to a given angle;

16. THEME 2: BASIC PATHS IN THE PLANE
Operations with angles :
Summing up angles;

17. THEME 2: BASIC PATHS IN THE PLANE
Operations with angles :
Difference between angles;

18. THEME 2: BASIC PATHS IN THE PLANE
Operations with angles :
To bisect an angle (bisector);

19. THEME 2: BASIC PATHS IN THE PLANE
Operations with angles :
To bisect an angle (bisector);

20. THEME 2: BASIC PATHS IN THE PLANE
Operations with angles :
Drawing angles;
60 angle: 90 angle:
45 angle: 30 angle:
15 angle: 75 angle:

21. THEME 2: BASIC PATHS IN THE PLANE
Operations with angles :
Drawing angles;
105 angle: 120 angle:
135 angle: 150 angle:

22. THEME 2: BASIC PATHS IN THE PLANE
Geometric places:
The set of points having the same geometric characteristics.
1. Circumference:
2. Bisecting line:

23. THEME 2: BASIC PATHS IN THE PLANE
Geometric places:
3. Bisector line:
4. The loci arc of a segment (depending on the angle):

24. THEME 2: BASIC PATHS IN THE PLANE
Circumference:
A circle is a plain figure bounded by a curved line called the
circumference, witch is always equidistant from the centre.
Lines of a circumference:
Radius; Any of the straight lines from the centre to
the circumferences. The radius is half the diameter of
the circumference.
Diameter: The longest possible chord of a
circumference. A line passing through the centre with
both ends touching the circumference.

25. THEME 2: BASIC PATHS IN THE PLANE
Circumference:
Chord: A straight line, witch each end touching the
circumference.
Arrow; It’s a part of the radius between the chord
and the circumference. The radius is perpendicular
to the chord.
Secant: A line that cuts the circumference at two
points.
Tangent: A line touching the circumference at one
point. Forms a right angle with a radius of the circle.
T is the point contact.

26. THEME 2: BASIC PATHS IN THE PLANE
Circumference:

27. THEME 2: BASIC PATHS IN THE PLANE
Circumference:
To construct a circumference when you have 3 points.

28. THEME 3: TRIANGLES, SQUARES AND REGULAR POLYGONS
TRIANGLES:
Is a polygon formed by three segments.
The addition of every inner angles of a triangle is always 180º.
α + β + γ = 180º
The value of the outside angle of a triangle is the addition of
the two non-adjacent inside angles.

29. THEME 3: TRIANGLES, SQUARES AND REGULAR POLYGONS
TRIANGLES:
In every triangle, any side is always smaller than the addition of
the other two;
a<b+c
And any side is larger than the subtraction of the other two;
b>a-c
In every triangle the larger angle is in front of the larger side;
c > a; γ > α

30. THEME 3: TRIANGLES, SQUARES AND REGULAR POLYGONS
CLASSIFICATION OF TRIANGLES:
Depending on sides;
Equilateral: Isosceles: Scalene:

31. THEME 3: TRIANGLES, SQUARES AND REGULAR POLYGONS
CLASSIFICATION OF TRIANGLES:
Depending on angles;
Acute:
Right:
Obtuse:

32. THEME 3: TRIANGLES, SQUARES AND REGULAR POLYGONS
REMARKABLE LINES AND POINTS OF A TRIANGLE:
Bisector / Incentre / Inscribed circle to a triangle.

33. THEME 3: TRIANGLES, SQUARES AND REGULAR POLYGONS
REMARKABLE LINES AND POINTS OF A TRIANGLE:
Bisecting line / Circumcentre / Circumscribed circle to a triangle.

34. THEME 3: TRIANGLES, SQUARES AND REGULAR POLYGONS
REMARKABLE LINES AND POINTS OF A TRIANGLE:
Altitudes / Orthocentre.

35. THEME 3: TRIANGLES, SQUARES AND REGULAR POLYGONS
REMARKABLE LINES AND POINTS OF A TRIANGLE:
Baricentre or Centre of Gravity.

36. THEME 3: TRIANGLES, SQUARES AND REGULAR POLYGONS
CONSTRUCTING TRIANGLES:
a) Knowing the 3
sides a, b and c.
b) Knowing 2 of the
sides and the angle
between them.
c) Knowing one
side, a, and the
angles B and C.

37. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
QUADRILATERAL:
It is an polygon formed by 4 sides.
QUADRILATERALS
Trapezium (two
PARALELOGRAM
sides are parallels, Trapezoid (no
(Two by two, sides
the other two parallel sides)
are parallel)
aren’t)

38. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
QUADRILATERAL:
Square
Rectangle.
PARALELOGRAM
(Two by two,
sides are parallel)
Rhombus.
Rhomboid

39. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
QUADRILATERAL:
Trapezium
(two sides are parallels, the other
two aren’t)
Isosceles
Right
Scalene

40. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
QUADRILATERAL:

41. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
What is a Polygon?
A closed plane figure made up of several line
segments that are joined together.
The sides do not cross each other.
Exactly two sides meet at every vertex.

42. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
One polygon is regular if all the sides and all the angles are equal.
l = Side.
a = Apoteme
r = Radius
α = 180º - (360º / n)
λ = 360º / n

43. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Regular Hexagon.

44. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Regular triangle; equilateral triangle.

45. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Dodecagon.

46. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Square.

47. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Octagon.

48. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Pentagon

49. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Decagon

50. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Heptagon

51. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
General way.

52. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Pentagon (knowing the the side)

53. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Hexagon (knowing the the side)

54. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Heptagon (knowing the the side)

55. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Octagon (knowing the the side)

56. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Nonagon, Enneagon (knowing the the side)

57. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
Decagon (knowing the the side)

58. THEME 3: TRIANGLES, QUADRILATERALS AND REGULAR POLYGONS
REGULAR POLYGONS:
General way
(knowing the
the side)