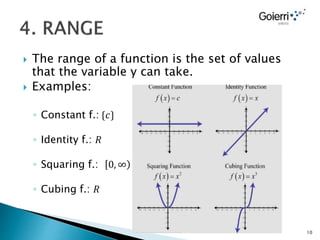
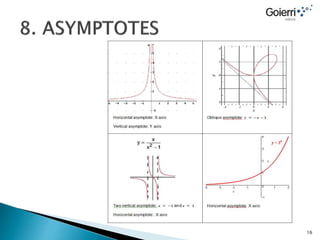
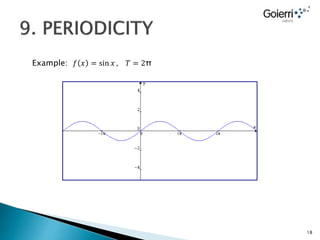
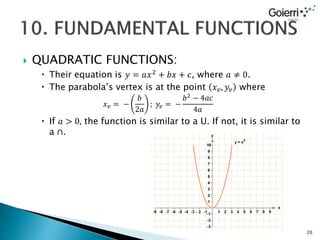
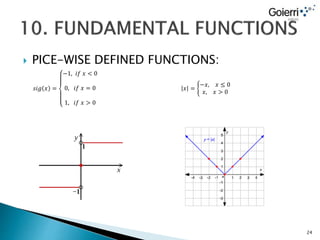
The document defines and explains key concepts related to functions including: - Functions map elements from the domain to a range. - The domain is the set of independent variables a function is defined for, which can be continuous or discrete. - The range is the set of output values the function can take. - Functions can have properties like being even, odd, continuous, increasing, decreasing, or periodic.

2.  It is a correspondence between two sets, A
and B.
 For each element in A, it assigns one, and
only one, element in B.
f : A → B
x → y = f (x)
2

3.  Being D any non-null subset of R, a real function is
any application from D to R.
 Tables and graphs are used to represent them.
f: D ⊆ R → R
x → y = f (x)
𝒚 = 𝒙 𝟐
x y
-2 4
-1 1
0 0
1 1
2 4
3

4.  It is a set of independent variables for which a
function is defined.
 There are two kinds of domains:
◦ Continuous: the function f is defined for an interval.
◦ Discrete: the function f is only defined for some
isolated values.
4

5.  Their domain is all R.
5

6.  𝑓 𝑥 =
𝑃 𝑥
𝑄 𝑥
 𝐷𝑜𝑚 𝑓 = 𝑅 − 𝑥 ∈ 𝑅/𝑄(𝑋) = 0
6

7.  𝑓 𝑥 = 𝑛
𝑔(𝑥)
 Their domain depends on n:
◦ If n is odd, 𝐷𝑜𝑚 𝑓 = 𝐷𝑜𝑚 𝑔
◦ If n is even, 𝐷𝑜𝑚 𝑓 = 𝑥 ∈ 𝐷𝑜𝑚 𝑔(𝑥)/𝑔(𝑥) ≥ 0
7

8.  𝑓 𝑥 = 𝑎 𝑔 𝑥 , 𝑤ℎ𝑒𝑟𝑒 𝑎 > 0 𝑎𝑛𝑑 𝑎 ≠ 1.
 𝐷𝑜𝑚 𝑓 = 𝐷𝑜𝑚(𝑔)
8

9.  f ( x ) = loga [g ( x )], where a > 0, a ≠1.
 Dom(f )={x ∈Dom(g ) / g( x )> 0}
9

10.  The range of a function is the set of values
that the variable y can take.
 Examples:
◦ Constant f.: {𝑐}
◦ Identity f.: 𝑅
◦ Squaring f.: 0, ∞
◦ Cubing f.: 𝑅
10

11.  If 𝑓 𝑥 = 𝑓 −𝑥 for all 𝑥𝜖𝐷𝑜𝑚(𝑓), then the
function is EVEN, symmetric to the Y axis.
 If 𝑓 −𝑥 = −𝑓 𝑥 for all 𝑥𝜖𝐷𝑜𝑚(𝑓), then the
function is ODD, symmetric to the origin.
 It can also be symmetric to the X axis.
11

12.  Continuous function: a function without gaps.
◦ Polynomial functions
◦ Exponential functions
◦ …
 Non continuous function: a function with
gaps.
◦ Rational functions
◦ …
12

13.  Essentially increasing:
𝑓 𝑥1 − 𝑓(𝑥2)
𝑥1 − 𝑥2
> 0
 Increasing:
𝑓 𝑥1 − 𝑓(𝑥2)
𝑥1 − 𝑥2
≥ 0
13

14.  Essentially decreasing:
𝑓 𝑥1 − 𝑓(𝑥2)
𝑥1 − 𝑥2
< 0
 Decreasing:
𝑓 𝑥1 − 𝑓(𝑥2)
𝑥1 − 𝑥2
≤ 0
14

15. Relative maximum: (0, 0)
Absolute minimums: (-1,-4) and (1,-4)
Absolute minimum: (0,-4)
Relative minimum: (1, 2)
Relative maximum: (-1,-2)
It has no maximums or minimums.
15

16. 16

17.  The function F is said to be a periodic
function with period T, where T≠0, if:
◦ 𝑥 ∈ 𝐷𝑜𝑚 𝑓 𝑥 + 𝑇 ∈ 𝐷𝑜𝑚 (𝑓)
◦ 𝑓 𝑥 = 𝑓 𝑥 + 𝑇 , ∀𝑥 ∈ 𝐷𝑜𝑚 𝑓
◦ T is the smallest real number that fulfils those two
conditions.
17

18. Example: 𝑓 𝑥 = sin 𝑥 , 𝑇 = 2π
18

19.  LINEAR FUNCTIONS:
• Their equation is 𝑦 = 𝑚𝑥 + 𝑛.
• m is the slope of the line and it cuts the Y axis
at the point (0,n)
• If 𝑚 > 0, the function is increasing, and if 𝑚 < 0
it is decreasing.
19

20.  QUADRATIC FUNCTIONS:
 Their equation is 𝑦 = 𝑎𝑥2
+ 𝑏𝑥 + 𝑐, where 𝑎 ≠ 0.
 The parabola’s vertex is at the point 𝑥 𝑣, 𝑦𝑣 where
𝑥 𝑣 = −
𝑏
2𝑎
; 𝑦𝑣 = −
𝑏2 − 4𝑎𝑐
4𝑎
 If 𝑎 > 0, the function is similar to a U. If not, it is similar to
a ∩.
20

21.  K/X TYPE FUNCTIONS:
 𝑥 = 0 is not in the domain.
 It doesn’t cut the X axis, because 𝑘/𝑥 ≠ 0 for
every x.
 It is an odd symmetry function.
21

22.  EXPONENTIAL FUNCTIONS:
 Their equation is 𝑓 𝑥 = 𝑎 𝑥, where a>0 and 𝑎 ≠ −1.
 They do not cut the X axis, because the equation 𝑎 𝑥
= 0
has no real solutions.
 They cut the Y axes at the point (0,1).
 LOGARITHMIC FUNCTIONS:
 Their equation is 𝑓 𝑥 = log 𝑎 𝑥, where a>0 and a≠1.
 They cut the X axis at the point (1, 0).
 They go through the point (a, 1).
22

23.  TROGONOMETRIC FUNCTIONS:
23

24.  PICE-WISE DEFINED FUNCTIONS:
𝑠𝑖𝑔 𝑥 =
−1, 𝑖𝑓 𝑥 < 0
0, 𝑖𝑓 𝑥 = 0
1, 𝑖𝑓 𝑥 > 0
𝑥 =
−𝑥, 𝑥 ≤ 0
𝑥, 𝑥 > 0
24

25.  𝑓 + 𝑔 𝑥 = 𝑓 𝑥 + 𝑔 𝑥 ∀𝑥 ∈ [𝐷𝑜𝑚 𝑓 ∩ 𝐷𝑜𝑚 𝑔 ]
 −𝑓 𝑥 = −𝑓(𝑥)
 𝑓 − 𝑔 𝑥 = 𝑓 𝑥 + −𝑔 𝑥 , ∀𝑥 ∈ [𝐷𝑜𝑚 𝑓 ∩ 𝐷𝑜𝑚 𝑔 ]
 𝑓 · 𝑔 𝑥 = 𝑓 𝑥 · 𝑔 𝑥
 (1/𝑓) 𝑥 =1/𝑓(𝑥)
 (f/g) 𝑥 = 𝑓 𝑥 ·1/𝑔 𝑥 = 𝑓(𝑥)/𝑔(𝑥)
25

26.  Being 𝑓 and 𝑔 two functions of real variables
with domains 𝐷1 and 𝐷2 domains
respectively, and with 𝑓(𝐷1) ≤ 𝐷2; the
compose function is:
𝑔°𝑓 𝑥 = 𝑔[𝑓 𝑥 ]
26

27. 27