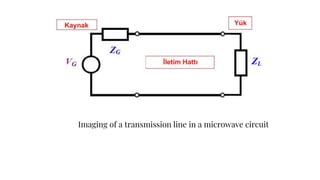
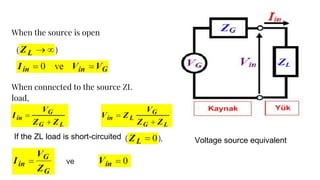
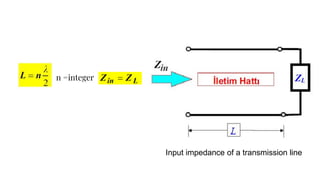
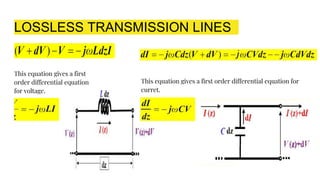
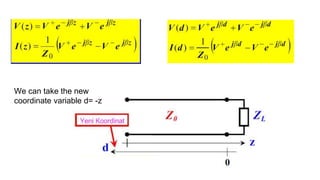
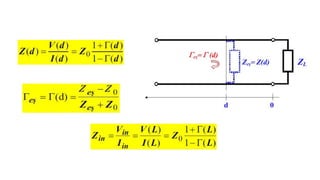
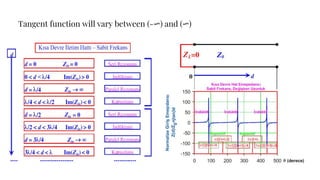
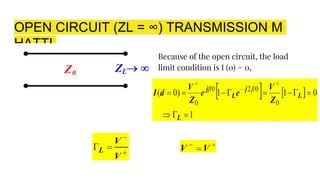
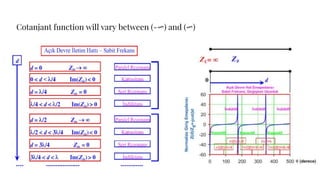
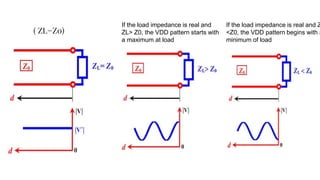
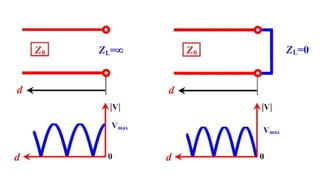
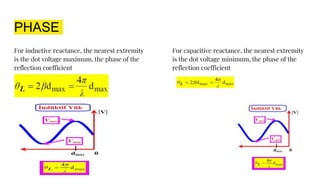
The document discusses parameters plotted on the Smith Chart such as reflection coefficient magnitude and phase, transmission line length, VSWR, and input impedance. It examines voltage and current on transmission lines for different load conditions like open circuit, short circuit, and matched loads. Equations are presented for voltage and current on lossless transmission lines, and for calculating standing wave ratios and reflection coefficients. The behavior of voltage standing wave patterns and phase are described depending on the load impedance characteristics.

1. The Complex
Reflection Coefficient

2. Parameters Plotted on SMITH CHART
➢ Paraneters plotted on the Smith Chart include the following:
❏ Reflection coefficient magnitude ,Γ
❏ Reflection coefficient phase angle ,Q
❏ Lenght of transmission line between any two points in wavelength
❏ VSWR
❏ Input Impedance Zin
❏ The location of Vmax and Vmin (dmax - dmin)

3. Imaging of a transmission line in a microwave circuit

4. TRANSMISSION STATISTICS AND
TRANSMISSION STATISTICS EQUATIONS
The impedance
properties of
conductors can
not be neglected
The voltage values on a transmission line in microwave frequencies

5. When the source is open
When connected to the source ZL
load,
Voltage source equivalentIf the ZL load is short-circuited

6. n =integer
Input impedance of a transmission line

7. LOSSLESS TRANSMISSION LINES
This equation gives a first
order differential equation
for voltage.
This equation gives a first order differential equation for
curret.

8. General solution for voltage
equation is ;
Here, the propagation
constant of the waveguide,
By differentiating the result obtained
for the voltage

9. We can take the new
coordinate variable d= -z

10. the voltage load reflection coefficient;
Thus, line equations

12. SHORT CIRCUIT (ZL=0) TRANSMISSION LINE
Due to the short circuit,
the load limit V (0) = 0
and as a result
Thus, the phasor of the line voltage

13. Thus, line impedance;
ZL = 0

14. Tangent function will vary between (-∞) and (∞)

15. OPEN CIRCUIT (ZL = ∞) TRANSMISSION M
HATTI
Because of the open circuit, the load
limit condition is I (0) = 0,

16. Thus, the line current phase
image
Thus, line voltage;
since the impedance function is
also periodic, the impedance will
repeat the behavior identical at
every lambda / 2 distance.

17. Cotanjant function will vary between (-∞) and (∞)

18. Standing Wave
SW represents the maximum value of
the voltage or current that occurs at
each point of the transmission line.
Incoming and reflected waves.Due to the structure and destructive
interventions, it is repeated in space with the λ / 2 period.
Generalized reflection coefficient,
The amplitude of an exponential
term with an image argument is
always one (Maximum)
Minimum point

19. ( ZL=Z0)
If the load impedance is real and
ZL> Z0, the VDD pattern starts with
a maximum at load
If the load impedance is real and Z
<Z0, the VDD pattern begins with a
minimum of load

21. VSWR(VOLATGE STANDING WAVE)
That is, an indicator of maximum energy transfer and is denoted by the letter S.
If the load impedance is perfectly matched to the transmission line;
If the load is terminated by short circuit, open circuit or pure reactance

22. PHASE
For inductive reactance, the nearest extremity
is the dot voltage maximum, the phase of the
reflection coefficient
For capacitive reactance, the nearest extremity
is the dot voltage minimum, the phase of the
reflection coefficient