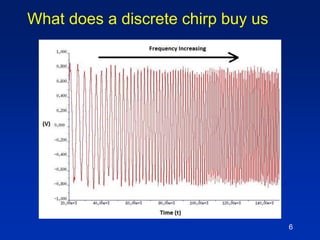
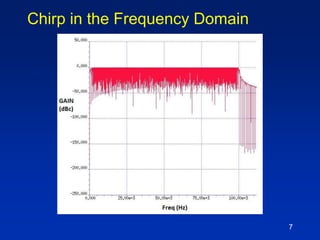
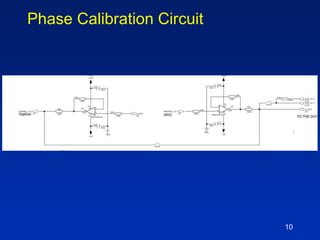
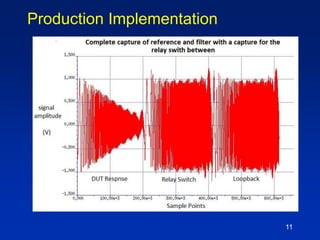
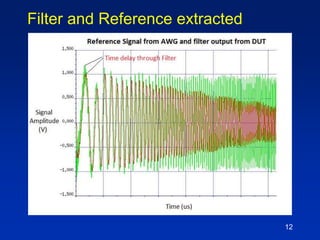
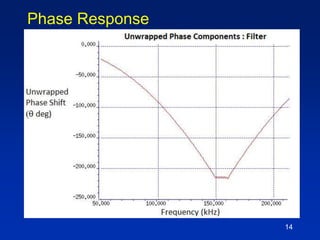
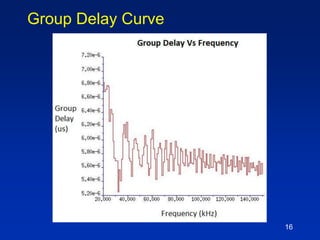
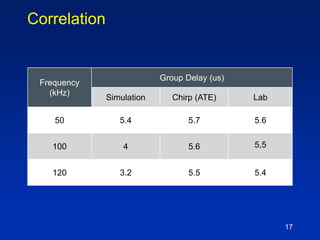
The document describes a technique for characterizing group delay filters using a discrete chirped excitation signal, aiming to improve testing efficiency and data reusability. It explains the standard measurement methods, introduces discrete chirp generation, and emphasizes phase calibration to enhance accuracy. The conclusion highlights that this method yields reliable and comprehensive characterization data, saving significant test time in semiconductor design.

1. Test time efficient group
delay filter characterization
technique using a discrete
chirped excitation signal
2016 International Test Conference
November 16th
Peter Sarson

2. 2
Outline
 What problem are we trying to resolve
 How to measure phase based metrics
 What does a discrete chirp buy us
 How to generate a chirp
 Implementation
 Measurements
 Correlation and stability
 Conclusion

3. 3
What problem are we addressing
 Produce a Group Delay production style test
• That gives full characterization data
• That is faster than the standard approach
• That can be reused easily like an IP Block
 Save coding time for future projects
 Remove last minute requests for
characterization tests

4. 4
What is group delay
 group delay is a measure of the slope of the
phase response at any given frequency
• Tg = -d /d
Therefore – need to sweep filter frequency
range to get characterization data

5. 5
Standard Method
 Start and Stop of AWG for each and
individual Frequency of interest
 Full Digitizer capture for each frequency
 Long Test Time for a few or many
frequencies

6. What does a discrete chirp buy us
6

7. Chirp in the Frequency Domain
7

8. 8
How to generate a discrete chirp
 By using the coherence formula we can build
a discrete chirp using Ff
• Fs/Ft = N/M - Coherence Condition
• Ff = Fs/N - Fourier Freq - Resolution
• r = 2/N - Phase Resolution
If we build a wavelet by making sinewaves a
multiples of Ff we will produce a discrete
chirp

9. 9
Phase Calibration
 As the starting phase of the AWG is unknown
• We need to somehow remove the starting
phase
 By making a loopback circuit
• We can capture the source waveform
• and device response
• In one capture
 Hence subtracting the two removes the
starting phase of the AWG

10. 10
Phase Calibration Circuit

11. 11
Production Implementation

12. 12
Filter and Reference extracted

13. 13
Points to note
 To get from an FFT to real phase
• We need to phase unwrap the signal
• If the phase resolution is to small this will
not be possible
 The phase response is described as
•  (t) =0 + 2( f0t + kt2/2)

14. 14
Phase Response

15. 15
Time delay through filter

16. 16
Group Delay Curve

17. 17
Correlation
Frequency
(kHz)
Group Delay (us)
Simulation Chirp (ATE) Lab
50 5.4 5.7 5.6
100 4 5.6 5,5
120 3.2 5.5 5.4

18. Stability
18

19. Reproducibility
19

20. Test Time Saving
 AWG setup time is 2ms
• UTP of waveform is negligible in time
• So 5 frequencies for Group Delay is 10ms
 Using a chirp
• You only setup once
• Therefore more frequencies that are of
interest the more the chirp is cost effective
20

21. Conclusion
 Using a chirp for group delay measurements
gives reliable, accurate and reproducible
results that is not only test time efficient but
also gives full characterization data that is
priceless to a semiconductor integrated circuit
designer.
21

22. Confidential © ams AG
Thank you
 Please visit our website www.ams.com