Downloaded 831 times
Uploaded byWALTER HUGO MELGAREJO VELASQUEZ
Aashto design
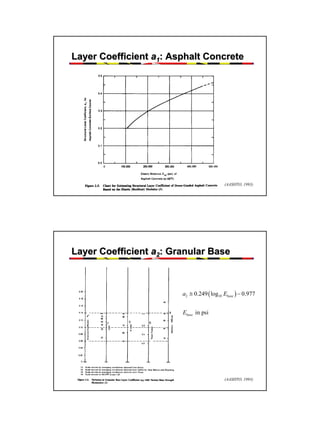
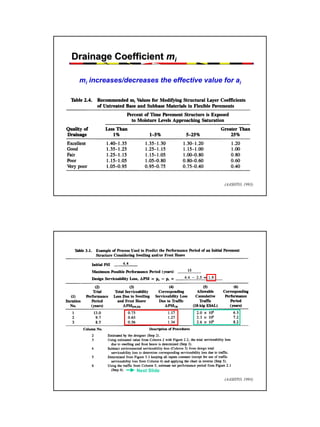
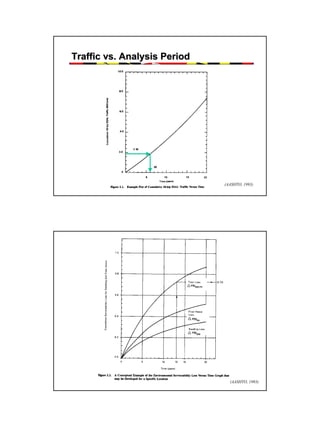
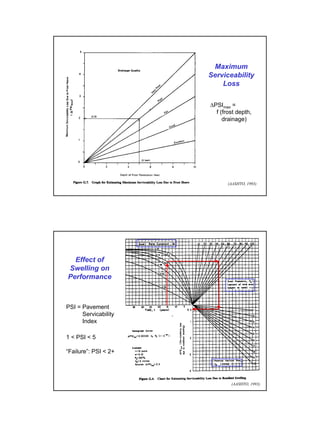
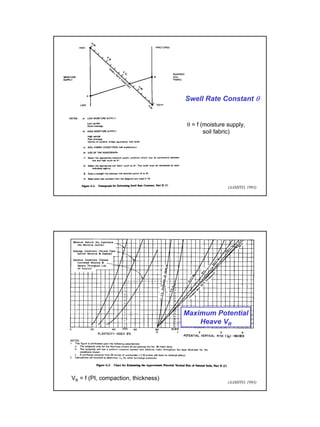
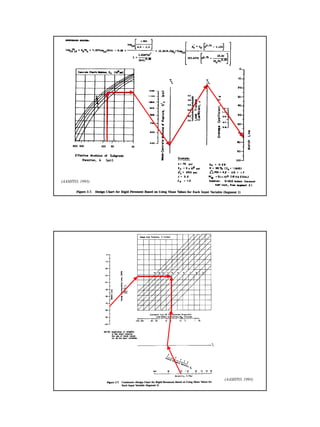
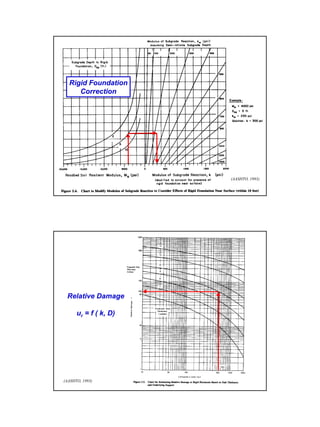
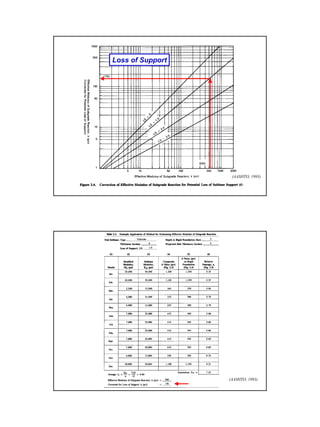
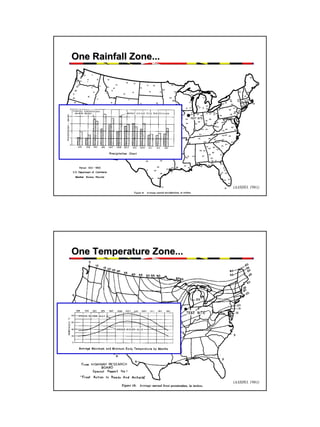
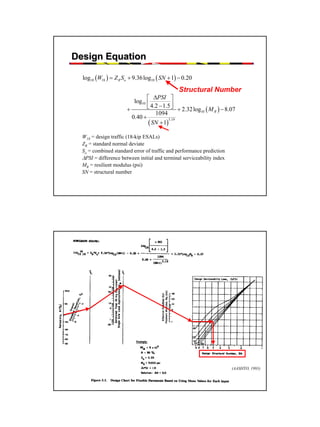
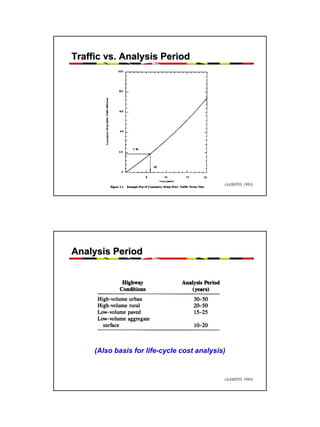
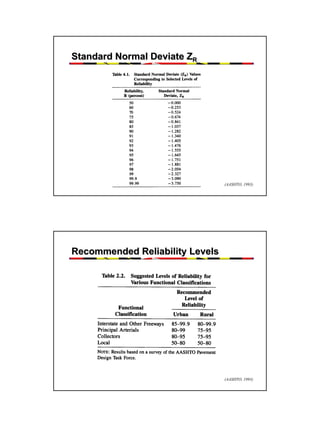
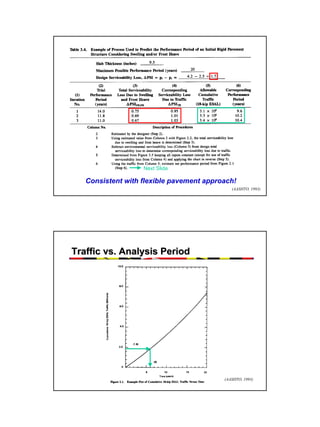
This document provides an overview of pavement design methods and the 1993 AASHTO Guide for pavement design of both flexible and rigid pavements. It summarizes: - The objectives and inputs considered in pavement design - The empirical and mechanistic-empirical approaches used in the AASHTO Guide - The key equations, parameters, and design process for both flexible and rigid pavement structures It describes how the AASHTO Guide is based on predicting the decrease in serviceability over time under traffic loading using reliability concepts. The design process involves calculating the structural number for flexible pavements or slab thickness for rigid pavements based on traffic, materials properties, and reliability factors.
More Related Content
Aashto design
- 1. Design Methods • HighwayPavements AASHTO The Asphalt Institute Portland Cement Association • Airfield Pavements FAA The Asphalt Institute Portland Cement Association U.S. Army Corps of Engineers Objectives of Pavement Design To provide a surface that is: • Strong Surface strength Moisture control • Smooth • Safe Friction Drainage • Economical Initial construction cost Recurring maintenance cost 1
- 2. Pavements are Designed toFail !! Pavement Design Methodologies • Experience • Empirical Statistical models from road tests • Mechanistic-Empirical Calculation of pavement stresses/strains/deformations Empirical pavement performance models • Mechanistic Calculation of pavement stresses/strains/deformations Mechanics-based pavement performance models 2
- 3. Empirical vs. MechanisticDesign P d L Wood Floor Joist Empirical “Rule of 2”: d in inches= (L in feet / 2) + 2 Mechanistic: σbending = PL ≤ σ allowable 4S 1993 Version 3
- 4. AASHTO Pavement DesignGuide • Empirical design methodology • Several versions: 1961 (Interim Guide) 1972 1986 Refined material characterization Version included in Huang (1993) 1993 More on rehabilitation More consistency between flexible, rigid designs Current version 2002 Under development Will be based on mechanistic-empirical approach AASHO Road Test (late 1950’s) (AASHO, 1961) 4
- 5. One Rainfall Zone... (AASHO,1961) One Temperature Zone... (AASHO, 1961) 5
- 6. One Subgrade... A-6 /A-7-6 (Clay) Poor Drainage (AASHO, 1961) Limited Set of Materials... • One asphalt concrete 3/4” surface course 1” binder course • One Portland cement concrete (3500 psi @ 14 days) • Four base materials Well-graded crushed limestone (main experiment) Well-graded uncrushed gravel (special studies) Bituminous-treated base (special studies) Cement-treated base (special studies) • One uniform sand/gravel subbase 6
- 7.
- 8. Axle Loads (Thousands) LimitedTraffic Volumes... 1.1M Axles 1.1M Axles 2 Years 2 Years Time (Months) (AASHO, 1961) 1950’s Data Analysis... (AASHO, 1961) 8
- 9. Some Failures... (Some pavementstoo!) (AASHO, 1961) AASHTO Design Based on Serviceability Decrease (AASHTO, 1993) 9
- 10. What is Serviceability? •Based upon Present Serviceability Rating (PSR) • Subjective rating by individual/panel Initial/post-construction Various times after construction • 0 < PSR < 5 • PSR < ~2.5: Unacceptable (AASHO, 1961) Present Serviceability Index (PSI) • PSR correlated to physical pavement measures via Present Serviceability Index (PSI): 2 PSI = 5.03 − 1.91log(1 + SV ) − 1.38 RD − 0.01(C + P)1/ 2 SV = slope variance (measure of roughness) Empirical! RD = average rut depth (inches) C + P = area of cracking and patching per 1000 ft 2 PSI ≈ PSR 10
- 11. AASHTO Design Guide(1993) Part I: Pavement Design and Management Principles • Introduction and Background • Design Related to Project Level Pavement Management • Economic Evaluation of Alternative Design Strategies • Reliability AASHTO Design Guide (1993) Part II: Pavement Design Procedures for New Construction or Reconstruction • Design Requirements • Highway Pavement Structural Design • Low-Volume Road Design 11
- 12. AASHTO Design Guide(1993) Part III: Pavement Design Procedures for Rehabilitation of Existing Pavements • Rehabilitation Concepts • Guides for Field Data Collection • Rehabilitation Methods Other Than Overlay • Rehabilitation Methods With Overlays Design Scenarios Included in AASHTO Guide (AASHTO, 1993) 12
- 13. AASHTO Design Based onServiceability Decrease (AASHTO, 1993) Flexible Pavements 13
- 14. Design Equation log10 (W18) = Z R So + 9.36 log10 ( SN + 1) − 0.20 Structural Number ∆PSI log10 4.2 − 1.5 + 2.32 log M − 8.07 + 10 ( R) 1094 0.40 + 5.19 ( SN + 1) W18 = design traffic (18-kip ESALs) ZR = standard normal deviate So = combined standard error of traffic and performance prediction ∆PSI = difference between initial and terminal serviceability index MR = resilient modulus (psi) SN = structural number (AASHTO, 1993) 14
- 15. Traffic vs. AnalysisPeriod (AASHTO, 1993) Analysis Period (Also basis for life-cycle cost analysis) (AASHTO, 1993) 15
- 16. Design Traffic (18KESALs) (AASHTO, 1993) Design Traffic (18K ESALs) • DD = 0.5 typically • DL: (AASHTO, 1993) 16
- 17. Reliability (AASHTO, 1993) Recommended Valuesfor Standard Error So • Rigid Pavements: 0.30 - 0.40 • Flexible Pavements: 0.40 - 0.50 17
- 18. Standard Normal DeviateZR (AASHTO, 1993) Recommended Reliability Levels (AASHTO, 1993) 18
- 19. Serviceability ∆PSI = po− pt • PSI = Pavement Serviceability Index, 1 < PSI < 5 • po = Initial Serviceability Index Rigid pavements: 4.5 Flexible pavements: 4.2 • pt = Terminal Serviceability Index (AASHTO, 1993) Adjustment of Roadbed (Subgrade) MR for Seasonal Variations (AASHTO, 1993) 19
- 20. Structural Number n SN =a1 D1 + ∑ ai Di mi i =2 SN = structural number = f (structural capacity) ai = ith layer coefficient Di = ith layer thickness (inches) mi = ith layer drainage coefficient n = number of layers (3, typically) No Unique Solution! (AASHTO, 1993) 20
- 21. Layer Coefficient a1:Asphalt Concrete (AASHTO, 1993) Layer Coefficient a2: Granular Base a2 ≅ 0.249 ( log10 Ebase ) − 0.977 Ebase in psi (AASHTO, 1993) 21
- 22. Layer Coefficient a2:Cement Treated Base (AASHTO, 1993) Layer Coefficient a2: Bituminous Treated Base (AASHTO, 1993) 22
- 23. Layer Coefficient a3:Granular Subbase a3 = 0.227(log10 Esubbase ) − 0.839 Esubbase in psi (AASHTO, 1993) Quality of Drainage (AASHTO, 1993) 23
- 24. Drainage Coefficient mi miincreases/decreases the effective value for ai (AASHTO, 1993) Next Slide (AASHTO, 1993) 24
- 25. Traffic vs. AnalysisPeriod (AASHTO, 1993) (AASHTO, 1993) 25
- 26. Effect of Frost onPerformance PSI = Pavement Servicability Index 1 < PSI < 5 “Failure”: PSI < 2+ (AASHTO, 1993) Frost Heave Rate φ φ = f (-0.02mm) (AASHTO, 1993) 26
- 27. Maximum Serviceability Loss ∆PSImax = f (frostdepth, drainage) (AASHTO, 1993) Effect of Swelling on Performance PSI = Pavement Servicability Index 1 < PSI < 5 “Failure”: PSI < 2+ (AASHTO, 1993) 27
- 28. Swell Rate Constantθ θ = f (moisture supply, soil fabric) (AASHTO, 1993) Maximum Potential Heave VR VR = f (PI, compaction, thickness) (AASHTO, 1993) 28
- 29. Rigid Pavements Design Equation log10(W18 ) = Z R So + 7.35log10 ( D + 1) − 0.06 PCC Thickness ∆PSI log10 ' 0.75 S c Cd ( D − 1.132 ) 4.5 − 1.5 + 4.22 − 0.32 p log + ( t) 10 1.64x107 0.75 18.42 1+ 8.46 215.63 J D − 0.25 ( D + 1) ( Ec / k ) W18 = design traffic (18-kip ESALs) ZR = standard normal deviate Sc’ = modulus of rupture (psi) for Portland cement concrete So = combined standard error of traffic and performance prediction J = load transfer coefficient D = thickness (inches) of pavement slab Ec = modulus of elasticity (psi) for Portland cement concrete ∆PSI = difference between initial and terminal serviceability indices pt = terminal serviceability value Cd = drainage coefficient k = modulus of subgrade reaction (pci) 29
- 30.
- 31. Design Inputs W18 =design traffic (18-kip ESALs) ZR = standard normal deviate So = combined standard error of traffic and performance prediction ∆PSI = difference between initial and terminal serviceability indices pt = terminal serviceability index (implicit in flexible design) All consistent with flexible pavements! Additional Design Inputs • S′c = modulus of rupture for concrete • J = joint load transfer coefficient • Cd = drainage coefficient (similar in concept to flexible pavement terms) • Ec = modulus of elasticity for concrete • k = modulus of subgrade reaction Additional inputs reflect differences in materials and structural behavior. 31
- 32. Modulus of Rupture Sc’ (AASHTO,1993) Joint Load Transfer Coefficient J Pavement Type (no tied shoulders) JCP/JRCP w/ load transfer devices JCP/JRCP w/out load transfer devices CRCP J 3.2 3.8-4.4 2.9 32
- 33. Joint Load TransferCoefficient J Additional benefits of tied shoulders: (AASHTO, 1993) Drainage Coefficient Cd • Two effects: Subbase and subgrade strength/stiffness Joint load transfer effectiveness (AASHTO, 1993) 33
- 34. PCC Modulus ofElasticity Ec • Measure directly per ASTM C469 • Correlation w/ compressive strength: Ec = 57,000 (fc’)0.5 Ec = elastic modulus (psi) fc’ = compressive strength (psi) per AASHTO T22, T140, or ASTM C39 Effective Subgrade Modulus k • Depends on: Roadbed (subgrade) resilient modulus, MR Subbase resilient modulus, ESB • Both vary by season 34
- 35. Determining Effective k(See Table 3.2) • Identify: Subbase types Subbase thicknesses Loss of support, LS (erosion potential of subbase) Depth to rigid foundation (feet) • Assign roadbed soil resilient modulus (MR) for each season • Assign subbase resilient modulus (ESB) for each season 15,000 psi (spring thaw) < ESB < 50,000 psi (winter freeze) ESB < 4(MR) (AASHTO, 1993) 35
- 36. Determining Effective k(cont’d) • Determine composite k for each season For DSB = 0: k = MR/19.4 For DSB > 0: Use Figure 3.3 • If depth to rigid foundation < 10 feet, correct k for effect of rigid foundation near the surface (Figure 3.4) • Estimate required thickness of slab (Figure 3.5) and determine relative damage ur for each season • Use average ur to determine effective k (Figure 3.5) • Correct k for potential loss of support LS (Figure 3.6) Composite Modulus of Subgrade Reaction k = f (MR , ESB , DSB ) (AASHTO, 1993) 36
- 37. Rigid Foundation Correction (AASHTO, 1993) RelativeDamage ur = f ( k, D) (AASHTO, 1993) 37
- 38. (AASHTO, 1993) Loss ofSupport, LS Subbase/subgrade erosion at joints causes Loss of Support, impairs load transfer. (AASHTO, 1993) 38
- 39. Loss of Support (AASHTO,1993) (AASHTO, 1993) 39
- 40. Next Slide Consistent withflexible pavement approach! (AASHTO, 1993) Traffic vs. Analysis Period (AASHTO, 1993) (AASHTO, 1993) 40
- 41. Joint Design • JointTypes Contraction Expansion Construction Longitudinal • Joint Geometry Spacing Layout (e.g., regular, skewed, randomized) Dimensions • Joint Sealant Dimensions Types of Joints • Contraction Transverse For relief of tensile stresses • Expansion Transverse For relief of compressive stresses Used primarily between pavement and structures (e.g., bridge) • Construction • Longitudinal For relief of curling and warping stresses 41
- 42. Typical Contraction JointDetails (Huang, 1993) Typical Expansion Joint Detail (Huang, 1993) 42
- 43. Typical Construction JointDetail (Huang, 1993) Typical Longitudinal Joint Detail Full Width Construction (Huang, 1993) 43
- 44. Typical Longitudinal JointDetail Lane-at-a-Time Construction (Huang, 1993) Joint Spacing • Local experience is best guide • Rules of thumb: JCP joint spacing (feet) < 2D (inches) W/L < 1.25 44
- 45. Joint Dimensions • Widthcontrolled by joint sealant extension • Depths: Contraction joints: D/4 Longitudinal joints: D/3 • Joints may be formed by: Sawing Inserts Forming Joint Sealant Dimension Governed by expected joint movement, sealant resilience (AASHTO, 1993) 45
- 46. Design Inputs Z αc (AASHTO, 1993) ReinforcementDesign (JRCP) • Purpose of reinforcement is not to prevent cracking, but to hold tightly closed any cracks that may form • Physical mechanisms: Thermal/moisture contraction Friction resistance from underlying material • Design based on friction stress analysis (Huang, 1993) 46
- 47. Dowel Bars: TransverseJoint Load Transfer • “…size and spacing should be determined by the local agency’s procedures and/or experience.” • Guidelines: Dowel bar diameter = D/8 (inches) Dowel spacing: 12 inches Dowel length: 18 inches Friction Stresses Induces tensile stresses in concrete Causes opening of transverse joints (Huang, 1993) 47
- 48. Applies to bothlongitudinal and transverse steel reinforcement (Generally, Ps=0 for L< ~15 feet) (AASHTO, 1993) Friction Factor (AASHTO, 1993) 48
- 49. Steel Working Stress Basedon preventing fracture and limiting permanent deformation. (AASHTO, 1993) Transverse Tie Bars (AASHTO, 1993) 49
- 50.