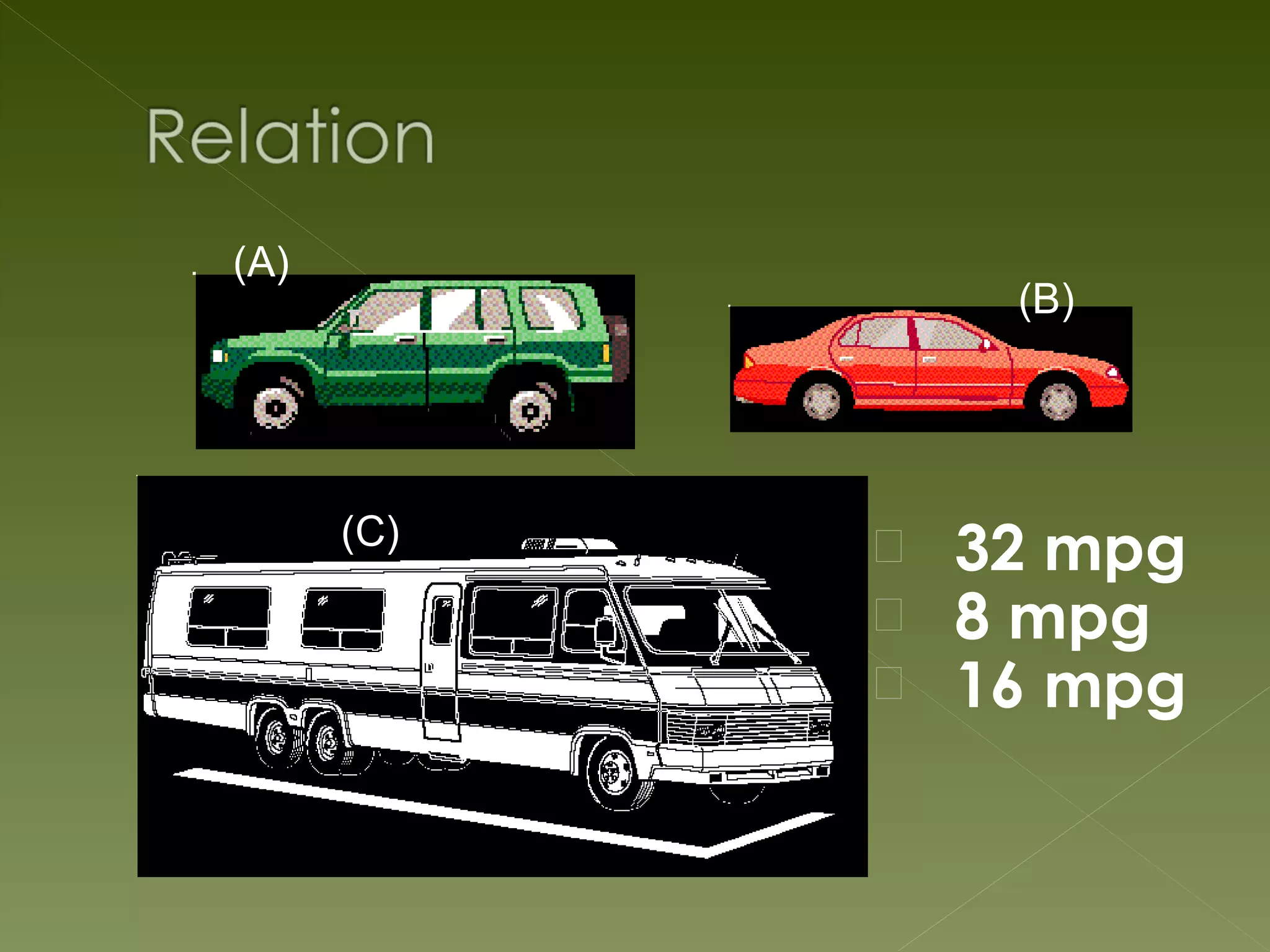
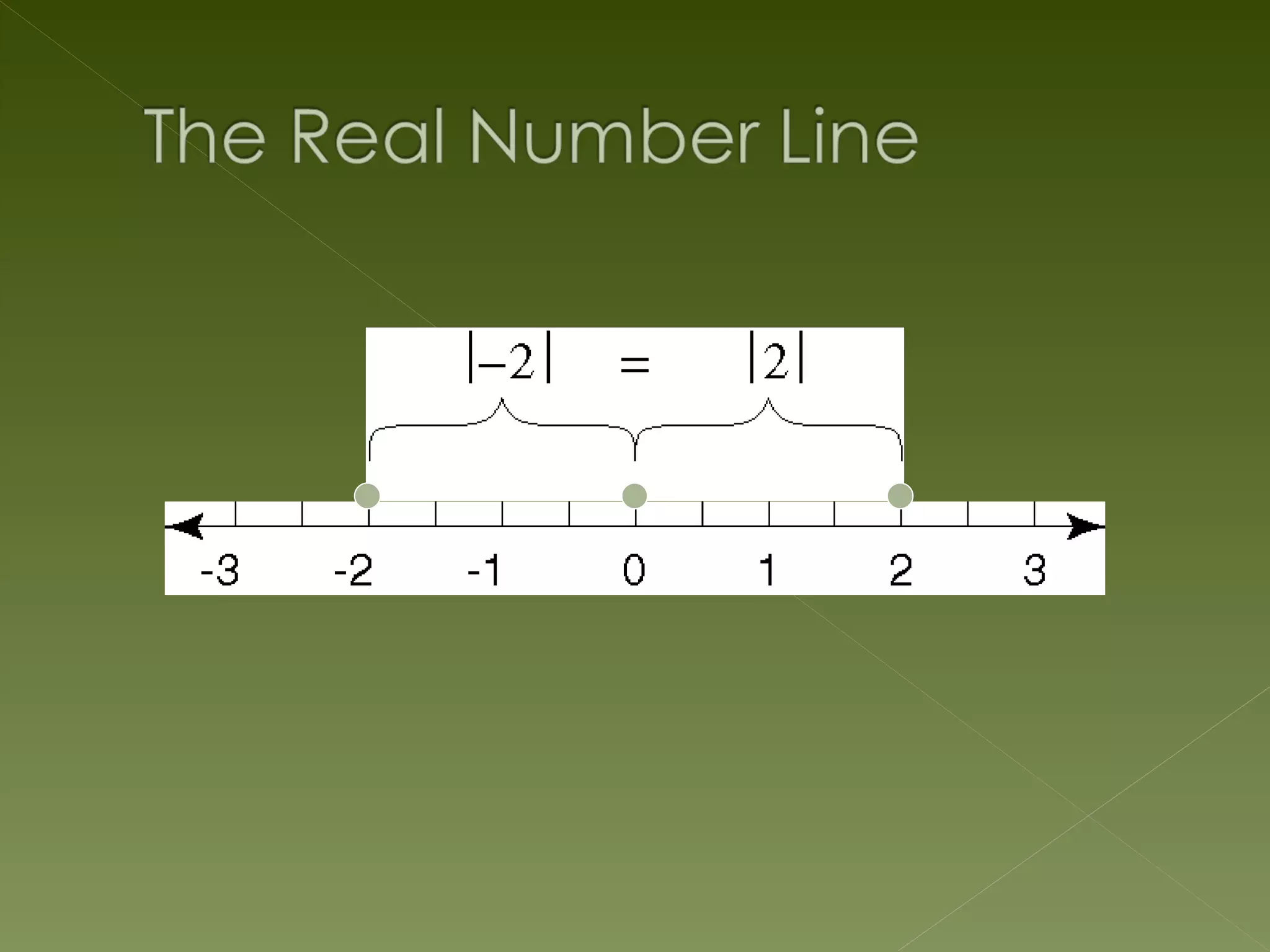
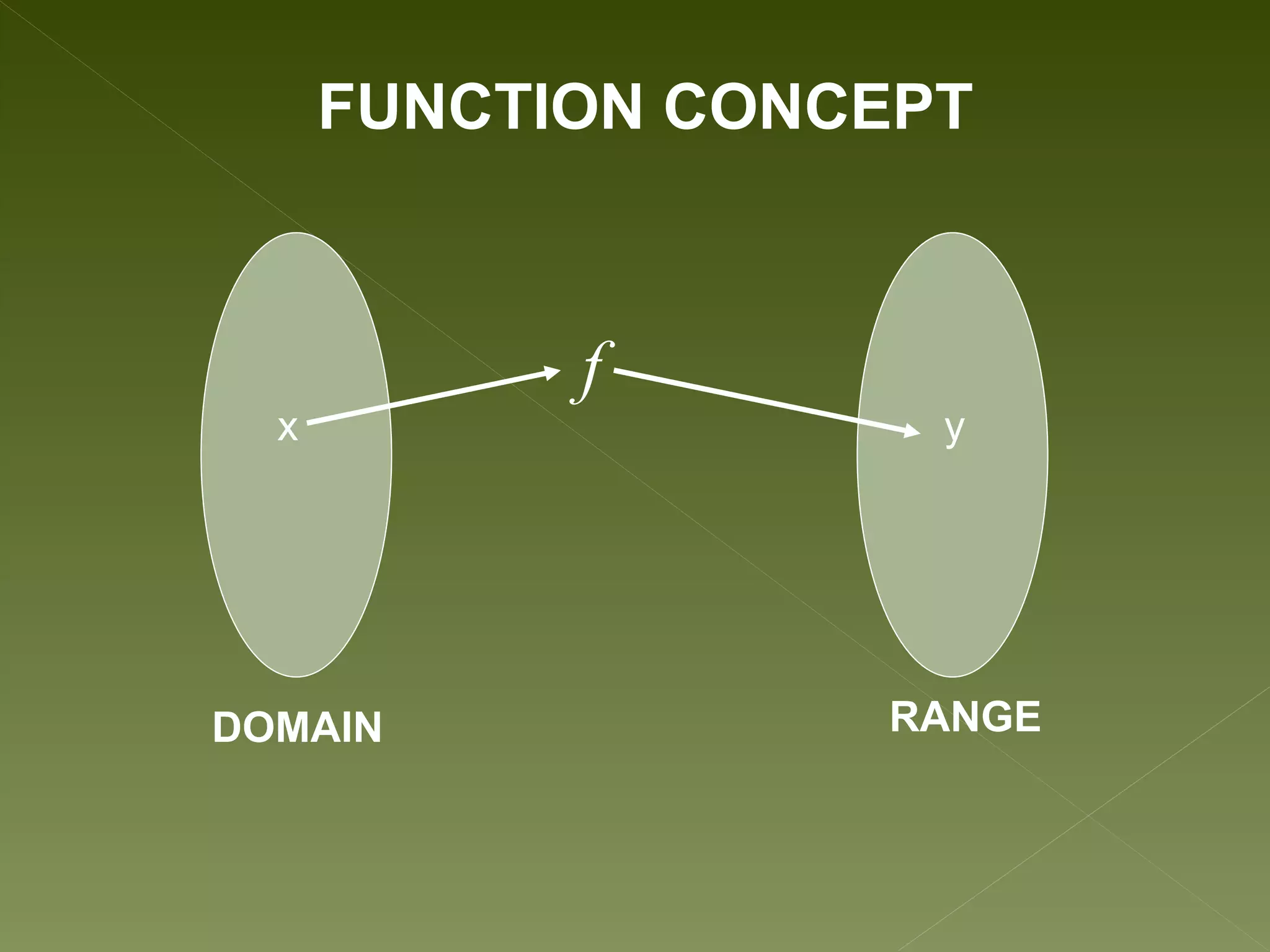
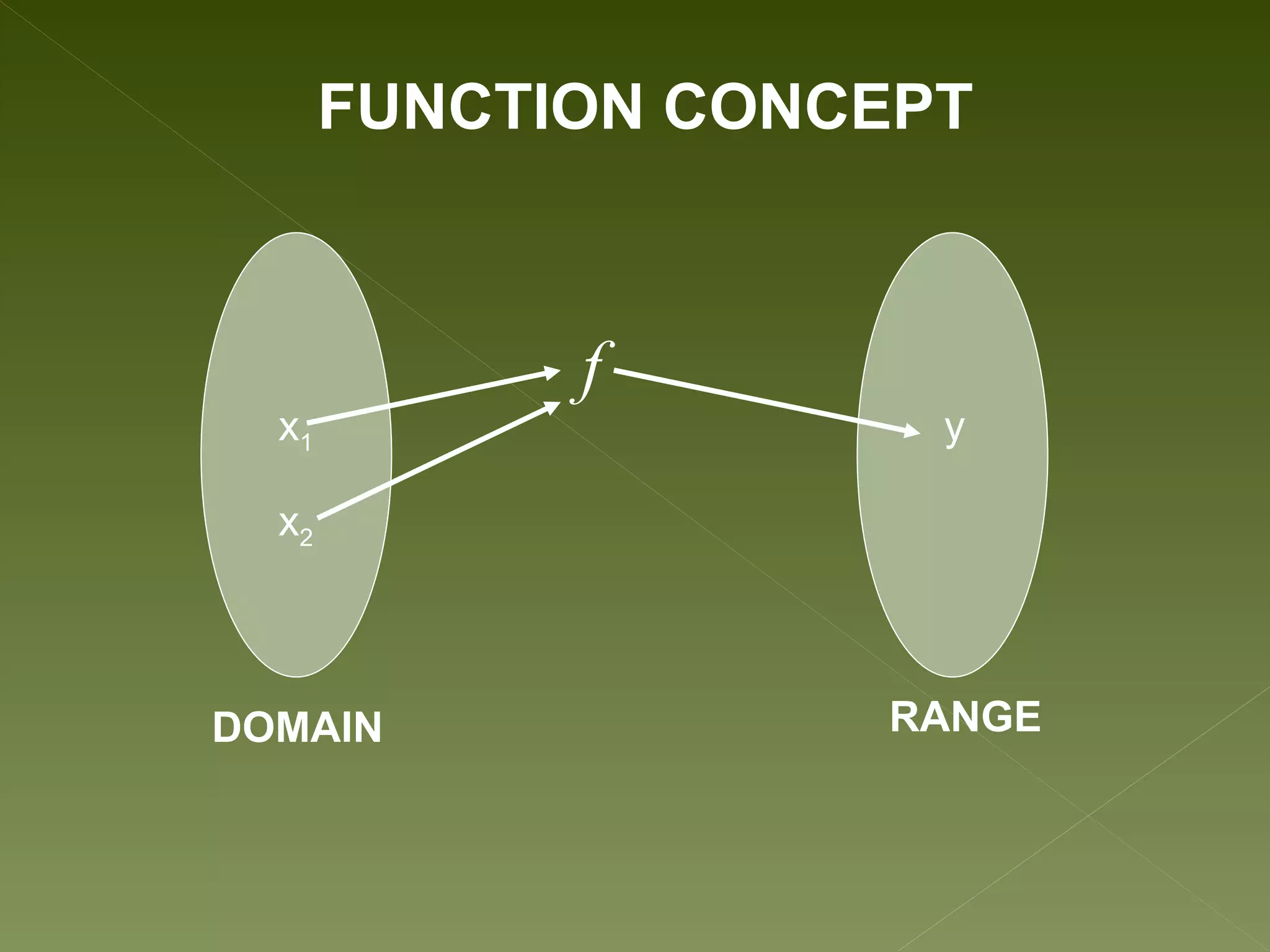
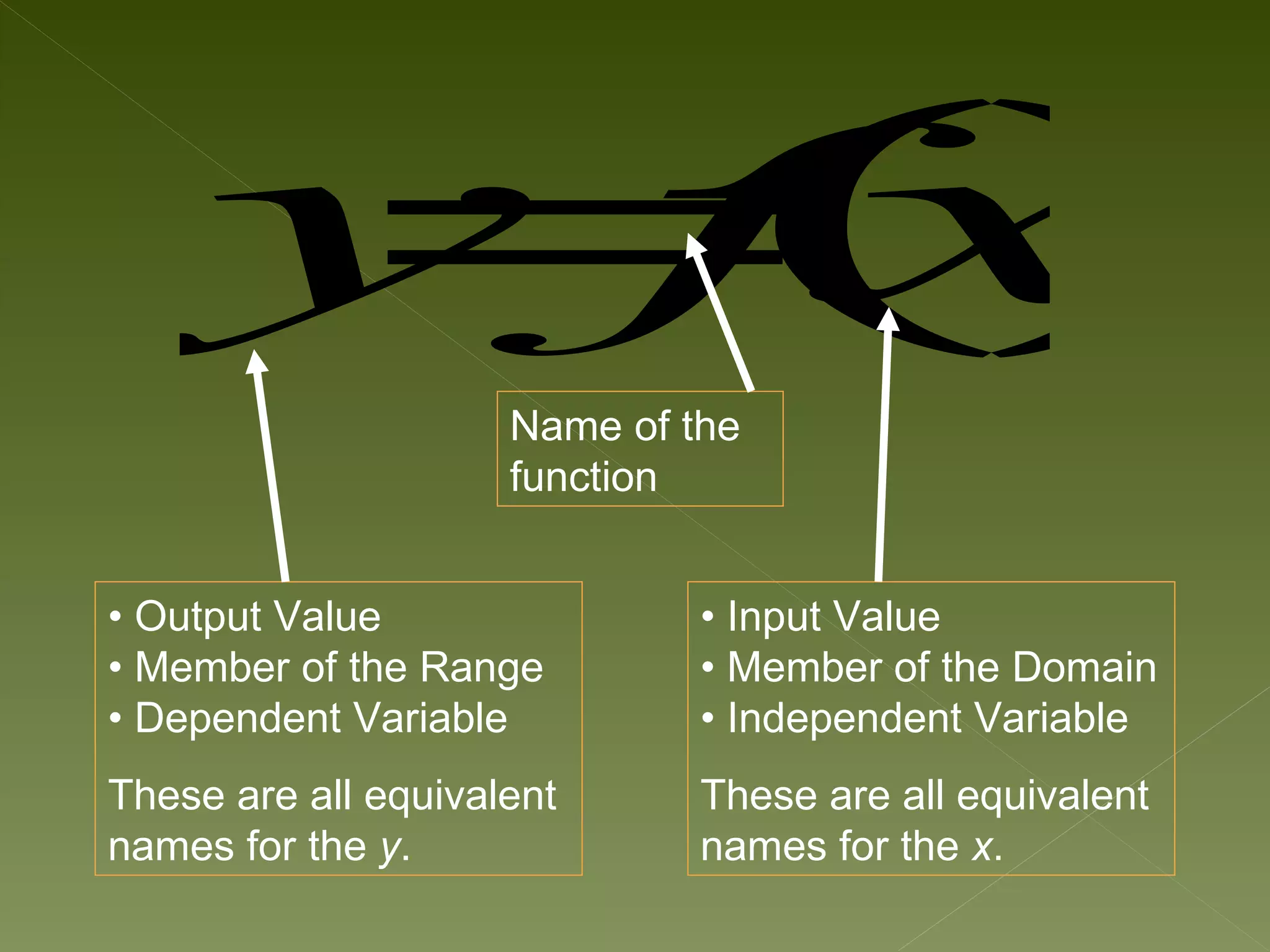
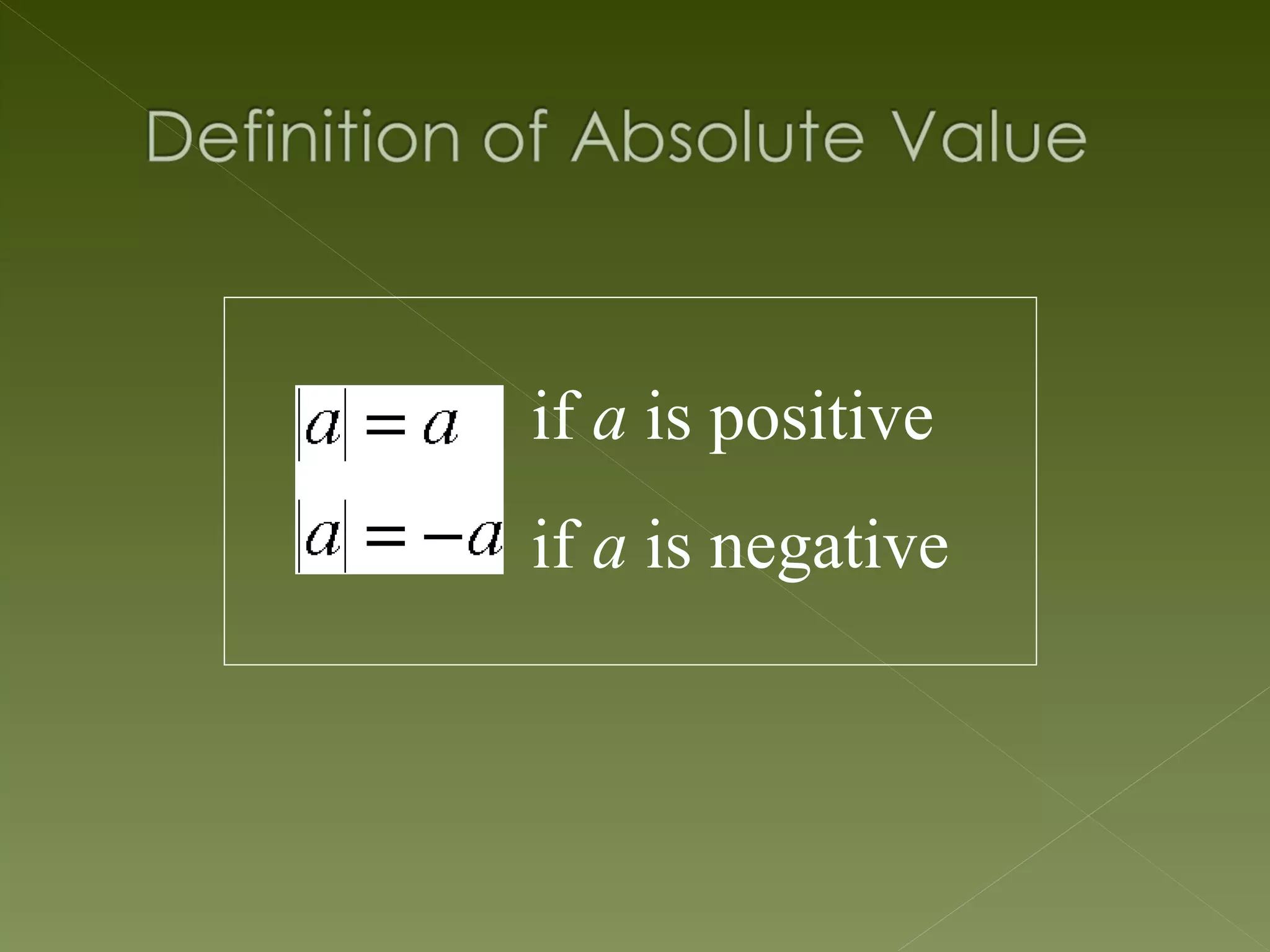The document discusses relations and functions. It defines relations as mappings between a domain and range, and functions as special relations where each domain element maps to only one range element. It provides examples of different representations of relations and functions, such as numeric, graphical, symbolic and verbal. Common types of functions in algebra are described as mapping subsets of real numbers to other subsets of real numbers. The key characteristics of functions and relations are summarized.

3. (A)
(B)
(C) ° 32 mpg
° 8 mpg
° 16 mpg

4.  The values that make up the set of
independent values are the domain
 The values that make up the set of
dependent values are the range.
 State the domain and range from the 4
examples of relations given.

7.  Transitive:
If a = b and b = c then a = c
 Identity:
a + 0 = a, a • 1 = a
 Commutative:
a + b = b + a, a • b = b • a
 Associative:
(a + b) + c = a + (b + c)
(a • b) • c = a • (b • c)
 Distributive:
a(b + c) = ab + ac
a(b - c) = ab - ac

8. if a is positive
if a is negative

11.  A Relation maps a value from the
domain to the range. A Relation is a set
of ordered pairs.
 The most common types of relations in
algebra map subsets of real numbers to
other subsets of real numbers.

12. Domain Range This is often referred to
as a diagrammatic
representation of a
3 π
relation. Note that each
element in the domain is
11 -2 connect to it’s
respective range
1.618 2.718 element by the arrow.

13.  The relation is the year and the cost of a
first class stamp.
 The relation is the weight of an animal
and the beats per minute of it’s heart.
 The relation is the time of the day and
the intensity of the sun light.
 The relation is a number and it’s square.

14.  If a relation has the additional
characteristic that each element of the
domain is mapped to one and only one
element of the range then we call the
relation a Function.

15. FUNCTION CONCEPT
f
x y
DOMAIN RANGE

16. NOT A FUNCTION
R
x y1
y2
DOMAIN RANGE

17. FUNCTION CONCEPT
f
x1 y
x2
DOMAIN RANGE

18.  Symbolic • Graphical
{x )y=2 }
( ,y x
or
y=2 x
• Numeric X Y
1 2
5 10 • Verbal
The cost is twice
-1 -2 the original
3 6 amount.

19.  A truly excellent notation. It is concise
and useful.
= ()
y fx

20. = ()
y fx
Name of the
function
• Output Value • Input Value
• Member of the Range • Member of the Domain
• Dependent Variable • Independent Variable
These are all equivalent These are all equivalent
names for the y. names for the x.

21.  The f notation
f( ) x 1
x= +
f( ) () 1
2 = 2+