1) The document is a lecture on transverse loading on beams and stresses in beams. It covers beam types, shear force and bending moment diagrams, stresses due to bending and shear, and analysis of determinate beams.
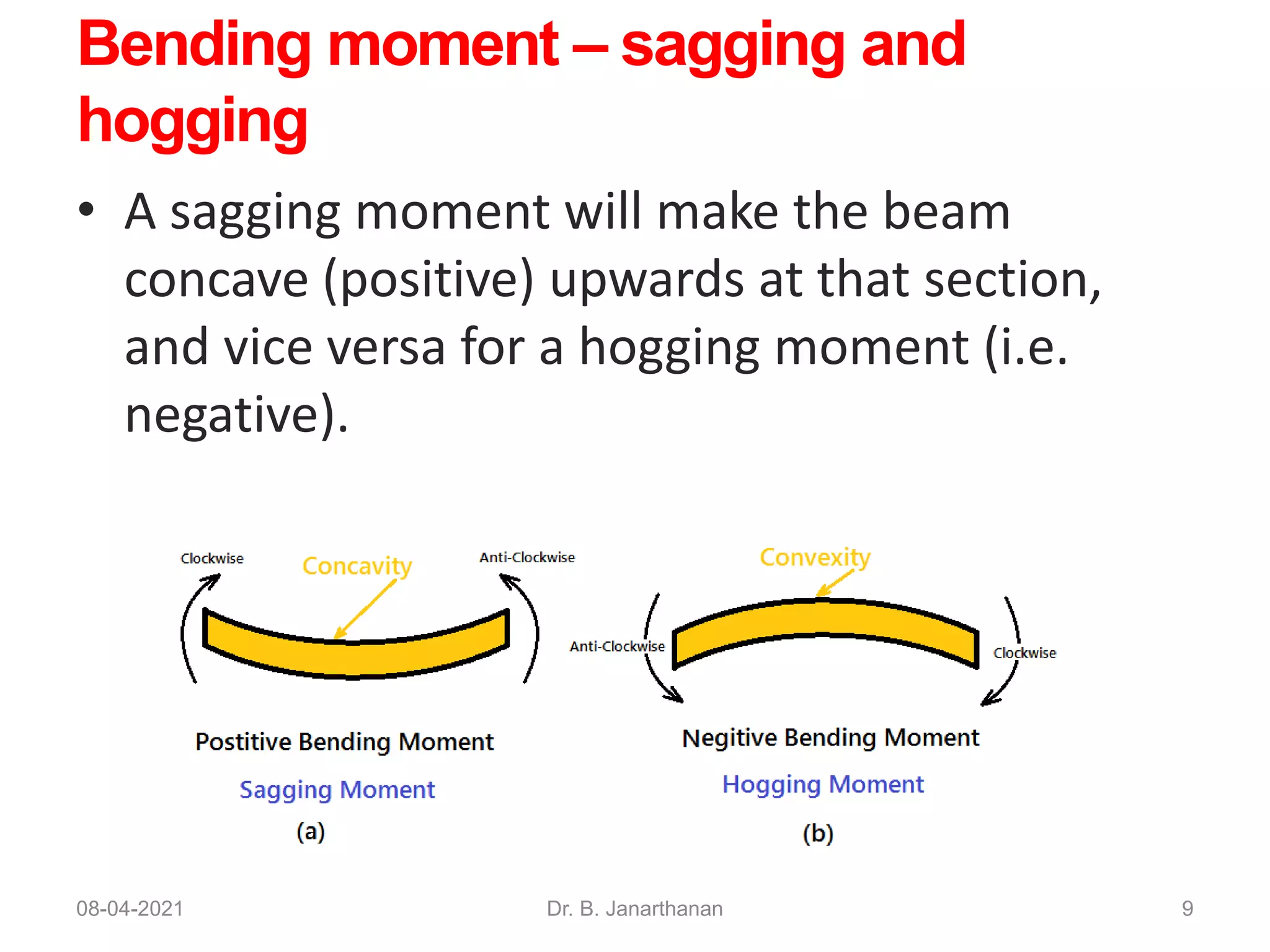
2) The lecture defines key concepts like shear force, bending moment, sagging and hogging moments. It demonstrates calculation of bending stresses and shear stresses in beams.
3) Various beam examples are presented including cantilever beams, simply supported beams, overhanging beams, and composite beams. Bending stresses are calculated for different beam loadings and sections.