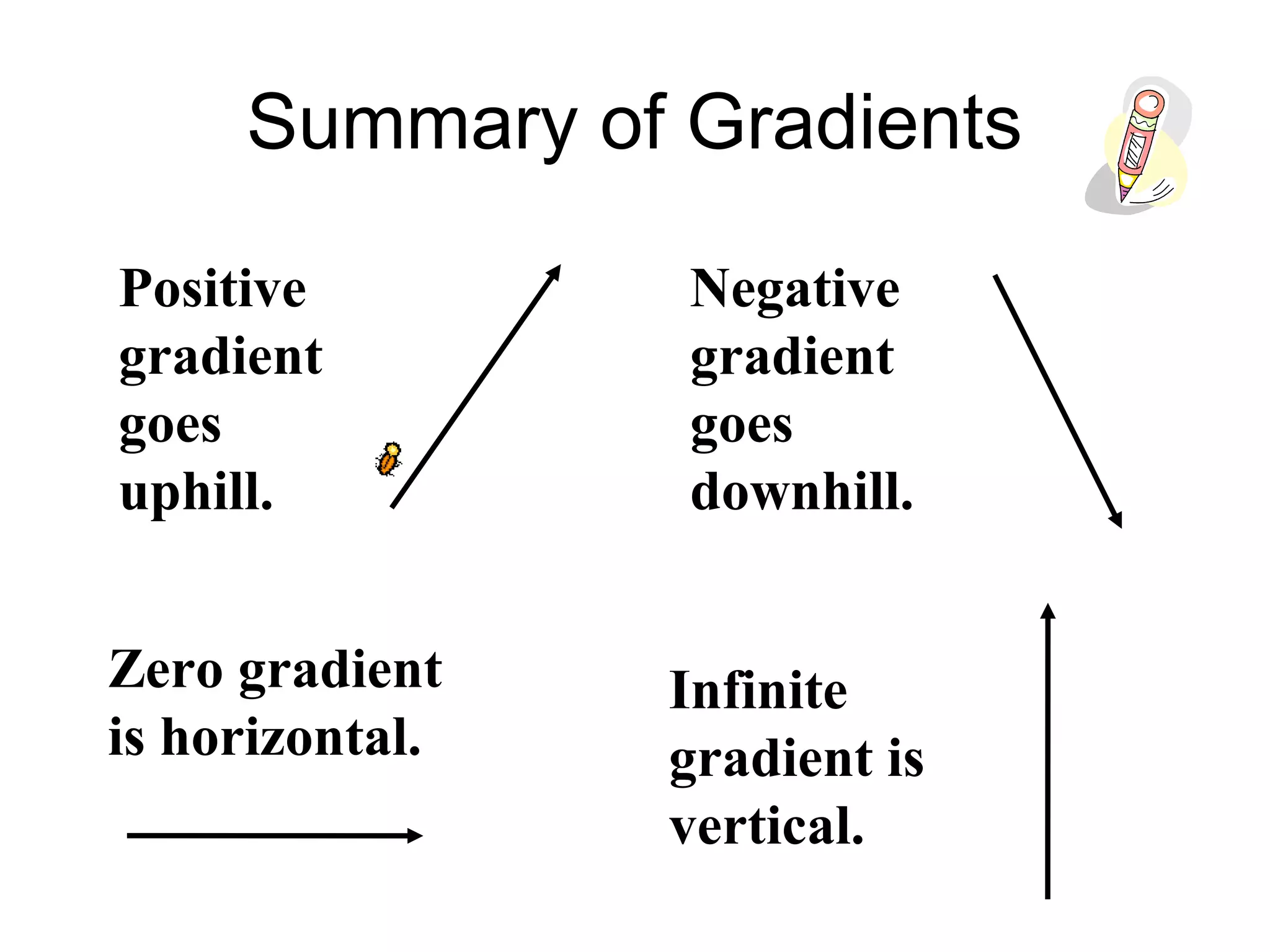
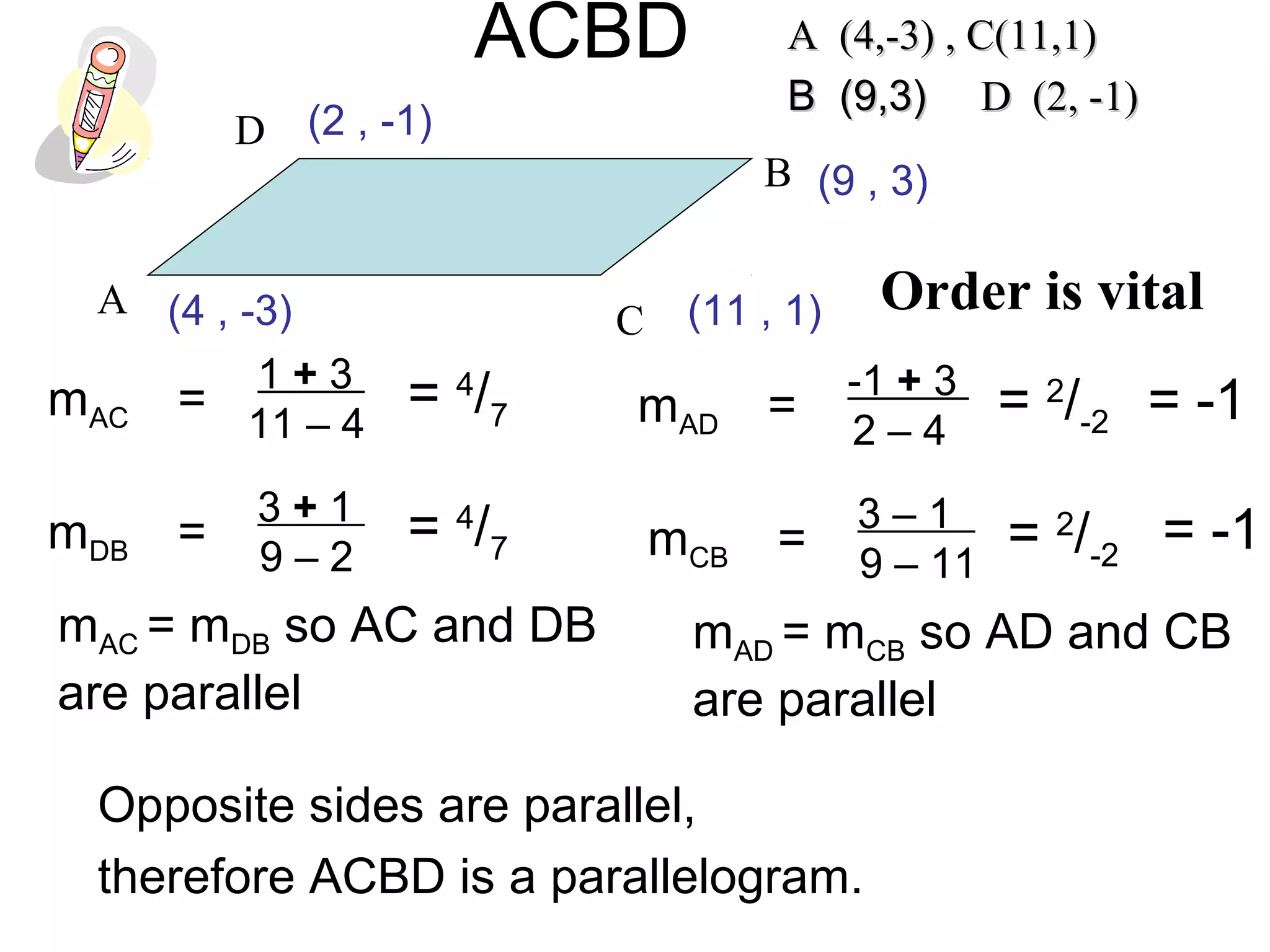
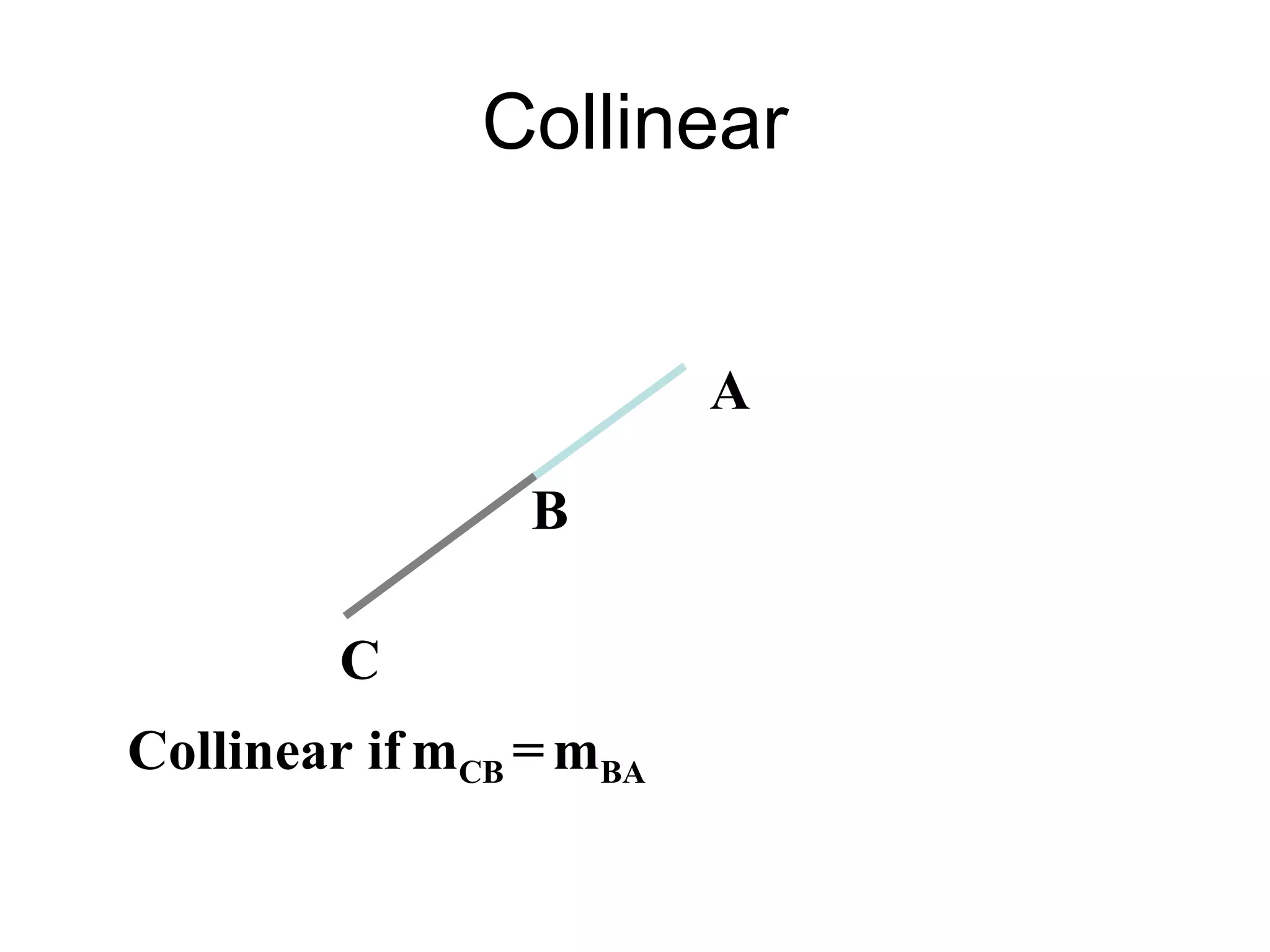
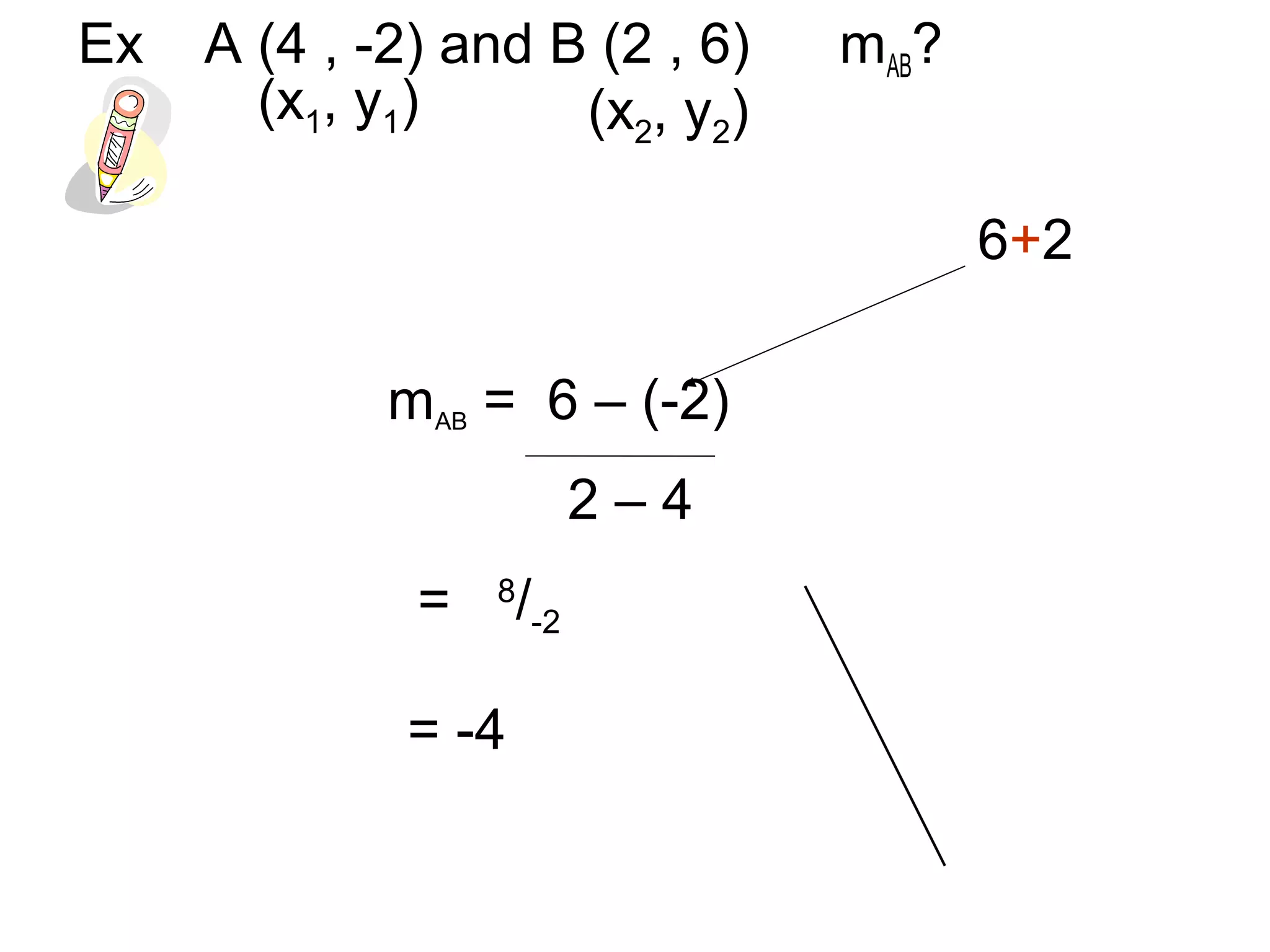The document discusses gradients and the gradient formula. It provides examples of calculating gradients between two points and identifying properties of gradients such as positive gradients going uphill and negative gradients going downhill. It then discusses applications of gradients including using equal gradients to prove that two lines are parallel and using equal gradients between three points to show they are collinear, or located on the same straight line.

1. Block 1
Gradient Formula

2. What is to be learned?
• How to use the gradient formula to
calculate gradients
• How to use gradients to identify shapes.

3. The Gradient Formula
m = y2 – y1
x2 – x1

4. The Gradient Formula
m = y2 – y1
x2 – x1

5. The Gradient Formula
m = y2 – y1
x2 – x1
Don’t let your ironing
board collapse!

6. Ex A (4 , -2) and B (2 , 6) mAB?
mAB = 6 – (-2)
(x1, y1) (x2, y2)
= 8
/-2
= -4
6+2
2 – 4

7. Summary of Gradients
Positive
gradient
goes
uphill.
Negative
gradient
goes
downhill.
Zero gradient
is horizontal.
Infinite
gradient is
vertical.

8. Parallel Lines
Parallel lines run in the same direction so
must be equally steep.
Hence parallel lines have equal gradients.
Example
Prove that if A is (4,-3) , B is (9,3)
C is (11,1) & D is (2, -1)
then ACBD is a parallelogram

9. ACBD
Opposite sides are parallel,
therefore ACBD is a parallelogram.
A
C
B
D
Order is vital
A (4,-3) , C(11,1)A (4,-3) , C(11,1)
B (9,3)B (9,3) D (2, -1)D (2, -1)
(4 , -3) (11 , 1)
(9 , 3)
(2 , -1)
mAC =
1 + 3
11 – 4
= 4
/7
mDB =
3 + 1
9 – 2
= 4
/7
mAC = mDB so AC and DB
are parallel
mAD =
-1 + 3
2 – 4
= 2
/-2
mCB =
3 – 1
9 – 11
= 2
/-2
mAD = mCB so AD and CB
are parallel
= -1
= -1

10. Collinear
C
B
A
Collinear if mCB =mBA

11. COLLINEARITY
Defn: Three or more points are said to be collinear if the
gradients from any one point to all the others is always
the same. _ They are in a straight line
K is (5, -8), L is (-2, 6) and M is (9, -16). Prove that the three
points are collinear.
mKL =
6 - (-8)
-2 - 5
=
14
-7
= -2
mKM =
-16 - (-8)
9 - 5
=
-8
4
= -2
Since KL & KM have
equal gradients and a
common point K then
it follows that K, L &
M are collinear.
points in a straight line → equal gradients

12. Need in a straight line

13. Achieved if
There is a Collinear
It’s what
I do

14. A Navy jet flies over two lighthouses with
map coordinates (210,115) & (50,35). If it
continues on the same path will it pass over
a yacht at (10,15) ?
m1 = (115-35)
/(210-50) = 80
/160 = 1
/2
m2 = (115-15)
/(210-10) = 100
/200 = 1
/2
Since gradients equal & (210,115) a common point
then the three places are collinear so plane must fly
over all three.