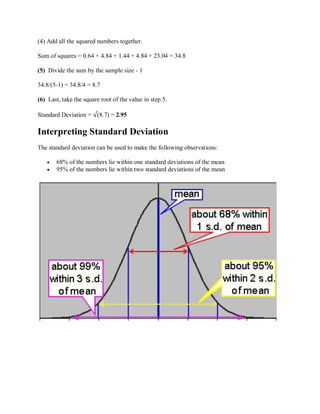
This document provides an introduction to key statistical concepts for biology, including mean, mode, median, and standard deviation. It defines sample size and population, and gives examples of calculating each statistical measure using a sample of movie ratings from 5 friends. The mean is the average, the mode is the most frequent value, the median is the middle value when numbers are ordered, and the standard deviation measures how spread out values are from the mean.

1. INTRODUCTION TO STATISTICS FOR BIOLOGY
In statistics, the most important calculations are the mean, mode, median, and standard
deviation.
Consider the following:
· sample size
· population
· mean
· mode
· median
· standard deviation
Sample Size and Population
Statistics begins with a set of numbers which are called the sample.
The set of all possible numbers is called the population.
Let's say that we ask 5 friends to rate a popular movie on the scale from 1 to 10.
Then, the sample size is 5 and the population is the set of all people who have seen or will see the
movie.
Calculating the mean
So, we ask our 5 friends to rate the movie and here's what we get:
Andreas: 6
Pantelina: 9
Michael: 8
Constantinos: 9
Lydia: 2
To calculate the mean, you sum up all the numbers in the sample and then divide by the sample
size. The sum is 5 + 10 + 8 + 9 + 2 = 34. Since the sample size is 5, the mean is 34/5 = 6.8
This then is the average of the sample.

2. Calculating the mode
The mode is the number that appears the most often in the sample.
To calculate the mode, we count the number of times each rating is made. So we have one 6, two
9's, one 8, and one 2. Since we have two 9's and one of everything else, 9 is the mode.
But what would happen if we have the following sequence: 2, 2, 8, 9, 9?
In this case, we would say that there is no unique mode. A mode is unique if and only if one
number is more frequent than all others.
Calculating the median
The median is the value we get when we order all of our numbers and then find the one in the
middle.
If we order the numbers from smallest to largest, we get: 2, 6, 8, 9, 9
Since we have a sample size of 5, the number in the middle is 8.
What happens if the sample size is even? We can add the two middle numbers and divide by 2.
So, if our numbers are: 2,6,8,9, then the median is (6+8)/2 = 7.
Calculating the Standard Deviation
The standard deviation is a measure of the variation of the sample data from the mean value. The
larger the s.d., the more the variation. Small s.d.means small variation.
Here are the steps to calculate standard deviation (normally you would use excel to work it out, it
is much easier and faster):
(1) Calculate the mean. This is the sum of the numbers given divided by the sample size (i.e. the
average).
(6 + 9 + 8 + 9 + 2) / 5 = 34/5 = 6.8
(2) Subtract the mean value from each of the measured values.
(6 - 6.8), (9 - 6.8), (8 - 6.8), (9 - 6.8), (2 - 6.8) = - 0.8, 2.2, 1.2, 2.2, - 4.8
(3) Square all numbers (to make the negative ones positive).
(-0.8)x(-0.8), (2.2)x(2.2), (1.2)x(1.2), (2.2)x(2.2), (-4.8)x(-4.8) = 0.64, 4.84, 1.44, 4.84, 23.04

3. (4) Add all the squared numbers together.
Sum of squares = 0.64 + 4.84 + 1.44 + 4.84 + 23.04 = 34.8
(5) Divide the sum by the sample size - 1
34.8/(5-1) = 34.8/4 = 8.7
(6) Last, take the square root of the value in step 5.
Standard Deviation = √(8.7) = 2.95
Interpreting Standard Deviation
The standard deviation can be used to make the following observations:
· 68% of the numbers lie within one standard deviations of the mean
· 95% of the numbers lie within two standard deviations of the mean