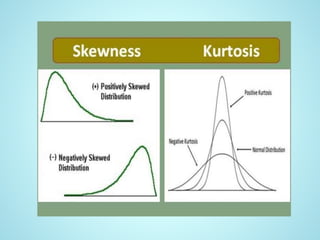
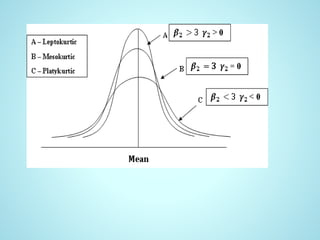
This document defines and explains skewness and kurtosis. Skewness refers to asymmetry in a bell curve distribution, with positive skewness meaning the curve is shifted right and negative skewness meaning it is shifted left. Kurtosis measures the tails of a distribution compared to a normal bell curve, with leptokurtic distributions having heavier tails and platykurtic having lighter tails. There are three categories of kurtosis - mesokurtic resembling a normal curve, leptokurtic with greater extremes, and platykurtic with shorter broader tails.

1. SKEWNESS AND KURTOSIS
Mrs.P.Kalaiselvi M.Sc.,M.A.
Miss.S.Swathi Sundari M.Sc.M.Phil.

6. What Is Skewness?
 Skewness refers to distortion or asymmetry in a
symmetrical bell curve, or normal distribution, in a
set of data. If the curve is shifted to the left or to the
right, it is said to be skewed.
 Skewness can be quantified as a representation of
the extent to which a given distribution varies from a
normal distribution. A normal distribution has a skew
of zero.
 The three probability distributions depicted below are
positively-skewed (or right-skewed) to an increasing
degree. Negatively-skewed distributions are also
known as left-skewed distributions.

9. DEFINITION of Kurtosis
 Like skewness, kurtosis is a statistical measure
that is used to describe the distribution. Whereas
skewness differentiates extreme values in one
versus the other tail, kurtosis measures extreme
values in either tail.
 Kurtosis is a measure that describes the shape of
a distribution's tails in relation to its overall
shape. A distribution can be infinitely peaked
with low kurtosis, and a distribution can be
perfectly flat-topped with infinite kurtosis. Thus,
kurtosis measures “tailedness,” not “peakedness.”

10.  There are three categories of kurtosis that can be
displayed by a set of data. All measures of kurtosis are
compared against a standard normal distribution, or bell
curve.
 The first category of kurtosis is a mesokurtic distribution.
This distribution has kurtosis statistic similar to that of the
normal distribution, meaning that the extreme value
characteristic of the distribution is similar to that of a
normal distribution.
 The second category is a leptokurtic distribution. Any
distribution that is leptokurtic displays greater kurtosis
than a mesokurtic distribution.
 The final type of distribution is a platykurtic distribution.
These types of distributions have short tails .The prefix of
"platy-" means "broad," and it is meant to describe a short
and broad-looking peak.

14.  THANK YOU