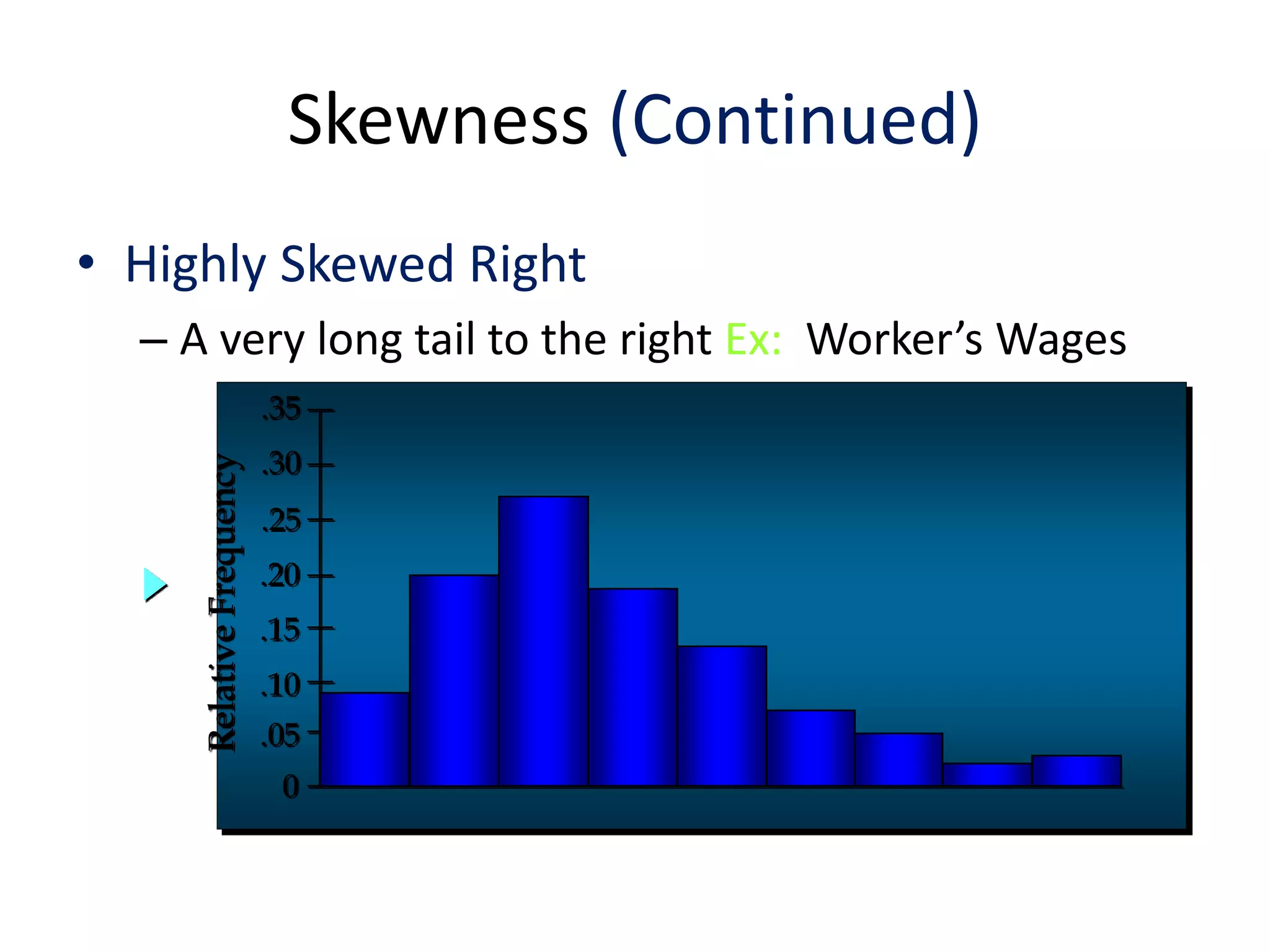
This document discusses skewness and kurtosis, which are measures of the shape of a statistical distribution. Skewness measures symmetry and describes how far the tails are from the mean. Kurtosis measures whether the distribution is heavy or light tailed versus a normal distribution. Examples of skewed distributions from various fields are given. Applications of skewness and kurtosis include identifying outliers and determining the normality of distributions in areas like insurance claims.

1. Skewness & Kurtosis
Dr. S. Doss

2. Measures of Shape
• Symmetrical – the right half is a mirror image
of the left half
• Skewed – shows that the distribution lacks
symmetry; Absence of symmetry
– Extreme values or “tail” in one side of a distribution
– Positively- or right-skewed vs. negatively- or left-
skewed

3. Coefficient of Skewness
 

 d
M
Sk


3
• Coefficient of Skewness (Sk)- compares the mean
and median in light of the magnitude to the
standard deviation; Md is the median; Sk is
coefficient of skewness; σ is the Std Dev

4. Coefficient of Skewness
• Summary measure for skewness
• If Sk < 0, the distribution is negatively skewed (skewed to
the left).
• If Sk = 0, the distribution is symmetric (not skewed). If Sk
is close to 0, it’s almost symmetric
• If Sk > 0, the distribution is positively skewed (skewed to
the right).
 

 d
k
M
S


3

5. • Symmetric Left tail is the mirror image of the
right tail. Example: heights and weights of
people
Histogram
Relative
Frequency
.05
.10
.15
.20
.25
.30
.35
0

6. • Moderately Skewed Left
– A longer tail to the left Example: Exam scores
Relative
Frequency
.05
.10
.15
.20
.25
.30
.35
0
Skewness (Continued)

7. • Moderately Right Skewed
– A Longer tail to the right Example: Housing values
Relative
Frequency
.05
.10
.15
.20
.25
.30
.35
0
Skewness (Continued)

8. • Highly Skewed Right
– A very long tail to the right Ex: Worker’s Wages
Relative
Frequency
.05
.10
.15
.20
.25
.30
.35
0
Skewness (Continued)

9. Positions of Mean, Median and Mode
in Left and Right Skewed Distributions

10. Applications of Skewness
• No of wealthy people in USA
• Economically poor people in Somalia (Africa)
• Cricket Scores by top batsman (80:20)
• Movie Ticket sales of popular Actor
• Skewness in model building
• It helps in identifying the outliers
• Mode > Median > Mean – Identify distribution
• Mean > Median > Mode – Identify distribution

11. • The positive excess value will have peaked curve
(Leptokurtic)
• The negative excess value will have a flat curve
(Platykurtic)
• The normal distribution will have an excess k value
of ‘0’ (K-3 = 0) or kurtosis value of 3 (k=3).

12. Leptokurtic Distribution
• Leptokurtic distribution will have high values of K or Excess positive
values of K (B2 -3 = 6).
• It will have high frequency of moderate values and also
comparatively large values as compared to normal distribution.
• The tail of the distribution will be comparatively thicker.

13. Platykurtic Distribution
• Platykurtic distribution will have lower values of K or Excess negative
values of K (B2 -3 = -1).
• It will have larger values of small and moderate values with wider
volatility as the standard deviation is expected to be comparatively
larger.
• The tail of the distribution will be comparatively lighter.

14. Applications of Kurtosis
• Leptokurtic distribution in General Insurance
– High Frequency claims with moderate severity – Motor
Insurance accident claims in rainy season, Crop Insurance
in drought, Health Insurance during pandemic.
• Mesokurtic distribution
– Property claims of householders, marine cargo claims, Fire
Claims, etc.
• Platykurtic distribution
– Property claims of shopkeepers, textile, machinery,
fertilizer sectors.
– TP claims of commercial vehicles
– Motor accident claims of private cars including luxury
vehicles
– Flood claims

15. Applications of Kurtosis
• Helpful to decide the normality of distribution
• Measures the peak as well as thickness of the
tail.
• Higher value indicates larger the risk as the tail
is thicker.
• Thicker the tail indicates extreme values or
losses.
• Lower the kurtosis value indicates lesser freq
of high value losses.