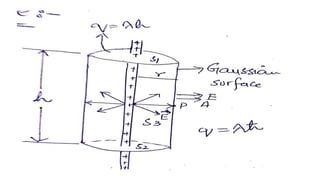
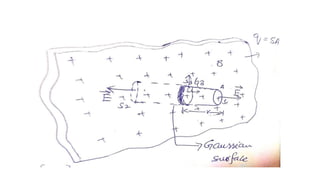
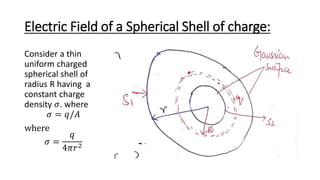
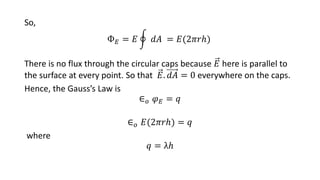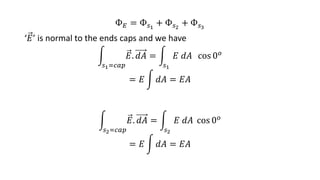- Gauss's law provides a simpler way to calculate electric fields (E-fields) in situations with a high degree of symmetry by relating the electric flux through a closed surface to the net charge enclosed. - The electric flux (ΦE) is defined as the number of electric field lines passing through a surface element and depends on the angle between the E-field and surface area vectors. - According to Gauss's law, the total electric flux through any closed surface is equal to 1/ε0 times the net charge enclosed; this relationship can be used to deduce Coulomb's law and calculate E-fields for symmetric charge distributions like infinite lines/sheets of charge and spherical shells.

1. Chapter 3

2. Introduction to Gauss’s Law:
• Gauss’s law provide us another way to calculate E.F. It offers simpler
way to calculate E.F in situations with a high degree of symmetry.
• We first need to define ‘Flux of Electric Field’ that is a mathematical
property of any field represented by vectors that is determined by
surface integral of the field vector over a particular area.
• Vector Area is ‘ normal to any flat surface’
𝑑𝐴 = 𝑑𝐴. 𝑛
Vector area is a vector quantity whose magnitude is equal to area of
surface element and direction is always along the outward drawn
normal to the center of surface element.

3. Flux means flow, derived from Latin word.
Flux is a measure of field lines passing through the loop/ surface
element.
Electric Flux:
“ The number of field lines passing through a certain area
element ‘A’ called flux of Electric Field and represented by
Ф𝐸 = 𝐸 ∙ 𝐴
Electric Flux is a scalar and units are𝑁𝑚2
𝐶.

4. It depends upon angle formed b/w Electric field vector 𝐸 and surface
area 𝐴.
• For 𝜃 = 0𝑜 , Ф𝐸 will be maximum.
• For 𝜃 = 90𝑜
, Ф𝐸 will be minimum and for 𝜃 = 180𝑜
, Ф𝐸 gives –ve
maximum value.
• Gauss’s Law deals with flux of a closed surface. If E.Field is not
uniform over the vector area, then we divide the whole surface into
large number of small elements. Then
Ф𝐸 =
𝑠
𝐸 ∙ 𝑑𝐴

5. • For closed surface,
Ф𝐸 = 𝐸 ∙ 𝑑𝐴
By convention, outward flux is taken as +ve and inward flux is taken as
–ve.
The Electric field over a closed surface is
i. Zero, if surface encloses no charge.
ii. Positive and equal in magnitude to their strength, if surface
contains only +ve charges.
iii. Negative and equal in magnitude to their strength, if surface
contains only -ve charges.
iv. Zero, if surface contains equal no. of +ve and –ve charges.

6. Gauss’s Law:
The total Electric Flux through a closed surface is equal to
1
∈𝑜
times the
net charge enclosed by the closed surface.
𝜑𝐸 =
1
∈𝑜
𝑞
Or
∈𝑜 𝜑𝐸 = 𝑞
Or
∈𝑜 𝐸 ∙ 𝑑𝐴 = 𝑞
Gauss’s law predicts that 𝜑𝐸 is zero for closed surfaces bcz surface encloses
no charge.

7. Gauss’s Law for a point charge enclosed by a
surface:
Consider a point charge ‘q’ inside a closed surface ‘s’ of any shape.
Divide the surface into large number of small patches such that surface
over each patch is practically flat.
Consider one patch of vector area 𝑑𝐴 at point P. Let 𝑟 be the position
vector of P w.r.t ‘O’ where charge ‘q’ lies. Then Electric Field at point P
due to charge ‘q’ is
𝐸 =
1
4𝜋𝜖𝑜
𝑞
𝑟2
𝑟
Where 𝑟 is unit vector directed from O to P.

8. Then Electric Flux through 𝑑𝐴 is
𝑑Ф𝐸 = 𝐸 ∙ 𝑑𝐴
𝑑Ф𝐸 = 𝐸 ∙ 𝑛𝑑𝐴
Where 𝑛 is unit vector drawn outward normal to 𝑑𝐴 , then Electric Flux
through whole surface is
Ф𝐸 = 𝐸 ∙ 𝑛𝑑𝐴
By substituting value of 𝐸 is
Ф𝐸 =
1
4𝜋𝜖𝑜
𝑞
𝑟2
𝑟 ∙ 𝑛𝑑𝐴

9. Ф𝐸 =
𝑞
4𝜋𝜖𝑜
𝑟 ∙ 𝑛
𝑟2
𝑑𝐴
∴ 𝑠𝑜𝑙𝑖𝑑 𝑎𝑛𝑔𝑙𝑒 =
𝑟∙𝑛
𝑟2 𝑑𝐴 = 4π
Ф𝐸 =
𝑞
4𝜋𝜖𝑜
(4π)
Ф𝐸 =
𝑞
𝜖𝑜
So,
𝜖𝑜Ф𝐸 = 𝑞
Which is prove of Gauss’s Law.

10. Gauss’s Law and Coulomb’s Law:
• To deduce Coulomb’s law from Gauss’s law, let us apply Gauss’s Law
to an isolated positive charge q. Gauss’s Law holds for any surface. So,
we choose a spherical surface (Gaussian surface) of radius ‘r’
centered on charge.
• Electric field 𝐸 must be perpendicular to the surface. 𝐴 is the vector
area of the Gaussian surface. We divide the whole surface into large
number of small elements d𝐴. So, the angle ′𝜃′ b/w 𝐸 and d𝐴 is zero
everywhere on the surface and 𝐸 has same magnitude everywhere
on surface. Both 𝐸 and d𝐴 at any point on the Gaussian surface are
directed radially outward. So, the quantity 𝐸. d𝐴 becomes simply EdA.

11. So, Gauss’s Law reduces to
𝜖𝑜 𝐸 ∙ 𝑑𝐴 = 𝑞
𝜖𝑜 𝐸. 𝑑𝐴 = 𝑞
𝜖𝑜𝐸 𝑑𝐴 = 𝑞
∴ 𝑇𝑜𝑡𝑎𝑙 𝑠𝑢𝑟𝑓𝑎𝑐𝑒 𝑎𝑟𝑒𝑎 𝑜𝑓 𝑡ℎ𝑒 𝑠𝑝ℎ𝑒𝑟𝑒 = 𝑑𝐴 = 4𝜋𝑟2

12. So,
𝜖𝑜𝐸(4𝜋𝑟2) = 𝑞
𝐸 =
1
4𝜋𝜖𝑜
𝑞
𝑟2
Which is the magnitude of E.Field at any point a distance r from an
isolated point q, which was obtained fro Coulomb’s Law.
Gauss’s Law regarded as most fundamental equation of
Electromagnetism.

13. Application of Gauss’s Law:
• Gauss’s law can be used to calculate if symmetry of charge
distribution is high.

14. Infinite line of Charge:
• Consider an infinite line (wire) of charge of constant positive linear
charge density λ where
λ =
𝑞
ℎ
We have to find E.F at a distance ‘r’ from the line . Electric field is radial
and is independent to the position along the wire and angular position
around the wire and only depends upon the distance ‘r’ from the line
of charge.
For this purpose, we imagine a Gaussian surface in the form of circular
cylinder of radius ‘r’ and length ‘h’, closed at each end by plane caps
normal to the axis.

16. The E . Flux over the whole surface of cylinder is
Ф𝐸 = 𝐸. 𝑑𝐴
= 𝐸 𝑑𝐴 𝑐𝑜𝑠𝜃
= 𝐸 𝑑𝐴
‘E’ is constant over the cylindrical surface and perpendicular to surface.
∴ 𝑑𝐴 = 2𝜋𝑟ℎ

17. So,
Ф𝐸 = 𝐸 𝑑𝐴 = 𝐸(2𝜋𝑟ℎ)
There is no flux through the circular caps because 𝐸 here is parallel to
the surface at every point. So that 𝐸. 𝑑𝐴 = 0 everywhere on the caps.
Hence, the Gauss’s Law is
∈𝑜 𝜑𝐸 = 𝑞
∈𝑜 𝐸(2𝜋𝑟ℎ) = 𝑞
where
𝑞 = λℎ

18. ∈𝑜 𝐸(2𝜋𝑟ℎ) = λℎ
𝐸 =
λ
2𝜋 ∈𝑜 𝑟
𝐸 =
λ
2𝜋 ∈𝑜 𝑟
𝑟
Which is required expression.

19. Infinite Sheet of Charge:
Consider a portion of a thin, non-conducting, infinite sheet of charge of
constant positive surface charge density 𝜎 where
𝜎 = 𝑞/𝐴
The electric field 𝐸 produced perpendicular and away from the sheet.
We have to calculate E.F at points near the sheet.
Consider a Gaussian surface in the form of a closed cylinder of cross-
sectional area A passing normally through the sheet. Then
Ф𝐸 = 𝐸. 𝑑𝐴

21. Ф𝐸 = Ф𝑠1
+ Ф𝑠2
+ Ф𝑠3
‘𝐸’ is normal to the ends caps and we have
𝑠1=𝑐𝑎𝑝
𝐸. 𝑑𝐴 =
𝑠1
𝐸 𝑑𝐴 cos 0𝑜
= 𝐸 𝑑𝐴 = 𝐸𝐴
𝑠2=𝑐𝑎𝑝
𝐸. 𝑑𝐴 =
𝑠2
𝐸 𝑑𝐴 cos 0𝑜
= 𝐸 𝑑𝐴 = 𝐸𝐴

22. 𝑠3=𝑐𝑢𝑟𝑣𝑒𝑑
𝐸. 𝑑𝐴 =
𝑠3
𝐸 𝑑𝐴 cos 90𝑜
= 0
So total flux is
Ф𝐸 = Ф𝑠1
+ Ф𝑠2
+ Ф𝑠3
Ф𝐸 = 𝐸A + EA + 0
Ф𝐸 = 2𝐸A
So, Gauss’s Law gives
𝜑𝐸 =
1
∈𝑜
𝑞
Or
∈𝑜 𝜑𝐸 = 𝑞

23. Where
q = 𝜎𝐴
So,
∈𝑜 (2𝐸A) = 𝜎𝐴
𝐸 =
𝜎
2 ∈𝑜
In vector form,
𝐸 =
𝜎
2 ∈𝑜
𝑟

24. Electric Field of a Spherical Shell of charge:
Consider a thin
uniform charged
spherical shell of
radius R having a
constant charge
density 𝜎. where
𝜎 = 𝑞/𝐴
where
𝜎 =
𝑞
4𝜋𝑟2

25. For Electric Fields, The Shell Theorems stated below;
1. A uniform Spherical shell of charge behaves (like a point charge), for
external points, as if all its charge were concentrated as its center.
2. A uniform Spherical shell of charge exerts no electrical force on a
charged particle inside the shell.
To prove these Shell Theorem, Suppose that shell is surrounded by two
concentric spherical Gaussian surface 𝑆1for which 𝑟 > 𝑅 and 𝑆2for
which 𝑟 < R .

26. From a symmetry argument, we conclude that the field can have only a
radial component 𝐸𝑟 (along the radius). If 𝐸𝑟 is the E.F on Gaussian
surface 𝑆1, then total Electric flux through this surface is
Ф𝐸 =
𝑠1
𝐸𝑟. 𝑑𝐴
Ф𝐸 =
𝑠1
𝐸𝑟𝑑𝐴
Since 𝐸𝑟 has constant magnitude on 𝑆1 and along radius.
Ф𝐸 = 𝐸𝑟
𝑠1
𝑑𝐴

27. 𝑠1
𝑑𝐴 = 4𝜋𝑟2
Ф𝐸 = 𝐸𝑟(4𝜋𝑟2)
By Gauss’s Law, then
∈𝑜 𝜑𝐸 = 𝑞
∈𝑜 𝐸𝑟(4𝜋𝑟2) = 𝑞
𝐸𝑟 =
1
4𝜋 ∈𝑜
𝑞
𝑟2
For 𝑟 > 𝑅 .

28. Which gives the magnitude of E.Field on all the points on Gaussian
surface 𝑆1 having radius 𝑟 > 𝑅 .
This shows that uniformly charged shell behave like a point charge for
all points outside the shell. This proves the 1st Shell Theorem.
Now apply Gauss’s Law for surface 𝑆2 for which 𝑟 < R because
Gaussian surface 𝑆2 encloses no charge.
∈𝑜 𝜑𝐸 = 0
𝜑𝐸 = 0

29. Hence Gaussian surface encloses no charge and because 𝐸𝑟 has the
same value everywhere on surface. The Electric Field, therefore vanish
inside a uniform shell of charge; a test charge placed anywhere in the
interior would feel no electric force. This proves the second Shell
Theorem.
These Shell Theorem apply only for uniformly charged shell. If charges
were sprayed on the surface in a non-uniform manner, such that charge
density varied over the surface, these Theorems would not apply.