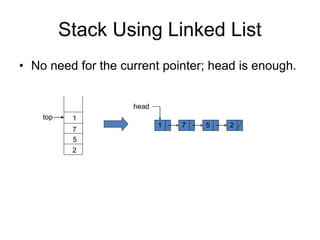
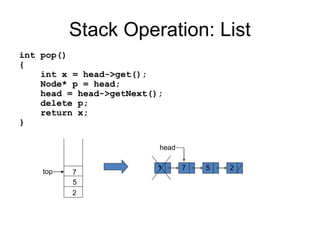
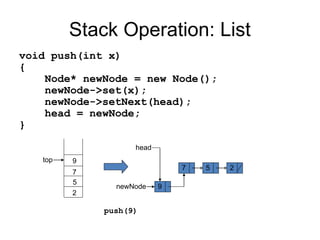
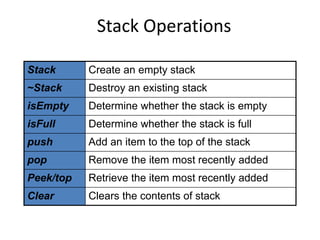
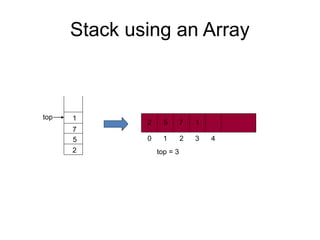
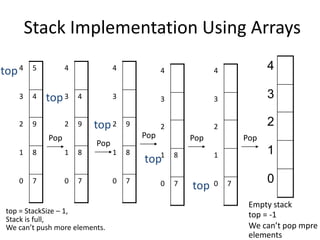
The document discusses abstract data types (ADTs) with a focus on stacks, defining their properties and operations like push, pop, and peek. It explains two implementations of stacks, through static arrays and dynamic linked lists, highlighting the advantages and limitations of each method. The document also covers real-life applications of stacks, as well as their use in evaluating expressions with a detailed explanation of infix, prefix, and postfix notations.







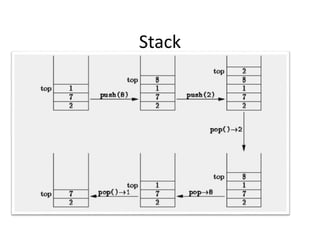





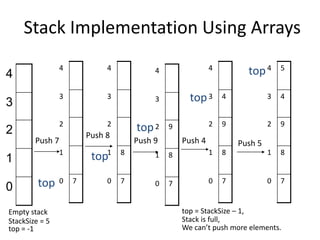
![Stack Implementation Using Arrays
push(element)
{
if (top == StackSize – 1)
cout<<“stack is full”;
else
Stack[++top] = element;
}](https://image.slidesharecdn.com/stackv-170125230621/85/Stack-in-Sata-Structure-19-320.jpg)
![Stack Implementation Using Arrays
pop()
{
if (top == –1)
cout<<“stack is empty”;
else
return Stack[top--];
}](https://image.slidesharecdn.com/stackv-170125230621/85/Stack-in-Sata-Structure-21-320.jpg)
![Stack Implementation Using Arrays
topElement() //returns the top element of stack
//without removing it.
{
if (top == –1)
cout<<“stack is empty”;
else
return Stack[top];
}](https://image.slidesharecdn.com/stackv-170125230621/85/Stack-in-Sata-Structure-22-320.jpg)


![Stack Implementation Using Arrays
//This constructor creates a stack.
Stack(unsigned int Max_Size)
{
Full_Stack = Max_Size;
Top_of_Stack = -1;
Stack_Array = new Element_Type[Max_Size];
}
/* This Destructor frees the dynamically allocated
space to the array */
~Stack()
{
delete Stack_Array;
}
Continue on next slide…](https://image.slidesharecdn.com/stackv-170125230621/85/Stack-in-Sata-Structure-25-320.jpg)

![Stack Implementation Using Arrays
// If stack is not full then push an element x in it
void Push(Element_Type x)
{ if(is_Full())
cout<<“stack is full”;
else
Stack_Array[++Top_of_Stack] = x;
}
//if Stack is not empty then pop an element form it
Element_Type pop()
{ if(is_Empty())
cout<<“stack is empty”;
else
return Stack_Array[Top_of_Stack--];
}
Continue on next slide…](https://image.slidesharecdn.com/stackv-170125230621/85/Stack-in-Sata-Structure-27-320.jpg)
![Stack Implementation Using Arrays
// This function makes the stack empty
void Make_Empty()
{ Top_of_Stack = -1;
}
/* This function returns the top element of stack */
Element_Type Top()
{
if(is_Empty())
cout<<“stack is emepty”;
else
return Stack_Array[Top_of_Stack];
}
};](https://image.slidesharecdn.com/stackv-170125230621/85/Stack-in-Sata-Structure-28-320.jpg)