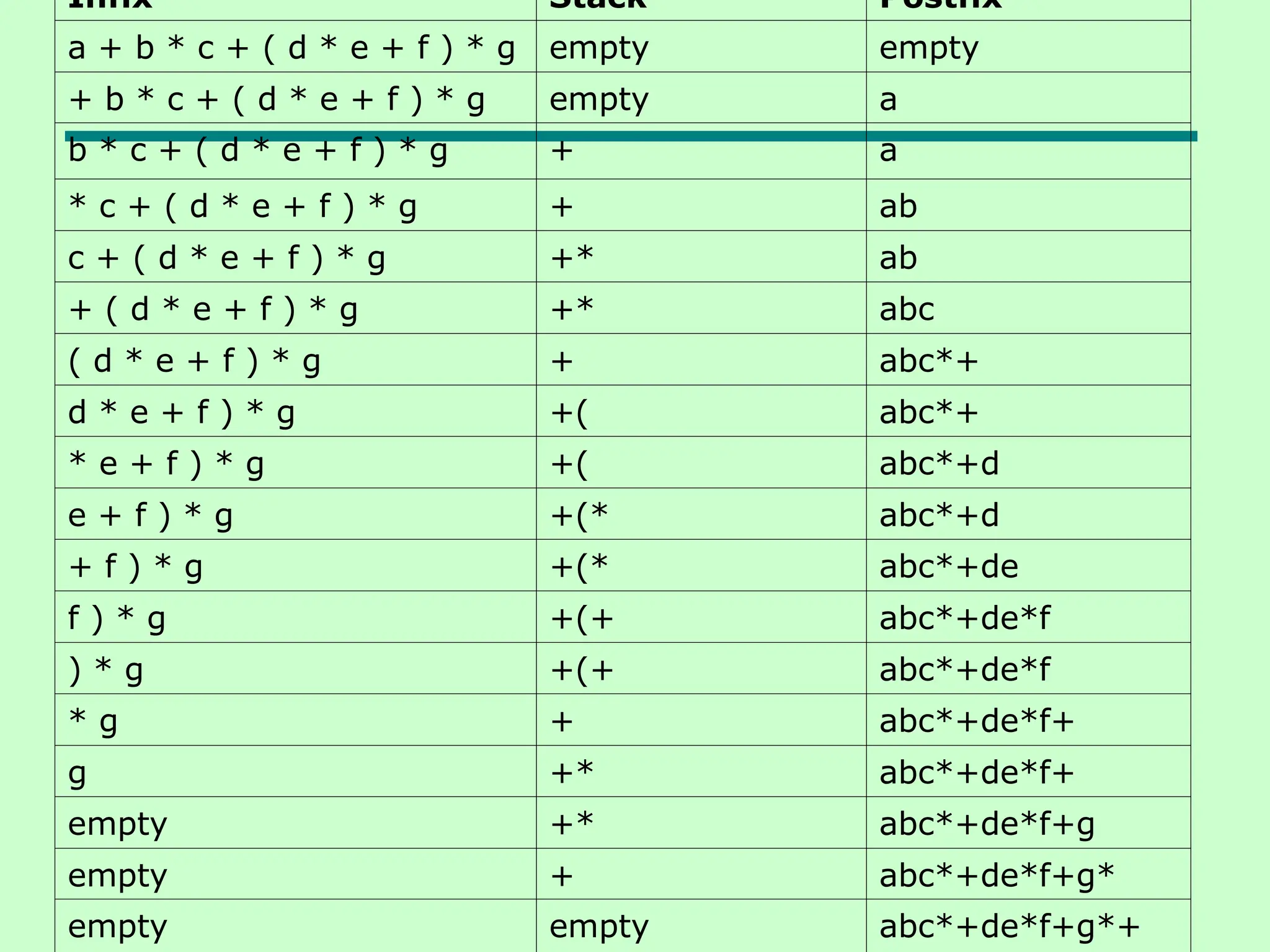
The document discusses stack and queue data structures, focusing on their definitions, operations, and implementations. It explains the stack's LIFO (last-in, first-out) policy along with its operations such as push, pop, and peek, while also covering the FIFO (first-in, first-out) policy of queues and their respective enqueue and dequeue operations. Additionally, it provides algorithms for converting infix expressions to postfix and evaluating postfix expressions.

1. week 7,8,10,11
Stack and
Stack and
Queue Data
Queue Data
Structure
Structure
12/22/24 1

2. What is Stack?
What is Stack?
• The stack is a list-like structure in which elements may be
inserted or removed from only one end.
• While this restriction makes stacks less flexible than lists, it also
makes stacks both efficient (for those operations they can do)
and easy to implement.
• Stack works on the “LIFO” policy, which stands for “Last-In, First-
Out.” Note that one implication of the LIFO policy is that stacks
remove elements in reverse order of their arrival.

3. CONT…
• A stack is generally implemented with only three principle
operations:
— push( ): Adds or inserts an item to a stack.
— pop( ): Extracts the most recently pushed item from the stack.
— Peek() - This returns the top data value of the stack
• Sometimes, the following two other methods are added.
— top( ): Returns the item at the top without removing it
— isempty( ): Determines whether the stack has anything in it
• Note that a pop( ) or top( ) operations on an empty stack is considered as an error
operation in the stack ADT.
• The result of an illegal attempt to pop or access an item from an empty stack is
called stack underflow.
• There is no upper limit on the number of items that may be kept in a stack, since
the definition does not specify how many items are allowed in the collection.
• During implementation of stack, however, running out of space could be an error
(called stack overflow).

4. Stack applications in data structure
• Stacks can be used for expression evaluation.
• Stacks can be used to check parenthesis matching in an
expression.
• Stacks can be used for Conversion from one form of
expression to another.
• Stacks can be used for Memory Management.
• Stack data structures are used in backtracking problems

5. Stack infix to postfix conversion
• Three ways of writing arithmetic expressions
• Prefix: Operands are preceded by operator. E.g.
+a b
• • Infix: Usual (natural) way of writing, operand,
then operator, and finally operand.
E.g. a + b, a+b*c
• • Postfix: Operands are followed by operator.
E.g. a b+, a b+c*, a b c*+

6. Postfix evaluation
• The time to evaluate a postfix expression is O(n)
• The following is a simple algorithm to perform postfix
evaluation:
Scans characters in given expression from left to right.
If character is an operand
Push it onto stack
If character is an operator
Pop two operands from stack.
Apply operator to these two operands.
Push the result onto stack.

7. • For instance, the postfix expression,
6 5 2 3 + 8 + 3 + is evaluated as follows:
∗ ∗
• The first four symbols are placed on the stack with
operation push ( )

8. CONT…

9. CONT…

10. Infix to Postfix Conversion
The following is a simple algorithm to convert infix expression to postfix:
Scans characters in given expression from left to right.
If character is an operand
Immediately place onto the output
If character is an operator
If top operator has lower priority or left parentheses
Push operator onto stack
Otherwise
Pop operator from the stack and place onto the output until find an entry
of lower priority or until we find left parentheses
If character is parenthesis
If it is right parentheses
Pop entries from the stack and place onto the output until find left
parentheses, pop the left parentheses too but do not place onto the output
Otherwise
Push the left parenthesis onto stack
If no character (reach end of the expression)
Pop entries from the stack and place onto the output until the stack is empty

11. CONT…
• To see how this algorithm performs, we will
convert infix expression to postfix
a + b * c + ( d * e + f ) * g

12. Infix Stack Postfix
a + b * c + ( d * e + f ) * g empty empty
+ b * c + ( d * e + f ) * g empty a
b * c + ( d * e + f ) * g + a
* c + ( d * e + f ) * g + ab
c + ( d * e + f ) * g +* ab
+ ( d * e + f ) * g +* abc
( d * e + f ) * g + abc*+
d * e + f ) * g +( abc*+
* e + f ) * g +( abc*+d
e + f ) * g +(* abc*+d
+ f ) * g +(* abc*+de
f ) * g +(+ abc*+de*f
) * g +(+ abc*+de*f
* g + abc*+de*f+
g +* abc*+de*f+
empty +* abc*+de*f+g
empty + abc*+de*f+g*
empty empty abc*+de*f+g*+

13. Implementation of a Stack
• As with lists, there are many variations on stack implementation.
The two approaches presented here are:
—array-based and
—linked stacks
 Array-Based Implementation of Stack
• Array implementation of stack is relatively straightforward
• The only limitation with this implementation is that the number of
elements in an array is fixed and is assigned by the declaration for
the array.
• A program that implements a stack using array is given as follows.
— Input: Push elements 11, 22, 33, 44, 55, 66
— Output: Pop elements 66, 55, 44, 33, 22, 11

14. CONT…
 Stack size and initial value of top should be
defined globally
—int stack[100], n=100, top=-1;
• the push() function takes argument val i.e. value
to be pushed into the stack.
• If a top is greater than or equal to n, there is no
space in a stack and overflow is printed.
Otherwise, val is pushed into the stack.

15. CONT…
• The pop() function pops the topmost
value of the stack, if there is any value.
• If the stack is empty then underflow is
printed.

16. CONT…
• The display() function displays all the
elements in the stack.
• If there are no elements in the stack, then
Stack is empty is printed.

17. Linked list Implementation of Stack
• second implementation of a stack uses a
singly linked list
• push (insert) and pop (delete) element
perform at the front of the list.

18. Implementing Operations on Linked List
Implementation of Stack
• the structure Node is used to create the
linked list that is implemented as a stack
struct Node {
int data;
Node *next; };
Node* top = NULL;
PUSH Operation: push function inserts
an element (or new node) at the front of
the list.
• There is no need to test whether or not
stack is full (dynamic allocation of space)
because there is no upper limit.

19. void push(int val)
{
Node *temp =new node
temp->data= val;
Temp->next=top;
top = new node;
}

20. POP Operation: POP operation performs
the following function.
• If stack is empty, it prints a warning message
and halts program execution.
• Removes the element at the front of the list.
void pop()
{
if(top==NULL)
cout<<"Stack Underflow"<<endl;
else
{
cout<<"The popped element is "<< top->data
<<endl;
top = top->next; } }

21. Queue ADT
• Like the stack, the queue is a list-like
structure that provides restricted access
to its elements.
• Queue elements may only be inserted at
the back (called an enqueue operation)
and removed from the front (called a
dequeue operation).
• Queue works on the “FIFO” policy, which
stands for “First-In, First-Out.”

22. • Queue Operations:
• enqueue( ): Adds or append item onto queue
at the back or rare.
• dequeue( ): Extracts or deletes item from
queue at the front.
Eg. Enqueue(c)
• Enqueue (B) C | B| A
• Enqueue(A)
• Dequeue() ... .... B| A
• Enqueue(D) . ........ B| A |D
• Dequeue().......... A|D

23. Implementations of Queues
• Array
• Circular Array
• Linked List

24. • Array-Based Implementation of
Queue
• InitializeQueue:
int queue[100];
int n = 100;
int front = - 1;
int rear = - 1;

25. • EnQueue(item):
void enqueue() {
int val;
if (rear == n - 1)
cout<<"Queue Overflow"<<endl;
else {
if (front == - 1)
front = 0;
cout<<"Insert the element in queue : "<<endl;
cin>>val;
rear++;
queue[rear] = val; }}

26. • DeQueue(item):
void dequeue() {
if (front == - 1 || front > rear) {
cout<<"Queue Underflow ";
}
else {
cout<<"Element deleted from queue is : "<<
queue[front] <<endl;
front++;;
} }

27. Reading Assignment
• Implementations of Queues
Circular Array
Linked List

28. Quiz
1. Evaluate the given post fix arithmetic
expressions. 6 5 2 3 + 8 + 3 +
∗ ∗
2. Compare and contrast array and linked
list. Support your answers with example.