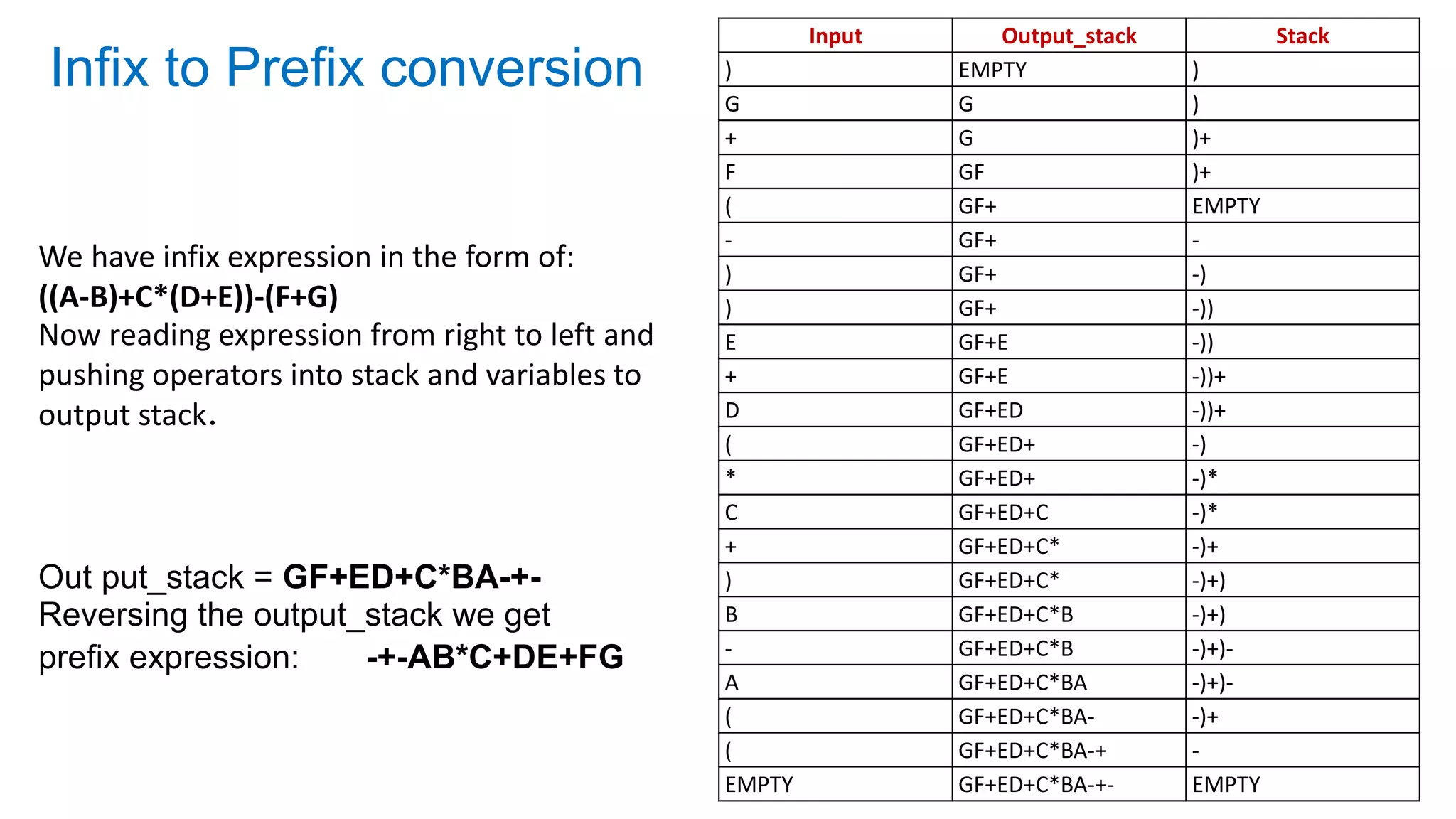
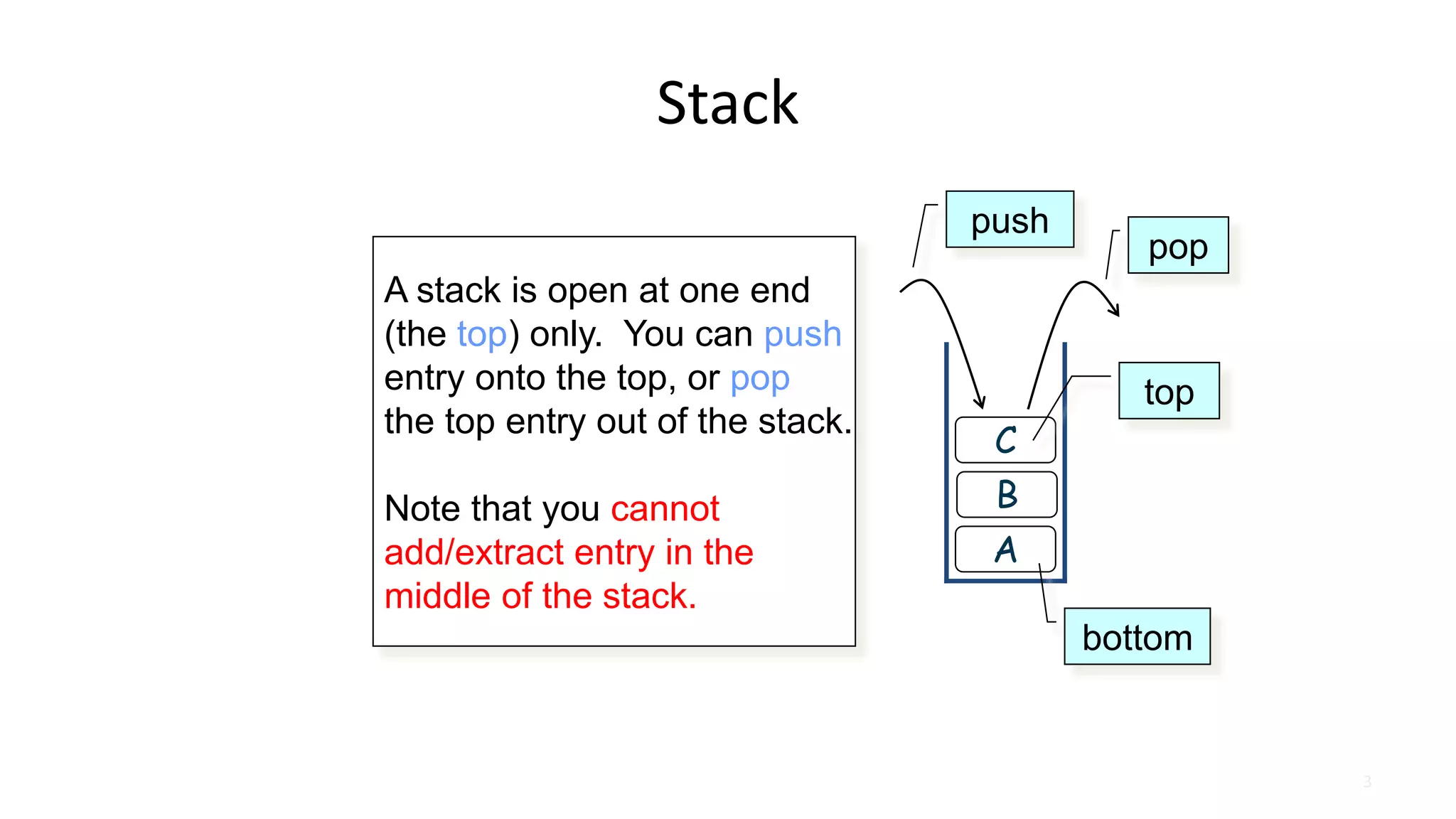
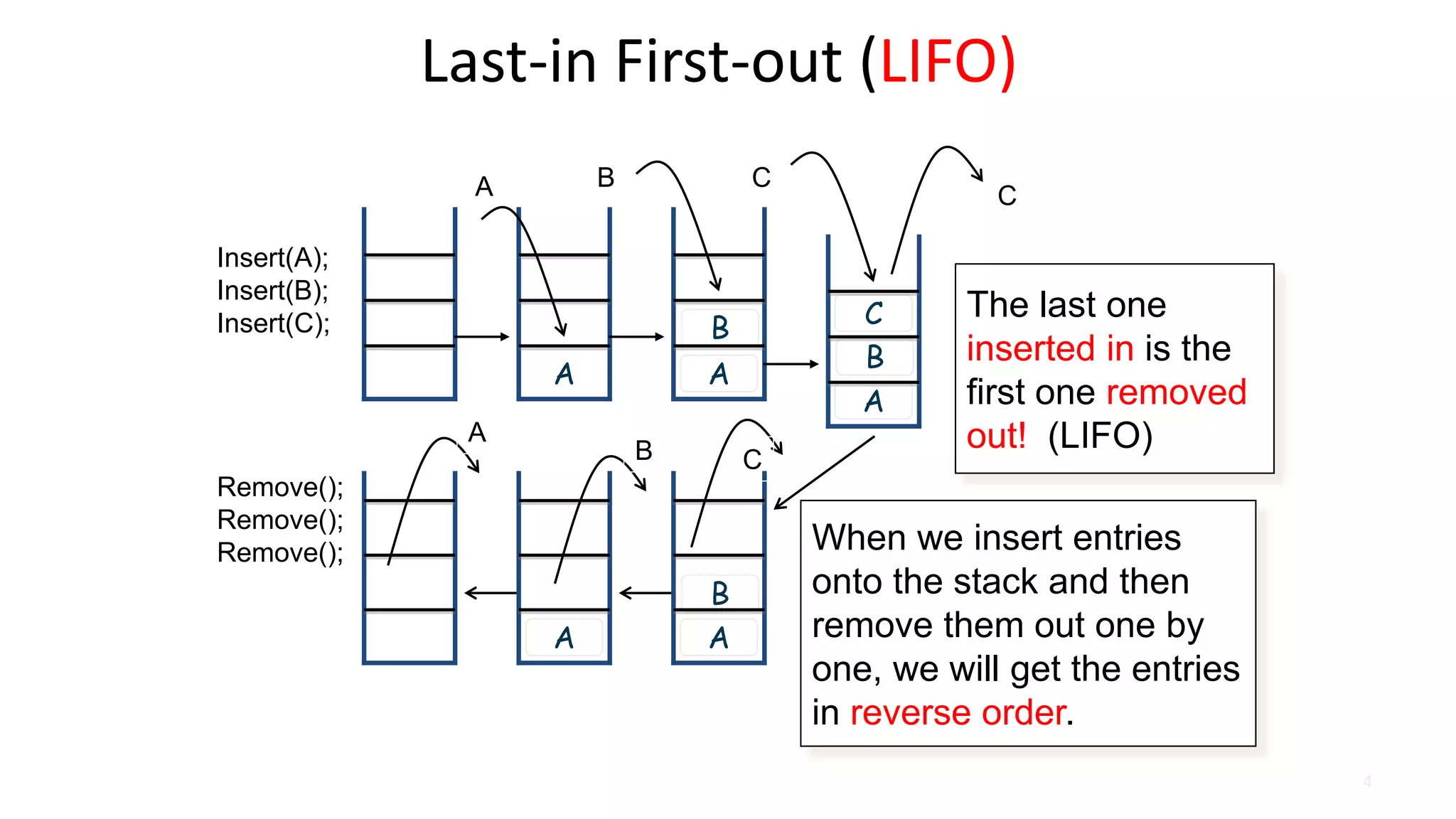
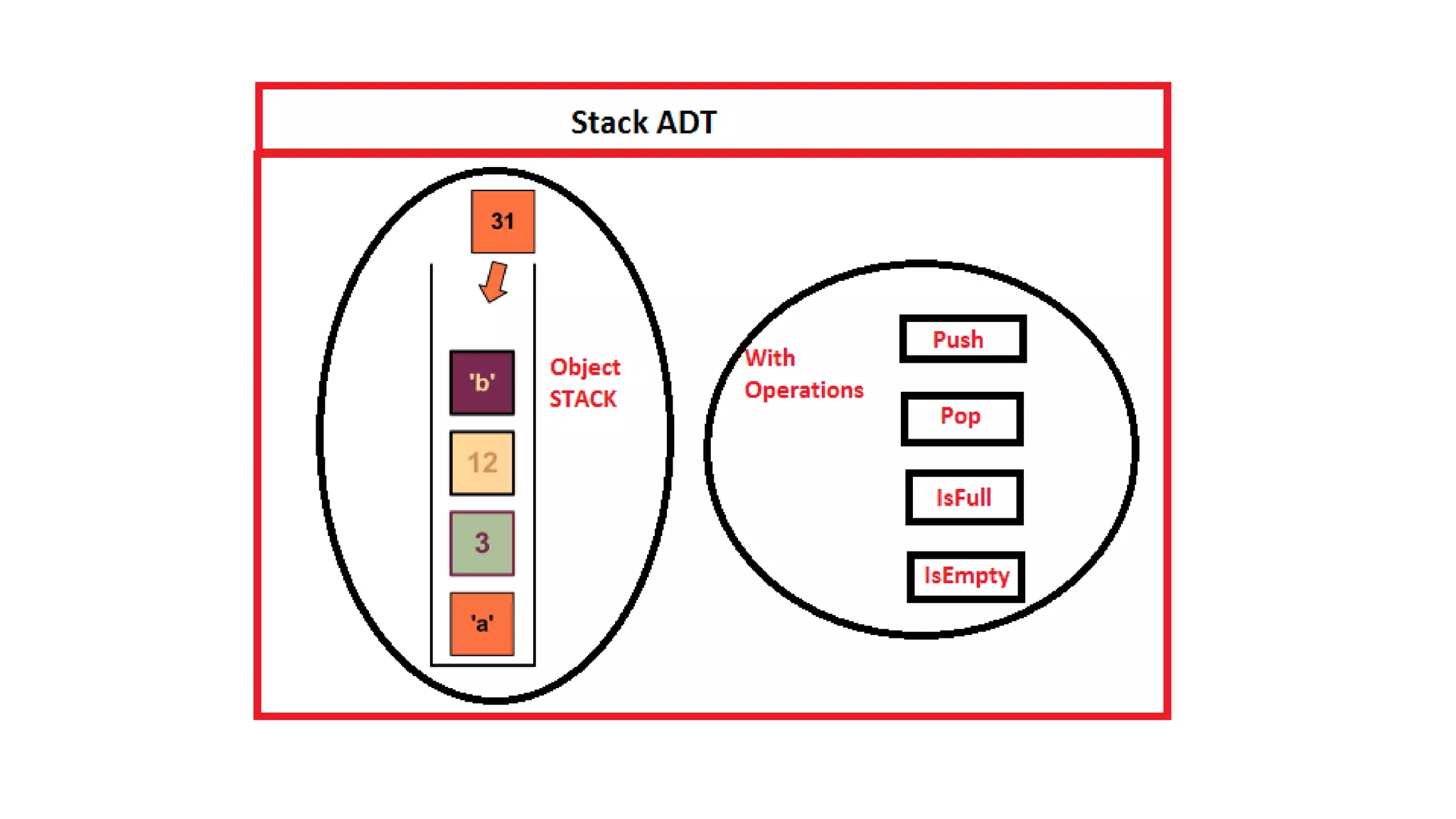
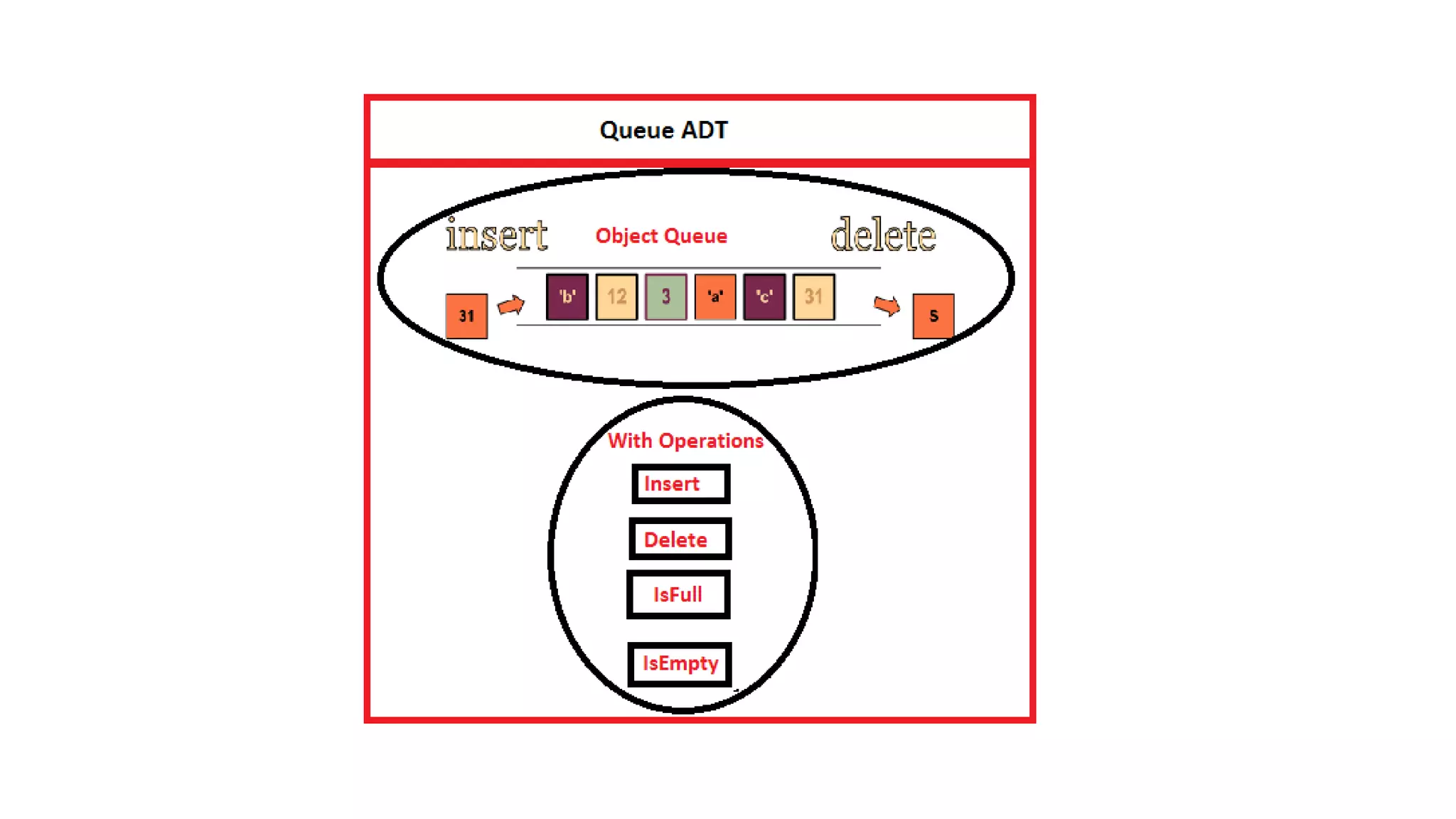
Stack is an abstract data type that serves as a linear collection of elements. It has two main operations: push, which adds an element to the top of the stack, and pop, which removes the top element. A stack follows last-in, first-out (LIFO) order, meaning the last element added is the first removed. Common real-world examples of stacks include piles of plates and books.










![#define stack_size 6;
int top;
char stack[stack_size];
stack implementation by an array
top = 2
stack
stack
?
?
?
?
?
?
0
1
2
3
4
5 (stacksize-1)](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-17-2048.jpg)

![19
Push(X)
void push(char X)
{
if(top >= stack_size-1)
cout<<“Overflow: stack is full”;
else
{
top++; /increase top by 1
stack[top] = X; /insert the item on top
}
}
X
?
?
?
?
?
top= 0 1
entry
top
top++;
stack[top] = X;
Stack[++top] = X;
0
1
2
3
4
5 (stacksize-1)
Before insertion it needs
first to check the
overflow situation i.e.
stack is full or not full](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-19-2048.jpg)
![Pop()
void pop() //pop function is not returning
{
if(top<0)
cout<<"underflow: stack is empty”;
else
{
char X = stack[top];
top--;
}
}
top= 10
entry
top
?
?
?
?
?
?
0
1
2
3
4
5
E--1ntry
Before deletion it needs
first to check the
underflow situation i.e.
stack is empty or not
empty
char X = stack[top];
top--;
char X = stack[top--];](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-20-2048.jpg)
![Pop() //pop function is returning the top element
char pop()
{
if(top<0)
cout<<"underflow: stack is empty”;
else
{
char X = stack[top];
top--;
return X;
}
} top= 10
entry
top
?
?
?
?
?
?
0
1
2
3
4
5
E--1ntry](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-21-2048.jpg)
![Top()
char Top() //top function is returning top value
{
return stack[top]; //but not reduce top index
} top= 10
entry
top
K
R
?
?
?
?
0
1
2
3
4
5](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-22-2048.jpg)


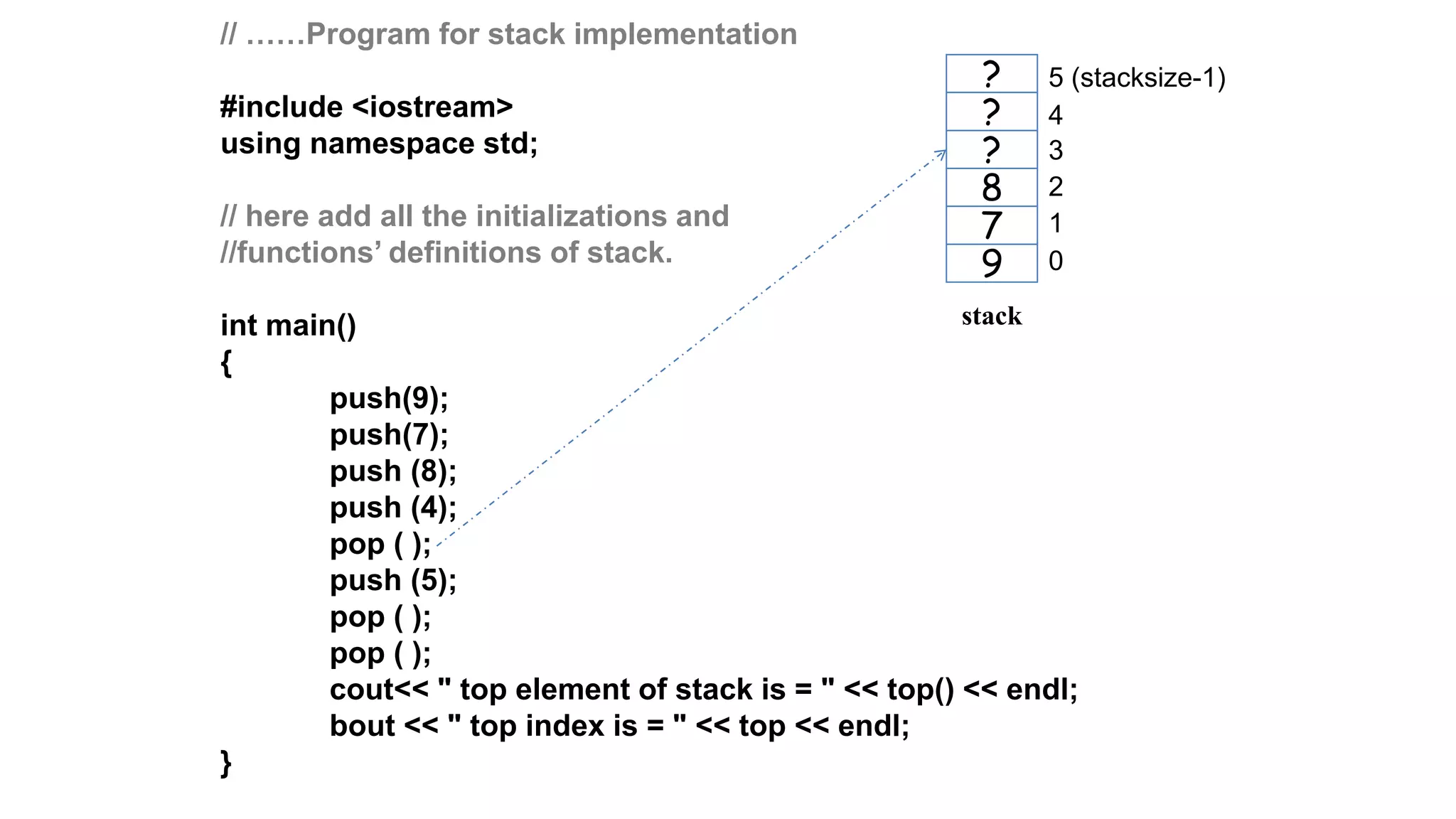
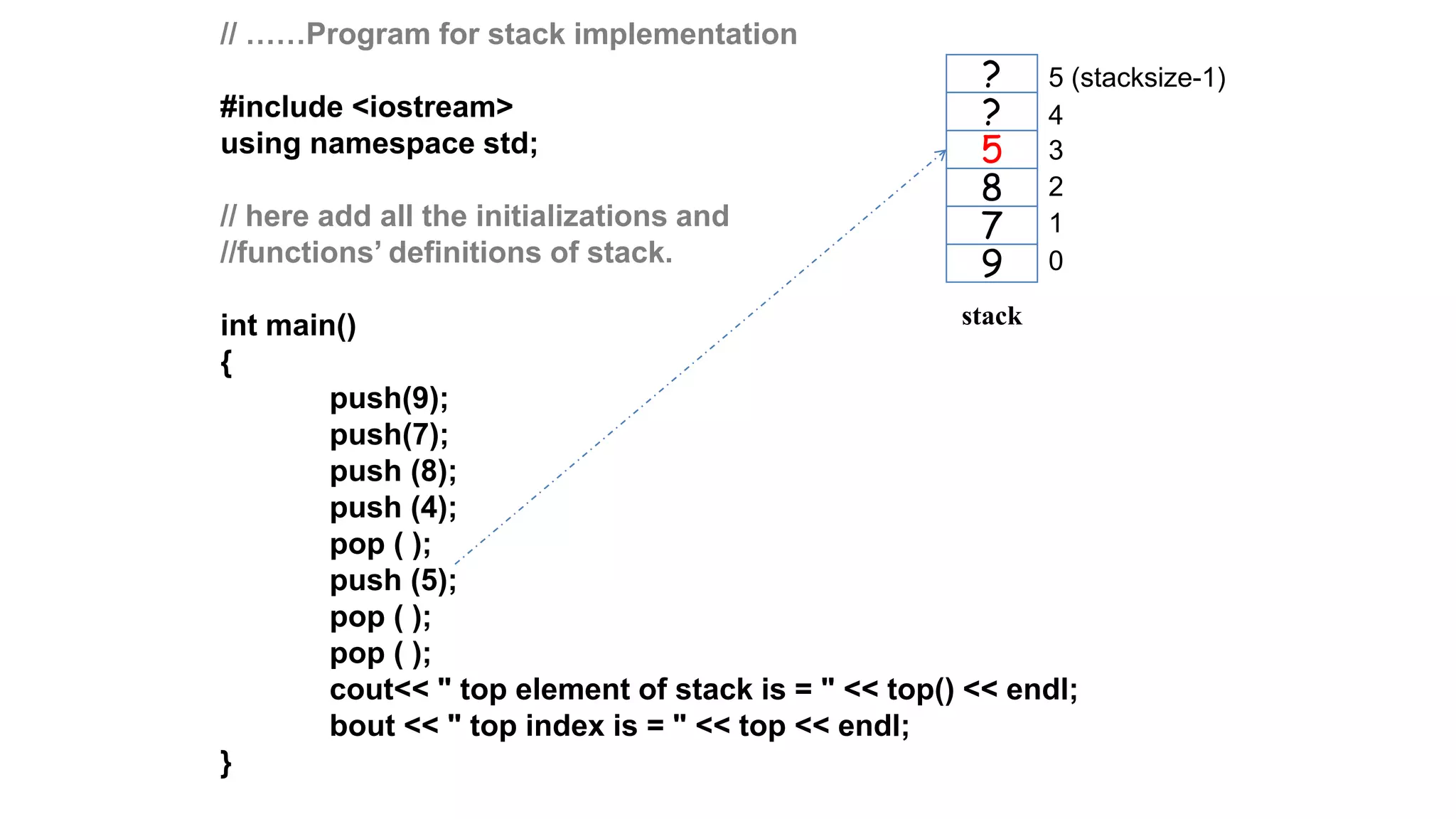

![28
Traversing a stack
void show()
{
int i;
for(i=top; i>=0; i--)
cout<< “ “<<stack[i];
}
OUTPUT:
D C B A
A
B
C
D
?
?
top
0
1
2
3
Stack[ ]](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-28-2048.jpg)
![Stack
int Stack[100], Top=-1; // Stack holds the elements;
// Top is the index of Stack always pointing to the
first/top element of the stack.
bool IsEmpty( void ); // returns True if stack has no
element
bool IsFull( void ); // returns True if stack full
bool Push( int Element ); // inserts Element at the top of
the stack
bool Pop( int *Element ); // deletes top element from stack
into Element
bool TopElement( int *Element ); // gives the top element
in Element
void Show( void ); // prints the whole stack](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-29-2048.jpg)


![bool Push( int Element ){
// inserts Element at the top of the stack
if( IsFull( ) )
{ cout << "Stack is Fulln"; return false; }
// push element if there is space
Stack[ ++Top ] = Element;
return true;
}
6
5
4
3
2 C
1 B
0 A
Top
Considering Size = 7
There are 3 elements inside Stack
So next element will be pushed at index 3](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-32-2048.jpg)
![bool Pop( int *Element ){
// deletes top element from stack and puts it in
Element
if( IsEmpty() )
{ cout << "Stack emptyn"; return false; }
*Element = Stack[ Top-- ];
return true;
}
6
5
4
3 D
2 C
1 B
0 A
Top
Considering Size = 7
There are 4 elements inside Stack
So element will be popped from index 3](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-33-2048.jpg)
![bool TopElement( int *Element ){
// gives the top element in Element
if( IsEmpty() )
{ cout << "Stack emptyn"; return false; }
*Element = Stack[ Top ];
return true;
}
Considering Size = 7
There are 4 elements inside Stack
So top element will be at index 3
6
5
4
3 D
2 C
1 B
0 A
Top](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-34-2048.jpg)
![void Show( void ){
// prints the whole stack
if( IsEmpty() )
{ cout << "Stack emptyn"; return; }
for( int i=Top; i>=0; i-- ) cout << Stack[i] <<endl;
}
6
5
4
3 D
2 C
1 B
0 A
Considering Size = 7
There are 4 elements inside Stack
So element will be shown from index
3 down to index 0.
Top](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-35-2048.jpg)
![Creating a class for Stack
class MyStack{
int Stack[MaxSize], Top, MaxSize=100;
public:
//Initializing stack
MyStack( int Size = 100 ){ MaxSize = Size; Top = -1;}
bool IsEmpty( void );
bool IsFull( void );
bool Push( int Element );
bool Pop( int &Element );
bool TopElement( int &Element );
void Show( void );
void Reset( void ){ Top = -1; } //Re-start the stack
};](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-36-2048.jpg)


![The Constructor will create the array dynamically, Destructor will
release it.
MyStack::MyStack( int Size ){
MaxSize = Size; // get Size
Stack = new int[ MaxSize ]; // create array
acordingly
Top = 0; // start the stack
}
MyStack::~MyStack( void ){
delete [] Stack; // release the memory for
stack
}](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-39-2048.jpg)
![Resize creates a new array dynamically, copies all the element from the
previous stack, releases the old array, and makes the pointer Stack point to
the new array.
User can define the additional size. Use negative size to decrease the array.
void Resize( int Size ){
// creates a new stack with MaxSize + Size
int *S = new int[ MaxSize + Size ];
// copy the elements from old to new stack
for( int i=0; i<MaxSize; i++ ) S[i] = Stack[i];
MaxSize += Size; // MaxSize increases by Size
delete [] Stack; // release the old stack
this.Stack = S; // assign Stack with new stack.
}](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-40-2048.jpg)
![void Push( int Element ){
// inserts Element at the top of the stack
if( StackFull( ) ) Resize( 5 ); // increase
size if full
Stack[ ++Top ] = Element;
}](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-41-2048.jpg)







![Example:
[(A+B)-{(C+D)-E}]
Symbol Stack
[ [
( [(
A [(
+ [(
B [(
) [
- [
{ [{
( [{(
C [{(
+ [{(
D [{(
) [{
- [{
E [{
} [
]](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-50-2048.jpg)






![Operator Precedence and Associativity
Precedence Operator Associativity
1 :: Left-to-right
2 () [] . -> ++ -- Left-to-right
3
++ -- ~ ! sizeof new
delete
Right-to-left
* &
+ -
4 (type) Right-to-left
5 .* ->* Left-to-right
6 * / % Left-to-right
7 + - Left-to-right
8 << >> Left-to-right
Precedence Operator Associativity
9 < > <= >= Left-to-right
10 == != Left-to-right
11 & Left-to-right
12 ^ Left-to-right
13 | Left-to-right
14 && Left-to-right
15 || Left-to-right
16 ?: Right-to-left
17
= *= /= %= += -=
>>= <<= &= ^= |=
Right-to-left
18 , Left-to-right](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-57-2048.jpg)







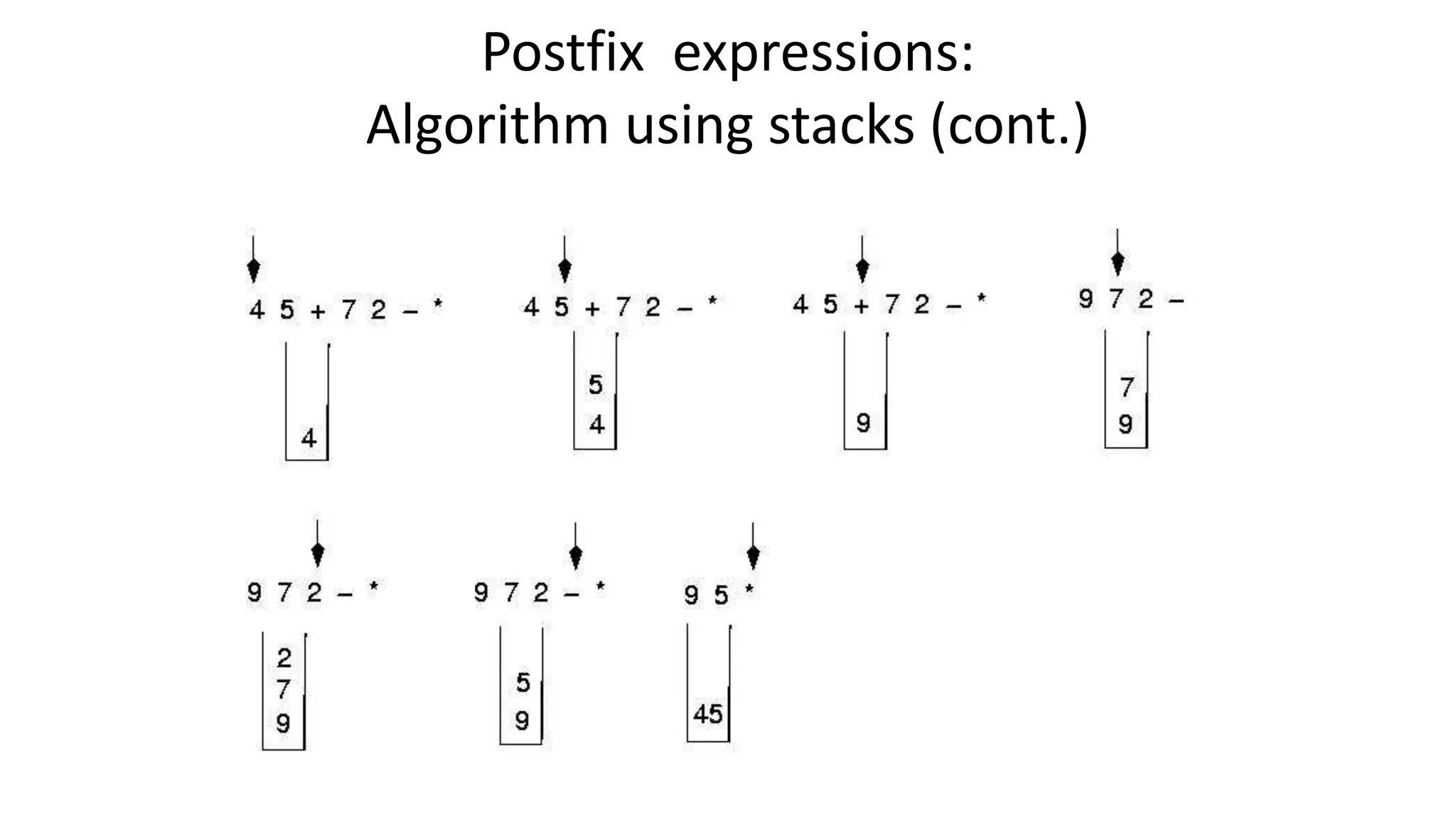
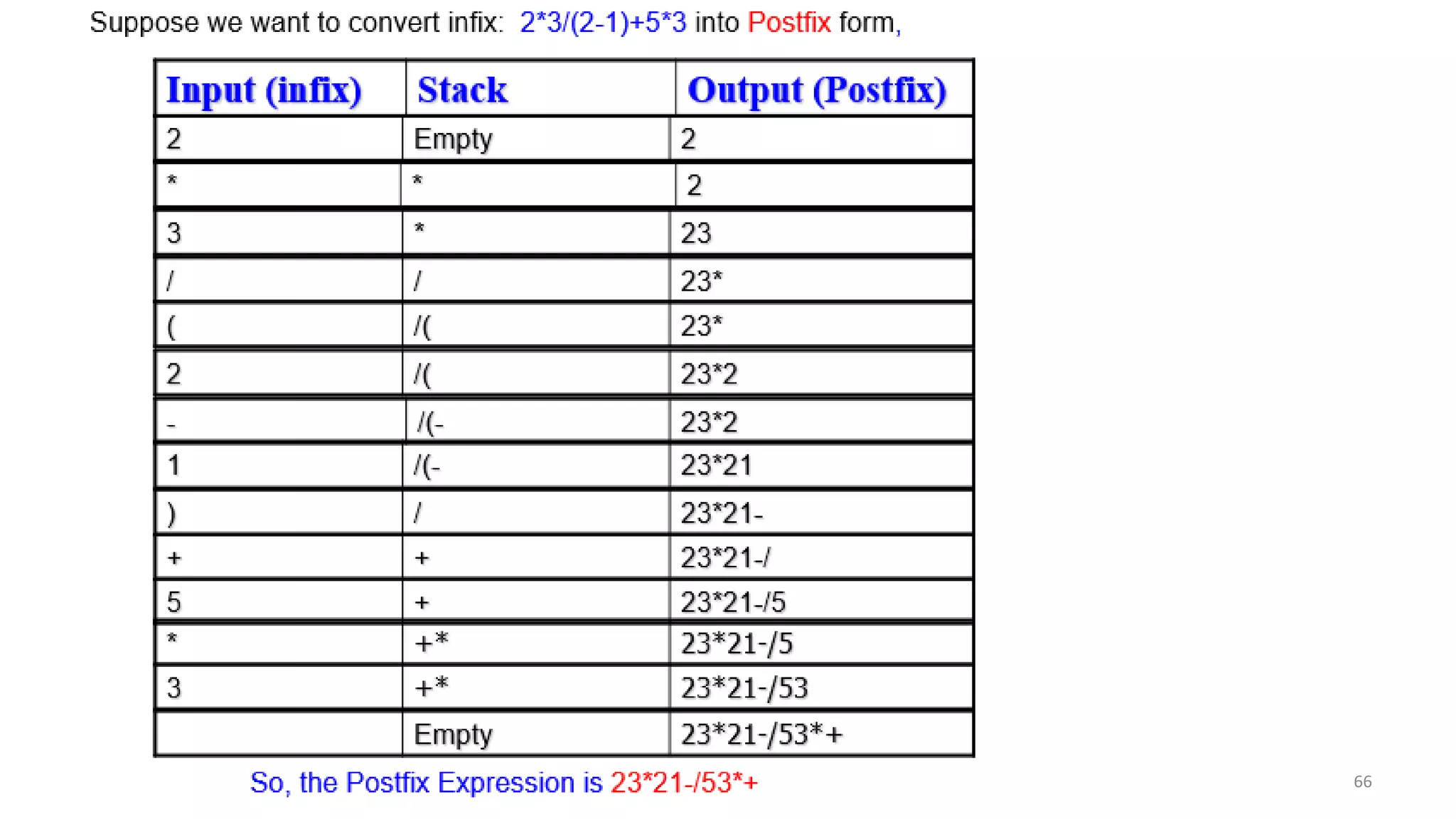
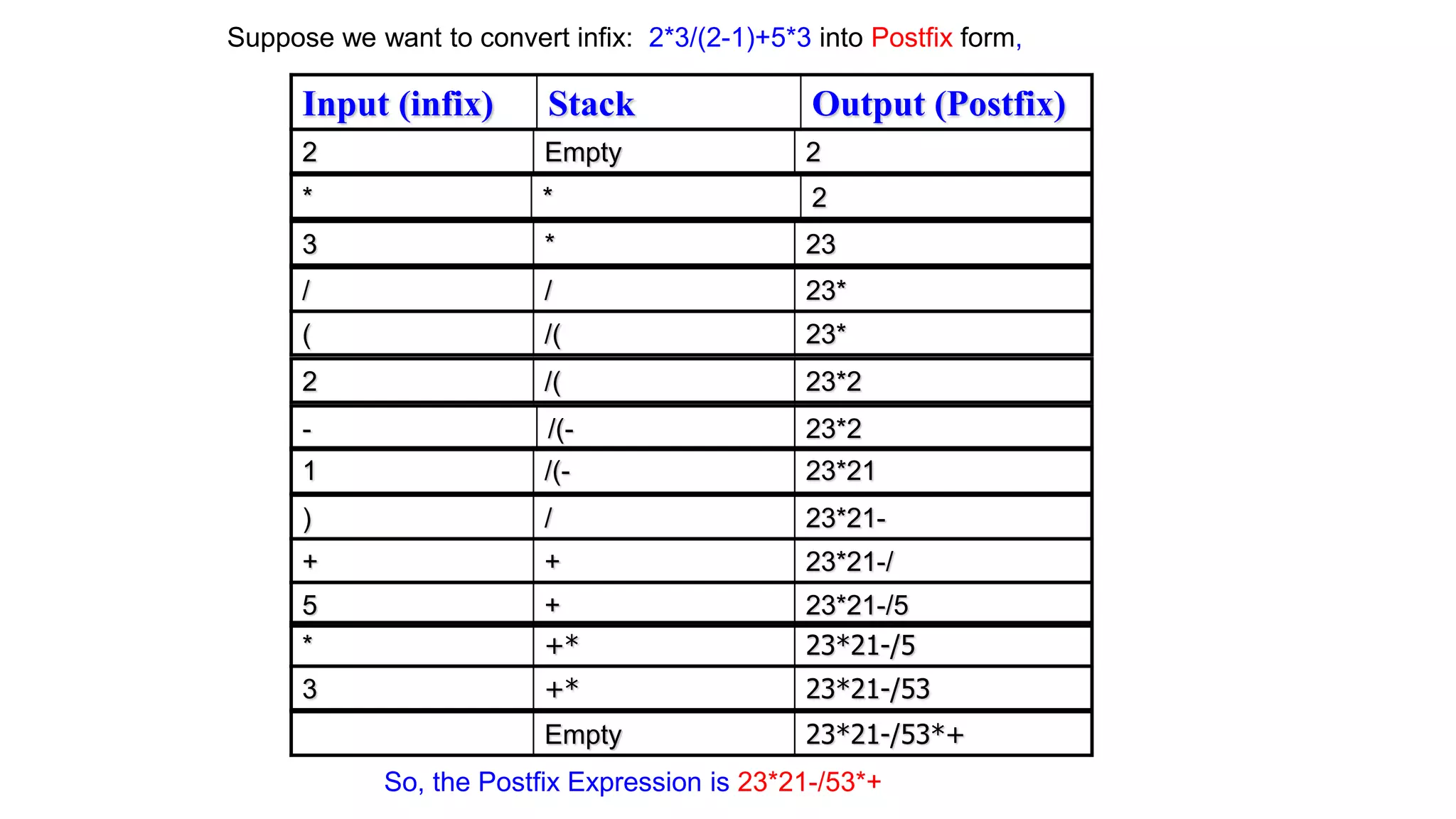
![Algorithm for Infix to Postfix conversion
1) Examine the ith element in the input, infix[i].
2) If it is operand, output it at kth location (push to postfix[k]).
3) else If it is opening parenthesis ‘(’, push it on stack.
4) else If it is a closing parenthesis ‘)’,
pop (operators) from stack and output to postfix[k] them until an opening
parenthesis ‘(’ is encountered in the top of stack.
pop and discard the opening parenthesis ‘(’ from stack.
5) else If it is an operator ‘+’, ‘-’, ‘*’, ‘/’, ‘%’ then
i) If stack is empty, push operator on stack.
ii) else If the top of stack is opening parenthesis ‘(’, push on stack
iii) else If it has higher priority than the top of stack, push on stack.
iv) else pop the operator from the stack and output it, repeat step 5
6) If there is more input in infix[], go to step 1
7) If there is no more input, pop the remaining operators to output.](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-65-2048.jpg)


![Algorithm for Infix to Postfix conversion
1) Examine the ith element in the input, infix[i].
2) If it is operand, output it at kth location (push to postfix[k]).
3) else If it is opening parenthesis ‘(’, push it on stack.
4) else If it is a closing parenthesis ‘)’,
pop (operators) from stack and output to postfix[k] them until an opening
parenthesis ‘(’ is encountered in the top of stack.
pop and discard the opening parenthesis ‘(’ from stack.
5) else If it is an operator ‘+’, ‘-’, ‘*’, ‘/’, ‘%’ then
i) If stack is empty, push operator on stack.
ii) else If the top of stack is opening parenthesis ‘(’, push on stack
iii) else If it has higher priority than the top of stack, push on stack.
iv) else pop the operator from the stack and output it, repeat step 5
6) If there is more input in infix[], go to step 1
7) If there is no more input, pop the remaining operators to output.](https://image.slidesharecdn.com/stackanditsapplications-210307130758/75/Stack-and-its-applications-70-2048.jpg)