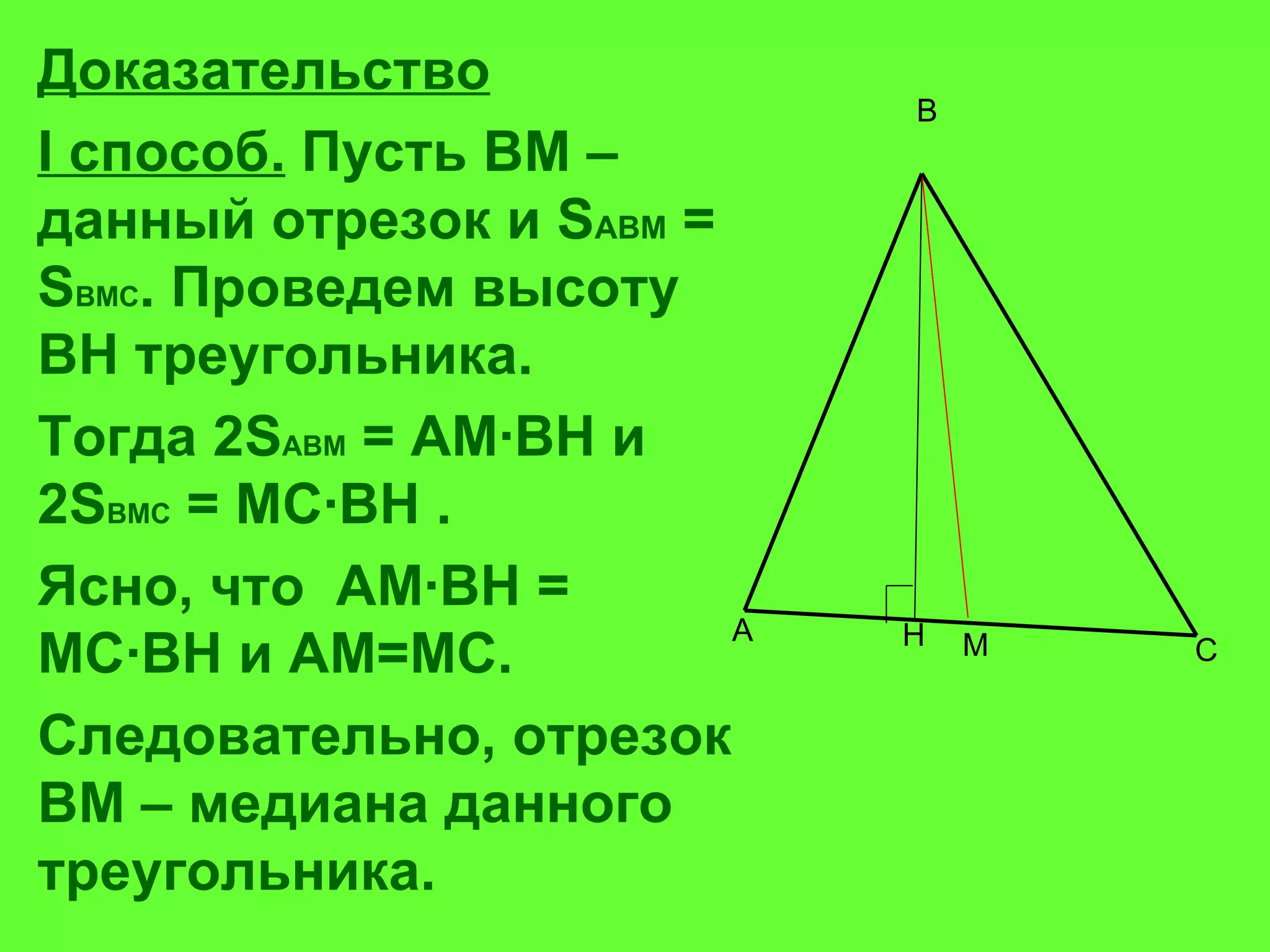
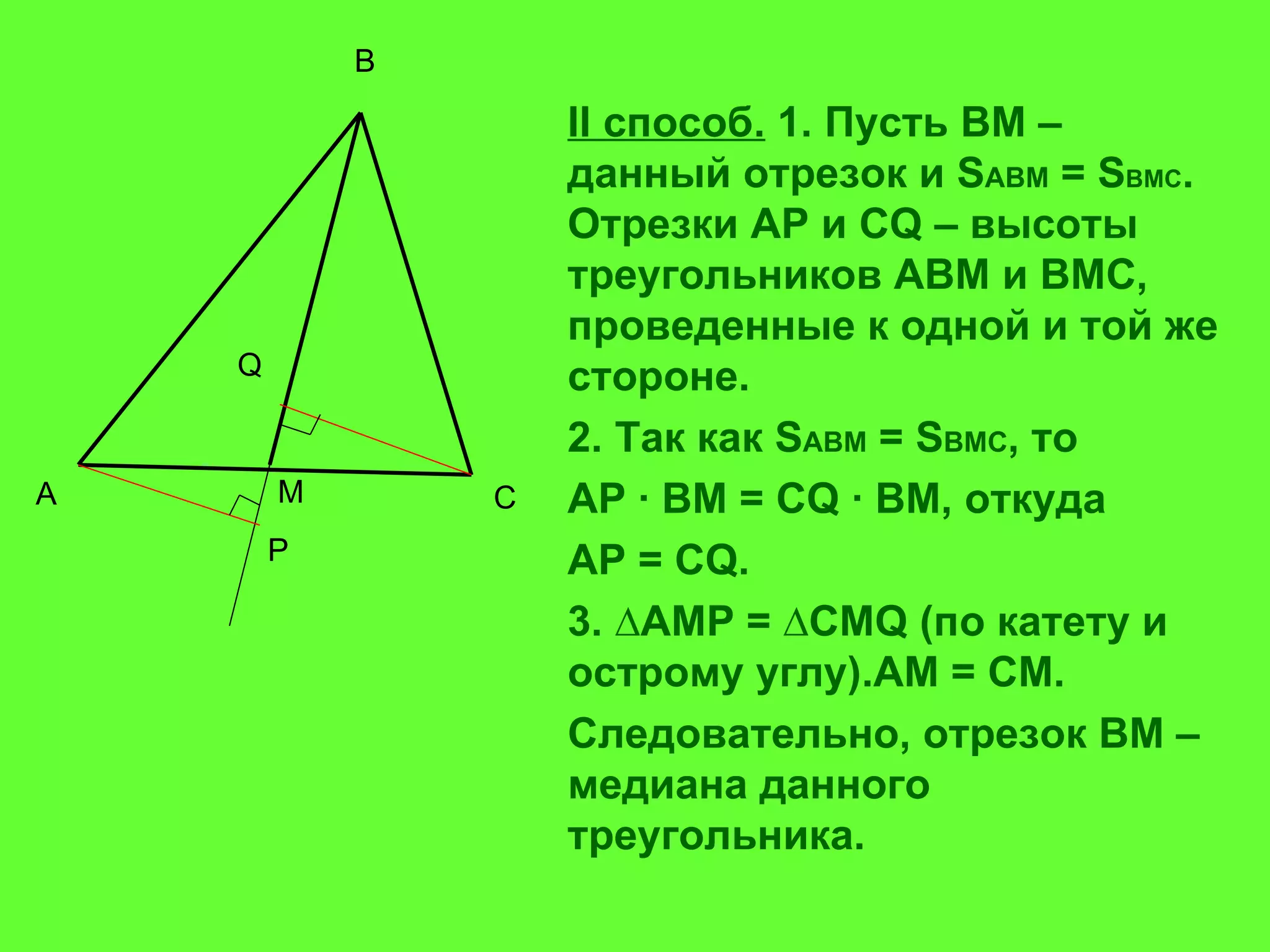
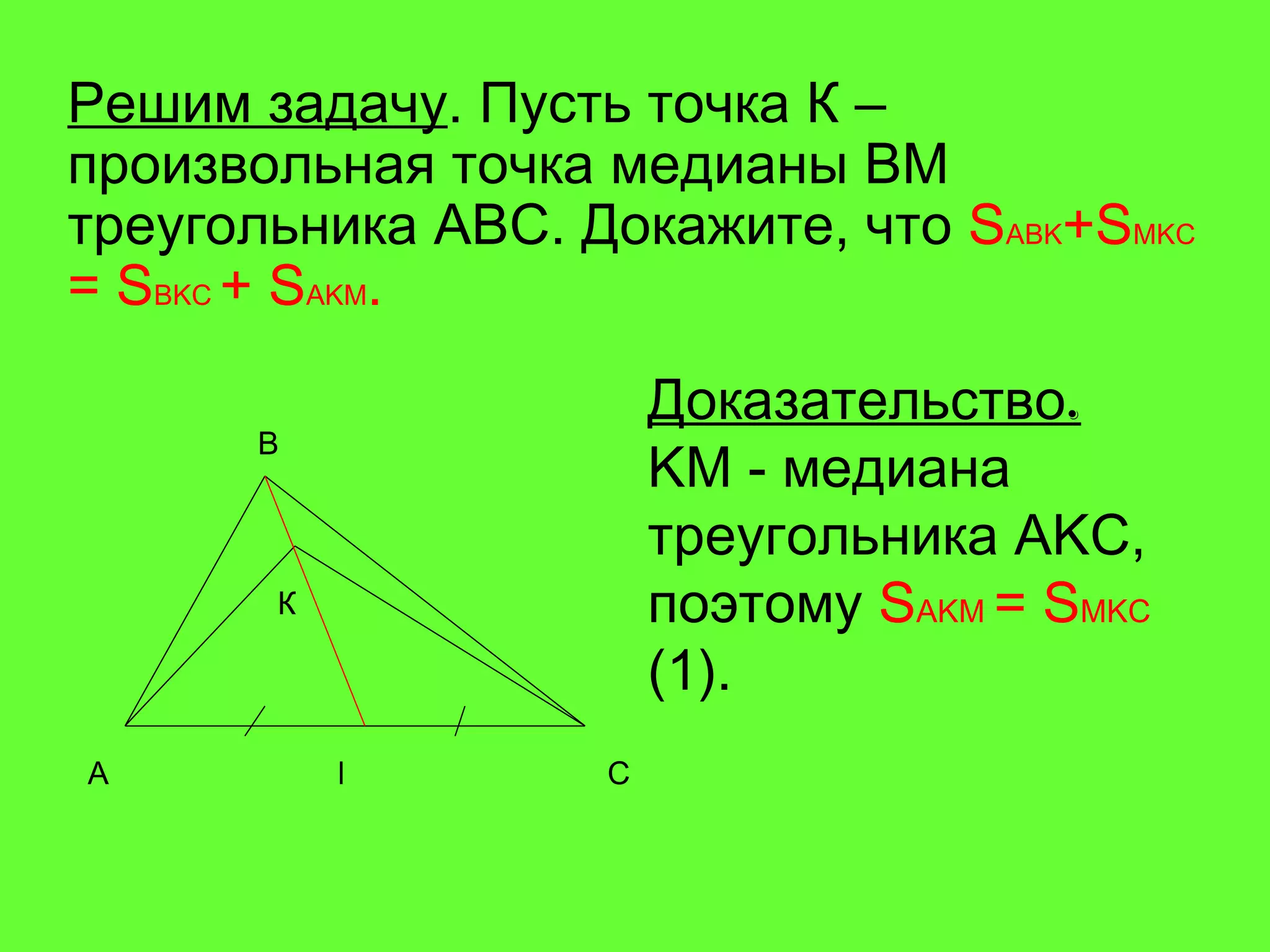
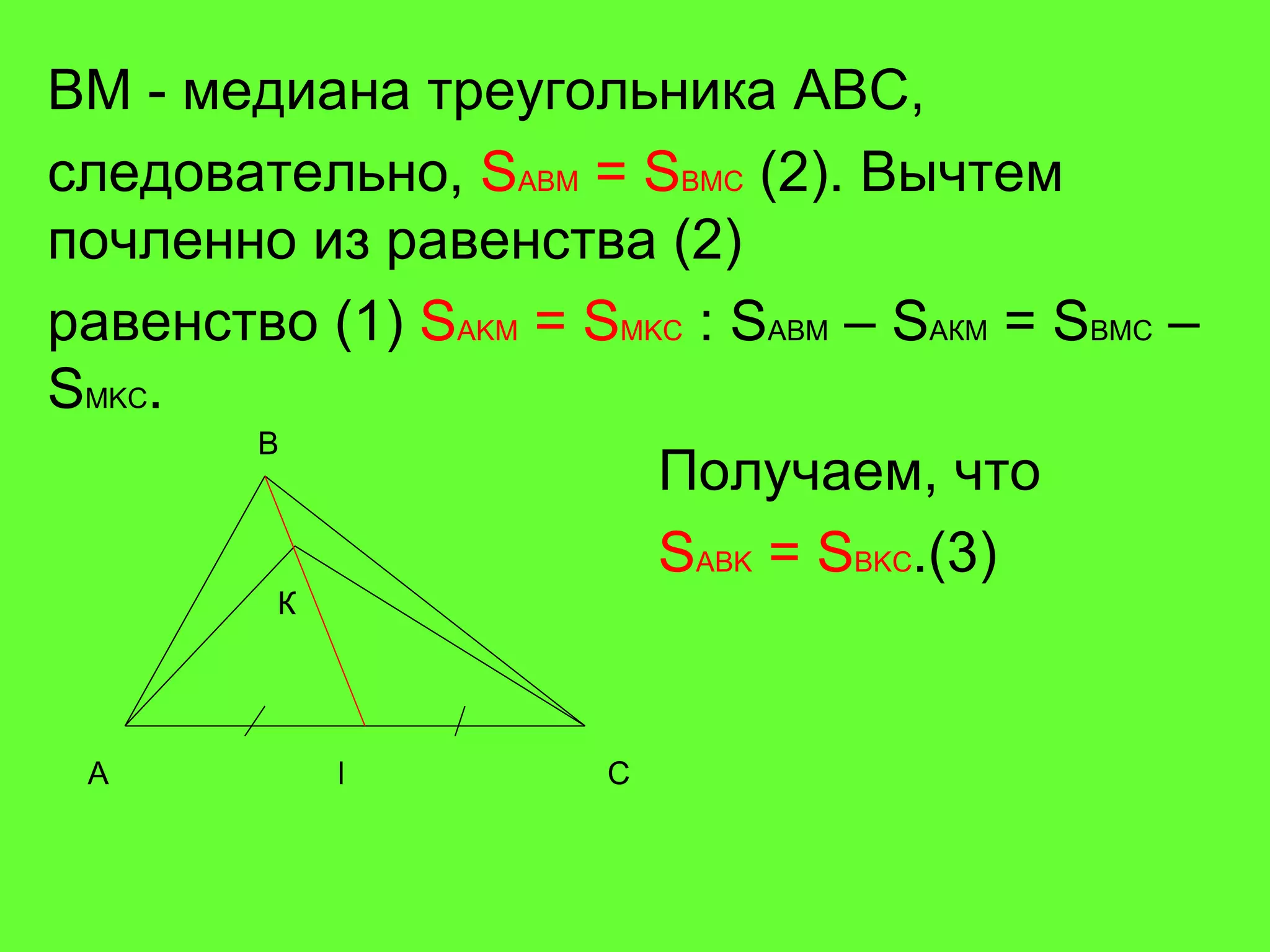
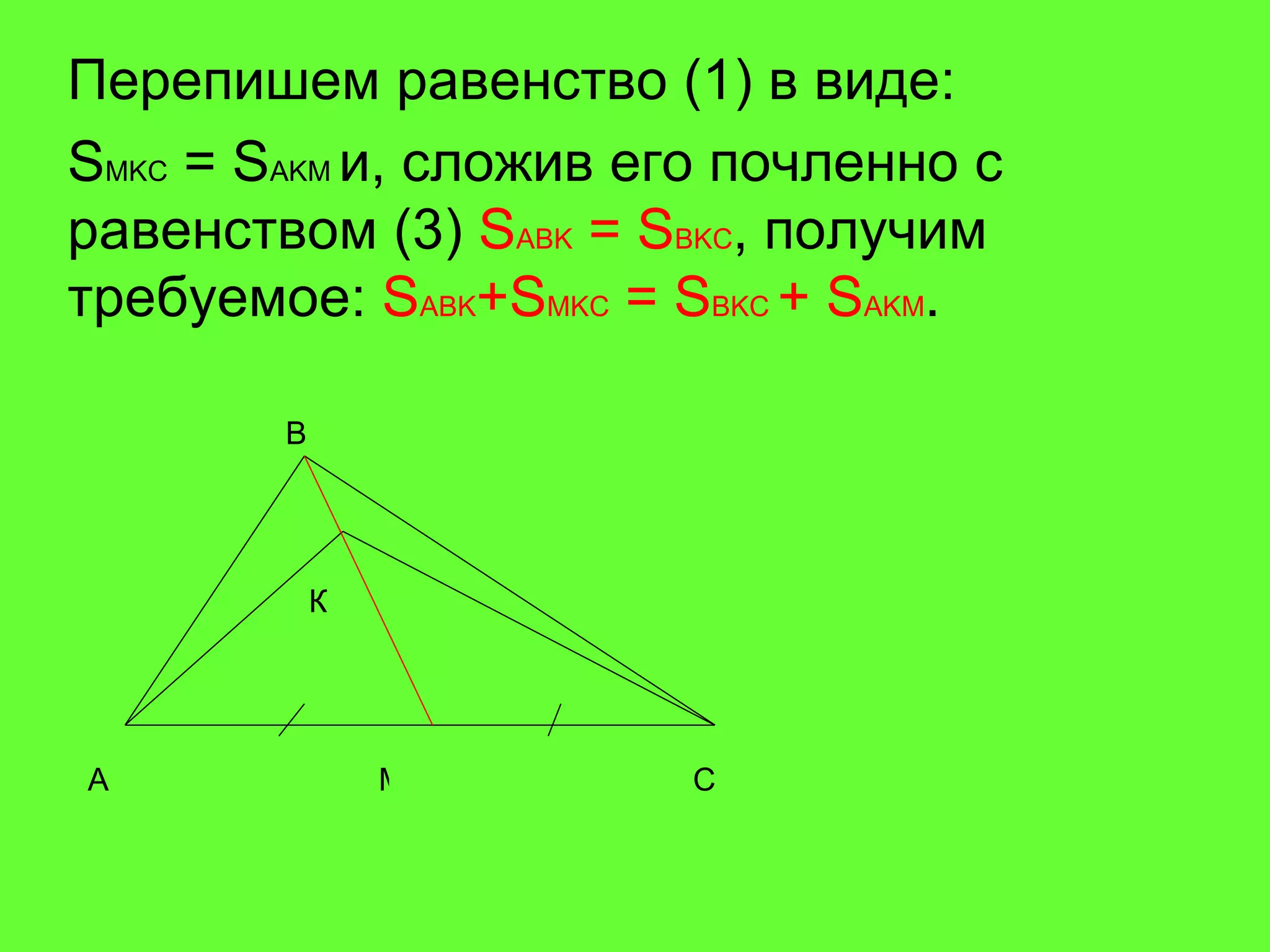
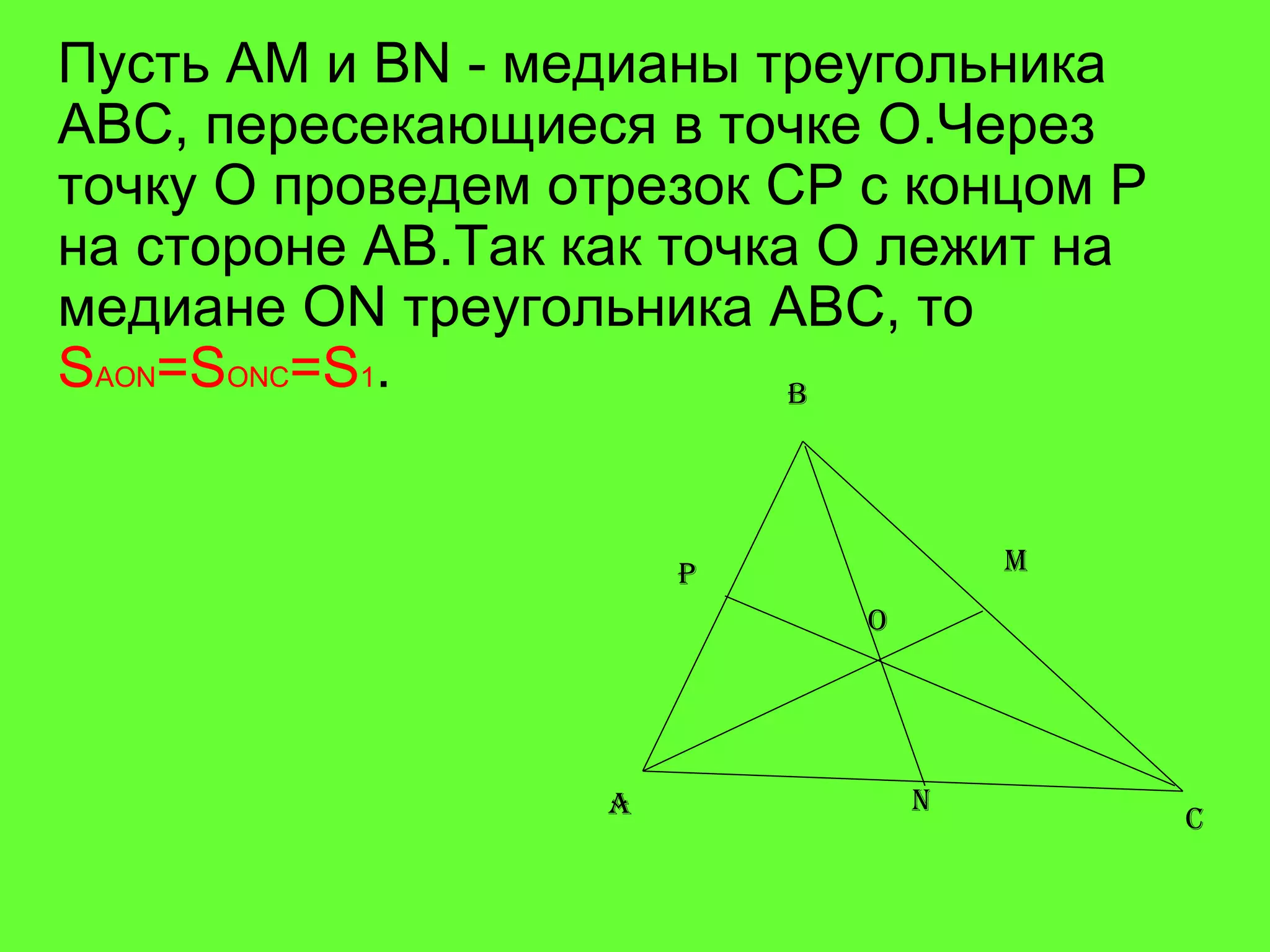
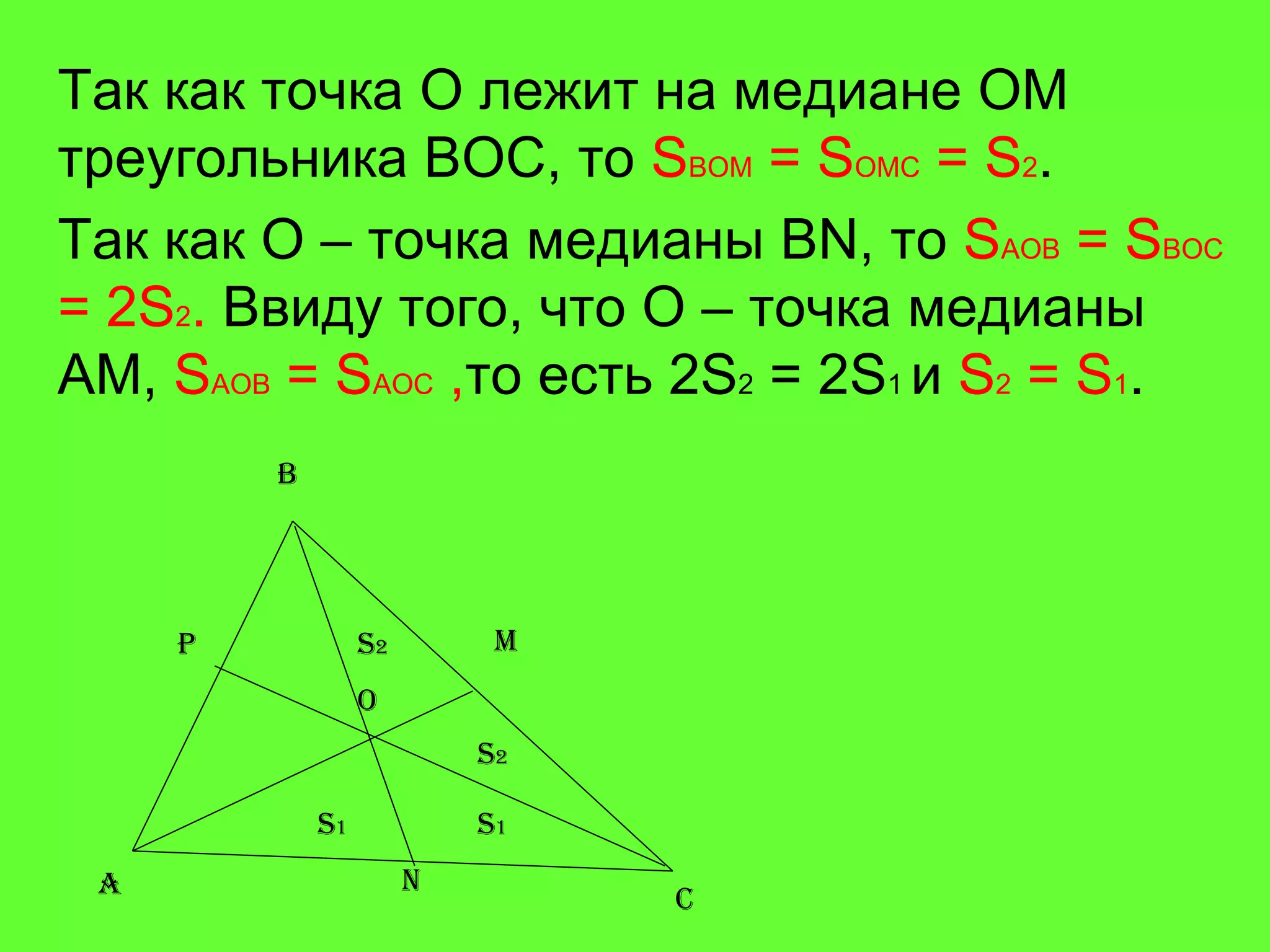
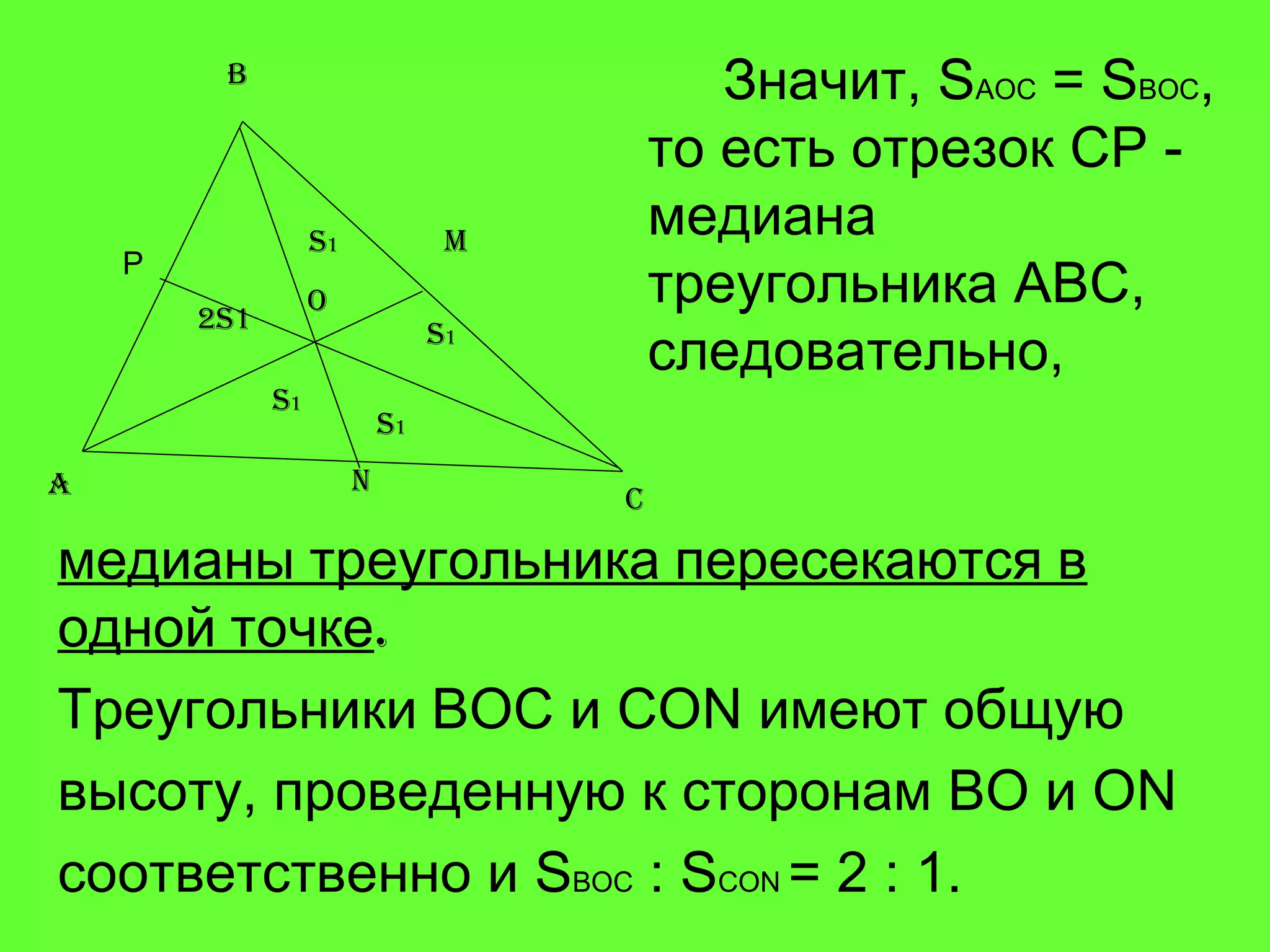
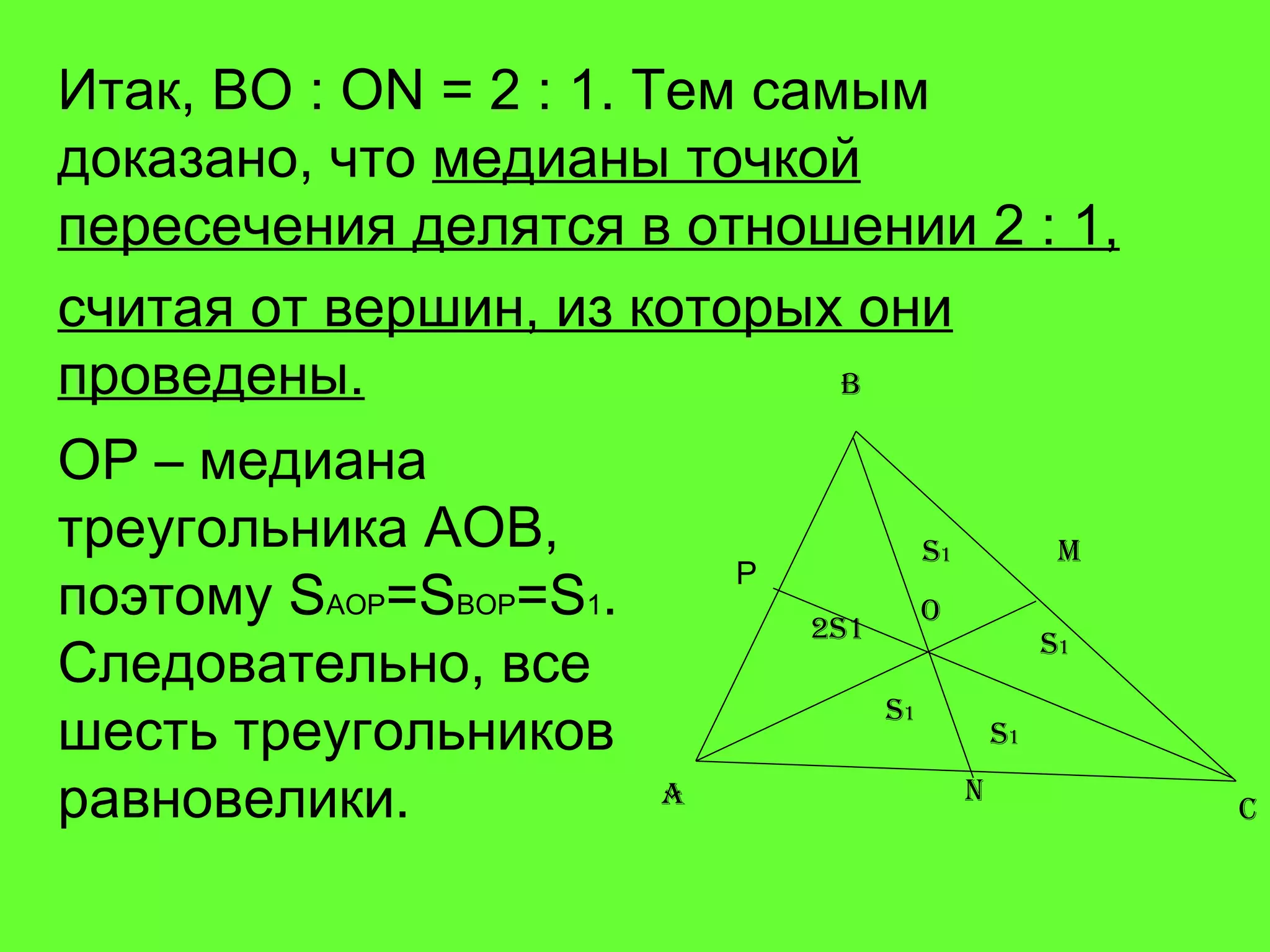
Документ рассматривает свойства медиан треугольника и приводит доказательства различных утверждений о них. Согласно теореме, медианы треугольника пересекаются в одной точке, делят его на шесть равновеликих треугольников и разделяются в отношении 2:1 от вершин треугольника. Также доказаны обратные утверждения о том, что отрезок, делящий треугольник на два равновеликих треугольника, является медианой.

1. Некоторые свойства медиан треугольника

2. Теорема. Медиана треугольника делит его на два равновеликих треугольника. Обратное утверждение : «Если отрезок, соединяющий вершину треугольника с точкой противоположной стороны, делит данный треугольник на два равновеликих треугольника, то этот отрезок является его медианой». Докажем, к примеру, обратное утверждение.

3. Доказательство I способ. Пусть ВМ – данный отрезок и S ABM = S BMC . Проведем высоту ВН треугольника. Тогда 2 S ABM = AM ∙В H и 2 S BMC = MC ∙ BH . Ясно, что AM ∙ BH = MC ∙ BH и АМ=МС. Следовательно, отрезок ВМ – медиана данного треугольника. H A B C M

4. II способ. 1. Пусть ВМ – данный отрезок и S ABM = S BMC . Отрезки AP и С Q – высоты треугольников АВМ и ВМС, проведенные к одной и той же стороне. 2. Так как S ABM = S BMC , то AP ∙ BM = CQ ∙ BM, откуда AP = CQ. 3. ∆ AMP = ∆ CMQ (по катету и острому углу). AM = CM . Следовательно, отрезок ВМ – медиана данного треугольника. A B C Q P M

5. Решим задачу . Пусть точка К – произвольная точка медианы BM треугольника ABC . Докажите, что S ABK +S MKC = S BKC + S AKM . Доказательство. KM - медиана треугольника AKC , поэтому S AKM = S MKC (1). A B C К M

6. BM - медиана треугольника ABC , следовательно, S ABM = S BMC (2) . Вычтем почленно из равенства (2) равенство (1) S AKM = S MKC : S ABM – S A К M = S BMC – S MKC . Получаем, что S ABK = S BKC .(3) A B C К M

7. Перепишем равенство (1) в виде: S MKC = S AKM и, сложив его почленно с равенством (3) S ABK = S BKC , получим требуемое: S ABK +S MKC = S BKC + S AKM . A B C К M

8. Теперь докажем два утверждения . Медианы треугольника пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, считая от вершин, из которых они проведены. Медианы треугольника, пересекаясь, делят его на шесть равновеликих треугольников.

9. Пусть AM и BN - медианы треугольника ABC , пересекающиеся в точке О.Через точку O проведем отрезок CP с концом P на стороне AB .Так как точка O лежит на медиане ON треугольника ABC , то S AON = S ONC = S 1 . A B C M N O P

10. Так как точка О лежит на медиане ОМ треугольника ВОС, то S BOM = S OMC = S 2 . Так как О – точка медианы BN , то S AOB = S BOC = 2S 2 . Ввиду того, что О – точка медианы АМ, S AOB = S А OC , то есть 2 S 2 = 2S 1 и S 2 = S 1 . A B C M N O S 1 P S 2 S 2 S 1

11. Значит, S AOC = S BOC , то есть отрезок CP - медиана треугольника ABC , следовательно, медианы треугольника пересекаются в одной точке . Треугольники BOC и CON имеют общую высоту, проведенную к сторонам BO и ON соответственно и S BOC : S CON = 2 : 1. A B C M N O Р S 1 S 1 S 1 S 1 2S1

12. Итак, BO : ON = 2 : 1. Тем самым доказано, что медианы точкой пересечения делятся в отношении 2 : 1, считая от вершин, из которых они проведены. OP – медиана треугольника АОВ, поэтому S AOP =S BOP =S 1 . Следовательно, все шесть треугольников равновелики. A B C M N O Р S 1 S 1 S 1 S 1 2S1