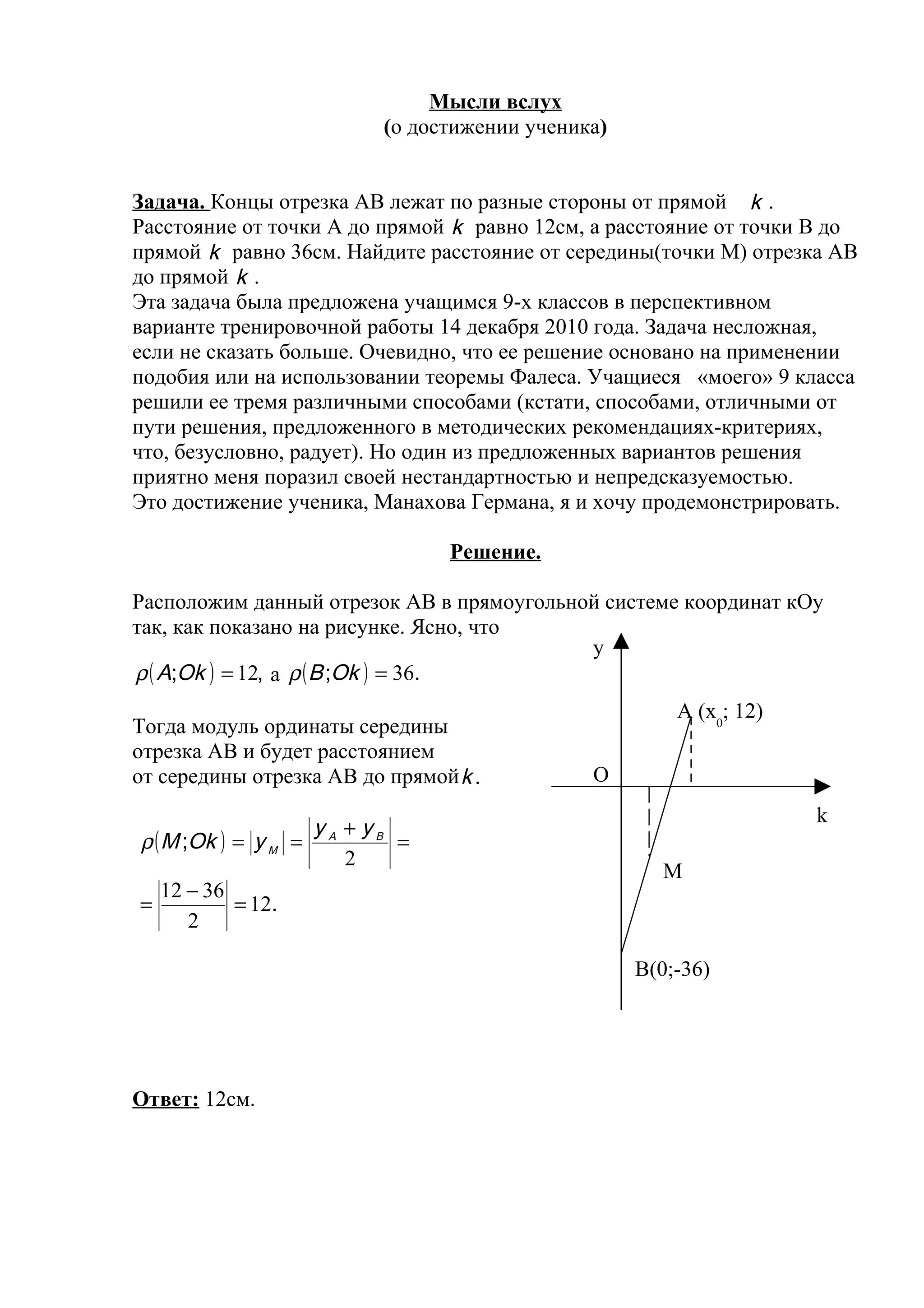
Документ описывает задачу по геометрии для учеников 9-х классов, связанную с расстоянием от середины отрезка до прямой. Учащиеся решили задачу тремя разными способами, один из которых оказался особенно оригинальным. Итоговое расстояние от середины отрезка до прямой составило 12 см.

1. Мысли вслух
(о достижении ученика)
Задача. Концы отрезка АВ лежат по разные стороны от прямой k .
Расстояние от точки А до прямой k равно 12см, а расстояние от точки В до
прямой k равно 36см. Найдите расстояние от середины(точки М) отрезка АВ
до прямой k .
Эта задача была предложена учащимся 9-х классов в перспективном
варианте тренировочной работы 14 декабря 2010 года. Задача несложная,
если не сказать больше. Очевидно, что ее решение основано на применении
подобия или на использовании теоремы Фалеса. Учащиеся «моего» 9 класса
решили ее тремя различными способами (кстати, способами, отличными от
пути решения, предложенного в методических рекомендациях-критериях,
что, безусловно, радует). Но один из предложенных вариантов решения
приятно меня поразил своей нестандартностью и непредсказуемостью.
Это достижение ученика, Манахова Германа, я и хочу продемонстрировать.
Решение.
Расположим данный отрезок АВ в прямоугольной системе координат кОу
так, как показано на рисунке. Ясно, что
y
ρ ( A;Ok ) = 12, а ρ ( B ;Ok ) = 36.
A (x0; 12)
Тогда модуль ординаты середины
отрезка АВ и будет расстоянием
от середины отрезка АВ до прямой k . O
k
y + yB
ρ ( M ;Ok ) = y M = A =
2
M
12 − 36
= = 12.
2
B(0;-36)
Ответ: 12см.