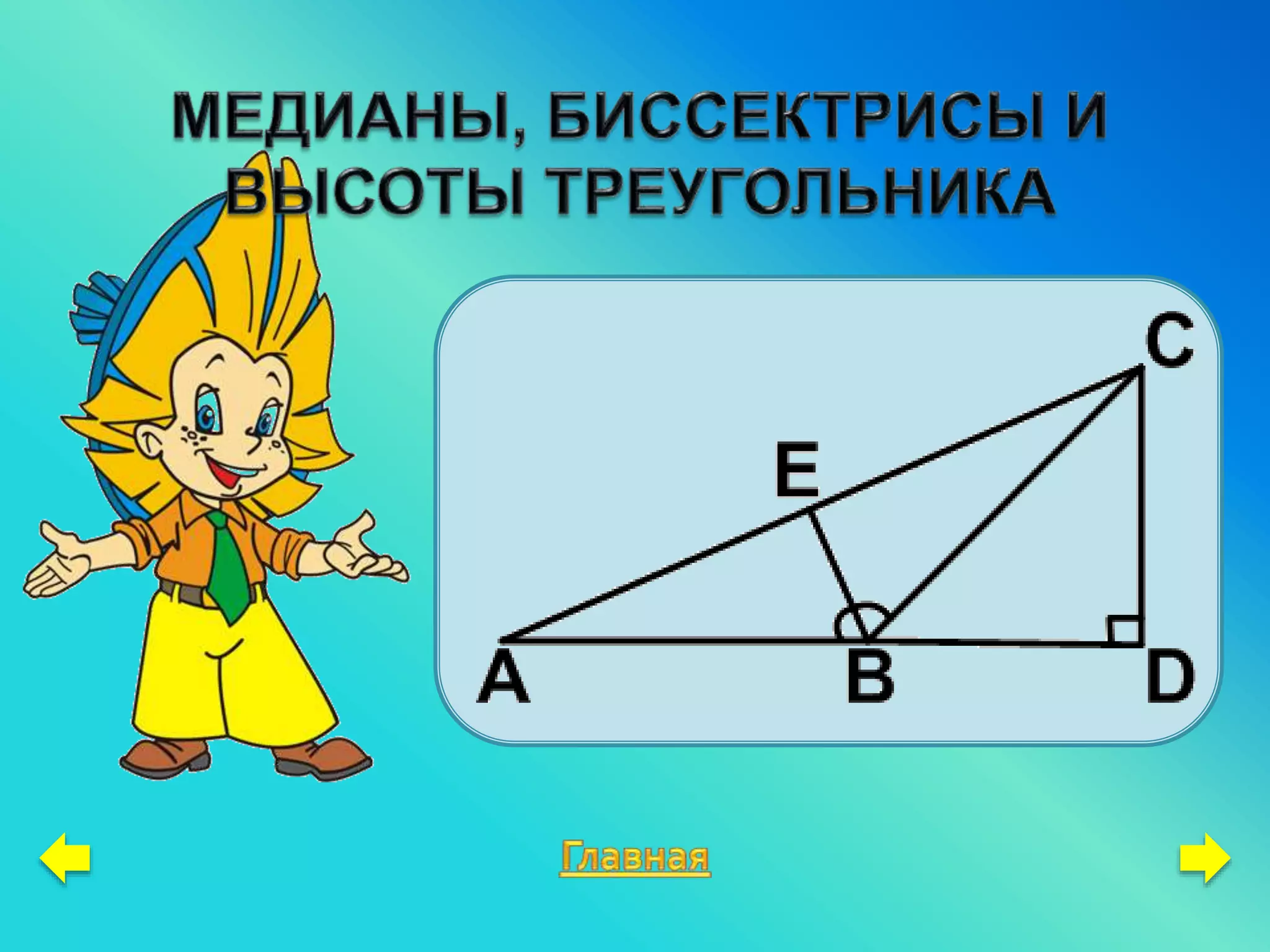
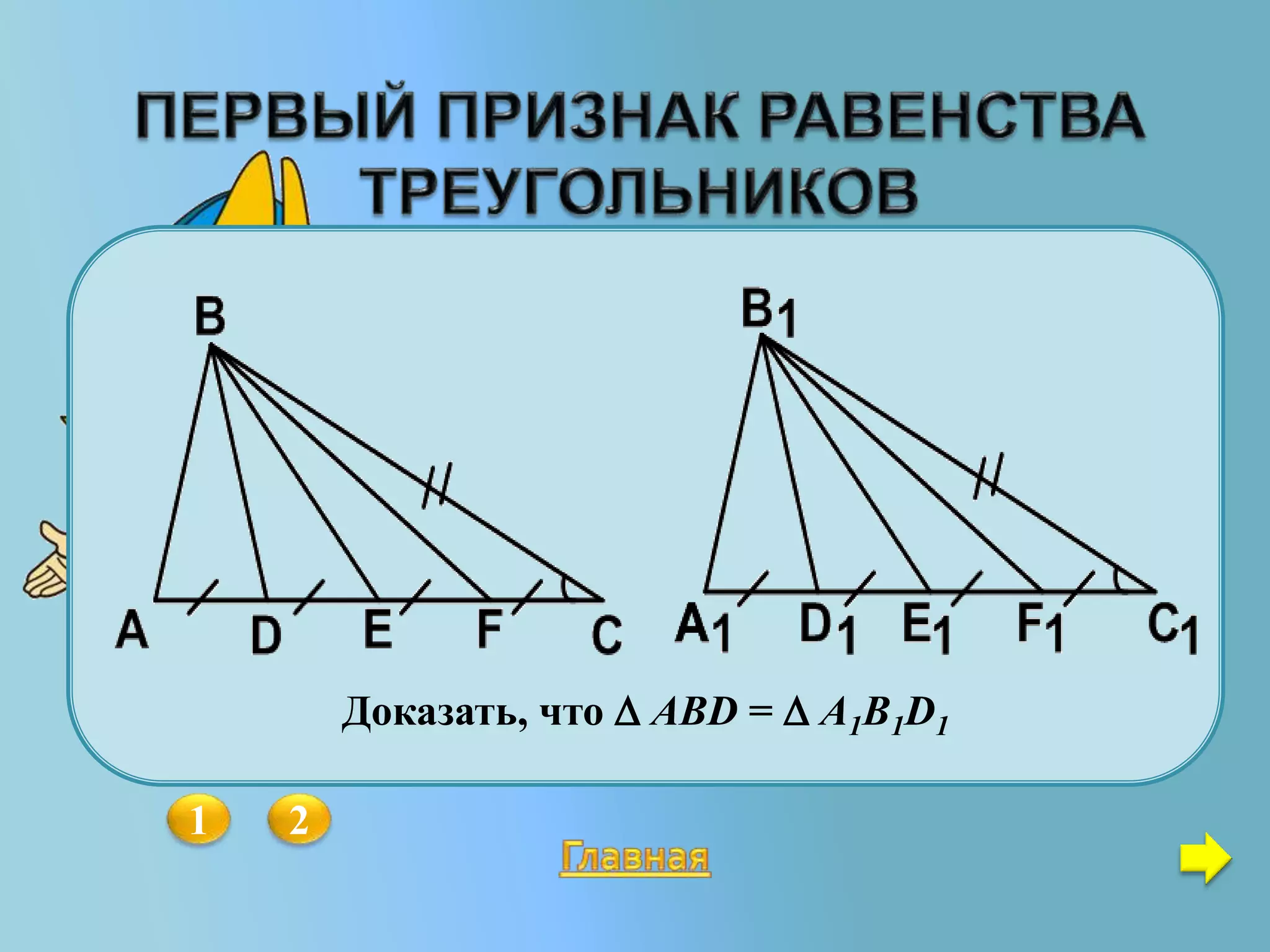
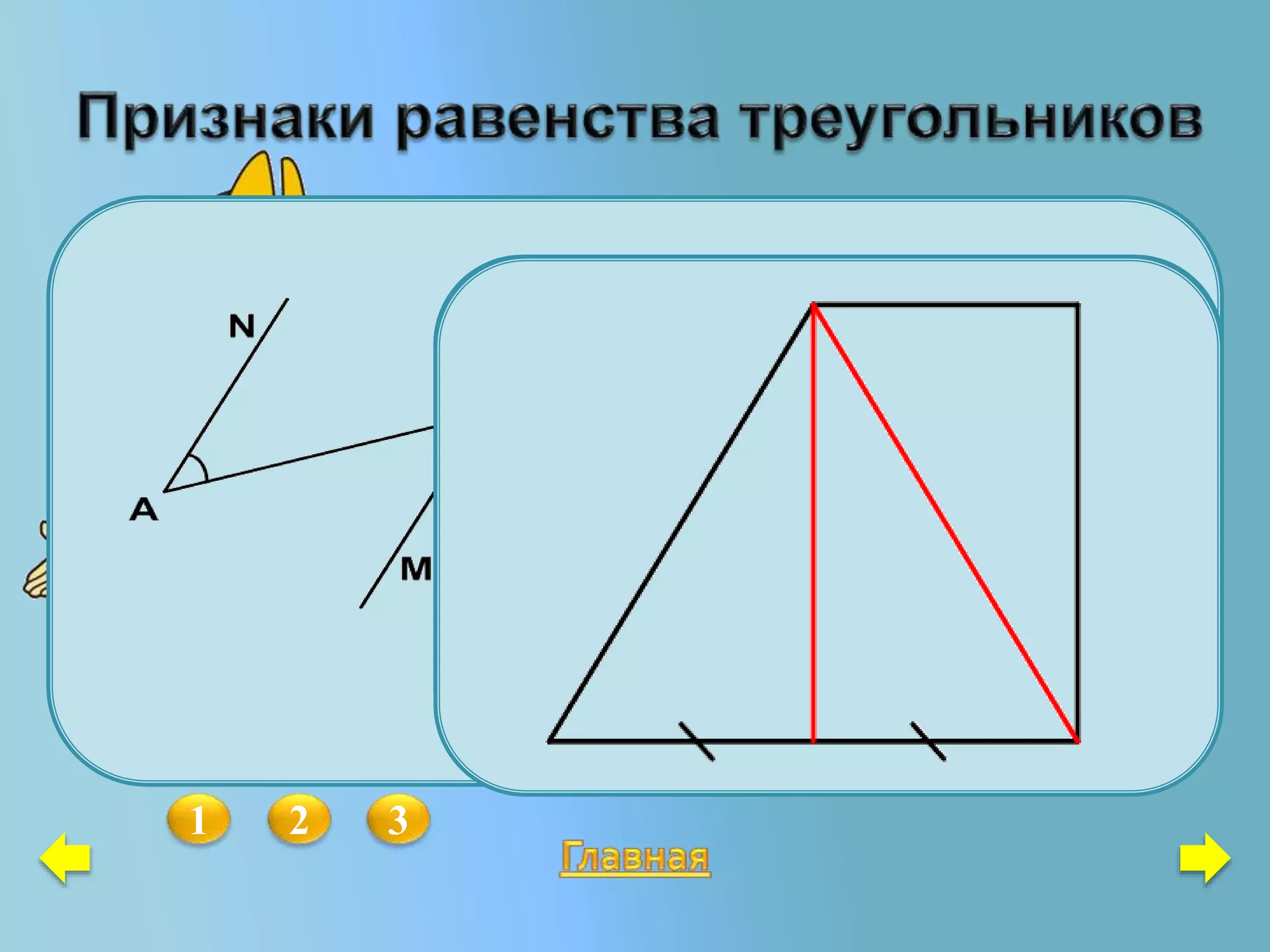
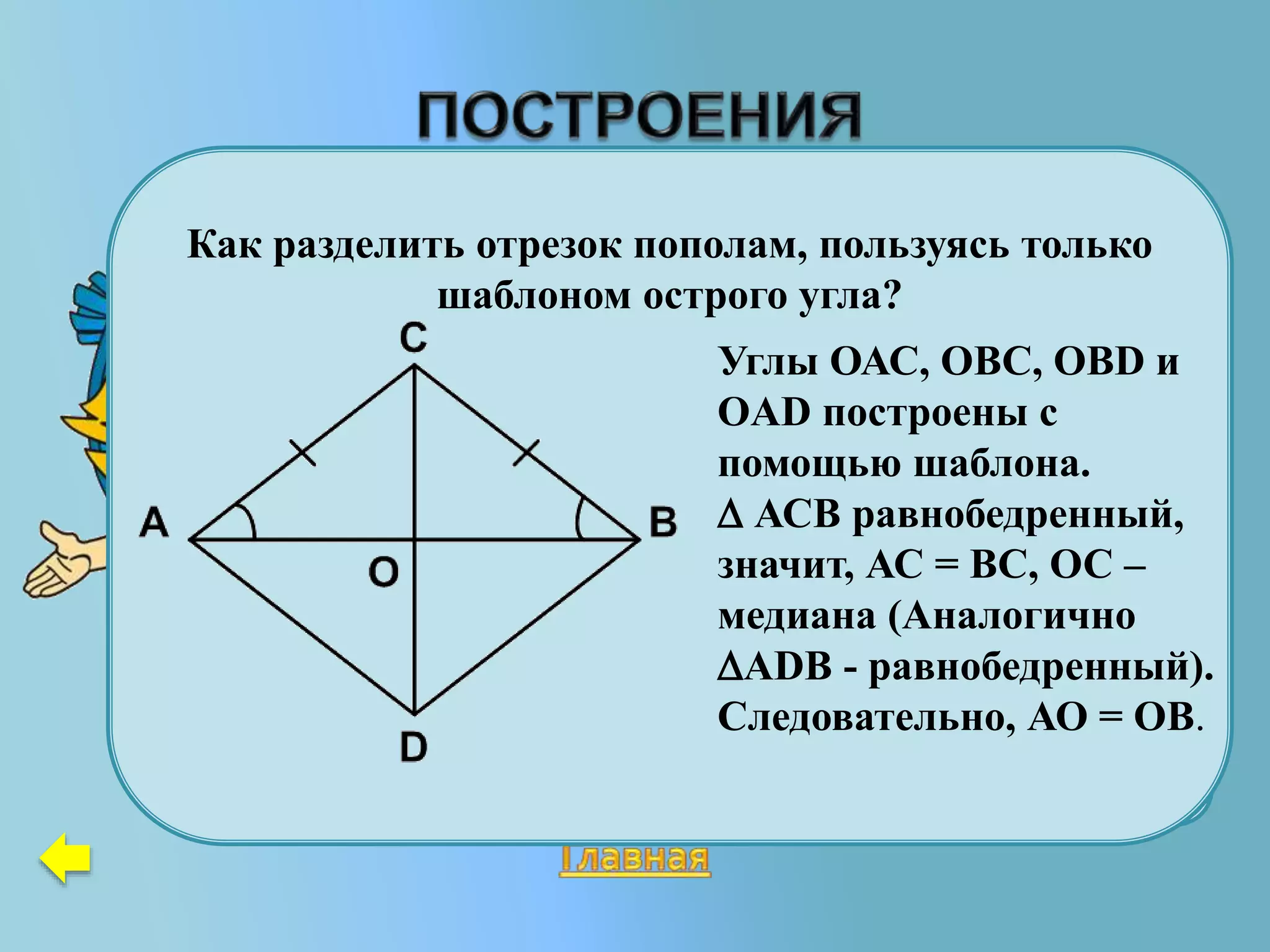
Документ содержит задачи и объяснения по геометрии, в частности, о равенстве треугольников и свойствах различных треугольников, таких как равнобедренные и равносторонние. Он включает в себя утверждения о медианах, биссектрисах, высотах и углах, а также примеры задач на нахождение равенства треугольников. Материал предназначен для учащихся 7-9 классов и содержит методические рекомендации и задачи для самостоятельного решения.