Документ содержит урок по математике, посвященный понятию площади криволинейной трапеции и её связи с интегралом. Рассматриваются определения, примеры и процесс вычисления площади криволинейной трапеции через пределы и интегралы. Также представлены задачи для самостоятельной работы по данной теме.

1. Площадь
криволинейной
трапеции
Креславская Е. М.,
учитель математики
ГБОУ средней школы №229
Адмиралтейского района
Санкт-Петербурга

2. Цель урока:
 закрепить понятие интеграла,
 связать его с площадью криволинейной
трапеции,
 рассмотреть частные случаи различных
криволинейных трапеций, в том числе
и таких, где нарушено условие
неотрицательности функции y = f(x).

3. Определение
криволинейной
трапеции

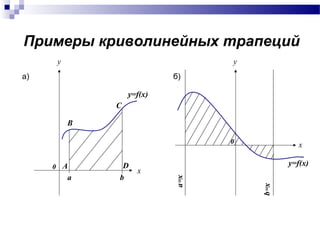
4. Пусть функция y=f(x) определена и
непрерывна на [a;b] , причем f(x)≥0.
Криволинейной трапецией называется
часть плоскости, ограниченная
графиком функции y=f(x), прямыми
x=a и x=b и отрезком [a;b] оси OX.

5. Примеры криволинейных трапеций
а) б)
B
C
DA
a b
y
x
0
y=f(x)
x=a
x=b
y
x0
y=f(x)

6. Площадь криволинейной трапеции
n
ab
x
−
=
Разделим отрезок AB
на n равных частей
a
y
x
0
b
y = f (x)
=xnx1 x2x0= xn-1…
и проведем через точки деления
прямые, параллельные оси OY,
рассмотрим ряд прямоугольников
с основаниями
и высотой f(xi ), i [0; n-1].
Получим ступенчатое тело.
x=a
x=b

7. Sступенчатого тела Sкриволинейной трапеции
 Пусть ∆ x→0
 Тогда Sступ. тела → Sкрив. трапеции
≈

8. Определение
интеграла

9. Интегралом от функции f(x) на [a; b]
называется предел площади
ступенчатого тела, построенного для
функции f(x) на [ a; b ], при условии,
что длина отрезка разбиения ∆ x→ 0.

10. Формула Ньютона-Лейбница
)()()( aFbFdxxf
b
a
−=∫

11. Пример:
Найти площадь криволинейной
трапеции, ограниченной графиками
функций: f (x) = x2
- 1, x = 1, x = - 1 и
осью OX.

12. Построение:
y
x
-1
y
x-1 1
y= - f(x)

13. 2 вариант
 S(x): y= x2
- 4
x= -2
x=2
Самостоятельная работа:
1 вариант
 S(x): y= - x2
x=1
x=2