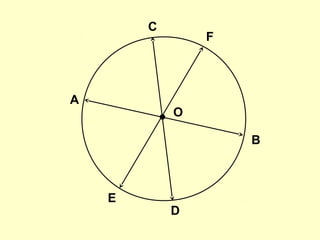
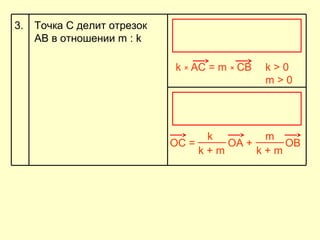
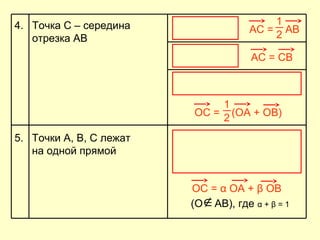
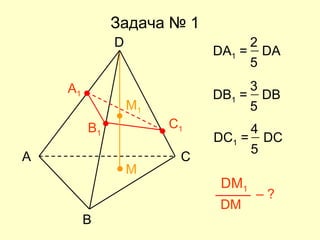
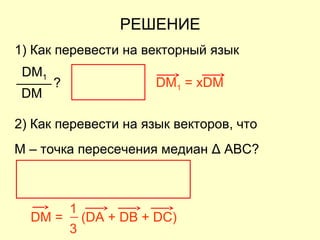
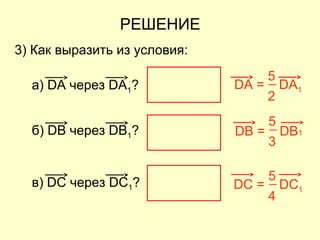
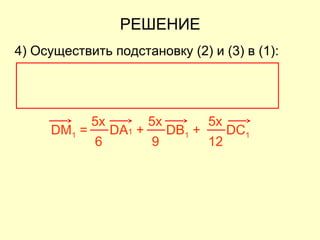
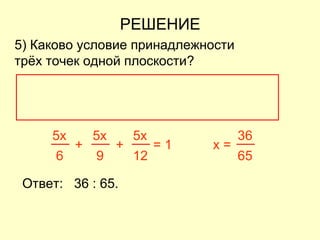
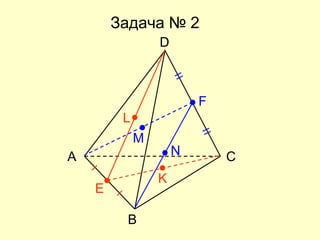
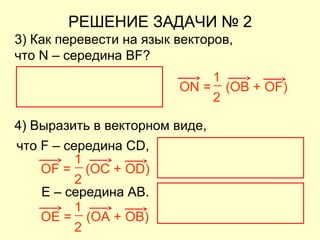
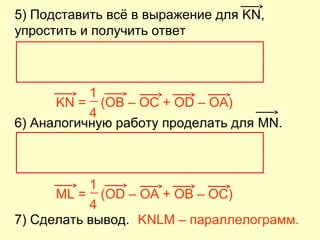
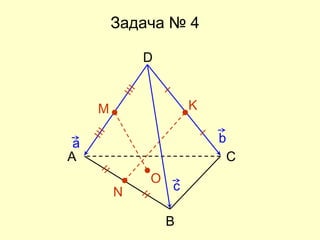
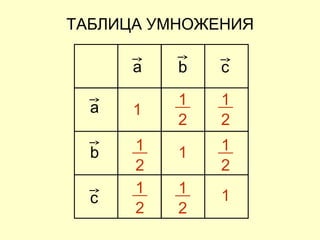
Документ представляет собой план открытого урока по математике для 10-го класса, посвященного векторному методу решения задач. В нем представлены задания на нахождение координат векторов, теории о скалярном произведении и условия перпендикулярности и коллинеарности векторов. Также рассматриваются задачи векторного представления геометрических утверждений и нахождения углов между прямыми.

1. ОТКРЫТЫЙ УРОК
ПО МАТЕМАТИКЕ В 10в
КЛАССЕ
ЛИЦЕЯ № 179
ТЕМА УРОКА
“ВЕКТОРНЫЙ МЕТОД
РЕШЕНИЯ ЗАДАЧ”
УЧИТЕЛЬ: ЗАКУЦКАЯ М.В.

2. “Не следует придавать значения
тому факту, что
алгебра и геометрия по видимости
различны. Алгебраические факты
есть факты геометрические,
которые доказаны”.
Омар Хайям

3. А
Е
В
D
С
F
О

4. ЗАДАНИЕ № 1
Даны точки: А (x1, y1, z1); B (x2, y2, z2).
Найти координаты вектора АВ и его длину.

5. ЗАДАНИЕ № 2
Даны векторы: m {m1, m2, m3}; n {n1, n2, n3}.
Записать для них:
а) определение
скалярного произведения векторов;
б) теорему
о скалярном произведении векторов.

6. ЗАДАНИЕ № 3
Записать условие перпендикулярности a и b,
и условие их коллинеарности, если
а {xa, ya, za}; b {xb, yb, zb}.

7. № На языке векторовНа геометрическом языке
Таблица перевода геометрических
утверждений на язык векторов
1. Точка С лежит на прямой
(отрезке) АВ
АС = k × АВ
2. АВСD - параллелограмм
АB = DС или BC = AD

8. 3. Точка С делит отрезок
АВ в отношении m : k
OC = OA + OB
k + m
k
k + m
m
k × АС = m × CB k > 0
m > 0

9. 4. Точка С – середина
отрезка АВ
AС = AВ2
1
AС = СВ
ОС = (ОA + ОВ)2
1
5. Точки А, В, С лежат
на одной прямой
ОС = α ОA + β ОВ
(О АВ), где α + β = 1∉

10. 6. Точки А, В, С лежат
в одной плоскости
ОD = α ОA + β ОВ + γ ОС
(О (АВС)), где α + β + γ = 1∉
7. Точка M – центроид ∆ АВС
MA + MB + MC = 0
ОM = (ОA + ОВ + OC)3
1

11. С
В
A
D
Задача № 1
5
DА1 = DA
2
5
DВ1 = DB
3
5
DС1 = DC
4
А1
С1В1
М1
М
DM
– ?
DM1

12. РЕШЕНИЕ
DM1 = xDM
DM = (DA + DB + DC)
3
1
1) Как перевести на векторный язык
DM
?
DM1
2) Как перевести на язык векторов, что
M – точка пересечения медиан Δ ABC?

13. РЕШЕНИЕ
3) Как выразить из условия:
а) DA через DА1?
б) DB через DB1?
в) DC через DC1?
2
DA = DA1
5
3
DB = DB1
5
DC = DC1
4
5

14. 4) Осуществить подстановку (2) и (3) в (1):
DM1 = DA1 + DB1 + DC1
6
5x
9
5x
12
5x
РЕШЕНИЕ

15. РЕШЕНИЕ
5) Каково условие принадлежности
трёх точек одной плоскости?
+ + = 1
6
5x
9
5x
12
5x
x =
65
36
Ответ: 36 : 65.

16. Задача № 2
С
В
A
D
F
Е
N
M
L
K

17. РЕШЕНИЕ ЗАДАЧИ № 2
1) Как перевести на язык векторов,
что KLMN – параллелограмм?
KN = ML
KN = ON – OK
2) Как представить KN в виде
разности двух векторов с концами
в точках N и K?

18. РЕШЕНИЕ ЗАДАЧИ № 2
3) Как перевести на язык векторов,
что N – середина BF?
ON = (OB + OF)
2
1
4) Выразить в векторном виде,
OF = (OC + OD)
2
1
OE = (OA + OB)
2
1
что F – середина СD,
E – середина АВ.

19. 5) Подставить всё в выражение для KN,
упростить и получить ответ
KN = (OB – OC + OD – OA)
4
1
7) Сделать вывод.
6) Аналогичную работу проделать для MN.
KNLM – параллелограмм.
ML = (OD – OA + OB – OC)
4
1

20. ЗАДАЧА № 3
Найти область значения функции:
2
361)( xxxxf −+−=

21. a

РЕШЕНИЕ ЗАДАЧИ № 3
2
231)( xxxxf −+−= { }
{ }3;1
2;1 2
b
xxxa


−−
3. Найти .b

4. При каких ?х ba

↑↑
6. Ответ.
5. При каких ?х ba

↑↓
2. Найти .a

b

b

1. Найти .)( fD

22. ЗАДАЧА № 4
В правильном тетраэдре DАВС точки
K, M, N – середины рёбер CD, AD, AB
соответственно. Точка О – центр ∆ABC.
Найдите угол между прямыми MO и KN.

23. Задача № 4
С
В
A
D
O
N
a b
с
M K

24. ТАБЛИЦА УМНОЖЕНИЯ
a
b
с
a b с
1
1
1
2
1
2
1
2
1
2
1
2
1
2
1

25. ПЛАН РЕШЕНИЯ
3. Выразить на векторном языке
М – середина АD.
2. Перевести на язык векторной алгебры
О – центр ∆ АВС (связать с точкой D).
10. Найти сos .ϕ 11. Ответ.
1. Представить MO в виде разности двух векторов
(связать с точкой D).
5. Выразить KN через DN и DK.
6. N – середина AB. 7. K – середина DC.
9. Найти: а) MO × KN, б) │MO│, в) │KN│.
4. Выразить МО через a, b, c.
8. KN – через a, b, c.

26. СПАСИБО ЗА ВНИМАНИЕ!