1. Òààìàãëàë øàëãàõ:
HYPOTHESIS
TESTING:

2. Статистик шалгуурууд
• Ихэнх өгөгдлүүд тохиолдлуудыг бүлэгт
хуваадаг.
Жишээ нь: өгөгдөлд эрэгтэйчүүд, эмэгтэйчүүд
эсвэл ялгаатай эмчилгээ хийлгэж байгаа
өвчтөнүүд эсвэл янз бүрийн бүс нутагт байрлах
компаниуд гэх мэт байж болох юм.
• Бүлэг дотор хувьсагчид ямар төлөв үзүүлж
байгааг хэрхэн тайлбарлах вэ?
• Бүлгүүдийн хооронд ямар нэг ялгаа байна уу?
Эдгээр асуултуудын хариултууд нь
хувьсагчдын төрлөөс: нэрлсэн, дараалсан,
интервал эсэхээс хамаарна.

3. Таамаглал шалгах
• Бүлгүүдийн эх олонлогийн талаарх үзэл
бодол, таамаглалыг бид статистикийн
таамаглалууд гэж нэрлэнэ.
• Эдгээр нь ердөө л нэг эсвэл олон эх
олонлогууд дахь хувьсагчийн шинж
чанарын тухай тодорхойлолтууд юм.
Статистикийн шалгуурт таамаглалыг бие
биенээ үгүйсгэсэн хоёр өрсөлдөх
таамаглалаар илэрхийлдэг.

4. Таамаглал шалгах
ТЭГ-ТААМАГЛАЛ (H0)
АЛЬТЕРНАТИВ-ТААМАГЛАЛ
(H1)
• Эх олонлогуудын тухай анхны таамаглал
бөгөөд, тэдгээрийн хооронд ялгаа байхгүй гэж
үздэг.
• Эх олонлогуудын тухай өрсөлдөх таамаглал
бөгөөд тэдгээрийн хооронд ялгаа байна гэж
үздэг.

5. Таамаглал (hypothesis)
• Тэг таамаглал нь бүх дундажууд нь
тэнцүү
H 0 : µ1 = µ 2 = ... = µ k
• Дор хаяж хоёр дундаж нь ялгаатай
H1 : µ 1 ≠ µ 2 ≠ ... ≠ µ k
5

6. Таамаглал шалгах
• Өрсөлдөгч таамаглалыг судалгааны таамаглал
гэж нэрлэх тохиолдол байдаг.
• Энэ таамаглалыг бид шалгахыг хүсч байгаа
бөгөөд хүлээгдэж буй үр дүн, таамаглалаар
энэхүү таамаглал нь биелнэ хэмээн хүлээж
байдаг.
• Харин тэг-таамаглалыг үгүйсгэх таамаглал гэж
нэрлэдэг.

7. Жишээ: Таамаглал
дэвшүүлэх
Шинээр оношлогдсон 2 төрлийн
чихрийн шижингийн үед A-эм, B-
эмийн нөлөөлөл ялгаатай юу?
(тийм/үгүй)?

8. (H0) :Тэг-таамаглал
A эм = B эм
(H1) : Өрсөлдөгч-таамаглал
A эм = B эм
– Хоёр талт таамаглал: энэ тохиолдолд ямар
нэг баталгаа өгөх боломжгүй
• A эм > B эм
– Нэг талт таамаглал: Хэрвээ та өмнө нь В
эмийг хэрэглэдэг байсан бол мэдээж муу үр
дүн болно.
• A эм < B эм
– Нэг талт таамаглал: Яг ижилхэн гэхдээ

9. Таамаглал шалгах
Таамаглал шалгах явцад хоёр төрлийн
алдаа гарч болно.
Шийдвэр H0 : Худал H 1 : Үнэн
HO-няцаах Чадал I-р төрлийн
(1 – β) алдаа (α)
H1-зөвшөөрөх II-р төрлийн 1- α
алдаа (β)

10. Ач холбогдолын түвшин
(signification level)
• Шалгуурын үед нэгдүгээр төрлийн алдаа
илүү чухалд тооцогдоно.
Эх олонлогуудын хооронд үнэхээр ялгаа
байхгүй байхад та өөрийн шалгуураас
үндэслэн ялгаа байгаа хэмээн буруу
дүгнэлтийг хийж байна.
• Иймэрхүү 1-р төрлийн алдааг шалгуурыг
хийхийн өмнө тодорхой хязгаар тавьж
хянадаг. Энэхүү тодорхой хязгаарыг ач
холбогдлын түвшин гэх ба (α)-аар
тэмдэглэдэг.

11. P- УТГА (Ач холбогдолын
түвшин)
• Анагаахын салбарт Р-утга<0.05
үнэн үед тэг-таамаглалыг
хүлээж авах ба энэ тохиолдолд
статистик ач холбогдол бүхий
ялгаатай байна.

12. Ач холбогдолын түвшин
(signification level)
• Өөрөөр хэлбэл тархалтын талаарх
үнэн магадлалын хувь (клиникд
ойролцоогоор 0.05 байх нь
тохиромжтойбайдаг) юм.
• Энэ нь тэг-таамаглалыг буруугаар
үгүйсгэх магадлалын таслах утга юм.
Хэрэв энэ утгаас доогуур байвал та
тэг-таамаглалыг үгүйсгэх болно

13. Хоёр бие даасан түүврийн
Хувь /
пропорц
Z test
P1 − P2
Z=
P1 (1 − P1 ) P2 (1 − P2 )
+
n1 n2
P1= Нэг дэх түүврийн хувь
P2= Хоёр дахь түүврийн хувь
n1= нэг дэх түүврийн хэмжээ
n2= хоёр дахь түүврийн хэмжээ
13

14. Z –ийн үр дүнг тайлбарлах
Z=? Z≥
1.96
• 1.96 бол ач холбогдлын
түвшин = 5% p=0.05
• 2.58 бол ач холбогдлын
түвшин = 1% p=0.01
14

15. Хоёр бие даасан түүврийн дундаж
T-test
x1 − x 2
t=
2 2
Sp Sp
+
n1 n 2
X 1= эхний бүлгийн дундаж утга
X 2 хоёр дахь бүлгийн дундаж утга
=
S p = нэгтгэсэн дисперс
2
15

16. (n1 − 1)S + (n 2 − 1)S 2
2
1
2
S P=
2
n1 + n 2 − 2
Хүснэгтийн t утгыг
• чөлөөний зэрэг
• ач холбогдлын түвшинд (1%
эсвэл 5%) харгалзаж сонгоно.
16

17. Жишээ
Эрүүл бүлэг Чихрийн шижин
өвчтэй бүлэг
•25 хүн • 17 хүн
•Цусны даралтын
дундаж
• Цусны даралтын
дундаж
=125 mm Hg =132 mmHg,
SD = 10 mm Hg SD= 12 mm Hg .
Ач холбогдлын түвшин 1%
17

18. БОДОЛТ
n 1 = 25 X 1 = 125 S1 = 12
n 2 = 17 X 2 = 132 S2 =11
H0 : µ 1 = µ 2 S
H1 : µ 1 ≠µ
S2 P =
(25 − 1)102 + (17 − 1)122
2 + 17 − 2 = 117.6
25
α = 0.01
(25 − 1) ⋅144 + (17 − 1) ⋅121
S P=
2
= 117.6
25 + 11 − 2
18

19. Хариулт
125 − 132
t= = −2.503
117.6 117.6
+
25 17
Хүснэгтийн t утга df = 40
1% -ийн ач холбогдлын түвшинд = 2.58
Тайлбар
Тооцооны t утга нь хүснэгтийн t утгаас бага
гарсан учир чихрийн шижинтэй ба эрүүл
бүлэг хүн амын цусны даралтын дундажийн
хооронд статистик ач холбогдол бүхий ялгаа
байхгүй байна. 19

20. Чөлөөний Магадлал (p value)
зэрэг
0.10 0.05 0.01
1 6.314 12.706 63.657
5 2.015 2.571 4.032
10 1.813 2.228 3.169
17 1.740 2.110 2.898
20 1.725 2.086 2.845
24 1.711 2.064 2.797
25 1.708 2.060 2.787
∞ 1.645 1.960 2.576
20

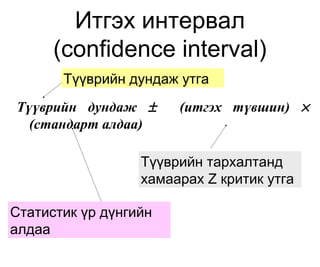
21. Итгэх интервал:
(confidence interval)
 Тархалтын итгэж болох далайцыг илтгэнэ.
 Итгэх интервал нь ажиглалтын явцад
хувьсагчийн тодорхой биш байдлыг харуулна.
 Статистик ач холбогдол (95% итгэх
интервалтай огтлолцохгүй утга, ач холбогдлын
түвшинг .05 тооцно)

22. Итгэх интервал
(confidence interval)
Түүврийн дундаж утга
Түүврийн дундаж ± (итгэх түвшин) ×
(стандарт алдаа)
Түүврийн тархалтанд
хамаарах Z критик утга
Статистик үр дүнгийн
алдаа

23. “Z” Итгэх түвшин
• Хэвийн нөхцөлд итгэх интервал (90%,
95%, 99%)
Итгэх
Z-утга
интервал
80% 1.28
90% 1.645
95% 1.96
98% 2.33
99% 2.58
99.8% 3.08
99.9% 3.27

24. Итгэх интервал
(confidence interval)
• Итгэх интервал нь таамаглал
шалгах шинжиллэгээнд зарим
мэдээлэл олгодог…

25. Хоёрдмол утгатай
таамаглал шалгах.
Ач холбогдолгүй 95% итгэх интервал
утга
150 151 152 153 154 155 156 157 158 159 160 161 162
163
Тэг-таамаглал: Дундаж = 150 БЖИ
Альтернатив таамаглал: Дундаж ≠ БЖИ
150
P-утга < .05

26. Хоёрдмол утгатай
таамаглал шалгах.
Ач холбогдолгүй 99% Итгэх интервал
утга
150 151 152 153 154 155 156 157 158 159 160 161 162
163
Тэг-таамаглал: Дундаж=150 БЖИ
Альтернатив таамаглал: Дундаж ≠ БЖИ
150
P-утга < .05

27. Тохиолдол:
Маш алдартай ресторанд хүлээлтийн цаг нь
хэвийн тархалттай байдаг ба дундажаар 2.25
цагийн хазайлттай байдаг байна.
– a. Ресторанд захиалга өгөхөөр хүлээсэн 20
хүн дундажаар 1.52 цаг хүүлсэн гэвэл 95%
итгэх интервалыг тооцоол.
– b. Ресторанд захиалга өгөхөөр хүлээсэн 32
хүн дундажаар 1.52 цаг хүлээсэн гэвэл 95%
итгэх интервалыг тооцоол.
– c. Түүврийн хэмжээ ихсэхэд итгэх интервалд
ямар нөлөөлөл гарч байна?

28. “Z” итгэх интервал
• Хэвийн нөхцөлд итгэх интервал (90%,
95%, 99%)
Итгэх
Z-утга
интервал
80% 1.28
90% 1.645
95% 1.96
98% 2.33
99% 2.58
99.8% 3.08
99.9% 3.27

29. Тохиолдол (a)
– a. Хүлээлтийн дундаж цаг 1.52, нийт 20 хүн
байсан гэвэл 95% итгэх интервал:
2.25
1.52 ± 1.96 = 1.52 ± 1.96(.33)
20
= 1.52 ± .65 = (.87, 2.17)

30. Тохиолдол (b, c)
– b. Хүлээлтийн дундаж цаг 1.52, нийт 32 хүн
байсан гэвэл 95% итгэх интервал:
2.25
1.52 ± 1.96 = 1.52 ± 1.96(.27)
32
= 1.52 ± .53 = (.99, 2.05)
c.Түүврийн хэмжээ нэмэгдэх тусам итгэх
интервал дахь нөлөөлөл хэр байна вэ?
Итгэх интервалын хэмжээ нарийн (Ижилхэн).

31. Нэг түүврийн дундажын тухай
таамаглал(σ)
• Таамаглал шалгах:
Ажиглалтын дундаж − 0
Z=
σ
n
• Итгэх интервал
σ
Ажиглалтын дундаж ± Zα/2 * ( )
n

32. Ñòàíäàðò òàðõàëòóóä
(òàñðàëòòàé ñàíàìñàðã¿é õýìæèãäýõ¿¿í)
o Æèãä òàðõàëò: Òóðøèëòûí ¿ð ä¿íã¿¿ä íü èæ èë ñàíàìñàðã¿é
õýìæ èãäýõ¿¿í¿¿äèéí òàðõàëò (íýã øèðõýã çîîñûã õàÿõ òóðøèëò, õî¸ð
øèðõýã çîîñûã õàÿõ òóðøèëò).
o Áèíîì òàðõàëò: Äýñ äàðààëñàí, õ¿ðýëöýõ¿éö õýìæ ýýíèé òóðøèëò á¿ðò
õî¸ð ýñðýã ¿çýãäëèéí àëü íýã íü èëðýõ áîëîìæ òîé ñàíàìñàðã¿é
õýìæ èãäýõ¿¿íèé òàðõàëò (çîîñûã õàÿàõàä ýñâýë òîîòîé òàëààðàà, ýñâýë
ñ¿ëäòýé òàëààðàà áóóíà).
o Áåðíóëëèéí òàðõàëò: Ýíý òàðõàëò íü Áèíîì òàðõàëòûí òóõàéí òîõèîëäîë
áºãººä òóðøèëòûí òîî 1 áàéíà.
o Ãèïåðãåîìåòðèéí òàðõàëò: Ýíý òàðõàëò íü áèíîì òàðõàëòòàé òºñòýé
òàðõàëò áºãººä äàâòàëòã¿é ò¿¿âýð ñóäàëãààíä õýðýãëýãääýã. Òîìîîõîí
ýõ îëîíëîãîîñ áàãà õýìæ ýýòýé ò¿¿âýð àâàõ òîõèîëäîëä áèíîì òàðõàëò
îéðîëöîîãîîð ãèïåðãåîìåòðèéí òàðõàëòòàé îéð áàéäàã.
o Ïîéññîíû òàðõàëò: Ñóäëàãäàæ áóé ¿çýãäýë ñóäëàãäàæ áóé õóãàöààíä
íýãýýñ îëîí óäàà ñàíàìñàðã¿é äàâòàìæ òàé èëðýõ ¿åä òàðõàëòûã íü
Ïîéññîíû òàðõàëòòàé ãýæ ¿çíý. Ò¿¿âðèéí õýìæ õ¿ðýëöýõ¿éö èõ áîëæ
ýý ,
ñàíàìñàðã¿é õýìæ èãäýõ¿¿íèé äóíäàæ õýìæ èãäýõ¿¿í/äèñïåðñèéí óòãà 7-
îîñ áàãà ¿åä ýíý òàðõàëò îéðîëöîîãîîð Áèíîì òàðõàëòàíä øèëæ äýã.
32

33. Ñòàíäàðò òàðõàëòóóä
(òàñðàëòã¿é ñàíàìñàðã¿é õýìæèãäýõ¿¿í)
• Õýâèéí òàðõàëò: Îëîíõ þìñ ¿çýãäëèéí
òàðõàëò õýâèéí áàéäàã áà ò¿¿âðèéí äóíäæèéí
òàðõàëòûã õàðóóëäàã.
-20 -10 0 10 20
68%
95.5% 33

34. Ñòàíäàðò òàðõàëòóóä
(òàñðàëòã¿é ñàíàìñàðã¿é õýìæèãäýõ¿¿í)
• Ý êñïîíåíöèàë òàðõàëò: Ýíý íü Ïîéññîíû òàðõàëòûí òóõàéí òîõèîëäîë
áºãººä ñóäëàãäàæáóé õóãàöààíä ñóäëàãäàæáóé ¿çýãäëèéí èëðýõ 0
áîëîìæ õàðóóëäàã.
èéã
• Ñòüþäåíòèéí òàðõàëò (t): Äèñïåðñ íü ¿ë ìýäýãäýõ, 30 õ¿ðòýë
òîîíû íýãæ áàãà ò¿¿âýðò èõýâ÷èëýí àøèãëàãääàã òàðõàëò (ýíý
òýé
òîõèîëäîëä ýíý òàðõàëòûí óòãà õýâèéí òàðõàëòûí óòãààñ
èë¿¿ íàðèéâ÷ëàëòàé áàéäàã).
-Èõ ò¿¿âðèéí õóâüä t òàðõàëò íü ñòàíäàðò õýâèéí òàðõàëòòàé îéðîëöîî
áàéíà.
-Ò¿¿âðèéí äèñïåðñ íü ìýäýãäýæáàéãàà áàãà ò¿¿âðèéã àøèãëàí t
òàðõàëòûí òóñëàìæ òàéãààð ýõ îëîíëîãûí äóíäæ ¿íýëýëòèéí õàðüöàíãóé
ûí
áîäèòîé óòãûã ãàðãàí àâ÷ áîëäîã.
• Õè-êâàäðàò òàðõàëò: Ò¿¿âðèéí òàðõàëòûã îíîëûí õýâèéí
òàðõàëòòàé çýðýãö¿¿ëýí ¿çýõýä ò¿ëõ¿¿ àøèãëàãääàã.
34

35. ÍÀÐÈÉÂ×ÈËÑÀÍ ÑÒÀÒÈÑÒÈÊ
¯Ç¯¯ËÝËÒ¯¯Ä/ÑÓÄÀËÃÀÀÍÛ ÀÐÃÓÓÄ
• Òàðõàëòûí ¿ë ìý ãäý ïàðàìåòðèéí ñòàòèñòèê
äý õ
¿íý ý àðãóóä
ëãý íèé
• Òààìàãëàë øàëãàõ òåõíèê¿¿ä
• Õ¿÷èí ç¿éë õîîðîíäûí õàìààðëûã øàëãàõ àðãóóä
Ò¿¿âðèéí ñòàòèñòèê íü ýõ îëîíëîãèéí èæ ïàðàìåòðèéí
èë
õóâüä ¯ÍÝ ËÒ íü áîëäîã.
ËÝ
¯íýëýëò äàðààõ øèíæ¿¿äèéí äîð õàÿæíýãèéã àãóóëæ
áàéâàë çîõèíî:
1 . Õàçàé ë ò ã¿ é áàé õ
2. ¯ ð àø è ãò àé áàé õ
3. Õàíãàë ò ò àé áàé õ
35

36. ¯ÍÝËÃÝÝÍÈÉ ÀÐÃÀ
¯íýëýëòèéí àâàõ óòãààñ íü õàìààðóóëàí äàðààõ
á¿ëýãò õóâààíà. ¯¿íä:
• Ö ýãýí ¿ íýë ãýýíè é àðãó ó ä (Õàìãèéí áàãà
êâàäðàòûí àðãà, õàìãèéí èõ ¿íýíèé õóâü á¿õèé
¿íýëãýýíèé àðãà, ìîìåíòûí ¿íýëãýýíèé àðãà)
• Òîäîðõîé óòãààð õýìæèäýã
• Èíò åðâàë ¿ íýë ãýýíè é àðãó ó ä (Èòãýìæëýãäñýí
èíòåðâàë)
• Òîäîðõîé õÿçãààðò õýìæèäýã
36

37. ÏÀÐÀÌÅÒÐ ÁÀ ÏÀÐÀÌÅÒÐ ÁÓÑ ØÈÍƯ¯Ð
• Ïàðàìåòð øèíæ¿¿ð: Ýõ îëîíëîãûí òàðõàëòûí ìºí ÷àíàðûí òàëààðõ
çàðèì òºñººëºë äýýð ñóóðèëäàã áóþó èõýâ÷èëýí õýâèéí òàðõàëòòàé
ãýæ ¿çäýã.Áàãà õýìæ ýýíèé ò¿¿âðèéí ìýäýýëýëä òóëãóóðëàí íýã
íºõöºëä ãàðãàí àâñàí óòãà íºãºº íºõöºëä ãàðãàí àâñàí óòãà õîîðîíäûí
ÿëãààã ñàéòàð òîäîðõîéëæ ÷àääàã òóë èë¿¿ ¿ð àøèãòàé ãýæ
¿çäýã.
• Ïàðàìåòð áóñ øèíæ¿¿ð: Çàðèì ñóäëàà÷ óã øèíæ ¿¿ðèéã îéëãîõ,
õýðýãëýõ íü õÿëáàð òóë áîäëîãîã¿é ¿éëäýëä ºðòºõ íü áàãà, öººí òîîíû
ñóóðü òºñººëºë õýðýãëýäýã òóë ºðãºí õ¿ðýýíä àøèãëàõ áîëîìæ òîé, ¿ð
àøãèéí õóâüä ïàðàìåòð øèíæ ¿¿ðèéí ¿ð ä¿íòýé áàðàã àäèë, îð÷èí ¿åä
õýðýãëýýíèé íºõöºë íü á¿ðäñýí ãýæ ¿çäýã (Colin Robson, 1993)
Àíõààðàõ ç¿éë: Òîî ìýäýýíèé ÷àíàð, ïðîãðàìì çýðãýýñ õàìààðàí
øèíæ¿¿ðèéã ñîíãîõäîî õÿíóóð õàíäàõ íü ç¿éòýé. Òîî áàðèìòûí
òàðõàëò õýâèéí áèø, ýðýìáýëýãäñýí áèø áîë ïàðàìåòð øèíæ¿¿ðèéã
àøèãëàõ íü ç¿éòýé.
37

38. ÏÀÐÀÌÅÒÐÈÉÍ ÁÓÑ ØÈÍƯ¯Ð: Õè
êâàäðàò øèíæ (Pearson chi square)
¿¿ð
• Õè êâàäðàò òåñò íü ñóäëàãäàæáóé þìñ ¿çýãäýëèéí
õîîðîíä:
– Ñóäëàãäàæáóé õ¿÷èí ç¿éë¿¿äèéí õîîðîãäûí ÿëãàà áàéãàà
ýñýõ,
– Òóõàéí õ ¿÷èí ç¿éëýýñ õàìààðàõ õàìààðàë áàéãàà ýñýõ
• Àíõààð
• ×àíàðûí ìýäýýíèé õóâüä àøèãëàäàã (nominal,
ordinal)
• Õàìààðàëûí õ¿÷èéã õýìæ äýãã¿é

40. ÏÀÐÀÌÅÒÐÈÉÍ ÁÓÑ ØÈÍƯ¯Ð: Õè
êâàäðàò øèíæ (Chi square)
¿¿ð
• SPSS ïðîãðàììä ¿ð ä¿íã òîîöîîëîõ

41. ÏÀÐÀÌÅÒÐÈÉÍ ÁÓÑ ØÈÍƯ¯Ð: Õè
êâàäðàò øèíæ (Chi square)
¿¿ð
Æèøýý
ªëºí öóñàí äàõü ñàõàðûí ººð÷ëºëò
¯ç¿¿ëýëò Õýâèéí IFG Äèàáåò
Õóâü ±95%CI Õóâü ±95%CI Õóâü ±95%CI
N 890 177 37
ßñ ¿íäýñ
Õàëõ 83.60 2.43 77.97 6.11 75.68 13.82
Êàçàê 2.02 0.92 5.08 3.24 2.70 5.23
Áóñàä 14.38 2.31 16.95 5.53 21.62 13.26
Áàéðøèë
Õîò 53.48 3.28 35.59 7.05 56.76 15.96
պ人 46.52 3.28 64.41 7.05 43.24 15.96

42. Õè êâàäðàò òåñò; Óðüäà÷ íºõöºë
1. Ä ¿ ¿ ë æ áó é ò ýã ò ààìàãë àë Í : ßñ ¿íäýñ, áàéðøèëààñ
ýâø 0
öóñàí äàõü ºëºí ñàõàðûí õýìæ õàìààðäàãã¿é. (ÿëãààã¿é
ýý
áóþó èæ èëõýí)
2. ªðñºë äºã÷ ò ààìàãë àë Í : ßñ ¿íäýñ, áàéðøèëààñ öóñàí äàõü
1
ºëºí ñàõàðûí õýìæ õàìààðäàã. (ÿëãààòàé)
ýý
3. Ñ àò è ñò è ê ø àë ãó ó ð: Õóâüñàã÷óóäûí õîîðîíäûí õàìààðëûã
ò
õàìãèéí èõ ¿íýíèé õóâü á¿õèé àðãàä ¿íäýñëýõ õè êâàäðàò
øàëãóóðààð ¿íýëýâ. Õàìààðëûí õ¿÷èéã Êðàìåðèéí V íýðýëñýí
õýìæ èãäýõ¿¿íýýð òîäîðõîéëîãäîíî.
4. Èò ãýõ ò ¿ âø è íã áóþó ¿íýëãýýíèé àëäààã 95 õóâü áàéõààð
òîîöñîí.
5. Ò ¿ ¿ âýð îë îíë îãûí ò àðõ àë ò -ûã (r-1)(c-1) ãýñýí ÷ºëººíèé çýðýã
á¿õèé Õè êâàäðàò òàðõàëòààð òàðõàíà ãýæ¿çíý.
6. Ø àë ãó ó ð ìó æè é ã ÷ ºë ººíè é çýðýã (df) áîëîí èòãýõ ò¿âøèíã
àøèãëàí ¿íýëñýí óòãàà õ¿ñíýãòèéí îíîëûí óòãàòàé õàðüöóóëàí
¿íýëñýí.
42

43. ÏÀÐÀÌÅÒÐÈÉÍ ÁÓÑ ØÈÍƯ¯Ð: Õè
êâàäðàò øèíæ (Chi square)
¿¿ð
SPSS-Output
Chi-Square Tests
Asymp. Sig.
Value df (2-sided)
Pearson Chi-Square 28,376a 14 ,013
Likelihood Ratio 30,183 14 ,007
Linear-by-Linear
5,599 1 ,018
Association
N of Valid Cases 399
a. 3 cells (10,0%) have expected count less than 5. The
minimum expected count is 2,83.
Symmetric Measures
Value Approx. Sig.
Nominal by Phi ,267 ,013
Nominal Cramer's V ,267 ,013
N of Valid Cases 399
a. Not assuming the null hypothesis.
b. Using the asymptotic standard error assuming the null
hypothesis. 43

44. ÏÀÐÀÌÅÒÐÈÉÍ ÁÓÑ ØÈÍƯ¯Ð: Õè
êâàäðàò øèíæ (Chi square)
¿¿ð
¯ð ä¿íã áè÷èõ
ªëºí öóñàí äàõü ñàõàðûí ººð÷ëºëò
¯ç¿¿ëýëò Õýâèéí IFG Äèàáåò P
Õóâü ±95%CI Õóâü ±95%CI Õóâü ±95%CI
N 890 177 37
ßñ ¿íäýñ 0.092
Õàëõ 83.60 2.43 77.97 6.11 75.68 13.82
Êàçàê 2.02 0.92 5.08 3.24 2.70 5.23
Áóñàä 14.38 2.31 16.95 5.53 21.62 13.26
Áàéðøèë 0.000
Õîò 53.48 3.28 35.59 7.05 56.76 15.96
պ人 46.52 3.28 64.41 7.05 43.24 15.96
P<0.05 or P>0.05 P<0.001

45. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: t
ñòàòèñòèê
• One Sample T- òåñò
– Õóâüñàõ õýìæ èãäýõ¿¿íèé äóíäàæ óòãûã òîäîðõîé íýã
òîãòìîë òîî õàðüöóóëàõ
• Independent-Sample T- òåñò
– Äóíäàæ õýìæ èãäýõ¿¿í¿¿äèéí 2 ãðóïïûí àæèãëàëòûí
óòãóóäûã õàðüöóóëäàã
• Paired Sample T- òåñò
– Íýã á¿ëýãò áàéãàà 2 õóâüñàã÷èéí Ò-øàëãóóðûí
¿íýëãýýã òîîöîæ ãàðãàäàã. Ýíý íü àæèãëàëò á¿ðèéí 2
õóâüñàã÷èéí óòãûí ÿëãààã áîäîæ äóíäàæ èéí òýãýýñ
ÿëãàãäàõ ÿëãààíû òåñòèéã õèéíý
45

46. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: One
Sample T- òåñò
• “ One Sample t” øèíæ¿¿ðèéã äàðààõ
òîõèîëäîëä àøèãëàäàã
– Ñóäëàãäàæ áóé ¿ç¿¿ëýëòèéí íîðì, íîðìàòèâ
¿ç¿¿ëýëòòýé õàðüöóóëàõàä
• Æèøýý: 2-ð õýëáýðèéí ÷èõðèéí øèæ ºâ÷òýéèí
õ¿ì¿¿ñèéí BMI õýâèéí áàéãàà ýñýõèéã òîãòîîõ
– Òóõàéí ¿ç¿¿ëýëòèéí áóñàä îðîí, ºìíº õèéãäñýí
ñóäàëãààíû ¿ð ä¿íòýé õàðüöóóëàõ
• Õàëäâàðò ºâ÷íèé òàðàëòûí ñóäàëãààíû ¿ð ä¿íã ºìíº
õèéãäñýí ñóäàëãààíû ¿ð ä¿íòýé õàðüöóóëàõ
46

47. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: One
Sample T- òåñò
Тэг-таамаглал H0: µ=µ0
Альтернатив таамаглал H1: µ≠µ0
y −µ
t = 0
t-шинжүүр s
n
Шийдвэр: няцаах H0 хэрвээ |t|>tα/2,n-1
47

48. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: One
Sample T- òåñò
• Ä â ø ¿ ¿ ë æ á ó é ò ý ã ò à à ìà ã ë à ë Í : Ñóäëàãäàæ áóé
ý 0
õýìæèãäýõ¿¿í òîäîðõîé íýã òîãòìîë /óòãà/ òîîòîé
òýíö¿¿ áóþó ÿëãààã¿é
• ªð ñº ë ä º ã ÷ ò à à ìà ã ë à ë Í:
1 Ñóäëàãäàæ áóé
õýìæèãäýõ¿¿í òîäîðõîé íýã òîãòìîë /óòãà/ òîîíîîñ
ÿëãààòàé
• Ñ à ò è ñò è ê ø à ë ã ó ó ð : Õóâüñàã÷óóäûí õîîðîíäûí
ò
ÿëãààã t ñòàòèñòèê øàëãóóðààð ¿íýëýâ.
• Èò ã ý õ ò ¿ â ø è íã áóþó ¿íýëãýýíèé àëäààã 95 õóâü
áàéõààð òîîöñîí.
• Ò ¿ ¿ â ý ð îë îíë îã ûí ò à ð õ à ë ò -ûã (n-1; α) ãýñýí
÷ºëººíèé çýðýã á¿õèé Ñòüþäåíòèéí t òàðõàëòààð
òàðõàíà ãýæ ¿çíý.
• Ø à ë ã ó ó ð ìó æ è é ã ÷ º ë º º íè é ç ý ð ý ã (df) áîëîí èòãýõ
ò¿âøèíã àøèãëàí ¿íýëñýí óòãàà õ¿ñíýãòèéí îíîëûí
óòãàòàé õàðüöóóëàí ¿íýëñýí. 48

49. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: One
Sample T- òåñò
• One Sample t- òîîöîîëîõ (SPSS)
49

50. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: One
Sample T- òåñò
• One Sample t- òîîöîîëîõ (SPSS)
50

51. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: One
Sample T- òåñò
• Æèøýý: Ãàð àðãààð àëò îëáîðëîã÷ èðãýäèéí äóíä ìºíãºí
óñíû õîðäëîãûí ò¿âøèíã òîãòîîõ ñóäàëãààã ÿâóóëñàí.
Øýýñíèé ñîðüöîíä ìºíãºí óñíû ò¿âøèí òîäîðõîéëæýý.
(Øýýñýí äýõü ìºíãºí óñíû àãóóëàìæèéí õýâèéí õýìæýý
2.5mg/g)
• H0: µ=2.5 áóþó äýâø¿¿ëæ áóé òýã òààìàãëàë íü: Ãàð
àðãààð àëò îëáîðëîã÷èä ìºíãºí óñíû õîðäëîãîä ºðòººã¿é
áóþó ìºíãºí óñíû àãóóëàìæ õýâèéí õýìæýýòýé áàéãàà
• H1: µ≠2.5 áóþó àëüòàðíàòèâ òààìàãëàë íü: Ãàð àðãààð
àëò îëáîðëîã÷èä ìºíãºí óñíû õîðäëîãîä ºðòñºí áóþó ìºíãºí
óñíû àãóóëàìæ õýâèéí õýìæýýíýýñ èõýññýí

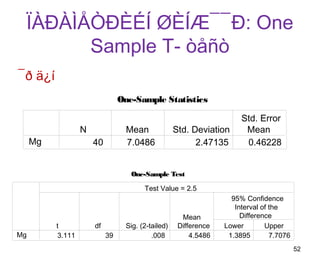
52. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: One
Sample T- òåñò
¯ð ä¿í
One-Sample Statistics
Std. Error
N Mean Std. Deviation Mean
Mg 40 7.0486 2.47135 0.46228
One-Sample Test
Test Value = 2.5
95% Confidence
Interval of the
Mean Difference
t df Sig. (2-tailed) Difference Lower Upper
Mg 3.111 39 .008 4.5486 1.3895 7.7076
52

53. Өвчтөн дугаар Өндөр (см)-y Жин (кг)-y2
1 178 101.7
2 170 97.1
3 191 114.2
4 179 101.9
5 182 93.1
6 177 108.1
7 184 85
8 182 89.1
9 179 98.8
10 183 97.8
11 - 78.7
12 172 77.5
13 183 102.8
14 169 81.1
15 177 102.1
16 180 112.1
17 184 89.7

54. Бодолт.
∑Y=481.5
∑y2=14627.74
Тэг-таамаглал H0: µ=28.4
Альтернатив таамаглал H1: µ≠28.4
t-шинжүүр
y − µ0 30.093 − 28.4
t= = = 2.23
s 3.037
n 16
Шийдвэр: няцаах H0 хэрвээ |t|>t0.025,15=2.131
Дүгнэлт: Хэрвээ t шинжүүр нь дээрх нөхцөлд үнэн
(2.23>2.131) байгаа учраас H0 таамаглалыг няцаах ба нийт
өвчтөнүүдийн BIM нь өмнөх хэмжилтийн үр дүнгээс
ялгаатай байна.

56. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð:
Independent-Sample T- òåñò
Àøèãëàõ òîõèîëäîë
• 2 á¿ëãèéí äóíäàæèéí õàðüöóóëàõàä
àøèãëàäàã
– Òîõèîëäîë õÿíàëòûí ñóäàëãàà (Case-control
study)
– Урт хугацааны ажиглалт судалгаа
(Longitudinal study)
56

57. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð:
Independent-Sample T- òåñò
Тэг-таамаглал H0: µ1=µ2
Альтернатив таамаглал H1: µ1≠µ2
y1 −y 2
t=
t-шинжүүр 2 1 1
sp ( + )
n1 n2
Шийдвэр: няцаах H0 хэрвээ |t|>tα/2,N-1

59. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð:
Independent-Sample T- òåñò
59

60. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð:
Independent-Sample T- òåñò
Æèøýý:
• H0: µäèàáåò=µýð¿¿ë áóþó äýâø¿¿ëæáóé òýã òààìàãëàë íü:
×èõðèéí øèæ ºâ÷òýé õ¿ì¿¿ñ, ýð¿¿ë õ¿ì¿¿ñèéí Cholesterol,
èí
Triglycerides, Glucose-ûí õýìæ èæ
ýý èëõýí
• H1: µäèàáåò ≠ µýð¿¿ë áóþó àëüòàðíàòèâ òààìàãëàë íü:
×èõðèéí øèæ ºâ÷òýé õ¿ì¿¿ñ, ýð¿¿ë õ¿ì¿¿ñèéí Cholesterol,
èí
Triglycerides, Glucose-ûí õýìæ ººð áóþó ÿëãààòàé
ýý

61. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð:
Independent-Sample T- òåñò
¯ð ä¿í
Group Statistics
Std. Error
diabits N Mean Std. Deviation Mean
Glucose Эрүүл 1067 4.7046 .98089 .03003
Өвчтэй 37 8.8824 2.64754 .43525
Cholesterol Эрүүл 655 4.7406 .58357 .02280
Өвчтэй 28 4.9271 .64407 .12172
Triglycerides Эрүүл 863 1.7070 1.14920 .03912
Өвчтэй 30 2.2087 1.13045 .20639
61

62. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð:
Independent-Sample T- òåñò
¯ð ä¿í
Independent Samples Test
Levene's Test for
Equality of Variances t-test for Equality of Means
95% Confidence
Interval of the
Mean Std. Error Difference
F Sig. t df Sig. (2-tailed) Difference Difference Lower Upper
Glucose Equal varianc es
98.448 .000 -23.199 1102 .000 -4.17781 .18008 -4.53116 -3.82447
assumed
Equal varianc es
-9.576 36.343 .000 -4.17781 .43629 -5.06235 -3.29327
not assumed
Cholesterol Equal varianc es
1.392 .238 -1.650 681 .100 -.18656 .11310 -.40863 .03551
assumed
Equal varianc es
-1.507 28.927 .143 -.18656 .12384 -.43986 .06674
not assumed
Triglycerides Equal varianc es
2.134 .144 -2.352 891 .019 -.50171 .21332 -.92038 -.08305
assumed
Equal varianc es
-2.388 31.120 .023 -.50171 .21007 -.93008 -.07335
not assumed

63. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð:
Independent-Sample T- òåñò
¯ð ä¿íã áè÷èõ
diabits control
Var Std. Std. t P
Mean Deviatio Mean Deviatio
n n
Glucose 8.882 2.648 4.705 0.981 -23.20 0.000
Cholesterol 4.927 0.644 4.741 0.584 -1.65 0.100
Triglycerides 2.209 1.130 1.707 1.149 -2.35 0.019

64. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð:
Independent-Sample T- òåñò
¯ð ä¿íã áè÷èõ
diabits control
Var Std. Std. P
Mean Mean
Deviation Deviation
Glucose 8.882 2.648 4.705 0.981 0.000
Cholesterol 4.927 0.644 4.741 0.584 0.100
Triglycerides 2.209 1.130 1.707 1.149 0.019
diabits control
Var Std. Std. P
Mean Mean
Deviation Deviation
Glucose 8.882 2.648 4.705 0.981 <0.001
Cholesterol 4.927 0.644 4.741 0.584 >0.05
Triglycerides 2.209 1.130 1.707 1.149 <0.05

65. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð:
Paired-Samples T- tåst
• H0: di = Xi1 – Xi2 =0 vs H1: di = Xi1 – Xi2 ≠ 0
• Paired Samples t ñòàòèñòèê øèíæ¿¿ð
t = d sd( n )
• H0: di = Xi1 – Xi2 =0 vs H1: di = Xi1 – Xi2 < 0
ýñâýë di = Xi1 – Xi2 > 0
• Confidence interval for Mean of Paired
Differences
d ± t n −1,1−α / 2 sd / n
65

67. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: Paired-
Samples T- tåst
67

68. ÏÀÐÀÌÅÒÐÈÉÍ ØÈÍƯ¯Ð: Paired-
Samples T- tåst
• ¯ð ä¿í
Paired Samples Statistics
Std. Error
Mean N Std. Deviation Mean
Pair I õàâòãàéí øóëóóí
11.2506 294 1.00826 .05880
1 õýì æ ýýñ
I õàâòãàéí
13.1763 294 .75877 .04425
õº í äëº í õýì æýýñ
Paired Samples Test
Paired Differenc es
95% Confidenc e
Interval of the
Std. Error Differenc e
Mean Std. Deviation Mean Lower Upper t df Sig. (2-tailed)
Pair I õàâòãàéí øóëóóí
1 õýì æ ýýñ - I õàâòãàéí -1.92568 1.19175 .06950 -2.06247 -1.78889 -27.706 293 .000
õº í äëº í õýì æýýñ
68

73. Øèíæ ¿¿ðèéí ñòàòèñòèê à÷ õîëáîãäîë áà
ïðàêòèê (àãóóëãûí) à÷ õîëáîãäîë
Àíõààðàõ ç¿éë:
• Ñòàòèñòèê à÷ õîëáîãäëûã øàëãàõààñ ãàäíà
ïðàêòèê à÷ õîëáîãäëûã íÿãòëàõ. Ãîë áýðõøýýë
íü ñòàòèñòèê à÷ õîëáîãäîë íü òóõàéí íºëººíèé
õýìæ ýý õèð ÷óõàë âý? ãýäýãò óÿëäààã¿é
áàéäàãò îðøäîã. Õàðèí ñàíàìñàðã¿é õ¿÷èí ç¿éëä
óã íºëºº òºäèéëºí õàìààòàé áóñ ãýäãèéã
õàðóóëäàãààðàà ë à÷ õîëáîãäîëòîé õýìýýí
òîîöîãääîã.
• Ñòàòèñòèê à÷ õîëáîãäîëòîé ¿ð ä¿í ãàðàõ
ìàãàäëàë ò¿¿âðèéí õýìæ íýìýãäýõèéí õèðýýð
ýý
ºñäºã áîëîâ÷ õàìãèéí èõäýý 0.05 áóþó 1/20
áàéõûã à÷ õîëáîãäîë ºíäºðòýé õýìýýí òîîöäîã.
73

74. Àíõààðàõ ç¿éë:
• Ñòàòèñòèê à÷ õîëáîãäëûã 1-ð òºðëèéí
àëäàà õèéõ ¿çýãäëèéí ìàãàäëàëààð
õýìæ äýã. Òèéìýýñ øèíæ ¿¿ðèéã à÷
õîëáîãäîë ºíäºðòýé áàéëãàíà ãýäýã íü òýã
òààìàãëàëûã ¿ã¿éñãýõ ýðñäëèéã áàãà
áàéëãàíà ãýñýí ¿ã.
• Øèíæ ¿¿ðèéí õ¿÷èí ÷àäàë íü òýã
òààìàãëàëûã çºâ ¿ã¿éñãýõ ¿çýãäëèéí
ìàãàäëàëààð òîäîðõîéëîãääîã.

75. Анхаарал хандуулсанд
баярлалаа.