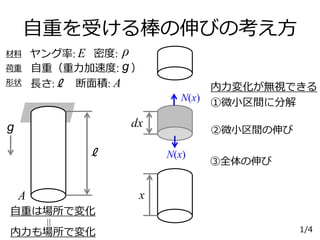
【材料力学】自重を受ける棒の伸び

1.
自重を受ける棒の伸び

2.
自重を受ける棒の伸びの考え方 g A ℓ 自重（重力加速度: ） Eヤング率: 長さ: ℓ断面積: A 材料荷重形状 ρ密度: g x dx ③全体の伸び ②微小区間の伸び ①微小区間に分解内力変化が無視できる N(x) N(x) 自重は場所で変化内力も場所で変化＝ 1/4

3.
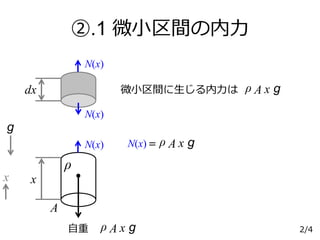
②.1 微小区間の内力 ρ Ax g xx N(x) N(x) dx N(x)＝ ρ A x g N(x) 自重微小区間に生じる内力は ρ A x g A g ρ 2/4

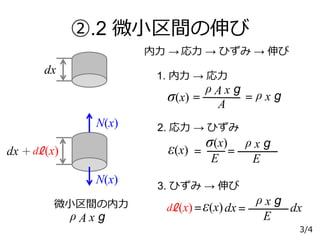
4.
②.2 微小区間の伸び dx 1.内力 → 応力 2. 応力 → ひずみ 3. ひずみ → 伸び内力 → 伸び応力 → ひずみ → ℓd (x)＝ε(x)dx ε(x) ＝ E σ(x) ＝ E ρ x g ＝ E ρ x g dx dx ℓd (x)＋ N(x) N(x) 微小区間の内力 ρ A x g σ(x) ＝ A ＝ ρ x g ρ A x g 3/4

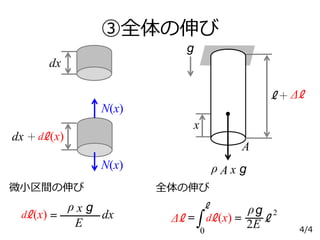
5.
③全体の伸び ℓd (x)＝ E ρ xg dx dx ℓd (x)＋ N(x) N(x) 微小区間の伸び g A ℓ Δℓ＋ ρ A x g x 全体の伸び＝Δℓ 0 ℓd (x) ℓ ＝ 2E ρg ℓ 2 dx 4/4

【材料力学】自重を受ける棒の伸び

More Related Content

What's hot

More from Kazuhiro Suga

【材料力学】自重を受ける棒の伸び

Editor's Notes