1. 真のモデルを含まない
パラメトリックモデル族に対する
ベイズ予測の漸近評価
宮 希望
須子 統太
安田 豪毅
松嶋 敏泰
早稲田大学

2. 研究背景
No.1
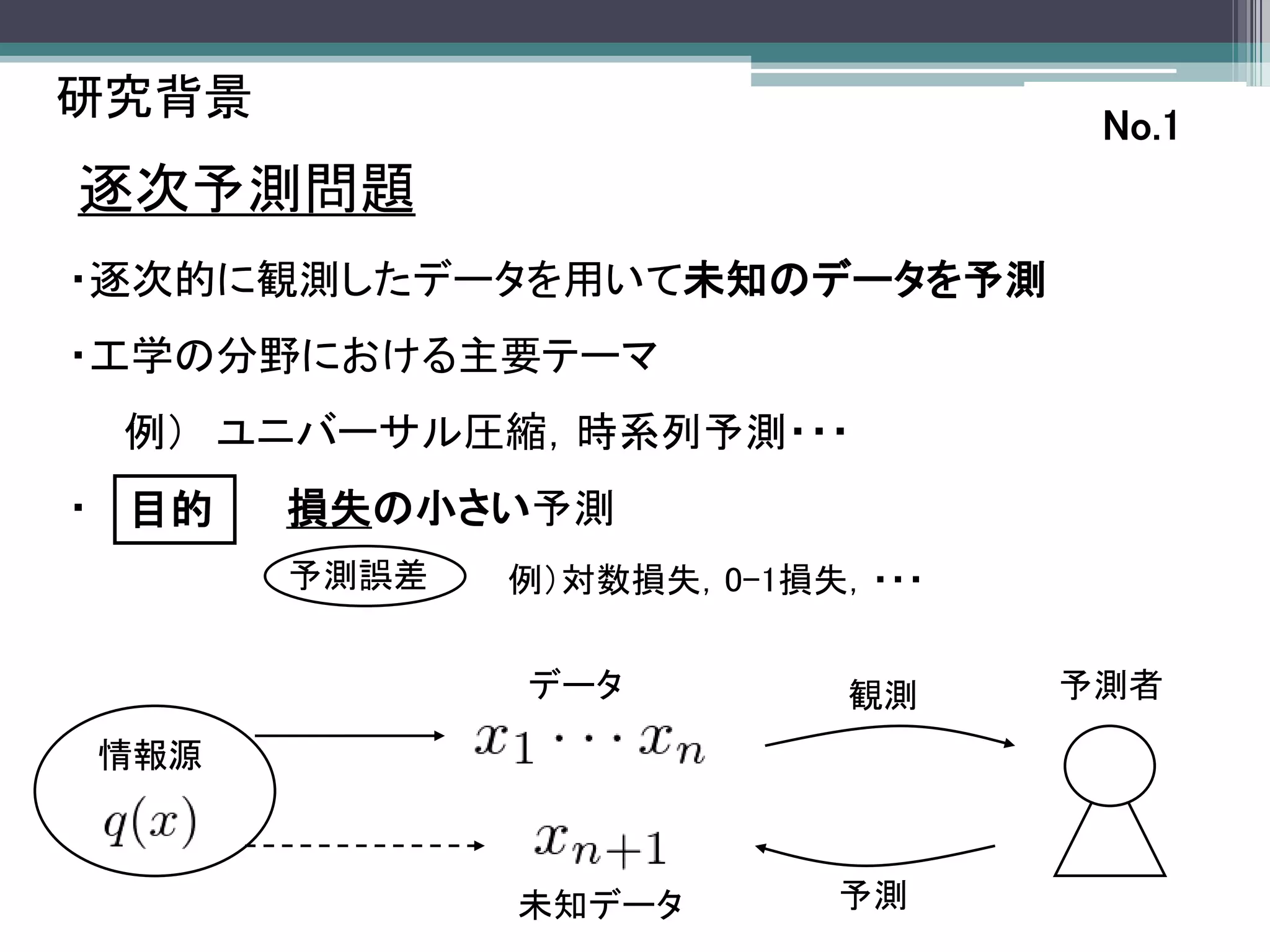
逐次予測問題
・逐次的に観測したデータを用いて未知のデータを予測
・工学の分野における主要テーマ
例） ユニバーサル圧縮，時系列予測・・・
・ 目的 損失の小さい予測
予測誤差 例）対数損失，0-1損失，・・・
データ 観測 予測者
情報源
未知データ 予測

3. 研究目的 No.2
従来研究の整理と本研究の目的
・損失関数の分類 ・・・ 1時点の対数損失と累積対数損失
・ベイズ基準の下での予測 ・・・ 真のモデルとモデル族の関係
モデル族は真のモデルを モデル族は真のモデルを
含む 含まない
1時点の対数損失 [Watanabe,2010] [Watanabe,2010]
累積対数損失 [Clarke&Barron,1990] 本研究
・ベイズ基準の下での予測における累積対数損失
本研究の に対するリスクの漸近評価
目的
・モデル族は実際には真のモデルを含まない

4. 問題設定 (1 / 5)
No.3
逐次予測問題の問題設定
・仮定 ：データ（連続値），
：真のモデル
は に従ってi.i.d.で発生
・既知 ：ある時点までの観測データ
・未知
問題 を用いて を予測
： を得た下での の予測値

5. 問題設定 (2 / 5) No.4
評価基準
・1時点の対数損失
・累積対数損失
・リスク関数 ユニバーサル圧縮に
おける冗長度と等価
は未知
損失関数，リスク関数の最小化は不可能

6. 問題設定 (3 / 5)
No.5
ベイズ基準の下での予測
・予測の際に以下を仮定
：（パラメトリック）モデル族
： 次元パラメータ空間
未知パラメータ
：パラメータの事前分布
・ を仮定 ・・・ を で表現可能
損失関数 ・・・
リスク関数 ・・・
・評価基準 ・・・ ベイズリスク関数

7. 問題設定 (4 / 5) No.6
ベイズ基準の下での予測 （続き）
・ベイズ最適な予測 ・・・ ベイズリスク関数を最小とする予測
ただし， ：事後分布
・ベイズ最適な予測における累積対数損失
ただし，

8. 問題設定 (5 / 5) No.7
ベイズ基準の下での予測 （続き）
・ の仮定 ・・・ ベイズ最適な予測の導出
・しかし は未知 ・・・ 必ずしも とは限らない
本研究では以下の状況・・・
・予測者は と仮定して（考えて）ベイズ最適な予測
・しかし，実際には

9. 従来研究 (1 / 4) No.8
Clarke&Barronの従来研究(1990)
・ の漸近評価 真のパラメータ
・ ・・・
条件 i)． は の内部に唯1つ存在， はコンパクト
ii)． は2階連続微分可能，各導関数は有界
iii)． は連続，
iv)． は正定値行列
v)．事後分布 の への一致性
： 次正方行列

10. 従来研究 (2 / 4) No.9
Clarke&Barronの主結果
定理[Clarke&Barron,1990]
パラメータの次元
定数
：フィッシャー情報行列

11. 従来研究 (3 / 4) No.10
証明の概要
の近傍の点を中心とした展開
・ に対して の近傍の点 を中心にラプラス近似
は の近傍

12. 従来研究 (4 / 4) No.11
証明の概要 （続き）
・ を利用
・主要項以外の誤差項は漸近的に0に収束

13. 本研究 (1 / 6) No.12
・ の漸近評価
・ ・・・ は存在しない
と の
カルバックライブラー
情報量
を考える
条件 i)． は の内部に唯1つ存在， はコンパクト
ii)． は3階連続微分可能，各導関数は有界
iii)． は2階連続微分可能，
iv)． は正則行列
は最尤推定量

14. 本研究 (2 / 6) No.13
本研究の主結果
定理
定数
定数
と の
カルバックライブラー
情報量

15. 本研究 (3 / 6)
No.14
証明の概要
最尤推定量 を中心とした展開
・ に対して を中心にラプラス近似
・ の漸近正規性（ の周りで）
補題[White,1982]
i)．
正規分布
ii)．
iii)．
iv)． は正定値行列

16. 本研究 (4 / 6) No.15
証明の概要 （続き）
① ②
の周りで の漸近正規性 カルバックライ
ラプラス近似 （ の周りで） ブラー情報量

17. 本研究 (5 / 6) No.16
証明の概要 （続き）
① に対して を中心にラプラス近似
は の近傍
補題i)，ii) ＋ 有界収束定理

18. 本研究 (6 / 6)
No.17
証明の概要 （続き）
② を の周りでテーラー展開
＋ 補題ii) ＋ 有界収束定理
漸近分布の
補題iii) の漸近正規性
共分散行列

19. 考察 (1 / 3) No.18
・ の場合
・ の場合
部について
の場合 ・・・
の場合 ・・・
と が一致しない分の差が となって出現

20. 考察 (2 / 3) No.19
・ の場合
・ の場合
部について
の場合 ・・・
の場合 ・・・

21. 考察 (3 / 3) No.20
マルコフモデルへの拡張
Clarke&Barronと本研究の結果はマルコフモデルへ拡張可能
例） 真のモデルが3次のマルコフモデル
仮定したモデル族が・・・
3次のマルコフモデル
・モデル族が真のモデルを含む
・Clarke&Barronの結果を適用
2次以下のマルコフモデル，またはi.i.d.モデル
・モデル族が真のモデルを含まない
・本研究の結果を適用

22. まとめ No.21
逐次予測問題に対して
モデル族が真のモデルを含まない状況で
ベイズ最適な予測を行った場合の
累積対数損失に対するリスクの漸近評価を行った

23. 付録 (1 / 2) No.22
Clarke&Barronの証明の補足
・ラプラス近似について
i)． を の周りでテーラー展開
ii)． は
を利用（ガウス積分）
は 次正方行列

24. 付録 (2 / 2) No.23
本研究の証明の補足
・ラプラス近似について
を の周りでテーラー展開
・有界収束定理（ルベーグの収束定理）
確率変数 が有界で ならば
や を として使用