Downloaded 220 times
![参考文献
• [1] 岡谷貴之, 斉藤真樹. ディープラーニング チュートリアル.
http://www.vision.is.tohoku.ac.jp/index.php/download_file/view/15/137/
• [2] Andrew Ng. CS294A Lecture notes: Sparse autoencoder.
http://www.stanford.edu/class/cs294a/sparseAutoencoder.pdf
• [3] 得居誠也. Deep Learning 技術の今.
https://www.slideshare.net/beam2d/deep-learning20140130](https://image.slidesharecdn.com/autoencoder20140526up-140524232630-phpapp02/85/NN-2014-5-26-2-320.jpg)
![プレトレーニング
• 深い多層NNの誤差逆伝搬法による学習はランダムな初
期値ではあまりうまくいかない (2.1.2節)
• よい初期値を与えるために、事前に層毎の教師無し学習
を行う (pretraining)
• あらためてネットワーク全体を学習する (fine-tuning)
[1]より
pretraining fine-tuning](https://image.slidesharecdn.com/autoencoder20140526up-140524232630-phpapp02/85/NN-2014-5-26-4-320.jpg)
![オートエンコーダの性質
• 入力を復元できるhを得る
– → 学習サンプルの構造を低次元で (bottleneck) or ス
パースに (スパース正則化) 捉える変換を学習してい
る
• オートエンコーダを自然画像から切り出したパッチで学
習した結果:
[2]より](https://image.slidesharecdn.com/autoencoder20140526up-140524232630-phpapp02/85/NN-2014-5-26-8-320.jpg)
![オートエンコーダによるプレトレーニング
• 入力層からの2層に、仮想的にデコーダを乗せて学習
• hを入力と見なして、次の2層を同様に学習
• 繰り返し
[1]より](https://image.slidesharecdn.com/autoencoder20140526up-140524232630-phpapp02/85/NN-2014-5-26-9-320.jpg)
![オートエンコーダの微調整 (fine tuning)
• 微調整 (fine tuning): プレトレーニング後に、ネットワー
ク全体を学習し直して最終的なモデルを得る
• 教師無し、有りともによい初期値が与えられているので
うまく学習できる (よい局所解にたどり着ける)
教師有り
各ノードがクラス
ラベルに対応する
出力層を乗せて、
(BPで)学習
教師無し
全体をひとつのオー
トエンコーダとみな
して学習
[1]より](https://image.slidesharecdn.com/autoencoder20140526up-140524232630-phpapp02/85/NN-2014-5-26-10-320.jpg)
![スパースオートエンコーダ
• Wではなくhをスパースにすることに注意
– Wを基底の集合としてみると、できるだけ少数の基底
の組み合わせで入力を再現できるように学習
• スパースコーディングと似ている
[1]より](https://image.slidesharecdn.com/autoencoder20140526up-140524232630-phpapp02/85/NN-2014-5-26-12-320.jpg)
![スパースコーディング
スパースコ ード = [0, 0, …, 0, 0.8, 0, …, 0, 0.3, 0, …, 0, 0.5, …]
Figs from [Yu and Ng, Feature learning for im age classification, Tutorial, ECCV10]
Olshausen, Field, Sparse Coding w ith an Overcom plete Basis Set: a Strategy Em ployed by V1?, Vis. Research96
0.8 * + 0.3 * + 0.5 *
Natural im age patches
min
,
1
2
+
過完備性
（ overcom plete）
{ } = , … ,](https://image.slidesharecdn.com/autoencoder20140526up-140524232630-phpapp02/85/NN-2014-5-26-14-320.jpg)
![[論文紹介] Convolutional Neural Network(CNN)による超解像](https://cdn.slidesharecdn.com/ss_thumbnails/cnn-presen-161218113749-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]SoftTriple Loss: Deep Metric Learning Without Triplet Sampling (ICCV2019)](https://cdn.slidesharecdn.com/ss_thumbnails/yokota20190920dlhack-190920011134-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Set Transformer: A Framework for Attention-based Permutation-Invariant...](https://cdn.slidesharecdn.com/ss_thumbnails/20200221settransformer-200221020423-thumbnail.jpg?width=640&height=640&fit=bounds)
多層NNの教師なし学習 コンピュータビジョン勉強会＠関東 2014/5/26
- 1.
- 2. 参考文献 • [1] 岡谷貴之,斉藤真樹. ディープラーニング チュートリアル. http://www.vision.is.tohoku.ac.jp/index.php/download_file/view/15/137/ • [2] Andrew Ng. CS294A Lecture notes: Sparse autoencoder. http://www.stanford.edu/class/cs294a/sparseAutoencoder.pdf • [3] 得居誠也. Deep Learning 技術の今. https://www.slideshare.net/beam2d/deep-learning20140130
- 3. はじめに • オートエンコーダによるプレトレーニングが主な話題 • 深いNNに対して、事前の学習でよい初期値を与えるこ とでよい局所解を得られるようにする手法 •深いNNの学習を可能にしたブレークスルーのひとつだ が、最近ではプレトレーニングは不要というのがトレン ド？
- 4. プレトレーニング • 深い多層NNの誤差逆伝搬法による学習はランダムな初 期値ではあまりうまくいかない (2.1.2節) •よい初期値を与えるために、事前に層毎の教師無し学習 を行う (pretraining) • あらためてネットワーク全体を学習する (fine-tuning) [1]より pretraining fine-tuning
- 5. プレトレーニング • 層毎の教師無し学習の方法 – DeepBelief Network (DBN) の場合 • → RBMをContrastive Divergence法で学習 (4節) – 多層NNの場合 • → オートエンコーダ
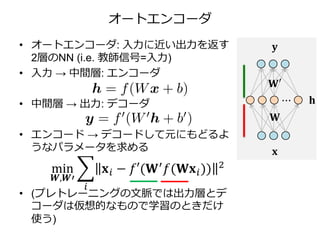
- 6. オートエンコーダ • オートエンコーダ: 入力に近い出力を返す 2層のNN(i.e. 教師信号=入力) • 入力 → 中間層: エンコーダ • 中間層 → 出力: デコーダ • エンコード → デコードして元にもどるよ うなパラメータを求める • (プレトレーニングの文脈では出力層とデ コーダは仮想的なもので学習のときだけ 使う)
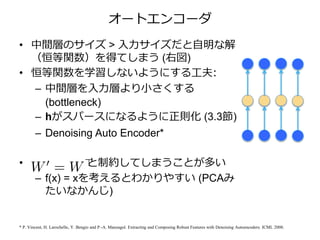
- 7. オートエンコーダ • 中間層のサイズ >入力サイズだと自明な解 （恒等関数）を得てしまう (右図) • 恒等関数を学習しないようにする工夫: – 中間層を入力層より小さくする (bottleneck) – hがスパースになるように正則化 (3.3節) – Denoising Auto Encoder* • と制約してしまうことが多い – f(x) = xを考えるとわかりやすい (PCAみ たいなかんじ) * P. Vincent, H. Larochelle, Y. Bengio and P.-A. Manzagol. Extracting and Composing Robust Features with Denoising Autoencoders. ICML 2008.
- 8. オートエンコーダの性質 • 入力を復元できるhを得る – →学習サンプルの構造を低次元で (bottleneck) or ス パースに (スパース正則化) 捉える変換を学習してい る • オートエンコーダを自然画像から切り出したパッチで学 習した結果: [2]より
- 9.
- 10. オートエンコーダの微調整 (fine tuning) •微調整 (fine tuning): プレトレーニング後に、ネットワー ク全体を学習し直して最終的なモデルを得る • 教師無し、有りともによい初期値が与えられているので うまく学習できる (よい局所解にたどり着ける) 教師有り 各ノードがクラス ラベルに対応する 出力層を乗せて、 (BPで)学習 教師無し 全体をひとつのオー トエンコーダとみな して学習 [1]より
- 11. スパースオートエンコーダ • 中間層を搾ることでトリビアルな解を避けられるが、特 徴を表現する能力は制限される • 代わりにhがなるべくスパースになるという制約を入れ て学習する •最も単純なのは • g(･)は など 正則化項
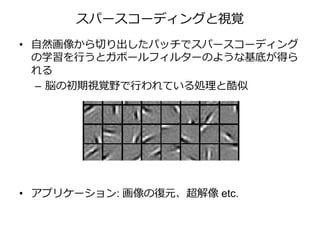
- 12. スパースオートエンコーダ • Wではなくhをスパースにすることに注意 – Wを基底の集合としてみると、できるだけ少数の基底 の組み合わせで入力を再現できるように学習 •スパースコーディングと似ている [1]より
- 13. スパースコーディング* • 与えられたサンプルを少数の基底の線形結合で表現でき るように、基底の集合(dictionary)を学習 • 学習時にはD,hを最適化、Dがきまればxに対してhを計 算 • 基底の数 > 特徴次元: overcomplete * Olshausen, B. A. and Field, D. J.: Emeregnce of simple- cell receptive field properties by learning a sparse code for natural images, Nature, Vol. 381, pp. 607– 609 (1996). スパースコ ーディ ング , Sparse Coding w ith an Overcom plete Basis Set: a Strategy Em ployed by V1?, Vis. R min , 1 2 + 過 （ { } = , … , dictionary code スパース項: 理想的にはL0
- 14. スパースコーディング スパースコ ード =[0, 0, …, 0, 0.8, 0, …, 0, 0.3, 0, …, 0, 0.5, …] Figs from [Yu and Ng, Feature learning for im age classification, Tutorial, ECCV10] Olshausen, Field, Sparse Coding w ith an Overcom plete Basis Set: a Strategy Em ployed by V1?, Vis. Research96 0.8 * + 0.3 * + 0.5 * Natural im age patches min , 1 2 + 過完備性 （ overcom plete） { } = , … ,
- 15. スパースコーディングと視覚 • 自然画像から切り出したパッチでスパースコーディング の学習を行うとガボールフィルターのような基底が得ら れる – 脳の初期視覚野で行われている処理と酷似 •アプリケーション: 画像の復元、超解像 etc. 1 2 + 過完 （ ove = , … ,
- 16. スパースオートエンコーダとスパースコーディング • スパースオートエンコーダ: • スパースコーディング •オートエンコーダは陽に存在するエンコーダにより、h を求める • スパースコーディングでは最適化の過程で陰にエンコー ドされる
- 17. Topographic ICA • スパースコーディング、オートエンコーダでは基底の順 序には意味がない –生物の視覚野では捉える特徴の分布が物理的な距離 に対応している (近い細胞?は似た特徴に反応) • プーリングとの組み合わせにより回転等への不変 性を実現 • TICAはこうした性質を学習により獲得しようというも の http://www.mathworks.com/matlabcentral/fileexchange/23253-gabor-filterより
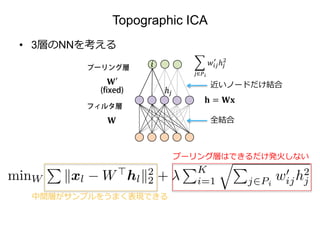
- 18. 不変性 • 不変性: 入力パターンにいろいろな変形を加えて入力し たとき、ノードの反応が変わらない •例えば、CNN + max-poolingは (小さな) 並進への不変性 がある • 不変性を持った処理を積み重ねていくことで、低次の見 えの変化に関わらず、より高次の概念に反応するノード を学習するのがDeep Learningがやっていること?
- 19.
- 20. Topographic ICA • プーリング層の発火を抑えるには、 同じプーリングユニットにつながっているフィルタ層の ノードは似たパターンに反応するべき – 常に少数のユニットが反応をするより、たまに多数 のユニットが反応する方が上の値は小さくなる • 結果同じプーリングユニットには似た特徴がつながる – → プーリングユニットが微笑な変形に不変性を持つ
- 21. まとめ • 事前の教師無し学習(プレトレーニング)によって、学習 が難しい多層NNにより初期値を与えることが出来る • 教師無し学習は、入力をできるだけ再現できる中間表現 への変換を求めることで行う •オートエンコーダの学習では、制約無しだとトリビアル な解になってしまうので制約を入れる • スパース制約を入れたオートエンコーダは、スパース コーディングに酷似 • TICAはさらに特徴の不変性を考慮した学習方法