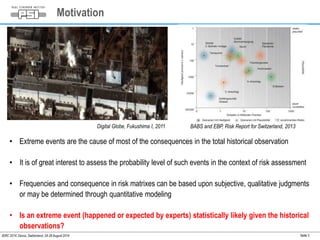
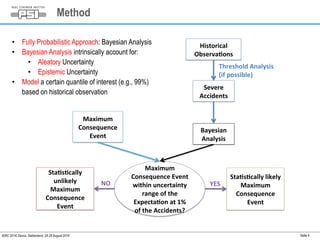
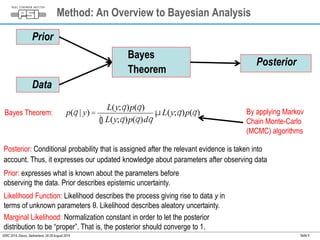
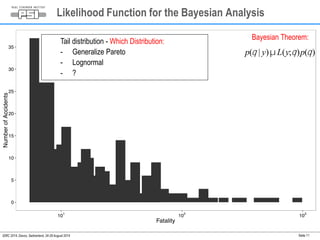
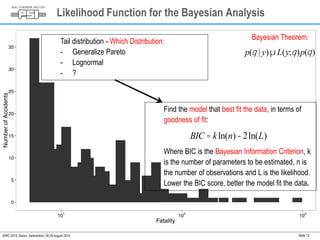
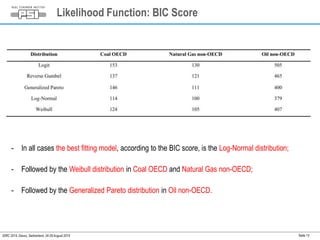
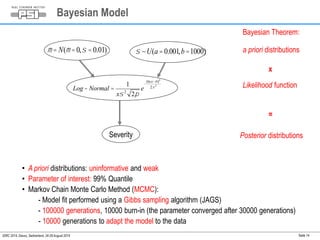
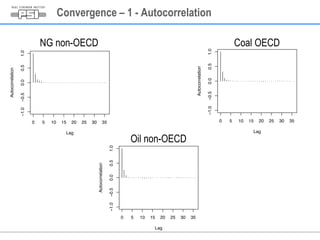
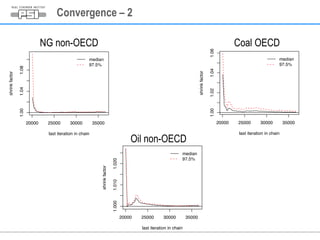
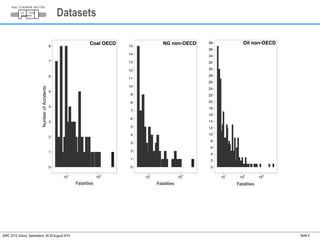
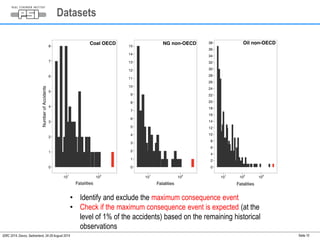
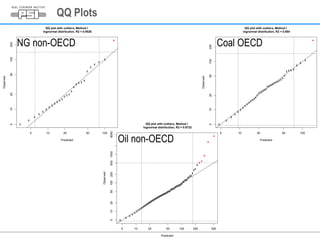
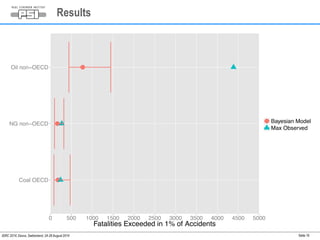
This document summarizes a study on assessing the probability of extreme consequence accidents in the energy sector based on historical observations. The study uses a Bayesian analysis approach on accident data from the ENSAD database. Key findings include: 1) A log-normal distribution best fits the accident severity data for most energy types and regions. 2) Extreme accidents were found to be statistically expected at a 1% probability level for coal in OECD and natural gas in non-OECD countries. 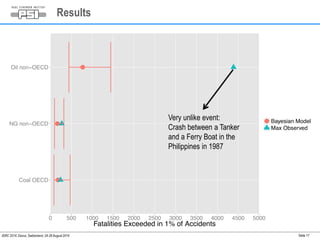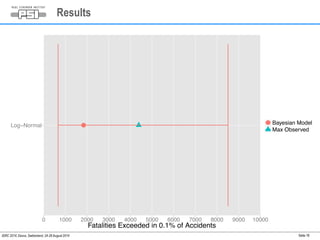3) One extreme oil accident in non-OECD countries was found to be statistically unlikely given historical data.

1. Wir schaffen Wissen – heute für morgen
Paul Scherrer Institut
Matteo Spada and Peter Burgherr
Towards Extreme Consequence Accidents in Energy
Sector: Are they expected based on historical
observations?
IDRC 2014, Davos, Switzerland, 24-28 August 2014

2. • Motivation
• Method
• Application to the Energy Sector:
• ENSAD database
• Likelihood Function
• Bayesian Model
• Results
• Conclusions
Outline
IDRC 2014, Davos, Switzerland, 24-28 August 2014 Seite 2

3. Motivation
Digital Globe, Fukushima I, 2011 BABS and EBP, Risk Report for Switzerland, 2013
• Extreme events are the cause of most of the consequences in the total historical observation
• It is of great interest to assess the probability level of such events in the context of risk assessment
• Frequencies and consequence in risk matrixes can be based upon subjective, qualitative judgments
or may be determined through quantitative modeling
• Is an extreme event (happened or expected by experts) statistically likely given the historical
observations?
IDRC 2014, Davos, Switzerland, 24-28 August 2014 Seite 3

4. Method
Historical
Observa ons
Threshold Analysis
(if possible)
Severe
Accidents
Bayesian
Analysis
• Fully Probabilistic Approach: Bayesian Analysis
• Bayesian Analysis intrinsically account for:
• Aleatory Uncertainty
• Epistemic Uncertainty
• Model a certain quantile of interest (e.g., 99%)
based on historical observation
Maximum
Consequence
Event
Maximum
Consequence Event
within uncertainty
NO YES
range of the
Expecta on at 1%
of the Accidents?
Sta s cally likely
Maximum
Consequence
Event
Sta s cally
unlikely
Maximum
Consequence
Event
IDRC 2014, Davos, Switzerland, 24-28 August 2014 Seite 4

5. μL(y;q )p(q ) By applying Markov
Chain Monte-Carlo
(MCMC) algorithms
Seite 5
Method: An Overview to Bayesian Analysis
Prior
Bayes
Theorem
Posterior
Data
Bayes Theorem:
p(q | y) =
L(y;q )p(q )
ò L(y;q )p(q )dq
Posterior: Conditional probability that is assigned after the relevant evidence is taken into
account. Thus, it expresses our updated knowledge about parameters after observing data
Prior: expresses what is known about the parameters before
observing the data. Prior describes epistemic uncertainty.
Likelihood Function: Likelihood describes the process giving rise to data y in
terms of unknown parameters θ. Likelihood describes aleatory uncertainty.
Marginal Likelihood: Normalization constant in order to let the posterior
distribution to be “proper”. That is, the posterior should converge to 1.
IDRC 2014, Davos, Switzerland, 24-28 August 2014

6. Coal mine explosion Deepwater Horizon (US)
LNG facility (Algeria)
Gas Refinery pipeline Tapped oil pipeline (Nigeria)
Seite 6
Test the Method: Accidents in the Energy Sector
IDRC 2014, Davos, Switzerland, 24-28 August 2014

7. ENSAD database
Seite 7
ENergy related Severe Accident Database (ENSAD)
- Comprehensive, worldwide coverage of energy-related severe accidents, 1970-2008 covered
- Covers entire energy chains (the risk to society and environment occur not only during the actual
energy generation)
- Updated from a variety of sources
Coal (incl. Lignite)
Exploration
Mining & Preparation
Transport
Conversion
Transport
Power/Heating Plant
Waste Treatment & Disposal
Natural Gas
Exploration
Extraction & Processing
Transport
Power/Heating Plant
Oil
Exploration
Extraction
Transport
Refining
Transport
Power/Heating Plant
Waste Treatment & Disposal
IDRC 2014, Davos, Switzerland, 24-28 August 2014

8. ENSAD database
Seite 8
ENergy related Severe Accident Database (ENSAD)
- Comprehensive, worldwide coverage of energy-related severe accidents, 1970-2008 covered
- Covers entire energy chains (the risk to society and environment occur not only during the actual
energy generation)
- Updated from a variety of sources
- ENSAD definition of severe accidents: ≥5 fatalities, ≥10 injured, ≥5 Mio $, etc.
Risk description Impact Category ENSAD severity threshold Consequence indicator
Human health Fatalities
Injuries
≥ 5
≥ 10
Fatalities per GWeyr
Injured per GWeyr
Societal Evacuees
Food consumption ban
≥ 200
yes
Evacuees per GWeyr
Nominal scale
Environmental Release of hydrocarbons
Land/water contamination
≥ 10’000 t
≥ 25 km2
Ton per GWeyr
km2 per GWeyr
Economic Economic loss ≥ 5 Mio USD (2000) USD per GWeyr
IDRC 2014, Davos, Switzerland, 24-28 August 2014

9. Datasets
IDRC 2014, Davos, Switzerland, 24-28 August 2014 Seite 9

10. Datasets
Seite 10
• Identify and exclude the maximum consequence event
• Check if the maximum consequence event is expected (at the
level of 1% of the accidents) based on the remaining historical
observations
IDRC 2014, Davos, Switzerland, 24-28 August 2014

11. Likelihood Function for the Bayesian Analysis
Bayesian Theorem:
Seite 11
Tail distribution - Which Distribution:
- Generalize Pareto
- Lognormal
- ?
IDRC 2014, Davos, Switzerland, 24-28 August 2014
p(q | y)μL(y;q )p(q )

12. Likelihood Function for the Bayesian Analysis
Bayesian Theorem:
Find the model that best fit the data, in terms of
goodness of fit:
Where BIC is the Bayesian Information Criterion, k
is the number of parameters to be estimated, n is
the number of observations and L is the likelihood.
Lower the BIC score, better the model fit the data.
Seite 12
Tail distribution - Which Distribution:
- Generalize Pareto
- Lognormal
- ?
BIC = k ln(n)-2ln(L)
IDRC 2014, Davos, Switzerland, 24-28 August 2014
p(q | y)μL(y;q )p(q )

13. Seite 13
Likelihood Function: BIC Score
- In all cases the best fitting model, according to the BIC score, is the Log-Normal distribution;
- Followed by the Weibull distribution in Coal OECD and Natural Gas non-OECD;
- Followed by the Generalized Pareto distribution in Oil non-OECD.
IDRC 2014, Davos, Switzerland, 24-28 August 2014

14. Bayesian Model
Bayesian Theorem:
Seite 14
m = N(m = 0,s = 0.01) s ~U(a = 0.001,b =1000)
Log - Normal =
1
xs 2 2p
Severity
e
-
(ln x-m )2
2s 2
• A priori distributions: uninformative and weak
• Parameter of interest: 99% Quantile
• Markov Chain Monte Carlo Method (MCMC):
x
=
- Model fit performed using a Gibbs sampling algorithm (JAGS)
- 100000 generations, 10000 burn-in (the parameter converged after 30000 generations)
- 10000 generations to adapt the model to the data
IDRC 2014, Davos, Switzerland, 24-28 August 2014
a priori distributions
Likelihood function
Posterior distributions

15. Results
Seite 15
• Fatalities exceeded in 1% of Accidents. Maximum observed consequences not inside the
uncertainty range at this probability level are considered as not expected based on the historical
data.
• Results are shown for the following country groups:
• Oil non-OECD
• Natural Gas non-OECD
• Coal OECD
• All results include uncertainty level: 5% - 95%
IDRC 2014, Davos, Switzerland, 24-28 August 2014

16. Results
IDRC 2014, Davos, Switzerland, 24-28 August 2014 Seite 16

17. Results
Very unlike event:
Crash between a Tanker
and a Ferry Boat in the
Philippines in 1987
IDRC 2014, Davos, Switzerland, 24-28 August 2014 Seite 17

18. Results
IDRC 2014, Davos, Switzerland, 24-28 August 2014 Seite 18

19. Conclusions
• Fully Probabilistic approach, which counts for both aleatory and epistemic uncertainty, is defined in
order to test the expectation of a given catastrophic event with respect to the historical information
• The methodology could be used to prove the expectation of an event based on expert judgement,
commonly used in risk assessment analysis
• For the energy sector, with respect to the historical observation:
• Coal OECD and Natural Gas non-OECD extreme events are expected at 1% of the accidents
• Oil non-OECD extreme event is not expected at 1% of the accidents
• Oil non-OECD extreme event is expected at 0.1% of the accidents
IDRC 2014, Davos, Switzerland, 24-28 August 2014 Seite 19

20. Thank You! Questions?
matteo.spada@psi.ch
www.psi.ch/ta/mspada
IDRC 2014, Davos, Switzerland, 24-28 August 2014 Seite 20

21. Seite 21
Backup Slides

22. QQ Plots
5 10 20 50 100
5 10 20 50 100 200
QQ plot with outliers, Method I
lognormal distribution, R2 = 0.9526
Predicted
Observed
NG non-OECD
5 10 20 50 100
5 10 20 50 100 200
QQ plot with outliers, Method I
lognormal distribution, R2 = 0.984
Predicted
Observed
Coal OECD
5 10 20 50 100 200 500
5 10 20 50 100 200 500 1000 5000
QQ plot with outliers, Method I
lognormal distribution, R2 = 0.9722
Predicted
Observed
Oil non-OECD

23. Marginal Likelihood: MCMC with Gibbs Sampler
• The Gibbs sampler is a generic method to sample from a high dimensional distribution.
• Consider two parameters of interest: θ1 and θ2
• Target: p(θ1, θ2 | y)
• Suppose we can sample from p(θ1 | θ2,y) and p(θ2 |θ1,y).
• Starting at the point (θ1(0) , θ2(0)) in parameter space, generate a random walk, a sequence (θ1(k),
θ2(k)) as follows:
For k=1,...,n, define θ1(k) ~p(θ1 | θ2(k-1),y), θ2(k) ~ p (θ2 | θ1( k ) , y )
• The values at the (k+1)th step depend only on the values at the k-th step and are independent of
previous values.
• The Markov chain will in general tend to a stationary distribution, and the stationary distribution will be
the desired p(θ1, θ2 | y)

24. Convergence – 1 - Autocorrelation
NG non-OECD Coal OECD
Oil non-OECD

25. Convergence – 2
NG non-OECD Coal OECD
Oil non-OECD