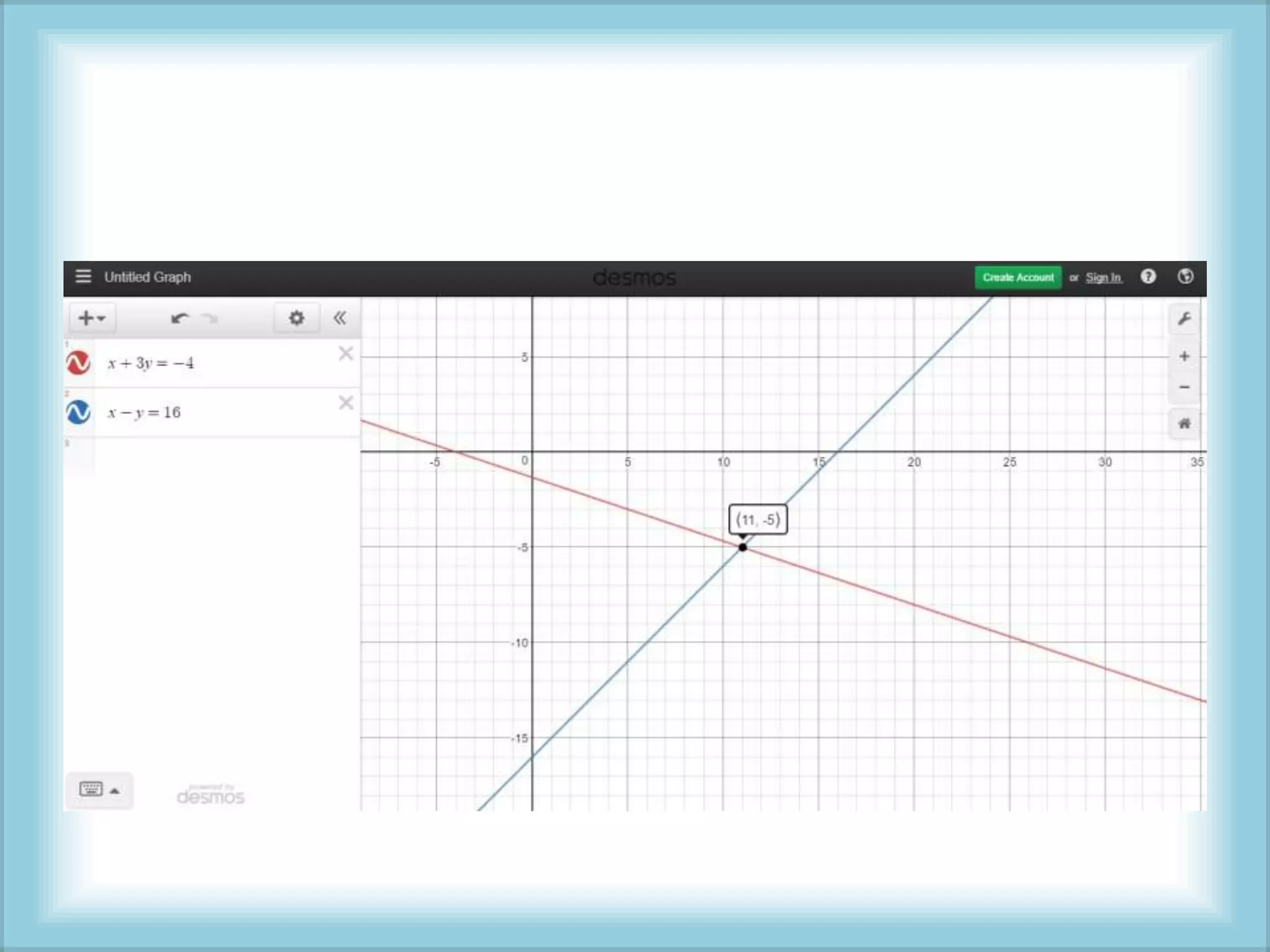
This document describes the substitution method for solving systems of linear equations in two variables. It involves solving one equation for one of the variables and substituting that expression into the other equation to find the value of the other variable. The example shows solving the system of equations x + 3y = -4 and x - y = 16 by first solving the first equation for x in terms of y, then substituting that expression into the second equation to solve for y, and finally substituting the value of y back into the original expression for x to find the solution set (-11, -5).

1. SOLVING SYSTEMS OF
LINEAR EQUATION IN TWO
VARIABLES
(SUBSTITUTION METHOD)

2. SYSTEMS OF LINEAR EQUATION
• Two or more linear equations.
• A SOLUTION to a system of linear
equations in two variables consists of
an ordered pair that satisfies both
equations.

3. SUBSTITUTION METHOD
• Solve for one of the variables in one
of the equations and then substitute
that variable in the other equation.

4. Example:
𝒙 + 𝟑𝒚 = −𝟒 Equation 1
𝒙 − 𝒚 = 𝟏𝟔Equation 2
STEP 1: Solve one of the equations either "x= “ or "𝒚 = “.
Using Equation 1, find the value of x.
𝒙 + 𝟑𝒚 = −𝟒
− 𝟑𝒚 = −𝟑𝒚
𝒙 = −𝟑𝒚 − 𝟒(partial
value of x)

5. STEP 2: Substitute the expression into
the other equation.
Note: We used Equation 1 to get
Substitute the partial value of 𝒙to Equation 2to
find the value of 𝒚.
𝒙 − 𝒚 = 𝟏𝟔Equation 2
−𝟑𝒚 − 𝟒 − 𝑦 = 16
−𝟑𝒚 − 4 − 𝒚 = 16
−𝟒𝒚 − 4 = 16
𝟒 = 𝟒
−𝟒𝒚
−𝟒
=
𝟐𝟎
−𝟒
𝒙 = −𝟑𝒚 −
𝟒(partial value of
x)
𝒚 = −𝟓
(value of y)

6. STEP 3: Using the expression obtained
in step 1, SUBSTITUTE the value of the
variable obtained in step 2.
• NOTE: In Step 1, we get
and in Step 2, we found that
𝒙 = −𝟑𝒚 − 𝟒
= −𝟑 −𝟓 − 𝟒
= 𝟏𝟓 − 𝟒
𝒙 = −𝟏𝟏
So, the solution set is (−𝟏𝟏, −𝟓).
𝒙 = −𝟑𝒚 − 𝟒(partial
value of x)
𝒚 = −𝟓
(value of y)